DOI: 10.11817/j.issn.1672-7207.2018.12.018

京沪铁路钢桁拱桥温差特性的长期监测与分析

王高新¹，丁幼亮²

(1. 中国矿业大学 深部岩土力学与地下工程国家重点实验室，江苏 徐州，221008；

2. 东南大学 混凝土及预应力混凝土结构教育部重点实验室，江苏 南京，210096)

摘要：基于大胜关长江大桥温度场的长期监测数据，考察边桁拱整体竖向温差、杆构件横截面温差和桥面构件横向温差的空间分布特征，利用统计学方法对这3类主要温差的正温差和负温差样本分别进行概率统计特征分析，确定其Weibull概率密度函数的参数估计值。参照欧洲规范计算出这3类主要温差的正温差和负温差标准值，并通过温差样本相关性和归类对比分析，最终得到这3类主要温差的最不利温差分布模式。研究结果表明：边桁拱整体竖向温差以及杆件截面温差明显，在结构计算时应予以考虑；正负温差的概率统计特征均可以采用Weibull概率密度函数来较好地描述；整体竖向温差存在3种最不利温差模式，杆件截面温差各存在2种最不利温差模式。研究成果可为钢桁拱桥结构形式的温差效应计算提供参考和依据。

关键词：钢桁拱桥；温差；空间分布特性；概率统计特性；标准值

中图分类号：U448.3             文献标志码：A         文章编号：1672-7207(2018)12-3040-11

Long-term monitoring and analysis of characteristics of temperature difference in steel truss arch bridge of Beijing—Shanghai railway

WANG Gaoxin¹, DING Youliang²

(1. State Key Laboratory for Geomechanics and Deep Underground Engineering,China University of Mining and Technology, Xuzhou 221008, China;

2. The Key Laboratory of Concrete and Prestressed Concrete Structures of Ministry of Education,Southeast University, Nanjing 210096, China)

Abstract: With the long-term monitoring data of temperature field from the Dashengguan Yangtze Bridge, the spatial distribution characteristics of integral vertical temperature differences from lateral truss arch, cross section temperature differences from bar members and transverse temperature differences from bridge deck members were investigated, and then the probability statistic characteristics of positive and negative temperature difference samples from the lateral truss arch and bar members were analyzed to acquire the estimated parameter values of Weibull distribution. Standard values of positive and negative temperature differences were calculated for continuous steel truss arch girder. Furthermore, the most adverse temperature difference models were obtained for integral vertical temperature differences of lateral truss arch, cross section temperature differences of bar members and transverse temperature differences of bridge deck members, by means of correlation analysis of temperature difference samples, classification and comparison. The results show that the side arch truss contains big vertical temperature gradients and the truss members contain big cross-sectional temperature gradients, which should be taken into consideration during structural calculation; The probability statistics feature of positive and negative temperature gradients can be well described by one Weibull probability density function; The vertical gradients in the whole truss contain three adverse temperature difference patterns, and the cross-sectional temperature gradients between truss members contain two adverse temperature patterns. The research results can provide reference for effect calculation of temperature difference from continuous steel truss arch bridge.

Key words: steel truss arch bridge; temperature difference; spatial distribution characteristics; probability statistic characteristics; standard value

大跨度桥梁结构受到四季交替的温度作用会产生较大的温度自应力以及附加应力，从而导致结构构件在服役期内出现较大变形、开裂以及动力特性变异等^[1-6]，因此，温度作用是影响大跨桥梁结构使用寿命的重要因素之一^[7-10]。为此，国内外桥梁研究者已针对混凝土箱形梁形式和扁平钢箱梁形式的温差特性进行研究，例如，叶见曙等^[11-12]对南京长江二桥北汊桥的混凝土箱梁温度场进行了3 d(仅白天)的现场观测，发现箱梁顶板上边缘最大温差为20 ℃，且向下至腹板按指数函数分布；雷笑等^[13]对一座具有100 mm沥青铺装层的预应力混凝土梁桥箱梁进行了为期2 a的温度观测和统计分析，得到混凝土箱梁的最大温差标准值为17.3 ℃；丁幼亮等^[14]对润扬大桥北汊斜拉桥的扁平钢箱梁温度场进行为期1 a的长期监测，得到扁平钢箱梁的顶板横向温差特性；王高新等^[15]基于润扬大桥北汊斜拉桥扁平钢箱梁的温度监测数据，进行了顶板与底板横向温差的统计特性研究，得到扁平钢箱梁顶板横向温差标准值的最大绝对值为13.8 ℃。然而目前主要研究对象仅局限于混凝土箱形梁形式和扁平钢箱梁形式，而对于钢桁拱桥结构形式的温差特性研究甚少。虽然钢桁梁桥为穿透式结构，但由于钢桁拱桥结构形式复杂，杆件种类众多，结构和杆件尺寸超大，且受到阳面背面以及白天、夜晚、四季交替的温度作用影响，导致温度场分布也复杂多变且存在温差影响，目前研究尚未明确指出钢桁拱桥结构形式的温差分布特性及概率统计特征等，且无法得知可用于钢桁拱桥温度效应计算的温差分布模式，因此开展钢桁拱桥结构形式的温差特性分析工作具有重要意义。本文作者基于京沪高铁大胜关长江大桥温度场的长期监测数据，首先利用极值分析方法详细考察了边桁拱整体竖向温差、杆构件(上弦杆、下弦杆、桥面杆和斜腹杆)横截面温差和桥面构件(钢桥面板和加劲梁)横向温差的空间分布特征，然后利用统计学方法对边桁拱整体竖向温差和杆构件横截面温差的正温差和负温差样本分别进行概率统计特征分析，在此基础上参照欧洲规范计算出边桁拱整体竖向温差、杆构件横截面温差和桥面构件横向温差具有五十年一遇的正温差和负温差标准值，并进一步结合温差样本相关性分析和归类对比给出边桁拱整体竖向温差、杆构件横截面温差和桥面构件横向温差的最不利温差模式，从而为钢桁拱桥的温度效应计算提供参考和依据。

1  钢桁拱桥监测断面及传感器布置

大胜关长江大桥是京沪高速铁路和沪汉蓉铁路共用的跨江通道，桥梁同时搭载南京市的双线地铁，上部结构为(108+192+336+336+192+108) m的钢桁拱桥，其中主跨336 m的设计尺寸名列世界同类高速铁路桥梁之首。大胜关长江大桥的立面图如图1所示，其钢桁拱桥如图2所示，是由3片主桁拱、桁间支撑、钢桥面板和横向加劲梁组成，其中主桁拱又由上弦杆、下弦杆、桥面弦杆、斜腹杆和竖腹杆组成，桁间支撑又由水平支撑和竖向支撑组成。选取图1所示的1-1截面作为监测断面并布置温度传感器W₁~W₁₂如图2(a)所示，其中W₁~W₈沿高度方向依次布置于钢桁拱桥边桁拱两侧，其在2-2剖面、3-3剖面、4-4剖面、5-5剖面和6-6剖面的具体位置分别如图2(b)~2(f)所示，W₉与W₁₀，W₁₁与W₁₂分别沿横向布置于钢桁拱桥的钢桥面板和横向加劲梁上，W_i表示第i个温度传感器(i=1，…，12)，采样频率为1 Hz。

图1  大胜关长江大桥立面图(单位：m)

Fig. 1  Vertical view of Dashengguan Yangtze River

图2  钢桁拱桥监测断面及温度传感器布置(单位：mm)

Fig. 2  Monitoring sections and locations of temperature sensors in steel truss arch bridge

2  钢拱桁桥温差的空间分布特征

环境温度和结构温度具有相似的“夏季温度高、冬季温度低”的季节变化特征和近似单周期正弦曲线的日变化特征^[14-18]，从2013-03-01—10-30的温度监测结果中筛选出230 d具有正弦曲线变化形式的典型温度样本，每个温度传感器W_i对应的典型温度样本记为t_i。进一步分析，由于相邻10 min内的温度变化不大^[16]，可利用10 min内的温度平均值来代表此时段的所有温度，每天可得到144个温度平均值，因此230 d内每个典型温度样本t_i共得到33 120个温度。在此基础上，将2个典型温度样本t_i和t_j在同一时刻的温度相减，便得到典型温差样本t_i,j，i，j=1，2，…，12，且i≠j。钢桁拱桥杆件的最大温差一般出现在上午10时或下午16时，最小温差一般出现在夜晚21时至凌晨6时^[18]，其中白天温差较大是因为受到日照阳面和日照阴面影响，夜晚温差较小是因为钢桁拱桥杆件在夜间不再受到日照辐射而且热传递作用使得温度场趋于均匀。根据温度传感器W_i在钢桁拱桥上的布置特点，将钢桁拱桥温差的空间分布特征划分为以下3类：1) 边桁拱整体竖向温差分布特征；2) 杆构件横截面温差分布特征；3) 桥面构件横向温差分布特征。

2.1  边桁拱整体竖向温差分布特征

选用位于不同高度处的上弦杆、下弦杆和桥面弦杆之间竖向温差来描述边桁拱整体竖向温差分布特征。由于3个弦杆在上游侧和下游侧各存在一个典型温度样本，因此对每个弦杆采用上下游两侧的温度平均值来代表此弦杆的整体温度变化，并将不同弦杆之间整体温度相减，便得到上弦杆与下弦杆之间、上弦杆与桥面弦杆之间、下弦杆与桥面弦杆之间的竖向温差样本t_ud，t_ub和t_db的变化曲线分别如图3所示。从图3可以看出：3个温差样本均存在一定正温差和负温差，其中下弦杆与桥面弦杆之间的竖向正温差可达到8.6 ℃，因此在温差效应计算时应考虑边桁拱整体竖向温差的影响。

图3  竖向温差样本t_ud，t_ub和t_db的变化曲线

Fig. 3  Changing curves of vertical temperature differences t_ud, t_ub and t_db

2.2  杆构件横截面温差分布特征

采用上弦杆、下弦杆和桥面弦杆箱型横截面的典型温差样本t_1,2，t_5,6，t_7,8和斜腹杆工字型横截面的典型温差样本t_3,4来描述钢桁拱杆构件的温差分布特征，其变化曲线分别如图4所示。从图4可以看出：对于弦杆构件，上弦杆横截面的正温差和负温差最为明显，可分别达到9.6 ℃和-14.7 ℃；下弦杆次之，其横截面的正温差和负温差可分别达到6.4 ℃和-11.2 ℃；桥面弦杆横截面温差主要以正温差为主，且最大正温差可达到5.3 ℃；斜腹杆横截面存在一定正温差和负温差，最大值分别达到6.5 ℃和-7.8 ℃。因此在温差效应计算时应考虑杆构件横截面温差的影响。

2.3  桥面构件横向温差分布特征

采用钢桥面板横向典型温差样本t_9,10和加劲梁横向典型温差样本t_11,12来描述桥面横向温差的分布特征，其变化曲线分别如图5所示。从图5可以看出：钢桥面板和加劲梁横向正温差和负温差均很小，因此在温差效应计算时可不予考虑。

图4  杆构件温差样本t_1,2，t_3,4，t_5,6和t_7,8的变化曲线

Fig. 4  Changing curves of temperature differences t_1,2, t_3,4, t_5,6 and t_{7,8 in truss members}

图5  桥面横向温差样本t_9,10和t_11,12的变化曲线

Fig. 5  Changing curves of transverse temperature differences t_9,10 and t_{11,12 in bridge deck}

3  钢桁拱桥温差概率统计特征

3.1  钢桁拱桥温差概率统计方法

温差样本t_i,j的时程变化是一个同分布的平稳随机过程，根据平稳随机过程的遍历性定理，可以将其视为一个随机变量，并运用非线性最小二乘估计得到其概率密度函数^[16]。由于正温差和负温差在钢桁拱桥中产生的温度应力会有明显差别，因此将钢桁拱桥温差样本t_i,j按正温差和负温差分别考虑，从t_i,j中筛选出日正温差极值样本和日负温差极值样本^[17]。通过对多种概率密度函数的拟合优度比较，钢桁拱桥和的概率密度统计特性最终选用一个Weibull概率密度函数来描述，其计算公式分别如下：

         (1)

       (2)

式中：；和分别表示和的概率密度函数；a和b分别为Weibull分布函数的尺度参数和形状参数。需要指出的是，由于Weibull分布函数在负值区域内不存在，因此需要先将取相反数变为正值(即=)，再利用Weibull分布函拟合其概率密度。由于桥面构件横向温差很小，因此主要对边桁拱整体竖向温差和杆构件横截面温差进行概率统计特征分析。

3.2  边桁拱整体竖向温差概率统计特征

考察边桁拱上弦杆与下弦杆之间、上弦杆与桥面弦杆之间、下弦杆与桥面弦杆之间的竖向温差样本t_ud，t_ub和t_db的概率统计特征。以t_ud为例对其概率统计特征进行分析，首先从t_ud中筛选出日正温差极值样本和日负温差极值样本，然后对日负温差极值样本取相反数变为正值，然后利用统计学方法分别对和进行概率密度统计，得到其概率密度柱状图如图6所示，在此基础上分别利用式(1)和式(2)对和的概率密度进行最小二乘拟合，得到拟合曲线及其参数估计值如图6所示。基于以上分析方法，图7和图8所示分别为和，和的概率密度柱状图及其拟合曲线和参数估计值。从图7和图8可以看出拟合曲线能够较好地反映边桁拱实测竖向温差的概率密度统计特性，进一步对每个概率密度函数拟合优度进行5%显著性水平上的Kolmogorov-Smirnov检验，检验结果均使实测概率密度服从拟合函数的原假设成立，说明每个概率密度函数具有良好的拟合优度。

图6  和的概率密度柱状图及其拟合曲线

Fig. 6  Probability density histograms of , and their fitting curves

图7  和的概率密度柱状图及其拟合曲线

Fig. 7  Probability density histograms of , and their fitting curves

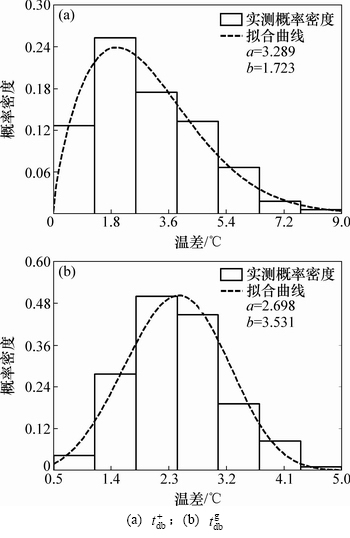
图8  和的概率密度柱状图及其拟合曲线

Fig. 8  Probability density histograms of , and their fitting curves

3.3  杆构件横截面温差概率统计特征

考察边桁拱弦杆箱型横截面典型温差样本t_1,2，t_5,6，t_7,8和边桁拱斜腹杆工字型横截面典型温差样本t_3,4的概率统计特征。参照边桁拱整体竖向温差概率统计特征的分析方法，首先计算各个杆件截面的日正负温差极值样本的概率统计特征，然后再利用Weibull概率密度函数对概率密度统计特征进行最小二乘拟合，最终得到所有杆构件典型温差样本的概率密度柱状图及其拟合曲线和参数估计值分别如图9~12所示。从图9~12可以看出：拟合曲线能够较好地反映杆构件横截面实测温差的概率密度统计特性。为了定量评价Weibull概率密度函数的拟合效果，进一步对每个概率密度函数拟合优度进行5%显著性水平上的Kolmogorov-Smirnov检验，结果表明每个概率密度函数的拟合优度均通过检验。说明采用Weibull概率密度函数可以较好地反映概率密度统计特性。

图9  和的概率密度柱状图及其拟合曲线

Fig. 9  Probability density histograms of , and their fitting curves

图10  和的概率密度柱状图及其拟合曲线

Fig. 10  Probability density histograms of , and their fitting curves

图11  和的概率密度柱状图及其拟合曲线

Fig. 11  Probability density histograms of , and their fitting curves

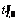图12  和的概率密度柱状图及其拟合曲线

Fig. 12  Probability density histograms of , 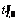and their fitting curves

4  钢桁拱桥温差标准值及温差模式

4.1  钢桁拱桥温差标准值

我国TB 10002.1—2005“铁路桥涵设计基本规范”将温度(均匀温度和梯度温度)作用视为附加力，但并未进一步明确说明温度标准值的计算方法^[19]，故本文研究参照欧洲结构设计标准I的规定，即温度标准值是具有50 a重现期的温度作用值。按照我国铁路桥梁设计规范中的100 a设计基准期计算，最大温度作用超过温度标准值次数的数学期望为2次。因此，和对应的温差标准值和分别采用如下公式计算^[13]：

        (3)

      (4)

式中：P为超越概率；和分别为和的概率密度函数；和分别为和的样本容量。上述方法同样适用于t_ud，t_ub和t_db的温差标准值计算。基于以上分析方法，并结合前述钢桁拱桥温差的概率密度统计特征分析，计算得到边桁拱整体竖向温差标准值及杆构件横截面温差标准值如表1所示。从表1可以看出：上弦杆和下弦杆横截面的温差标准值很明显。此外，由于桥面横向温差很小，因此其温差标准值为0 ℃。

表1中的钢桁拱桥温差标准值与其实测温差极值存在一一对应关系，例如上弦杆横截面温差样本t_1,2的负温差标准值为-20.6 ℃，其对应的负温差极值为-14.7 ℃(由图4(a)得到)，因此绘制钢桁拱桥温差标准值与实测温差极值之间的相关性散点图如图13所示。从图13可以看出：两者之间具有良好的线性相关特性，进一步利用最小二乘法对此线性相关特性进行拟合，得到拟合函数表达式为：t_y=1.482t_x+1.144，其中t_y为温差标准值，t_x为实测温差极值。此函数表达式揭示了钢桁拱桥温差标准值与实测温差极值之间的内在规律。

4.2  钢拱桁桥温差模式

为计算温度作用对钢桁拱桥结构效应的影响，需要已知最不利温差模式。基于以上钢桁拱桥温差标准值计算结果并结合温差样本互相关分析，研究钢桁拱桥的3类温差模式，即边桁拱整体竖向温差模式、杆构件横截面温差模式和桥面构件横向温差模式。

表1  钢桁拱桥温差标准值

Table 1  Standard values of temperature difference in steel truss arch bridge

图13  温差标准值与实测温差极值之间的互相关性散点图

Fig. 13  Correlation scatter plots between standard values of temperature difference and monitoring extreme values of temperature difference

4.2.1  边桁拱整体竖向温差模式

边桁拱整体竖向温差可由3种工况，即t_ud和t_ub，t_ud和t_db以及t_ub和t_db来确定，每种工况又同时存在正温差和正温差、正温差和负温差、负温差和正温差、负温差和负温差这4种组合，因此边桁拱整体竖向温差共存在12种竖向温差模式。这12种竖向温差模式中的某些模式之间可能存在相互排斥，可通过相关性分析对相互排斥的模式筛选，获取有效的边桁拱整体竖向温差模式。

1) t_ud和t_ub的相关性分析。绘制t_ud和t_ub之间的相关性散点图如图14所示。从图14可以看出：当t_ud逐渐增大时，t_ub并未明显表现出逐渐增大或减小的趋势。因此当t_ud取正温差标准值时，t_ub可能取正温差标准值，也可能取负温差标准值；当t_ud取负温差标准值时，t_ub可能取正温差标准值，也可能取负温差标准值，即存在以下4种温差模式：

第1种温差模式：t_u-t_d=7.1 ℃，t_u-t_b=8.2 ℃；

第2种温差模式：t_u-t_d=7.1 ℃，t_u-t_b=-5.7 ℃；

第3种温差模式：t_u-t_d=-5.5 ℃，t_u-t_b=8.2 ℃；

第4种温差模式：t_u-t_d=-5.5 ℃，t_u-t_b=-5.7 ℃。

2) t_ud和t_db的相关性分析。绘制t_ud和t_db之间的相关性散点图如图15所示。从图15可以看出t_ud和t_ub之间存在较好的负相关特性，即t_db随t_ud的逐渐增大而减小。因此当t_ud取正温差标准值时，t_ub只存在取负温差标准值的情况；当t_ud取负温差标准值时，t_ub只存在取正温差标准值的情况，即存在以下2种温差模式：

第5种温差模式：t_u-t_d=7.1 ℃，t_d-t_b=-5.0 ℃；

第6种温差模式：t_u-t_d=-5.5 ℃，t_d-t_b=11.6 ℃。

3) t_ub和t_db的相关性分析。绘制t_ub和t_db之间的相关性散点图如图16所示。从图16可以看出：t_ub和t_db之间具有明显的正相关特性，即t_db随t_ud的逐渐增大而增大。因此当t_ub取正温差标准值时，t_db只存在取正温差标准值的情况；当t_ub取负温差标准值时，t_db只存在取负温差标准值的情况，即存在2种以下温差模式：

图14  t_ud和t_ub之间的互相关性散点图

Fig. 14  Correlation scatter plots between t_ud and t_ub

图15  t_ud和t_db之间的互相关性散点图

Fig. 15  Correlation scatter plots between t_ud and t_db

图16  t_ub和t_db之间的互相关性散点图

Fig. 16  Correlation scatter plots between t_ub and t_db

第7种温差模式：t_u-t_b=8.2 ℃，t_d-t_b=11.6 ℃；

第8种温差模式：t_u-t_b=-5.7 ℃，t_d-t_b=-5.0 ℃。

基于以上对12种温差模式进行相关性分析，剔除了4种不可能出现的温差模式。若以桥面弦杆温度T_b作为基准点(即令t_b=0 ℃)，则剩余8种温差模式取值如表2所示，进一步将此8种温差模式归类并对比不同温差模式t_u与t_d之间、t_u与t_b之间和t_d与t_b之间的温差绝对值，便可确定最不利温差模式：① 第3种、第6种和第7种温差模式同属于“t_u＜t_d＞t_b”类型，将其归为一类并相互对比可知第3种温差模式为此类型最不利温差模式；② 第2种和第5种温差模式同属于“t_u＞t_d＜t_b”类型，将其归为一类并相互对比可知：第2种温差模式为最不利温差模式；③ 第4种和第8种温差模式同属于“t_u＜t_d＜t_b”类型，由于其t_u和t_b取值与第2种温差模式相同，对比此3种温差模式可知第2种温差模式为最不利温差模式；④ 第1种温差模式单独归为“t_u＞t_d＞t_b”类型，由于其t_u和t_b取值与第3温差模式相同，对比这2种温差模式发现均为最不利温差模式。基于以上分析，得到边桁拱整体竖向温差的3种最不利温差模式分别为：

第1种最不利温差模式：t_u=8.2 ℃，t_d=1.1 ℃，t_b= 0 ℃；

第2种最不利温差模式：t_u=-5.7 ℃，t_d=-12.8 ℃，t_b=0 ℃；

第3种最不利温差模式：t_u=8.2 ℃，t_d=13.7 ℃，t_b=0 ℃。

5.2.2  杆构件横截面温差模式

基于杆构件横截面温差标准值计算结果，可直接得到上弦杆横截面的2种最不利温差模式为：t₁-t₂=16.3 ℃，t₁-t₂=-20.6 ℃；下弦杆横截面的2种最不利温差模式为：t₅-t₆=15.8 ℃，t₅-t₆=-16.7 ℃；桥面弦杆横截面的2种最不利温差模式为：t₇-t₈=7.8 ℃，t₇-t₈=-2.1 ℃；斜腹杆横截面的2种最不利温差模式为：t₃-t₄=10.9 ℃，t₃-t₄=-8.3 ℃。

5.2.3  桥面构件横向温差模式

由于钢桥面板和加劲梁横向正温差和负温差标准值均为0 ℃，因此其最不利温差模式分别为：t₉-t₁₀= 0 ℃，t₁₁-t₁₂=0 ℃。

表2  8种温差模式取值

Table 2  Values of 8 kinds of temperature difference patterns

5  结论

1) 类似于混凝土箱梁和扁平钢箱梁存在的较大温差，边桁拱整体竖向温差、上弦杆、下弦杆和桥面弦杆箱型横截面温差、斜腹杆工字型横截面温差也较为明显，在进行温差效应计算时应予以考虑；钢桥面板横向温差和加劲梁横向温差很小，在温差效应计算时可不予考虑。

2) 边桁拱整体竖向温差、上弦杆、下弦杆和桥面弦杆箱型横截面温差、斜腹杆工字型横截面温差的正负温差样本的概率统计特征均可以采用一个Weibull概率密度函数来较好地描述，并给出了各正负温差样本的概率密度参数估计值。

3) 钢桁拱桥温差标准值与实测温差极值具有良好的线性相关特性，边桁拱整体竖向温差存在3种最不利温差模式，上弦杆、下弦杆、桥面弦杆和斜腹杆各存在2种最不利温差模式，钢桥面板和加劲梁仅承受均匀温度作用。

参考文献：

[1] 邓扬, 李爱群, 丁幼亮. 大跨悬索桥梁端位移与温度的相关性研究及其应用[J]. 公路交通科技, 2009, 26(5): 54-58.

DENG Yang, LI Aiqun, DING Youliang. Research and application of correlation between beam end displacement and temperature of long span suspension bridge[J]. Journal of Highway and Transportation Research and Development, 2009, 26(5): 54-58.

[2] GUO Tong, LI Aiqun, LI Jianhui. Fatigue life prediction of welded joints in orthotropic steel decks considering temperature effect and increasing traffic flow[J]. Structural Health Monitoring, 2008, 7(3):189-202.

[3] 卢志芳, 刘沭宇, 李倩. 考虑温度和湿度变化的钢-混组合连续梁桥徐变效应分析[J]. 中南大学学报(自然科学版), 2015, 46(7): 2650-2657.

LU Zhifang, LIU Shuyu, LI Qian. Creep effect analysis of steel-concrete composite bridge considering mutative temperature and relative humidity[J]. Journal of Central South University(Science and Technology), 2015, 46(7): 2650-2657.

[4] GUO Tong, LI Aiqun, WANG Hao. Influence of ambient temperature on the fatigue damage of welded bridge decks[J]. International Journal of Fatigue, 2008, 30(6): 1092-1102.

[5] 李嘉, 赵乾文, 邵旭东. 全无缝化桥梁接线路面温升效应及端部位移计算[J]. 中南大学学报(自然科学版), 2016, 47(10): 3538-3545.

LI Jia, ZHAO Qianwen, SHAO Xudong. Research on temperature effect and anchor deformation for approach pavement of jointless bridge[J]. Journal of Central South University(Science and Technology), 2017, 48(9): 3538-3545.

[6] BARSOTTI R, FROLI M. Statistical analysis of thermal actions on a concrete segmental box-girder bridge[J]. Structural Engineering International, 2000, 10(2): 111-116.

[7] 林鸣, 付宏渊, 颜东煌. 考虑温度与时变因素耦合的混凝土桥梁增量分析方法[J]. 中南大学学报(自然科学版), 2017, 48(9): 2506-2512.

LIN Ming, FU Hongyuan, YAN Donghuang. Incremental analysis considering coupling temperature and time-dependent effects of concrete bridge[J]. Journal of Central South University(Science and Technology), 2017, 48(9): 2506-2512.

[8] KIM A S, PARK S, WU J, et al. Temperature variation in steel box girders of cable-stayed bridges during construction[J]. Journal of Constructional Steel Research, 2015, 112: 80-92.

[9] LIU Wenshuo, DAI Gonglian, RAO Shaochen. Numerical calculation on solar temperature field of a cable-stayed bridge with U-shaped section on high-speed railway[J]. Journal of Central South University, 2014, 21(8): 3345-3352.

[10] LOU Ping, ZHU Junpu, DAI Gonglian, et al. Experimental study on bridge–track system temperature actions for Chinese high-speed railway[J]. Archives of Civil and Mechanical Engineering 2018, 18(2): 451-464.

[11] 叶见曙, 贾琳, 钱培舒. 混凝土箱梁温度分布观测与研究[J]. 东南大学学报(自然科学版), 2002, 32(15): 69-74.

YE Jianshu, JIA Lin, QIAN Peishu. Observation and research on temperature distribution in concrete box girders[J]. Journal of Southeast University (Natural Science Edition), 2002, 32(15): 69-74.

[12] 叶见曙, 雷笑, 王毅. 基于统计分析的混凝土箱梁温差标准值研究[J]. 公路交通科技, 2009, 26(11): 50-54.

YE Jianshu, LEI Xiao, WANG Yi. Study of characteristic value of thermal difference of concrete box girder based on statistical analysis[J]. Journal of Highway and Transportation Research and Development, 2009, 26(11): 50-54.

[13] 雷笑, 叶见曙, 王毅. 日照作用下混凝土箱梁的温差代表值[J]. 东南大学学报(自然科学版), 2008, 38(6): 1105-1109.

LEI Xiao, YE Jianshu, WANG Yi. Representative value of solar thermal difference effect on pc box-girder[J]. Journal of Southeast University(Natural Science Edition), 2008, 38(6): 1105-1109.

[14] 丁幼亮, 王高新, 周广东, 等. 基于现场监测数据的润扬大桥斜拉桥钢箱梁温度场全寿命模拟方法[J]. 土木工程学报, 2013, 46(5): 129-136.

DING Youliang, WANG Gaoxin, ZHOU Guangdong, et al. Life-cycle simulation method of temperature field of steel box girder for Runyang cable-stayed bridge based on field monitoring data[J]. China Civil Engineering Journal, 2013, 46(5): 129-136.

[15] 王高新, 丁幼亮, 李爱群, 等. 基于长期监测数据的润扬大桥斜拉桥钢箱梁横向温差特性研究[J]. 工程力学, 2013, 30(1): 163-167.

WANG Gaoxin, DING Youliang, LI Aiqun, et al. Characteristics of transverse temperature differences of steel box girder in Runyang cable-stayed bridge using long-term monitoring[J]. Engineering Mechanics, 2013, 30(1): 163-167.

[16] 周广东, 丁幼亮, 李爱群, 等. 基于长期实测数据的大跨悬索桥扁平钢箱梁温差特性研究[J]. 土木工程学报, 2012, 45(5): 114-125.

ZHOU Guangdong, DING Youliang, LI Aiqun, et al. Thermal difference characteristic analysis of a flat steel box girder in long-span suspension bridge based on long-term field measurement data[J]. China Civil Engineering Journal, 2012, 45(5): 114-125.

[17] DING Youliang, WANG Gaoxin. Estimating extreme temperature differences in steel box girder using long-term measurement data[J]. Journal of Central South University, 2013, 20(9): 2537-2545.

[18] WANG Gaoxin, DING Youliang. Research on monitoring temperature difference from cross sections of steel truss arch girder of Dashengguan Yangtze Bridge[J]. International Journal of Steel Structures, 2015, 15(3): 647-660.

[19] TB 10002.1—2005, 铁路桥涵设计基本规范[S].

TB 10002.1—2005, Fundamental code for design on railway and culvert[S].

(编辑  赵俊)

收稿日期：2018-01-10；修回日期：2018-04-16

基金项目(Foundation item)：国家重点基础研究计划项目(2015CB060000)；国家自然科学基金资助项目(51578138)；中国博士后科学基金资助项目(2017M621865)；中央高校基本科研业务费专项资金资助项目(JB180068)(Project(2015CB060000) supported by National Key Basic Research Program; Project(51578138) supported by the National Natural Science Foundation of China; Project(2017M621865) supported by the China Postdoctoral Science Foundation; Project(JB180068) supported by Fundamental Research Funds for the Central Universities)

通信作者：丁幼亮，博士，研究员，博士生导师，从事桥梁健康监测研究；E-mail：civilchina@hotmail.com