J. Cent. South Univ. (2016) 23: 10-17

DOI: 10.1007/s11771-016-3043-y

Analysis of 13Cr bloom solidification structure using CA-FE model

ZHAI Ying-ying(翟莹莹)¹, MA Bei-yue(马北越)¹, LI Ying(厉英)¹, JIANG Zheng-yi(姜正义)²

1. School of Materials and Metallurgy, Northeastern University, Shenyang 110819, China;

2. School of Mechanical, Materials and Mechatronic Engineering, University of Wollongong,Wollongong 2522, Australia

Central South University Press and Springer-Verlag Berlin Heidelberg 2016

Abstract: Solidification structure is critical in the control of the mechanical properties and quality during the continuous casting process. the thermo-physical properties of 13Cr steel added some rare metals, such as Mo, V, Nb, are measured to better understand the solidification structure of 13Cr bloom. A computational model using CA-FE (cellular automation-finite element) method coupled with heat transfer model is developed to describe the solidification structure in continuous casting process. It is found that the calculated solidification structure is in good agreement with the observed data. The influence of casting speed and superheat on the solidification structure of the bloom is studied in detail. In order to obtain more equiaxed crystal ratio and low degree of the segregation in the bloom, the optimized casting speed 0.6 m/min and superheat less than 25 °C are determined for the caster. Using the optimized manufacturing parameters, these samples are 60% with the equiaxed zone ratio of 8%–10% and below the degree of segregation 1.05.

Key words: cellular automation; solidification structure; equiaxed crystal ratio; bloom; continuous casting

1 Introduction

13Cr martensitic stainless steel displays high strength and toughness at low temperature, and has been mainly used as pipelines to transport oil and gas. Some rare metal elements are added to the steel to improve the corrosion resistance. During the continuous casting process, cracks, porosity, segregation and other quality defects can be easily generated [1]. To solve the segregation problem, to reduce columnar grain structure and to obtain the desired solidification structure of 13Cr bloom added with rare metal elements, it is necessary to simulate the solidification structure to get the optimum technological parameters.

Numerical simulation is an economic and desirable method in the study of continuous casting process to understand the solidification phenomena of steel [2-5]. Dendritic microstructures are favourable for improving the final properties of components manufactured from them. The dendrites can be part of either a columnar or equiaxed grain structure depending on the local thermal and solutal fields. Columnar dendrites often grow near the mould surface when the thermal gradients are high, transforming to an equiaxed microstructure. They are conditioned on when the gradient is reduced in the centre of the casting process. Several models have been proposed to predict the solidification structure including stochastic models [6-7] and deterministic models [8]. The common dendrite growth formation is based on dendrite tip growth kinetics model [9-10].

In this work, the main goal is to build a simulation model of solidification structure during continuous casting process including heat transfer simulation and micro simulation (heterogeneous nucleation, dendrite growth and solute diffusion). The CA-FE method is used to simulate the solidification structure of 13Cr added with rare metals taking into account the bulk liquid flow in the liquid core, considering various technological parameters in continuous casting process. The equiaxed and columnar dendrite are simulated as typical structures. The effect of casting speed and superheat on the casting solidification structure is analyzed. The optimum casting speed and superheat temperatures are given to obtain the maximum equiaxed crystal ratio. And the solidification structure is also investigated in the best casting speed and superheat ranges.

2 Thermo-physical properties

The basic chemical compositions of 13Cr steel added some rare metals are tested and listed in Table 1.The physical properties related to simulation of the solidification structure such as density, specific heat, thermal conductivity and thermal diffusivity are calculated, as shown in Fig. 1. The liquid phase temperature measured by the differential scanning calorimeter (DSC) is 1510 °C, the solid phase temperature is 1463 °C and the solidification range of the alloy is 47 °C [11]. The phase transformation L→L+δ occurs in the largest exothermic range of 1509-1472 °C. The phase transformation L+δ→γ occurs between 1472 and 1463 °C [12]. To the rare metal elements, the compositional undercooling of liquid metal is very small and the total number of crystals is not much, and these small crystals easily develop into coarse columnar crystals.

3 Mathematical model

The final quality of the steel depends on the solidification structure of the bloom. A CA-FE method is used to solve the heat conduction during the casting process. these results coupled with the cellular rules to simulate the evolution of grain structure based on the microscopic physical mechanism of the structure and the rules of the local cellular establishment. Considering the solidification theory, the grain size depends on these aspects. First of all, the heterogeneous nucleation of grain is formed in the liquid phase. Then, the priority growth direction is in <100> crystal orientation in the solidification process for the cubic metals. At last, the Kurz-Giovanola-Trivedi (KGT) model is applied to calculating the growth kinetics of columnar and equiaxed dendrites.

3.1 Heat transfer model

Numerical simulation is the best way to explain the relationship between 13Cr solidification microstructure and technological parameters. In this work, an unsteady heat transfer model [13] based on the slice moving method is established to simulate the bloom solidification in continuous casting process. It is assumed that a slice moved from the meniscus to the air cooling zone at the casting speed. Then, the solidification process with the whole continuous casting process can be simulated by changing the boundary conditions. The governing equation is shown as

                     (1)

where ρ is the material density; c is the specific heat capacity; λ is thermal conductivity; T is the temperature; t is the time; Q is the term associated to internal heat generation due to phase change.

Table 1 Main chemical compositions of 13Cr steel (mass fraction, %)

Fig. 1 measured thermo-physical properties of 13Cr steel:

The initial condition is the molten steel temperature at meniscus:

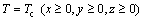                      (2)

The conditions of heat transfer with the surrounding medium are set at the boundary:

              (3)

During the bloom casting, the heat flux in different zones denotes as follows.

In the mould, the cooling water flow rate and the temperature at the inlet and outlet of the mould are known, so the average flux in the mould can be computed by

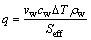                              (4)

where v_w is the water flow rate of the mould; c_w is the specific heat capacity of water; △T is the temperature difference between input and output water of mould; ρ_w is the water density; S_eff is the effective cooling area of mould; q is the heat flux.

In the secondary cooling zone, the cooling water flow rate is

      (5)

where s is Stefan-Boltzmann constant; ε is radiation coefficient; h is the heat transfer coefficient. T_w, T_a and T_b are the temperatures of cooling water, environment and strand surface, respectively. There are four segments in this zone, and h is different in every segment.

In the air cooling zone, the cooling water flow rate is

                (6)

In this section, the slice size is the same as the bloom of 425 mm×320 mm, and 10 mm in thickness. The computational domain of the 425 mm×320 mm×10 mm is divided into 42844 elements, as shown in Fig. 2.

Fig. 2 Grinding of computational domain

A fixed methodology is used with a heat source term due to phase transformation. The solid fraction depends on a number of parameters, but it is to assume f_s varying only with temperature, given by the following equation [14]:

                            (7)

where k₀ is the partition coefficient; T_L is the liquidus temperature; T_F is the solvent fusion temperature.

Solute diffusion equations in liquid and solid are shown in Eqs. (8) and (9), respectively.

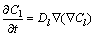                             (8)

                             (9)

The solute equilibrium at the solid-liquid interface is as below.

                                  (10)

where D_l and D_s are liquid diffusion and solid diffusion coefficients, respectively; k is the partition coefficient; 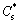 and  are solid concentration, liquid concentration at solid-liquid interface, respectively.

3.2 Heterogeneous nucleation model

Equiaxed solidification involves various phenomena that must be taken into account simultaneously. The aim of microscopic model is combining nucleation, grain growth and grain interaction in order to have a full description of equiaxed solidification. Cellular automata method is based on deterministic methods, nucleation and crystal growth kinetics theory for simulating the solidification process. Continuous nucleation model is applied to simulating the dendrites and eutectic [15]. In a certain supercooling degree, the nucleation density is the integral of Gaussian distribution, and nucleation characteristics should be a continuous curve rather than a discrete distribution. The model is described as

       (11)

where n is the nucleation density; n_max is the maximum nuclei density which can be reached when all the nucleation sites are activated during cooling; △T is the calculated local undercooling; △T_max is the mean undercooling; △T_s is the standard deviation.

3.3 Dendrite tip growth kinetics model

KGT model can simulate the growth kinetics of both columnar and equiaxed morphologies with different growth conditions [16]. Based on the marginal stability criterion, Eq. (12) can be obtained.

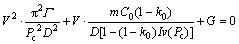      (12)

where V is the growth velocity at the dendrite tip; Γ is the Gibbs-Thomson coefficient, 1.9×10^{-7 in the simulation; m is the liquid slope; C}₀ is the initial alloy composition; P_c is the Peclet number for solute diffusion; D is the diffusion coefficient in liquid; k₀ is the partition coefficient; Iv(P_c) is the Ivantsov function; G is temperature gradient. Because G has little effect on the growth velocity of a dendrite tip, it can be regarded as 0.

The undercooling at a tip of dendrite, ΔT, is expressed as follows:

           (13)

where r is the dendrite tip radius, r=2D·P_c/V (D is the diffusion coefficient in liquid).

During the simulation process, KGT model is fitted and Eq. (14) is gained.

                         (14)

The heat transfer model is calculated by finite element method, and the grain growth process is simulated by CA method. Interpolation coefficients are defined between nodal points of FE grids and CA cells to combine the two methods in a single model to predict the grain growth as a function of the thermal field and influence of the latent heat release of the grains. This calculation method can realize the competition of crystal growth.

4 Results and discussions

The simulated temperature distributions and solidification shell thickness of 13Cr bloom in the casting speed 0.60 m/min and initial temperature    1529 °C are shown in Fig. 3. The cooling parameters used in this model are listed in Table 3. In order to simulate the solidification structure evolution of continuous casting steel and save calculation time, the cell size of 15 μm is adopted and each finite difference grid consists of 100×100 CA cells. Due to the axial symmetry of the heat transfer, a quarter of the cross section of strand was selected for the calculation domain. The equiaxed ratio is calculated by dividing the equiaxed zone area by the whole area. Given that the error range between the simulation results and the actual measurement temperature data is 0.3%-1.0%, the simulation is much accurate.

Table 2 Materials parameters of simulated 13Cr steel

Based on the materials parameters of Table 2 [17], the fitting coefficients in Eq. (14) a₂=1.84×10^{-6 m/(s-1}·k^-5), a₃=1.507×10^{-5 m/(s-1}·k^-3).

Table 3 Main characteristics of different cooling zones

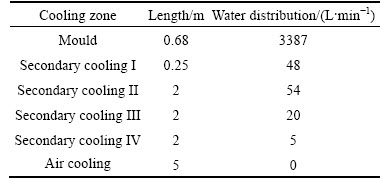
The effects of distance to meniscus on the simulated temperature and shell thickness are shown in Fig. 3. The temperature filed and shell thickness are calculated by Eq. (1) with the initial condition Eq. (2) and boundary condition Eq. (3). All the thermal physical properties shown in Fig. 1 are used to calculate the heat flux densities. In Fig. 3, the temperature reduces quickly because of the greatly cooling strength in the mould. The surface temperature reheats the joints of different cooling zones. The reheating speed is controlled lower than 100 °C/m. The temperature decreasing speed is lower than 150 °C/m. The shell thickness in the secondary cooling zone grows slowly because of the lower secondary cooling intensity compared to the mould. Due to the increasing solidified shell thickness, higher thermal resistance and reducing thermal conductivity, the temperature of straightening segment is between 940-1000 °C, avoiding the brittle zone 663-894 °C.

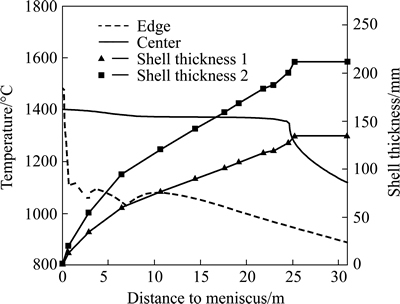
Fig. 3 Change curves of simulated temperature and shell thickness with distance to meniscus

The simulated temperatures are compared with the actual measured temperatures in Fig. 4 with the casting speed of 0.65 m/min and the superheat of 25 °C. Since the temperature is measured by infrared thermoscope, there exists 1% error in Fig. 4. The simulated temperature is in good agreement with the measured temperature with the error of 0.7%-1.5%.

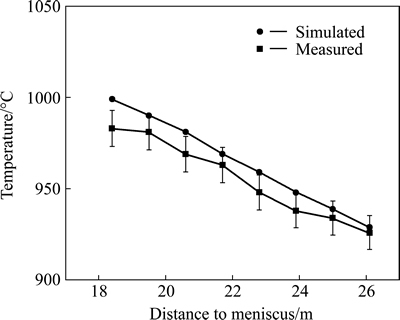
Fig. 4 Comparison of bloom surface temperature of simulation and experiment

The simulated solidification microstructure is compared with the tested result shown in Fig. 5. It can be seen that equiaxed crystal ratios of the simulated solidification and measured structure are 6.5% and 6.3%, respectively. The error is 0.2%, which demonstrates the simulation algorithm is acceptable. The simulated solidification structures agree well with the observed ones. There are three kinds of grain structures. chill zone is near the surface; equiaxed zone is formed in the center of the bloom; and columnar is between them. this model can be used to simulate the solidification structure since the nucleation parameters are reasonable. It is shown that when the columnar dendrite in the direction is perpendicular to the mould wall, the columnar dendrites will stop to grow, meeting at the diagonal. The equiaxed dendrites are formed at the center before the columnar dendrites reached the center, the columnar-to-equiaxed transition can occur.

Fig. 5 simulated

In Fig. 6, the macrostructure of 13Cr bloom in the continuously casting process with the 17 °C superheat. The equiaxed crystal ratio of simulation result is 8.6% and the equiaxed crystal ratio of the real bloom is 8.4% with the casting speed of 0.6 m/min. Figure 6 shows the organizational simulation photos with different drawing speeds. The equiaxed rates are 5.4%, 8.4%, 6.5%, 6.3% with casting speeds of 0.55, 0.60, 0.65, 0.70 m/min, respectively. Reducing the temperature gradient of the bloom has a major impact on casting solidification structure.

The influence of casting speed on the equiaxed crystal ratio is shown in Fig. 7. The equiaxed ratio increases and then decreases with the casting speed. The equiaxed crystal ratio is the maximum when the casting speed is 0.60 m/min. The shell thickness of the outlet of the mould becomes thin when the casting speed improves. The thermal capacity of shell enhances because the shell thickness becomes thin when the casting speed increases to a certain extent. The dendritic front temperature gradient caused by the thermal capacity is stronger than that caused by the secondary cooling effect. The equiaxed crystal ratio increases and then decreases with the casting speed.

Fig. 6 simulated solidification structures distribution at different casting speeds (△T=17 °C):

Fig. 7 Influence of casting speed on equiaxed crystal ratio

Figure 8 shows the simulation pictures of 13Cr solidification microstructure with different superheats. With the casting speed of 0.60 m/min, the equiaxed crystal ratios are 8.9%, 8%, 6.2% and 4.9% when the superheat temperatures are 17, 25, 33 and 41 °C, respectively. The central equiaxed grain ratio obviously decreases with an increase of superheat temperature. The shell thickness out of the mould becomes thin, and the thermal capacity becomes strong when the superheat temperature decreases. Low casting temperature of molten steel helps to promote nucleation, which is beneficial to get high equiaxed zone ratio.

As can be seen in Fig. 9, the equiaxed crystal ratio deceases and the grain size refines with an increase of superheat temperature. Based on the present simulation and industrial test, it is concluded that the superheat temperature below 25 °C is the best temperature to obtain the desired solidification microstructure. It is because the bulk nucleation sites decrease and the undercooling at the front of solid/liquid interface decreases with the increasing superheats. All the factors affect positively the growth of columnar dendrite. The higher equiaxed ratio can be obtained by lowering the superheat in the manufacturing process.

Our propose is to study the best casting speed and superheat so as to obtain low degree of segregation blooms. Then, 10 samples are selected in the manufacturing field. These samples are etched with hydrochloric acid-water solution to reveal the solidification structure from the area fraction of columnar and equiaxed zones are measured. The maximum segregation of C is correlated to the area percent of equiaxed zone which is shown in Fig. 10 with the casting speed 0.60 m/min and the super heat no more than 25 °C. In Fig. 10, these samples are 60% below the degree of centre segregation 1.05 with the equiaxed zone ratio of 8%-10%.

Fig. 8 Simulated solidification microstructure distribution at different casting temperatures:

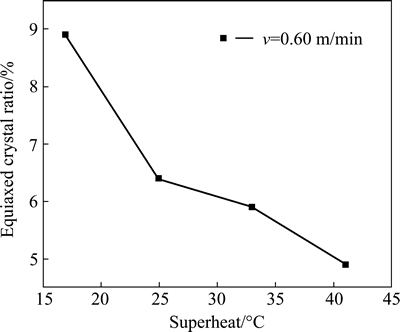
Fig. 9 Influence of casting temperature on equiaxed crystal ratio

Fig. 10 degree of centre segregation of carbon with equiaxed crystal ratio

5 Conclusions

1) A mathematical model is built to simulate solidification structure of 13Cr bloom in continuous casting process coupled with heat transfer model and CA-FE method. The physical properties related to simulation of the solidification structure are measured. Considering variation of technological parameters during the solidification, the simulation results of the temperature field and equiaxed crystal ratio show a good agreement with the measured data in the real bloom.

2) Given the actual conditions of the bloom caster, the optimum casting speed (0.60 m/min) and superheat temperature (below 25 °C) are obtained for the larger equiaxed crystal ratio. These samples selected in the manufacturing field are tested, with more than 60% below the degree of centre segregation 1.05 with the equiaxed zone ratio of 8%–10%.

3) The effect of the casing parameters and the solidification microstructure can be studied by the new coupled model.

References

[1] CHOUDHARY S K, GANGULY S. Morphology and segregation in continuously cast high carbon steel billets [J]. ISIJ International, 2007, 47(12): 1759-1766.

[2] M, ROMERO-ROMO M A, R. Computational algorithms to simulate the steel continuous casting [J]. International Journal of Minerals, Metallurgy and Materials, 2010, 17(5): 596-607.

[3] ABOUTALBELDL M, HASAN M, GUTHRIE R. Coupled Turbulent flow, heat and solute transport in continuous casting processes [J]. Metallurgical and materials transactions B, 1995, 26(4): 731-744.

[4] VENKATESANA A, GOPINATHB V, RAJADURAIB A. Simulation of casting solidification and its grain structure prediction using FEM [J]. Journal of Materials Processing Technology, 2005, 168: 10-15.

[5] LUO Sen, ZHU Miao-yong, LOUHENKILPI S. Numerical simulation of solidification structure of high carbon steel in continuous casting using cellular automaton method [J]. ISIJ International, 2012, 52(5): 823-830.

[6] RAPPAZ M, GANDIN C. Probabilistic modelling of microstructure formation in solidification processes [J]. Acta metallurgica et Materialia, 1993, 41(2): 345-360.

[7] NASTAC L. Numerical modeling of solidification morphologies and segregation patterns in cast dendritic alloys [J]. Acta Materialia, 1999, 47(17): 4253-4262.

[8] NATSUME Y, OHSASA K, NARITA T. Phase-field simulation of transient liquid phase bonding process of Ni using Ni-P binary filler metal [J]. Materials Transactions, 2003, 44(5): 819-823.

[9] ZHAN Xiao-hong, WEI Yan-dong, DONG Zhi-bo. Cellular automaton simulation of grain growth with different orientation angles during solidification process [J]. Journal of Materials Processing Technology, 2008, 208: 1-8.

[10] LI Xiang-mei, ZHANG Jie-yu, WANG Bo, REN Zhong-ming, ZHOU Guo-zhi. Simulation of stray grain formation during unidirectional solidification of IN738LC superalloy [J]. Journal of Central South University of Technology, 2011, 18(1): 23-28.

[11] YAO Ke-fu, QIAN Bin, SHI Wei, LIU Chun-cheng, LIU Zhuang. Experimental study and numerical prediction of phase transformation evolution during temperature process of martensite [J]. Acta Metallurgica sinica, 2003, 39(8): 892-896. (in Chinese)

[12] CHEN Jia-xiang. Iron and steel metallurgy [M]. Beijing: Metallurgical Industry Press, 1990. (in Chinese).

[13] LALLY B, BIEGLER L, HENEIN H. Finite difference heat-transfer modelling for continuous casting [J]. Metallurgical and Materials Transactions B, 1990, 21(4): 761-770.

[14] MIRIHANAGE W U, DAI Hui-juan, DONG Hong-biao, BROWNE D J. Computational modelling of molumnar to equiaxed transition in alloy solidification [J]. Advanced Engineering Materials, 2013, 15(4): 216-229.

[15] THEVOZ P, DESBIOLIES J, RAPPAZ M. Modeling of equiaxed microstructure formation in casting [J]. Metallurgical Transactions A, 1989, 20(2): 311-322.

[16] KURZ W, GIOVANOLA B, TRIVEDI R. Theory of microstructural development during rapid solidification [J]. Acta Metallurgica, 1986, 34(5): 823-830.

[17] CHEN Jia-xiang. Continuous casting handbook [M]. Beijing: Metallurgical Industry Press, 1991. (in Chinese)

(Edited by YANG Hua)

Foundation item: Projects(51274057, 51474057) supported by the National Natural Science Foundation of China; Project(2012AA03A508) supported by the High-tech Research and Development Program of China

Received date: 2014-11-24; Accepted date: 2015-03-19

Corresponding author: LI Ying, Professor; Tel: +86-24-83688995; E-mail: liying@mail.neu.edu.cn