DOI： 10.11817/j.issn.1672-7207.2020.10.023

圆盘节理模型的量化评价与优化方法

刘铁新¹，郑俊²，刘爱娟³，郑洪春³

(1. 大连海事大学 土木工程系，辽宁 大连，116026；

2. 浙江大学 建筑工程学院，浙江 杭州，310058；

3. 中国长江三峡集团有限公司，北京，100382)

摘要：为定量评价与改进圆盘节理模型的建模精度，对经典块体理论进行改进，并考虑结构面实际位置和尺寸，以便计算具体的关键块体体积。改进后，将关键块体体积作为定量指标，结合正交设计与极差分析，从稳定性角度对圆盘节理模型的关键参数进行判断。随后，依据实测迹线图与模型生成的迹线图分别计算关键块体体积，对比二者之间的差异，对模型的关键参数进行反演优化，使关键块体体积相等，从而得到更符合实际岩体情况的建模参数。研究结果表明：关键块体体积可量化反映模型与实际岩体之间的差异；体密度为圆盘节理模型中的关键因素；若关键参数不经过优化，则模型与实际岩体之间可能存在较大差距；关键参数经反演优化后，可保证模型与实际岩体在稳定性方面更加吻合。

关键词：圆盘节理模型；量化评价；块体理论；正交设计；反演优化

中图分类号：P642.3            文献标志码：A             开放科学(资源服务)标识码(OSID)

文章编号：1672-7207（2020）10-2917-08

Quantitative evaluation and optimization method of disk joint model

LIU　Tiexin¹, ZHENG　Jun², LIU　Aijuan³, ZHENG　Hongchun³

(1. Department of Civil Engineering, Dalian Maritime University, Dalian 116026, China;

2. Department of Civil Engineering, Zhejiang University, Hangzhou 310058, China;

3. China Three Gorges Corporation, Beijing 100382, China)

Abstract: In order to quantitatively evaluate and improve the modeling accuracy of disk joint models, the classical block theory was improved, and the actual position and size of the structural plane were considered so that the specific key block volume could be calculated. After the improvements, the volume of the key block was taken as a quantitative index, combined with the orthogonal design and range analysis, and the key parameter of the disc joint model was judged from the perspective of stability. Then, according to the measured trace map and the trace map generated by the numerical model, the volume of the key blocks were calculated respectively, and the differences between them were compared. The key parameters of the model were inverted and optimized to make the volume of the key blocks equal, and thus the modeling parameters were more consistent with the actual situation of the rock mass. The results show that the volume of the key block can reflect the difference between the model and the actual rock mass quantitatively. The density of discontinuity is the key factor in the disc joint model. Without optimization, there may exist large gap between the model and the actual rock mass. After the inversion optimization of the key parameters, the stability of the model and the actual rock mass is more consistent.

Key words: disc joint model; quantitative evaluation; block theory; orthogonal design; inversion optimization

岩体由结构面和结构体组成^[1]。由于岩石材料本身的遮光特性，使得精准掌握结构面在三维空间里的发育情况成为难题。为了研究岩体的稳定以及渗流等特性，岩体节理模型应运而生^[2]。根据模拟结构面时采用几何形状的不同，常见的节理模型可以分为圆盘模型、椭圆模型以及多边形模型等，圆盘模型因参数少及可靠性好等优点而应用较广^[3-8]。一般而言，圆盘节理模型的建立包含迹长分布拟合、产状分布拟合以及中心点分布拟合3个主要过程^{[3, 6, 8]}。其中，迹长和中心点分布拟合又分别与圆盘直径以及体密度等重要参数的计算有着直接关系。建模过程涉及参数计算较多，并且形式不一。近年来，众多学者围绕节理模型的参数计算、算法优化以及工程应用展开了研究^[9-13]。但由于建模假设的局限性以及参数计算的复杂性，致使模拟的结果与实际情况仍然存在一定差距。关于这种差距的评价以及改进方法，目前的相关研究较少，具体表现在如下2个方面：1) 差距的评价方面，缺乏量化指标。模型建立完成后，需要对其可靠程度进行检验。目前常用的检测方法有图形对比法、数值检验法等^{[9, 14-15]}。图形对比法多将模型剖面与实测露头面上的迹线图进行比较，得出定性结论。数值检验法将模型数据汇总后与现场对应的数据进行对比分析，从而得出定量结论。这些方法虽然使数值模型的准确程度有了评价指标，但对用于研究岩体稳定性的节理模型，这2种评价方法得出的结论不够准确，因为结构面的产状组合与分布位置对岩体的稳定性有显著影响。若不考虑结构面具体的空间位置与产状之间的耦合关系，则评价结果的可靠性较差。2) 差距的改进方面，对模型精度影响最大的关键参数尚不明确。圆盘节理模型的建立包含迹长分布拟合、产状分布拟合、中心点分布拟合、直径推断以及体密度计算等诸多过程。建模过程中涉及的参数计算较多，并且计算假定也较为严格。目前，人们从岩体的稳定性分析出发，对模型精度影响最大的关键参数研究较少，优化缺乏目标。为解决上述问题，本文作者利用块体理论在岩体稳定性评价方面可考虑结构面相对位置的优势，对其缺点进行改进，将关键块体体积(即开挖面或测窗面上所有的关键块体体积总和)作为圆盘节理模型的评价指标。基于此指标，从稳定性角度出发，利用正交设计与极差分析确定建模过程中的关键参数。最后，结合具体的工程实例对模型进行评价，并对关键参数进行反演，优化圆盘节理模型。

1  原理简介

本文将关键块体体积作为评价圆盘节理模型优劣的定量指标，结合正交设计和极差分析寻找对稳定性影响最大的关键参数。原理部分主要涉及经典块体理论改进以及正交设计2个方面。

1.1　经典块体理论改进

经典块体理论的核心思想是依据结构面的几何拓扑关系与极限平衡方法分辨块体类型，寻找有限可动的关键块体(如图1^[16]中块体5)。工程中寻找结构面危险组合的主要过程如下：首先，根据产状对岩体中的结构面进行分组；然后，按组确定每1组结构面的几何与力学参数(一般为均值)，主要包含产状、间距以及抗剪强度等；最后，根据几何拓扑关系以及极限平衡判断出岩体结构面的危险组合^[17]。经典块体理论假定结构面无限大，计算过程未充分考虑结构面的实际发育位置，很难获得开挖面上危险块体的具体位置和体积。若直接使用经典块体理论，则无法定量评价模型的优劣。本文结合节理模型剖切面上迹线的数据特征，对经典块体理论进行改进：一是对研究区域进行离散化处理；二是在小范围穷举搜索。

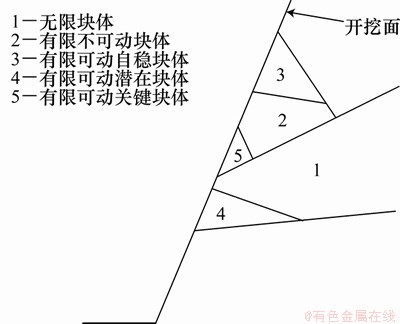
图1　块体类型示意图^[16]

Fig. 1　Schematic diagram of block types^[16]

以目前计算机的处理能力，按照研究区域直接进行关键块体全局搜索是不可行的。假定采集到1 000条结构面信息，仅四、五、六面体就需要进行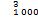C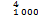+C+C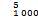=8.29×10¹²次搜索。为了减少运算次数，大的研究区域必须离散成小的胞元(图2中的方格称为胞元)。图2中，r(i，j)为相应胞元的搜索半径，胞元的中心选定为搜索的参考点。搜索范围须大于胞元的搜索半径，相邻的搜索范围要有一定的重叠。对于每个胞元，凡是落入该胞元搜索范围的结构面都将进入搜索列表。如果落入胞元1搜索范围的结构面编号为J₁，J₂，J₃和J₄，落入胞元2搜索范围的结构面编号为J₅，J₆，J₇和J₈，那么，对于四面体分析而言共有C³₄+C³₄=8种组合需要计算(块体中有1个面为开挖面，开挖面为固定的，因此，1个四面体只需选择出3个结构面即可)。关键块体采用矢量判别法进行判别，具体算法可参见文献[17-18]。由于每次搜索用到的结构面信息是确定的，所以，得到的关键块体体积也是唯一确定的。算法经改进后，任意1个结构面的位置、尺寸以及产状对岩体稳定性产生的影响都得到了充分考虑。

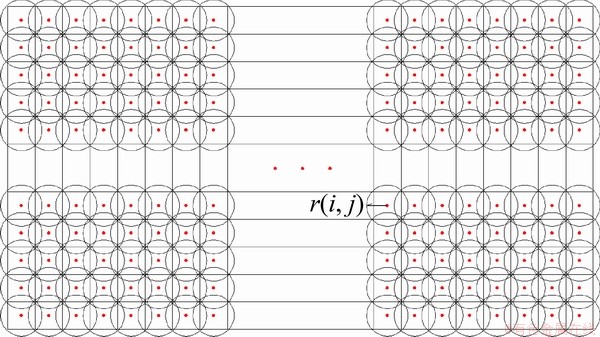
图2　研究区域离散图^[18]

Fig. 2　Discretization diagram of the study area^[18]

1.2　正交设计原理

正交设计是利用正交表设计试验方案的一种方法。通过正交试验可以获得因素之间的主次关系，同时也可极大程度地节约时间与经济成本。正交设计被广泛用于混凝土配合比选择、土石方抗剪强度的影响因素分析以及滑坡与滚石防护结构参数优化等诸多领域^[19-20]。常用的正交表有L₈(2⁷)，L₉(3⁴)和L₁₆(4⁵)等，可统一记为L_n(K^m)，其中L为正交表符号，n为实验次数，K为实验水平数，m为最大可分析因素个数。本文采用L₉(3⁴)正交设计表。

2  关键参数判别

圆盘节理模型主要由体密度、产状和直径这3个参数控制。获取岩体开挖面上的迹线信息后，根据文献[21-23]中的方法可以对这些参数进行计算。其中，体密度决定圆盘中心点的数量及位置，产状决定圆盘的空间方位，直径决定圆盘的大小。本部分以模型剖切面上(如图3中的测窗)关键块体体积为指标，研究上述3个参数的重要程度。通常而言，一般认为模型中心点服从泊松分布，产状服从Fisher分布，直径服从Gamma分布。利用正交设计与极差分析寻找影响最大的关键参数，每个参数分为3个水平，如表1所示。表1中，r₁~r₃分别为3个水平下不同参数对应关键块体体积的平均值，R为相应的极差。

表1　圆盘节理模型主要参数及计算结果

Table 1　Main parameters and results for disk joint model

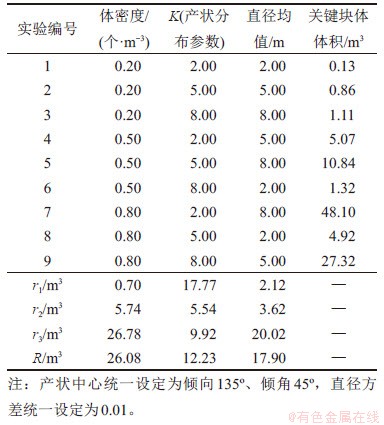
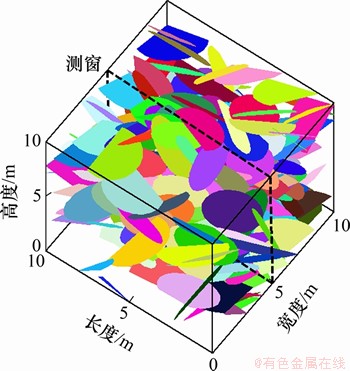
图3　圆盘节理模型示意图

Fig. 3　Disc joint model diagram

按照实验编号对应的参数建立圆盘节理模型，如图3所示，按测窗方位剖切后，模型中的结构面圆盘在剖切面上形成迹线图(如图4所示，图中每条迹线代表1个结构面，所有参数已知)。根据迹线图，结合1.1节内容搜索关键块体，获得每种参数组合对应的关键块体体积，见表1。由于数值模拟本身具有一定的随机性，每种参数组合计算100次，将平均值作为最终结果。从表1可以看出：结构面体密度对岩体稳定性影响最大，圆盘直径次之，产状影响最小，这是因为体密度决定着模型中结构面的数量。当体密度变化时，结构面数量会发生相应变化，增减结构面的变化也会导致产状以及圆盘直径发生变化，而产状以及圆盘直径的变化则不会影响体密度，因而，从岩体稳定性角度出发，体密度为圆盘节理模型中的关键参数。

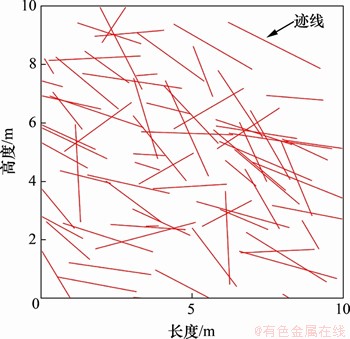
图4　模型迹线图

Fig. 4　Trace line map of the model

3  模型评价

本文以长河坝3号泄洪洞进口边坡1 670~1 680 m高程段为例展示节理模型的评价过程。对该区域内岩体结构进行近景摄影测量，3D图形信息如图5所示，开挖面的倾向为283°，倾角为78°。信息采集设备NIKON D7000以及35 mm的定焦镜头。据此图形进行数据提取，共提取963条结构面信息。将其位置以及尺寸信息导入Matlab中，开挖面上迹线延展情况如图6所示。经与现场卷尺罗盘数据对比，摄影测量数据精度满足工程精度要求。

图5　研究区域3D图(高程1 670~1 680 m)

Fig. 5　3D map of the study area(elevation from 1 670 m to 1 680 m)

图6　研究区域实测迹线提取图

Fig. 6　Real trace lines extraction of the study area

工程岩体内的结构面往往由多期地质构造运动形成，每期地质运动有自身特点，致使结构面的特征属性差别较大。建立模型前需要对其进行分组。本文以模糊均值法为基础，对研究区域内的结构面进行分组，结果如图7所示。

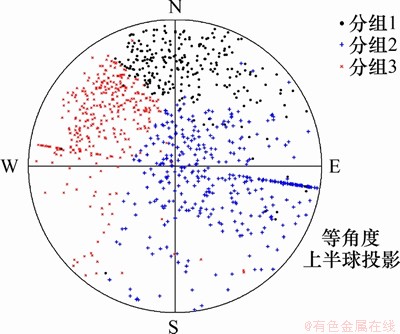
图7　研究区域结构面分组结果

Fig. 7　Discontinuities grouping result of the study area

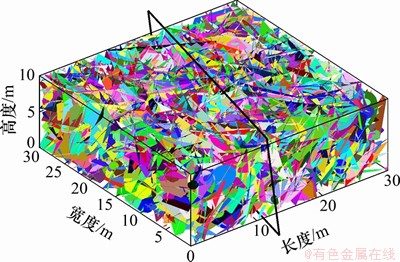
图8　岩体圆盘节理模型及相应剖面位置

Fig. 8　Rock mass model and profile location

将研究区域内的结构面分组完毕后，根据图6采集到的结构面信息，按组计算用于控制圆盘节理模型生成的方位、尺寸以及数量参数，计算结果如表2所示。根据表2中参数可以建立研究区域的圆盘节理模型，如图8所示。参数计算方法及建模过程参见文献[21-23]。按照边坡实际开挖面的产状信息对该节理模型进行剖切，在剖切面上可以得到模型的迹线分布图，如图9所示。

表2　实测结构面计算主要参数

Table 2　Main parameters of the measured discontinuities

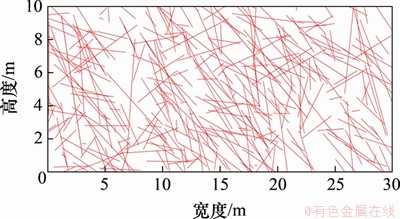
图9　研究区域拟合迹线图

Fig. 9　Fitting trace lines extraction map of the study area

对比图6和图9中迹线，发现二者区别较大。根据图中的迹线信息，利用本文1.1节中给出的相关方法，可以得到实际边坡上以及模型剖切面上的关键块体体积分别为27.4 m³和7.7 m³，二者相差较大，若直接将模型应用于岩体稳定性分析，则结果不符合实际，需要对模型进行优化。

4  模型优化

以结构面体密度作为优化指标，研究体密度变化过程中关键块体体积的变化规律，以便选择最优的体密度。为了分析体密度的影响，设计以下的计算模型。以表2每组结构面体密度为基准(其他参数不变)，乘以5个比例系数(由于关键块体体积模型的计算结果小于参考值，故比例系数大于1)，相邻的比例系数增幅相同，共计形成125种组合方式，计算每种体密度组合情况下形成的关键块体体积。研究区域内有3个结构面分组，将其比例系数分别记为x，y和z，将关键块体的体积记为w，根据关键块体体积的实际值可以在xyz坐标系中绘制出相应的等值面。图10所示为对应关键块体体积的等值面图。由图10可见研究区域内关键块体体积为27.4 m³时等值面的空间形态。

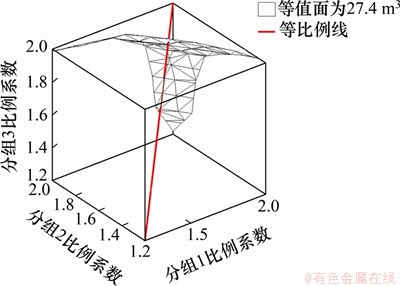
图10　关键块体体积等值面图(等值面为27.4 m³)

Fig. 10　Equivalent surface map of total volume of key blocks( equivalent surface is 27.4 m³)

为研究各组结构面相应体密度对关键块体体积的影响，轮流固定1个比例系数(x，y和z)，经过等值面切取2个剖面，每个剖面为只含有2个变量的关键块体体积等值线图，图11(a)~(f)所示为具体剖面的等值线图。

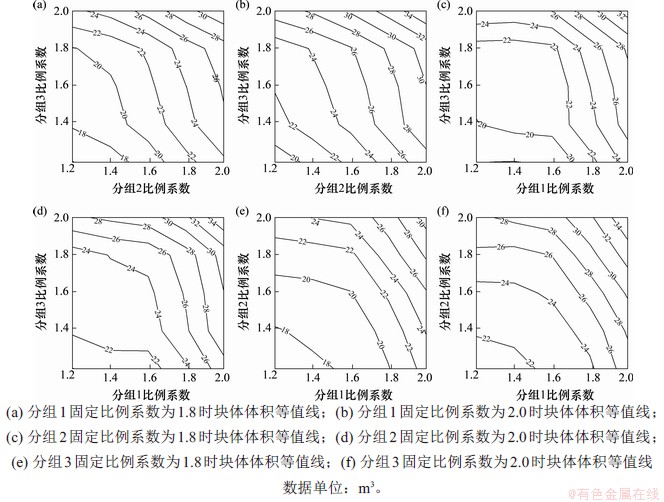
图11　块体体积等值线图

Fig. 11　Contour map of the total volume of block

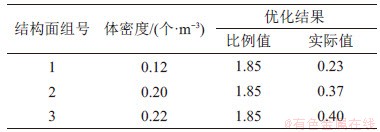
当研究区域内固定比例系数分别选为1.8和2.0，可变比例系数取值范围为1.2~2.0时，计算每种比例系数组合对应的关键块体体积，见表3。从表3可见：仅考虑比例系数时，分组1体密度的比例系数在增加1.6倍的过程中，关键块体体积的平均增量为6.1 m³，而分组2和分组3相应的平均增量分别为7.0和7.5 m³；将比例系数数值化后，单位体密度增量引起的关键块体体积增长的比例为1.00:0.69:0.65，可见分组1对稳定性的影响更为明显。同比例调整模型的体密度，使得模型计算值与实际值相同，得到优化后的体密度，如表4所示。实例部分工程岩体最终对应的建模参数(体密度除外)见表2。

表3　关键块体体积计算结果

Table 3　Calculation results of total volume of key blocks

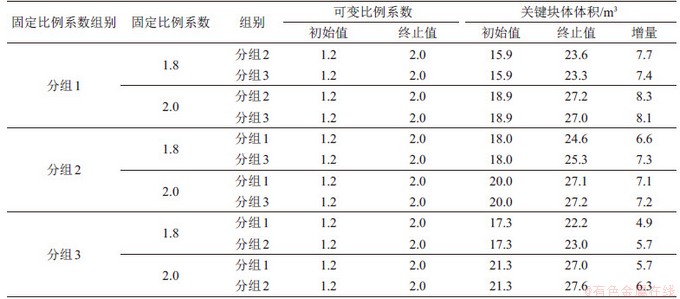
表4　体密度优化计算结果表

Table 4　Calculation results for volume density optimization

5  结论

1) 据改进后的块体理论，关键块体体积可量化反映模型与实际岩体之间的差异。

2) 从稳定性角度出发，根据极差分析结果，体密度为圆盘节理模型中的关键影响因素。

3) 不经优化，节理模型与实际岩体情况可能存在较大差距，以关键块体体积作为评价指标，两者相差较大。

4) 关键参数经反演优化后，可保证模型与实际岩体的稳定性更加吻合。

参考文献：

[1] 孙玉科, 李建国. 岩质边坡稳定性的工程地质研究[J]. 地质科学, 1965(4): 330-352.

SUN Yuke, LI Jianguo. Engineering geological studies of the stability of slope in rock[J]. Chinese Journal of Geology(Scientia Geologica Sinica), 1965(4): 330-352.

[2] LEI Qinghua, LATHAM J P, TSANG C F. The use of discrete fracture networks for modelling coupled geomechanical and hydrological behaviour of fractured rocks[J]. Computers and Geotechnics, 2017, 85: 151-176.

[3] KULATILAKE P H S W, WATHUGALA D N, STEPHANSSON O. Joint network modelling with a validation exercise in Stripa mine, Sweden[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1993, 30(5): 503-526.

[4] LIU Richeng, JIANG Yujing, LI Bo, et al. A fractal model for characterizing fluid flow in fractured rock masses based on randomly distributed rock fracture networks[J]. Computers and Geotechnics, 2015, 65: 45-55.

[5] DERSHOWITZ W S, EINSTEIN H H. Characterizing rock joint geometry with joint system models[J]. Rock Mechanics and Rock Engineering, 1988, 21(1): 21-51.

[6] 李新强, 杨松青, 汪小刚. 岩体随机结构面三维网络的生成和可视化技术[J]. 岩石力学与工程学报, 2007, 26(12): 2564-2569.

LI Xinqiang, YANG Songqing, WANG Xiaogang. Generation and visualization technologies of three-dimensional network of rockmass stochastic structural plane[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(12): 2564-2569.

[7] 吴顺川, 周喻, 高永涛, 等. 等效岩体随机节理三维网络模型构建方法研究[J]. 岩石力学与工程学报, 2012, 31(S1): 3082-3090.

WU Shunchuan, ZHOU Yu, GAO Yongtao, et al. Research on construction method of stochastic joints 3d-network model of equivalent rock mass[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(S1): 3082-3090.

[8] 郭亮, 李晓昭, 周扬一, 等. 数字化结构面三维随机网络模拟及其有效性检验[J]. 岩石力学与工程学报, 2015, 34(S1): 2854-2861.

GUO Liang, LI Xiaozhao, ZHOU Yangyi, et al. Simulation of random 3d discontinuities network based on digitalization and its validation test[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(S1): 2854-2861.

[9] 薛秋池, 赵其华, 何云松. 岩体结构面网络模拟的改进与应用[J]. 岩土工程学报, 2016, 38(7): 1351-1356.

XUE Qiuchi, ZHAO Qihua, HE Yunsong. Improvement and application of network simulation of rock mass discontinuities[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(7): 1351-1356.

[10] 杨超, 徐光黎, 申艳军, 等. 基于结构面网络模拟的节理岩质边坡可靠性分析[J]. 工程地质学报, 2014, 22(6): 1221-1226.

YANG Chao, XU Guangli, SHEN Yanjun, et al. Joint network simulation based reliability analysis for jointed rock slopes[J]. Journal of Engineering Geology, 2014, 22(6): 1221-1226.

[11] 张文, 陈剑平, 牛岑岑, 等. 基于三维裂隙网络RQD的确定及最佳测线数量的研究[J]. 岩土工程学报, 2013, 35(2): 321-327.

ZHANG Wen, CHEN Jianping, NIU Cencen, et al. Determination of RQD and number of optimum scanlines based on three-dimensional fracture network[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(2): 321-327.

[12] 张奇, 王清, 阙金声, 等. 基于凝聚层次聚类分析法的岩体随机结构面产状优势分组[J]. 岩土工程学报, 2014, 36(8): 1432-1437.

ZHANG Qi, WANG Qing, QUE Jinsheng, et al. Dominant partitioning of discontinuities of rock masses based on AGNES[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(8): 1432-1437.

[13] 贾洪彪, 唐辉明, 刘佑荣. 岩体结构面三维网络模拟理论与工程应用[M]. 北京: 科学出版社, 2008: 76-78.

JIA Hongbiao, TANG Huiming, LIU Yourong, et al. Theory and engineering application of 3-D network modeling of discontinuities in rockmass[M]. Beijing: Science Press, 2008: 76-78.

[14] 于青春, 大西有三. 岩体三维不连续裂隙网络及其逆建模方法[J]. 地球科学, 2003, 28(5): 522-526.

YU Qingchun, OHNISHI Y. Three-dimensional discrete fracture network model and its inverse method[J]. Earth Science, 2003, 28(5): 522-526, 544.

[15] 张国强, 张茹, 赵小平, 等. 岩体结构均质区划分的体视学方法研究初探[J]. 岩石力学与工程学报, 2011, 30(6): 1239-1249.

ZHANG Guoqiang, ZHANG Ru, ZHAO Xiaoping, et al. Preliminary research on scope of rock mass structural homogeneity zone using stereological interpretation[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(6): 1239-1249.

[16] UM J G, KULATILAKE P H S W. Kinematic and block theory analyses for shiplock slopes of the Three Gorges dam site in China[J]. Geotechnical & Geological Engineering, 2001, 19(1): 21-42.

[17] GOODMAN R E, SHI G. Block theory and its application to rock engineering[M]. Englewood Cliffs: Prentice-Hall, 1985:24-55.

[18] LIU Tiexin, DENG Jianhui, ZHENG Jun, et al. A new semi-deterministic block theory method with digital photogrammetry for stability analysis of a high rock slope in China[J]. Engineering Geology, 2017, 216: 76-89.

[19] 王江营, 曹文贵, 张超, 等. 基于正交设计的复杂环境下土石混填体大型直剪试验研究[J]. 岩土工程学报, 2013, 35(10): 1849-1856.

WANG Jiangying, CAO Wengui, ZHANG Chao, et al. Large-scale direct shear tests on soil-rock aggregate mixture under complicated environment based on orthogonal design[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(10): 1849-1856.

[20] 赵运会, 樊晓一. 基于正交设计的滑坡运动参数模型试验[J]. 山地学报, 2016, 34(1): 92-99.

ZHAO Yunhui, FAN Xiaoyi. Model test of movement parameters of landslide based on orthogonal design[J]. Mountain Research, 2016, 34(1): 92-99.

[21] ZHENG Jun, DENG Jianhui, YANG Xiaojuan, et al. An improved Monte Carlo simulation method for discontinuity orientations based on Fisher distribution and its program implementation[J]. Computers and Geotechnics, 2014, 61: 266-276.

[22] 张国强, 费文平, 张茹, 等. 节理泊松圆盘模型直径分布推断的解析方法[J]. 岩土力学, 2011, 32(4): 1149-1156.

ZHANG Guoqiang, FEI Wenping, ZHANG Ru, et al. Analytical method for estimating diameter distribution of Poisson disc joint model[J]. Rock and Soil Mechanics, 2011, 32(4): 1149-1156

[23] VILLAESCUSA E, BROWN E T. Maximum likelihood estimation of joint size from trace length measurements[J]. Rock Mechanics and Rock Engineering, 1992, 25(2): 67-87.

(编辑  伍锦花)

收稿日期： 2020 -02 -27; 修回日期： 2020 -05 -27

基金项目(Foundation item)：国家自然科学基金资助项目(41972264)；中央高校基本科研业务费资助项目 (3132019349) (Project(41972264) supported by the National Natural Science Foundation of China; Project(3132019349) supported by the Fundamental Research Funds for the Central Universities)

通信作者：郑俊，博士，副教授， 从事岩体稳定性研究；E-mail：zhengjun12@zju.edu.cn