J. Cent. South Univ. (2016) 23: 2276-2283

DOI: 10.1007/s11771-016-3285-8

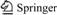
Design and simulation for large parafoil fix line object homing algorithm

LI Chun(李春)¹, TENG Hai-shan(滕海山)¹, ZHU Yan-hua(祝燕华)², JIANG Wan-song(蒋万松)¹,

ZHOU Peng(周朋)¹, HUANG Wei(黄伟)¹, CHEN Xu(陈旭)¹, LIU Jing-lei(刘靖雷)¹

1. Beijing Institute of Space Machine and Electricity, Beijing 100076, China;

2. School of Instrument Science and Engineering, Southeast University, Nanjing 210096, China

Central South University Press and Springer-Verlag Berlin Heidelberg 2016

Abstract: Traditional parafoil homing usually uses a point as object. As the mobility of parafoil is limited by its glide ratio and wind, in some cases when the parafoil scatter area is large, or the glide ratio of parafoil is small, the deviation of its landing point to object point will be arduous to control. Accordingly, during these situations, when parafoil is used in recovery of spacecraft or satellite, the landing area of parafoil can be set as a rectangle, and the object of parafoil can be set as a line segment. The thesis of this work is designing an algorithm for parafoil homing using line segment as object. The algorithm of wind velocity and direction calculation in different flying segments was also investigated. The algorithm designed navigates the parafoil to land into the predestined area and largely reduce the probability of recovery loads falling to unwanted area to damage houses and people.

Key words: fix line; homing; parafoil; algorithm; design; simulation

1 Introduction

Traditional circular parachute has been used for deceleration of aircraft returning as well as material airdrop. When the parachute is falling, it will be on status of uncontrollable and flying with the wind. The landing errors to objects are various from several to tens of kilometers. But the parafoil system has the character of sliding and falling to predestined area controllable. Using sparrow falling technology, it can even land with zero speed. The guidance, navigation and control system of parafoil has the functions of position measurement, homing operation, pulling and reposition of right and left manipulation strings for large parafoil. Consequently, it can control the movement path of parafoil and make it land close to predestined target point [1-5]. Traditional parafoil usually sets a fixed point on the landing area as object point. In some cases, the parafoil needs to land on a certain area, the object of parafoil can be set as a line. In this work, a kind of fix line object navigation algorithm for large parafoil is designed. The algorithm uses GPS positioning, direction measurement and speed measurement information as input data. It has the function of choosing the best landing point on predestined area automatically. And it can also calculate wind velocity and direction according to real-time homing trace automatically. A validation simulation for the algorithm is also performed.

2 Algorithm design

2.1 Analysis of segmental fix-point-object homing algorithm

At present, the algorithm of parafoil navigation control can be divided into three categories: simple homing, optimal control homing and segmental homing [6-12]. The characters of simple homing algorithm are controlling the direction of parafoil and making it identical with direction of the link line from the projection point to object point of parafoil. The algorithm of optimal control homing is finding the optimal solution which can make the object function enjoy the least control energy and minimum offset. Because precise parafoil aerodynamic model is arduous to find, the algorithm of optimal control homing is still on status of the oretical research and is extremely arduous to apply on project [13-15]. There are a lot of disturbance and random factors like wind to affect the performance of parafoil recovery and landing. Consequently, a kind of robust algorithm to minimize the affection of disturbance is needed. The main patterns of parafoil flying are gliding and turning, accordingly it is easy to divide its flying path into several segments. The algorithm of segmental fix-point-object homing is used in project widely. It usually chooses a point in the center of landing area as object point and divides the trajectory of parafoil homing process into several segments. The flying object of every segment is different [16-21]. Beijing Institute of Space Machine and Electricity, China has performed six times of parafoil airdrop experiment in September 2014 using the platform of fire balloon. The algorithm used in these experiments was segmental fix-point-object homing. The acreage of parafoil used in the airdrop experiment was 80 m², while the load was 1 t. The guidance navigation and control system of the parafoil used in the airdrop is shown in Fig. 1. The fire balloon platform is shown in Fig. 2. The flying processes of parafoil when it is turning in the sky and sparrow falling are shown in Figs. 3 and 4.

Fig. 1 Guidance navigation and control system used in airdrop experiment

Fig. 2 Fire balloon platforms used in airdrop experiment

Take the first flight of parafoil airdrop experiment for example. The altitude of its control begin point is 2197 m, while its landing point height is 1243 m. Accordingly the available control height is 954 m. The average slide ratios of these flights vary from 2.37 to 2.71. The slide ratio K can be calculated as

K=L/H                                      (1)

where L is slide distance and H is slide height. So the mobile ability L of the first flight can be calculated from 2259 m to 2583 m. Its homing ability area is shown in Fig. 5. In the graphic, the origin point of reference system is the object point of parafoil. The radius of object area circular is 300 m. The circular with radius from 300 m to 2259 m is area among which parafoil can fly to object area determinately. When parafoil begins its control flight in the circular with radius of 2259 m to 2583 m, it will fly to object area potentially. But if the control begin point of parafoil is farther than 2583 m, the possibility for the parafoil to reach the object area will be definitely low. The actual homing path of the first flight airdrop experiment is demonstrated in Fig. 6. The distances from control begin point and final landing point to object point are 1520 and 159 m, respectively.

Fig. 3 Turning process in parafoil airdrop experiment

Fig. 4 Sparrow falling process in parafoil airdrop experiment

Fig. 5 Homing ability area of first flight

Fig. 6 Actual homing path of first flight

2.2 Fix-line-object homing algorithm design

As upper example shows, if the control begin point of parafoil flight is further than its mobile ability, it will not reach the object area definitely as its control begin height is fixed. In some cases just like spacecraft or satellite recovery, the landing area can be bigger than a single point. During these situations, the object of parafoil should be set as a line segment. The acreage of parafoil controllable scattering area will be highly improved. Assume that when the parafoil falls from high altitude, if there is no recovery and homing control, the interspersing scope will be as large as a rectangle of L×W km². The area which the parafoil can land safely is a rectangle of L₁ km×W₁ km. This work sets ground object to be a line in the center of the safely landing rectangle, and the guidance, navigation and control (GNC) system of parafoil will calculate and choose optimal object point real-timely and automatically from the object line segment using the algorithm designed. The coordinates of object line’s two end points and the values of W₁ and L₁ can be pre-settled by program before parafoil takes off. The controllable parafoil scatter area and the chosen method of object line are demonstrated in Fig. 7.

When the parafoil releases from the sky, it takes a few seconds for the parafoil being stable and the global positioning system (GPS) researching enoughsatellites for navigation. Then the GNC system of parafoil will calculate real-time object point using the data received by GPS and the information of object line is pre-settled. When the calculation of real-time optimal landing point has finished, the GNC system of parafoil will calculate the navigation segment and choose a suitable mode. For different flying object corresponding to every flying segment, the real time steering variable is calculated by parafoil course angle and other essential parameters. Then the actuator of parafoil will execute corresponding instructions to steer the flying direction of parafoil to make it land on the area as near as the object line. The graphics of homing segments and control process are demonstrated in Figs. 8 and 9. The control algorithm is demonstrated in Table 1, where R is the real-time distance between parafoil sub-point and real-time optimal object point, R₁ is the distance for the GNC of parafoil to change its first segment to the second, H is the real-time height of parafoil, H₁ and H₂ are essential heights for GNC system of parafoil to change its third and fourth segments.

Fig. 7 Ground line object setting schematic

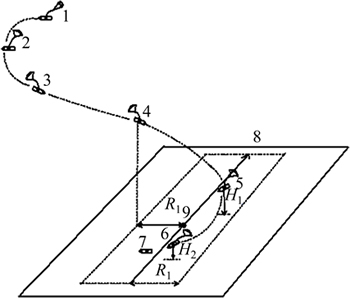
Fig. 8 Fix line object homing segments of parafoil (1—Parafoil release; 2—GPS gets position data; 3—Entrance fix direction homing segment; 4—Entrance energy manage segment;5—Entrance wind against landing segment; 6—Final landing segment; 7—Land; 8—Object line; 9—Optimal object point)

2.3 Calculation of real-time optimal object point

The calculation of real-time optimal object point is an intensely crucial step in the algorithm. This work uses traditional-parafoil-returning coordinate system. Taking the small range earth sphere as flat surface, the object line, parafoil sub-point and real-time optimal object point are all on the flat surface. The sub-point O of parafoil when T=T_i is the origin point of reference coordinate system. X axis is towards east, Y axis is towards north and Z axis is towards sky. It is called east-north-sky coordinate system. The function of object line segment is defined by two endpoints: P₁ and P₂. The coordinate of P₁ is (X₁, Y₁), while the coordinate of P₂ is (X₂, Y₂). The coordinate system is demonstrated in Fig. 10, the principle I and II are described in Figs. 11 and 12, respectively. And the calculation process is demonstrated in Fig. 13.

Fig. 9 Control process of navigation

Table 1 Control algorithm of navigation and control in different homing segments

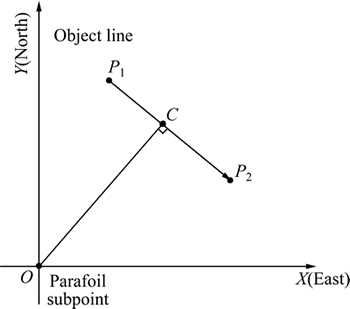
Fig. 10 Traditional-parafoil-returning coodinate system

The longitude and latitude values of two end-points P₁(λ₁, φ₁), P₂(λ₂, φ₂) on object line should be input into the GNC system of parafoil before parafoil takes off. They are decided by the area on which the parafoil is designed to land. While the GNC system of parafoil starts the navigation program, it will get the longitude and latitude information of Parafoil’s sub-point from GPS in a stable interval.

Assume that the longitude and latitude of parafoil’s sub-point gated by GPS are (λ₀, φ₀), where λ₀ is longitude and φ₀ is latitude. If the longitude and latitude of one certain point I on the landing area are (λ_I, φ_I), the coordinate of point I (X_I, Y_I) in return reference systemcan be calculated as

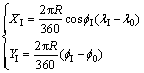                       (2)

where R is the average radius of earth and its value is 6371 km.

Consequently the coordinate (X₁, Y₁) and (X₂, Y₂) of object line’s two endpoints P₁ and P₂ in traditional parafoil-returning coordinate system can be calculated using Eq. (2). According to the coordinates of two endpoints, the function of object line can be expressed as:

                          (3)

The vertical line which begins from origin point O extending to object line can be expressed as

                              (4)

The coordinate of the two lines’ real-time crossover point C is (x′, y′). It can be calculated as

                                            (5)

Then the GNC system of parafoil should reset the start point of object line as P₁(X₁, Y₁) and end point as P₂(X₂, Y₂) using principle I and choose the real-time optimal object point A(X_a, Y_a) from P₁, P₂ or C using principle II. Then the longitude and latitude of real-time optimal object point A(λ_a, φ_a) can be calculated by

Fig. 11 Principle II for optimal object calculation

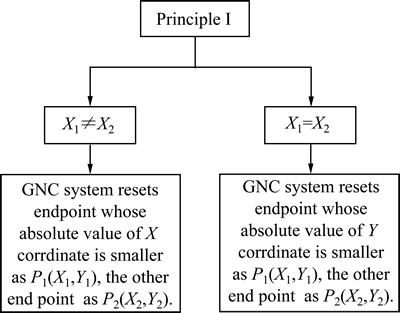
Fig. 12 Principle I for optimal object calculation

Fig. 13 Process for calculation of real-time optimal object point

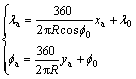                                              (6)

When the longitude and latitude of real-time optimal object point have been calculated, it can be used in navigation algorithm. When more accurate data are needed, more accurate earth radius data should be calculated. The average radius R of earth is 6371 km. Here the typical ellipsoid model is used. In typical ellipsoid model, the radius of certain point R′ on the earth surface can be calculated as

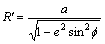                                                       (7)

where a is the long radius in the equatorial plane, and a=6378.137 km; e is earth ellipsoid eccentricity ratio and e=1/298.257; φ is the latitude data of parafoil sub-point given by GPS, which is close to the latitude data of optimal object point.

2.4 Calculation of real-time wind velocity

When the parafoil flies into the segment of wind against landing segment, it needs wind direction data as accordance for control. In other segment, if wind velocity has been fetched, the navigation will be more accurate. There are two kinds of method to fetch the wind direction data: wind direction sensor and software calculation. Two kinds of algorithm for wind calculation are introduced. During current process of navigation, only horizontal velocity is needed. Only the wind velocity in horizontal plane is considered.

Algorithm 1 is used in fix direction homing segment. During this segment, when the parafoil is getting into blind angle, no control steering is loaded. The variable of its direction is mainly affected by wind. As demonstrated in Fig. 14, the wind velocity can be calculated by

V_t2- V_t1=ΔV                                   (8)

The data of parafoil velocity vector in horizontal plane V_t1 and V_t2 can be fetched by GPS, where ΔV calculated by Eq. (8) is the real-time velocity of wind in horizontal plane.

Fig. 14 Algorithm 1 for wind direction calculation

Algorithm 2 is used in energy manage segment. Assume that wind direction is unchanged when the parafoil is spiraling in one circle, wind velocity can be calculated by comparing the absolute values of parafoil horizontal velocities in one circle. Between the parafoil horizontal velocities, V_n in one spiral circle which has the largest absolute value is V_l, while the other one which has the smallest absolute value is V_s. The wind velocity is expressed with V_w. Consequently the direction of V_w is the same as V_l and the absolute value of V_w can be calculated by

|V_w|=(|V_l|-|V_s|)/2                               (9)

The algorithm 2 is depicted in Fig. 15.

Fig. 15 Algorithm 2 for wind direction calculation

3 Simulation validate

The simulate calculation assumes that the parafoil’s disperse area is a rectangle with area of 70 km×60 km. Its homing object area is a rectangle of 60 km×20 km in the center of disperse area. The coordinate system for simulation takes the long center line of disperse area as X axis, the center point of X axis as origin point, and the vertical line of X axis crossing origin point as Y axis. The object line is chosen as the long center line of object area. Before simulation started, a slice of parafoil begin points is chosen from I, II, III and IV quadrants randomly. And the entrance speed of parafoil and wind speed are also random. The coordinates of these points chosen are demonstrated in Fig. 16.

The simulation result is demonstrated in Fig. 17. The black point with certain number is the initial point of certain parafoil and the red point with the same number is the landing point of this parafoil. Consequently the distance to the objective line could be expressed as the Y coordinate of the parafoil’s landing point. The result indicates that using the algorithm introduced the parafoil can reach the homing object area in most cases. But in some extreme conditions, such as when the line direction which begins from parafoil sub-point to real-time object point is almost the same as the direction of wind coming, and the horizontal speed value of parafoil is almost equal to the horizontal speed value of wind coming, the mobility of parafoil is restrained by wind largely. In this case, if the parafoil’s entrance point is far from the optimal object point, it will be arduous to reach the homing object area.

Fig. 16 Beginning points chosen for parafoil

Fig. 17 Simulation result of parafoil fix line algorithm

4 Conclusions

1) The algorithm used in the case for large parafoil fix line homing is designed. Using this algorithm, the GNC system of parafoil can lead the parafoil to land into fix area and reduce the probability of individuals or material damage during the process of spacecraft or material recovery when fix point homing is unrealized.

2) A simulation is performed and it is validated that the algorithm is effective. An airdrop experiment using this algorithm is performed in the next research step for more validation.

References

[1] DAVID C, SEAN G, PHILIP H, LEENA S. Autonomous guidance, navigation, and control of large parafoils [R]. Munich, Germany: 18th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, 2005.

[2] STEVE T, GREG N, ANTHONY D, PAUL S, COLIN M, GLEN B. Advanced sensors for precision airdrop [R]. Seattle, Washington: 20th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, 2009.

[3] SIM A G, MURRAY J E, NEUFELD D C. Development and flight test of a deployable precision landing system [J]. Journal of Aircraft, 1994, 31(5): 1101-1108.

[4] MURRAY J E, SIM A G, NEUFELD D C, PATRICK K, NORRIS S R, HUGHES W S. Further development and flight test of an autonomous precision landing system using a parafoil [R]. California: Dryden Flight Research Center, 1994.

[5] VINDHYA D. Developments in unmanned powered parachute aerial vehicle: A review [J]. IEEE A&E System Magazine, 2014, 11(1): 6-13.

[6] LI Chun, LV Zhi-hui, HUANG Wei. Software design of guidance navigation control system for controllable parafoil [J]. Journal of Beijing University of Technology, 2013, 39(7): 1034-1039. (in Chinese)

[7] LI Chun, Zhi-hui, HUANG Wei, SHEN Chao. Guidance navigation & control system for precision fix-point homing parafoil [J]. Journal of Central South University: Science and Technology, 2012, 43(4): 1331-1335. (in Chinese)

[8] XIONG Jing. Research on the dynamics and homing project of parafoil system [D]. Changsha: School of Aerospace and Materials Engineering, National University of Defense Technology, 2005. (in Chinese)

[9] WARD M, COSTELLO M. Adaptive glide slope control for parafoil and payload aircraft [J]. Journal of Guidance Control and Dynamics, 2013, 36(4): 1019-1034.

[10] DELLICKER S, BENNEY R, BROWN G. Guidance and control for flat-circular parachute [J]. Journal of Aircraft, 2001, 38(5): 809-817.

[11] ROSICH A, GURFIL P. Coupling in-flight trajectory planning and flocking for multiple autonomous parafoils [J]. Proceedings of the Institution of Mechanical Engineers Part G-Journal of Aerospace Engineering, 2012, 226(G6):691-720.

[12] LI Feng, QI Xiao-hui, LI Yu-hui. Design of unpiloted powered parafoil flight control system [J]. Ordnance Industry Automation, 2008, 27(2): 82-83. (in Chinese)

[13] ZHU Er-lin, SUN Qing-lin, TAN Pan-long, CHEN Zeng-qiang, KANG Xiao-feng, HE Ying-ping. Modeling of powered parafoil based on Kirchhoff motion [J]. Nonlinear Dynamics, 2015, 79: 617-629.

[14] ZHANG Li-min, GAO Hai-tao, CHEN Zeng-qiang, SUN Qing-lin, ZHANG Xing-hui. Multi-Objective global optimal parafoil homing trajectory optimization via Gauss pseudospectral method [J]. Nonlinear Dynamics, 2013, 72: 1-8.

[15] LI Ming-ming, LU Hong-qian, YIN Hang, HUANG Xian-lin. Novel algorithm for geomagnetic navigation [J]. Journal of Central South University, 2011, 18(3): 791-799.

[16] PU Zhi-gang, LI Liang-chun, TANG Bo, ZHANG Yong. Control method for multiphase homing orientation of parafoil system [J]. Journal of Sichuan Ordnance, 2009, 30(10): 117-119. (in Chinese)

[17] CHEN Rui-ming. Homing method research of precision landing of parafoil system [J]. Spacecraft Recovery & Remote Sensing, 2005, 26(1): 18-23. (in Chinese)

[18] van der KOLF G. Flight control system for an autonomous parafoil [D]. Cape Town: Department of Electrical and Electronic Engineering, Stellenbosch University, 2013.

[19] SLEGERS N, BROWN A, ROGERS J. Experimental investigation of stochastic parafoil guidance using a graphic processing unit [J]. Control Engineering Practice, 2015, 36: 27-38.

[20] ROGERS J, SLEGERS N. Robust parafoil terminal guidance using massively parallel processing [J]. Journal of Guidance, Control, and Dynamics, 2013, 36(5): 1336-1345.

[21] FOWLER L, ROGERS J. Bezier curve path planning for parafoil terminal guidance [J]. Journal of Aerospace Information Systems, 2014, 11(5): 300-315.

(Edited by FANG Jing-hua)

Foundation item: Project(61503077) supported by the National Natural Science Foundation of China; Project(BK20130628) supported by the Jiangsu Natural Science Foundation, China

Received date: 2015-06-12; Accepted date: 2015-11-02

Corresponding author: LI Chun, Associate Professor; Tel: +86-10-68114712; E-mail: bettynuaa@hotmail.com