进给驱动机构轴向振动与滚珠丝杠滚振研究
周勇,许学三,王国贤,曹小华
(武汉理工大学 物流工程学院,湖北 武汉,430063)
摘要:考虑扭转和轴向振动的滚珠丝杠副进给驱动机构建立动力学模型,对其固有动力学特性进行数值计算,提出进给驱动系统复杂振动中滚振的概念。利用MATLAB和ADAMS软件建立滚珠丝杠副进给驱动系统机电联合仿真平台,利用高分辨率旋转编码器和直线光栅尺等建立其动力学特性实验平台,对系统轴向和扭转动力学特性进行仿真分析与实验测量。实验结果表明:进给驱动机构第一阶模态在移动部件轴向振动的同时还存在滚珠丝杠的滚振,此滚振虽不会引起丝杠的扭转变形,但因其包含在伺服控制环之内,且频率较低、能量较大,会严重限制伺服控制带宽并影响其稳定性,在高性能进给驱动系统的设计中必须对此加以重视。
关键词:滚珠丝杠;进给驱动;轴向振动;滚振
中图分类号:TH113.1 文献标志码:A 文章编号:1672-7207(2013)10-4069-05
Study on axial vibration of feed drives and rolling vibration of ball screw
ZHOU Yong, XU Xuesan, WANG Guoxian, CAO Xiaohua
(School of Logistics Engineering, Wuhan University of Technology, Wuhan 430063, China)
Abstract: A dynamic model of the ball screw feed drives including torsional and axial vibrations was built and the natural dynamical characteristics of the system were numerically calculated. Then, the conception of rolling vibration was proposed to characterize an important part of the complex vibrations of the feed drives. A mechatronic integrated simulation framework of the ball screw feed drive system was built using MATLAB and ADAMS softwares and an experimental platform of dynamic characteristics including high resolution rotary encoder and linear encoder was established, which allows performing simulation analysis and field measuring to investigate the system dynamics in terms of torsional and axial vibrations. The results indicate that the ball screw’s rolling vibration is existent within the first mode of the feed drive system accompanying with the movable parts’ axial vibration. Although it does not cause ball screw’s torsional deformations, the rolling vibration shall seriously restrict the bandwidth of the servo control system and affect the system stability since it is contained within the servo control loop and possesses low frequency and high energy. The rolling vibration characteristics should be paid great attention in designing high performance feed drive systems.
Key words: ball screw; feed drive; axial vibration; rolling vibration
在滚珠丝杠副进给驱动系统中,要实现高伺服带宽和传动部件精密运动的精确控制,必须考虑其结构变形动力学行为对控制的影响,进而对控制系统提出有效的补偿。而其中扭转和轴向振动是对系统实现高带宽和高定位精度的决定性影响因素[1-3]。针对滚珠丝杠副进给驱动系统的动力学建模及其补偿控制问题,国内外研究者已开展大量工作。一些工作主要针对系统的轴向动力学进行,如:Kamalzadeh等[4]建立进给驱动系统的轴向动力学模型并采用自适应滑模控制方法对其轴向振动进行补偿;张佐营等[5]对精密滚珠丝杠副轴向振动的激励因素进行试验研究;张会端等[6]对工作台上刀具工作点的轴向振动进行建模和数值分析;Zhou等[7]对包含伺服电机的滚珠丝杠副进给驱动系统的轴向振动进行参数敏感性研究。另外一些工作则仅针对转子-丝杠系统的扭转振动展开,如Whalley等[8]研究进给驱动系统的扭转动力学频域响应及时域特性;Zhou等[9]研究工作台位置变化和工件质量变化对滚珠丝杠副驱动机构扭转振动固有特性的影响。更多的研究工作所建立的动力学模型则只包含系统轴向和扭转动力学模型,这些模型的建立通常采用集中参数法[10]、分布式参数法[11]和有限元方法[12]等。由于滚珠丝杠副进给驱动系统一般采用半闭环控制,其位置和速度反馈是从电机码盘或丝杠上安装的角度编码器获取,因此,转子-丝杠系统的扭转振动包含在控制系统的位置环和速度环之中。而移动部件的轴向振动频率一般较低,对零件的加工精度及表面质量具有较大影响,但由于半闭环控制系统中不测量移动部件的位移和速度,现有研究通常认为轴向振动对系统的控制带宽和稳定性影响较小。然而,滚珠丝杠副进给驱动系统是通过丝杠螺母副将丝杠的回转运动转换为移动部件的轴向运动,当移动部件发生轴向振动时,由于这种传动关系,可能同时会引起丝杠产生相应振动。本文作者建立含丝杠旋转和工作台移动的进给驱动机构动力学模型,通过对模型的数值分析提出滚珠丝杠滚振的概念,即滚珠丝杠的刚性回转振动(不产生扭转变形),并开展仿真和实验研究验证这种滚振的存在及其对伺服控制的影响。
1 滚珠丝杠副进给驱动机构动力学模型
采用集中参数方法,并假定移动部件处于丝杠中间位置,将滚珠丝杠副进给驱动机构划分为电机转子、联轴器输入端、联轴器输出端、滚珠丝杠前部、滚珠丝杠中部、滚珠丝杠后部和移动部件等7部分(图1),其中,滚珠丝杠被等分为前、中、后3部分。对于电机转子、丝杠等回转运动部件,考虑其转动惯量及各部件间的扭转刚度和阻尼。由于驱动机构的第一阶轴向振动模态通常以移动部件的轴向振动为主[12],建模时忽略回转部件间以及丝杠与轴承间的轴向刚度和阻尼,并忽略移动部件所受摩擦力,仅考虑移动部件与滚珠丝杠间的轴向刚度和阻尼。
图1中:I1,I2,…,I6分别为各回转部件的转动惯量;φ1,φ2,…,φ6分别为各回转部件的角位移;kt1,kt2,…,kt5及ct1,ct2,…,ct5分别为各回转部件之间的扭转刚度和阻尼;M和x分别为移动部件质量和直线位移;ka和ca分别为移动部件与丝杠之间的轴向刚度和阻尼;Tm为电机扭矩。
系统动能表示为
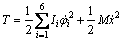 (1)
(1)
系统势能表示为
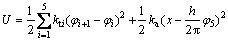 (2)
(2)
其中:h为丝杠导程。
引入耗散函数G,可得:
 (3)
(3)
则系统的拉格朗日方程为
 ,i=1,2,…,7 (4)
,i=1,2,…,7 (4)
其中:qi为广义坐标,q1=φ1,q2=φ2,…,q6=φ6,q7=x;Qi为广义坐标方向上的广义力,Q1=Tm,Q2=0;Q3=0,…,Q7=0。
将式(1)~(3)代入式(4),可得系统运动微分方程为:
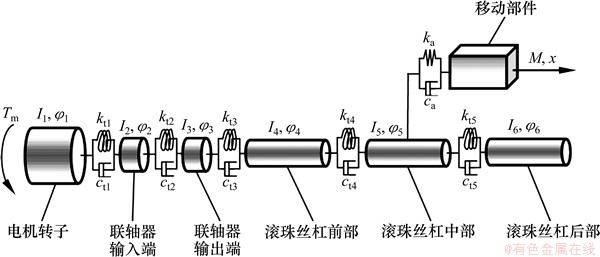
图1 滚珠丝杠副驱动机构动力学模型
Fig. 1 Dynamic model of ball screw feed drive mechanism
 (5)
(5)
式(5)可写成矩阵形式:
 (6)
(6)
其中:
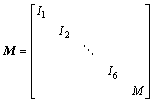
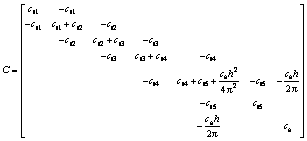
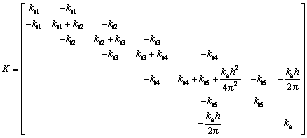
2 仿真与实验方法
2.1 仿真方法
仿真研究分2步进行:首先,根据所建立的滚珠丝杠副进给驱动系统动力学模型编制其自由振动微分方程的数值计算程序,通过求解其特征值和特征向量即可得到系统的固有频率和振型;其次,利用MATLAB和ADAMS软件建立滚珠丝杠副进给驱动系统的机电联合仿真模型[13],通过测量丝杠的角速度/角加速度和移动部件的速度/加速度对其动力学特性进行分析。图2所示为本文所研究的X-Y“十”字滑台的ADAMS动力学仿真模型,对X轴进行仿真分析,表1所示为X轴的主要参数。
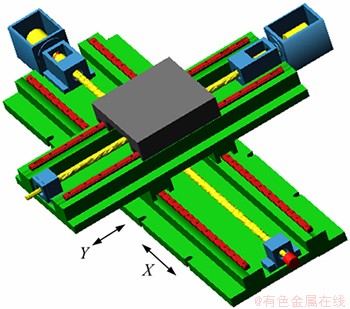
图2 X-Y十字滑台的ADAMS动力学仿真模型
Fig. 2 Dynamic model of X-Y cross sliding platform based ADAMS
表1 X轴主要参数
Table 1 Main parameters of X axis

2.2 实验装置及方法
实验装置如图3所示,主要包括滚珠丝杠副进给驱动系统(含数控装置、伺服驱动器、伺服电机、联轴器、滚珠丝杠、螺母和工作台等)、旋转编码器、直线光栅尺、计数卡以及计算机等。通过计数卡可实时测量安装在丝杠尾端的旋转编码器信号以及安装在拖 板/工作台上的直线光栅尺信号。旋转编码器为德国Heidenhain公司制造的ERN120系列,其物理分辨率为5 000线/转,经4倍频后可达到20 000个冲/转。直线光栅尺为珠海市怡信测量科技有限公司生产的GS11型,分辨率为0.001 mm。计数卡为阿尔泰科技制造的PCI2394型4轴正交编码器和计数器卡,通过PCI接口安装在计算机内,可同时测量4个通道的脉冲/方向信号。测量软件基于实时Linux系统开发,计数采样频率可达到10 kHz。
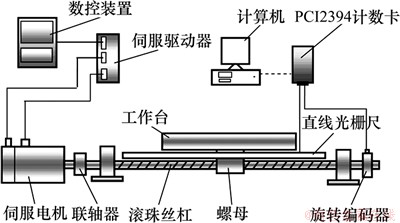
图3 测量装置示意图
Fig. 3 Sketch map of measuring equipment
3 仿真与实验结果
利用MATLAB软件编制滚珠丝杠副进给驱动机构的动力学数值计算程序,对X轴的固有振动特性进行分析。除去固有频率为0的刚体运动模态,图4所示为数值计算得到的X轴前2阶模态的固有频率及其振型图(取电机转子相对振幅为“1”),其中,Am点纵坐标为移动部件轴向振动折算到回转方向上的相对振幅,节点坐标取各部件质心相对电机转子质心的轴向距离。从图4可见:第一阶模态振型中各旋转部件的相对振幅均约为“1”,而移动部件的相对振幅约为“-0.45”,表明第1阶模态以移动部件的轴向振动与滚珠丝杠的滚振(即丝杠只产生刚性回转振动,基本无扭转变形)为主;第2阶模态主要表现为滚珠丝杠的单节点扭转振动(振型图上只有1个振幅为0的节点)。利用ADAMS/Vibration模块进行分析可得到一致的结果。
在MATLAB/ADAMS机电联合仿真平台和实验平台上,分别指令X轴作直线进给运动,取进给位移为25 mm,进给速度为6 000 mm/min,加速度为0.5g。截取匀速运动时的加速度信号作频域分析,图5所示为丝杠尾端角加速度信号的自功率谱幅频曲线,图6所示为丝杠尾端角加速度信号与拖板加速度信号的互功率谱幅频曲线(为保持单位一致,将拖板加速度折算为角加速度)。结合图4的固有振动特性分析结果,从图5和图6可见:拖板轴向振动与丝杠滚振的频率为19 Hz,丝杠单节点扭转振动频率为352 Hz,由于加入控制系统的影响,拖板轴向振动与丝杠滚振的实测频率比其固有频率有所降低。显然,由于频率较低且能量较大,滚珠丝杠滚振对半闭环伺服控制系统带宽和稳定性的影响远大于其扭转振动对系统的影响,在伺服控制环中,必须对此进行补偿和控制。
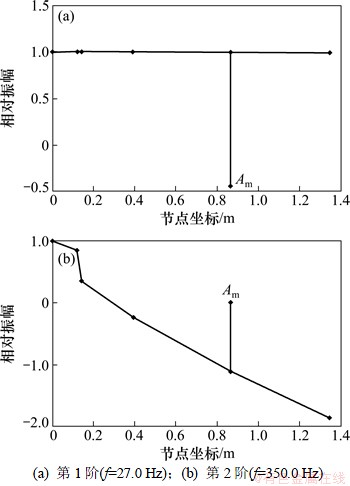
图4 X轴前两阶模态振型图
Fig. 4 Mode shapes of first two orders in X axis

图5 丝杠尾端角加速度信号的自功率谱幅频曲线
Fig. 5 Power spectrum density of angle acceleration in tail end of screw

图6 丝杠尾端角加速度信号与拖板加速度信号的互功率谱幅频曲线
Fig. 6 Cross power spectrum of angle acceleration in tail end of screw and acceleration of saddle
4 结论
(1) 采用集中参数法建立考虑扭转振动与轴向振动的滚珠丝杠副进给驱动机构动力学模型,进行动力学特性模拟,提出滚珠丝杠滚振的概念。
(2) 建立滚珠丝杠副进给驱动系统的MATLAB/ ADAMS机电联合仿真平台,利用高分辩率旋转编码器和直线光栅尺等建立其动力学特性研究实验平台。
(3) 系统第1阶模态以移动部件的轴向振动与滚珠丝杠的滚振为主,此滚振虽不会引起丝杠的扭转变形,但因其包含在伺服控制环之内,频率较低且能量较大,对半闭环伺服控制系统带宽和稳定性的影响远大于其扭转振动对系统的影响。
参考文献:
[1] Chen Y C, Tlusty J. Effect of low-friction guideways and lead-screw flexibility dynamics of high-speed machines[J]. Annals of CIRP, 1995, 44(1): 353-356.
[2] Erkorkmaz K, Kamalzadeh A. High bandwidth control of ball screw drives[J]. Annals of CIRP, 2006, 55(1): 393-398.
[3] Altintas Y, Verl A, Brecher C, et al. Machine tool feed drives[J]. Annals of CIRP, 2011, 60(2): 779-796.
[4] Kamalzadeh A, Erkorkmaz K. Compensation of axial vibrations in ball screw drives[J]. Annals of CIRP, 2007, 56(1): 373-378.
[5] 张佐营, 宋现春, 姜洪奎. 精密滚珠丝杠副轴向振动激励因素的试验研究[J]. 振动.测试与诊断, 2008, 28(1): 14-17.
ZHANG Zuoying, SONG Xianchun, JIANG Hongkui. Experiment study on exciting factors of axial vibration of precision ball screw[J]. Journal of Vibration,Measurement & Diagnosis, 2008, 28(1): 14-17.
[6] 张会端, 谭庆昌, 裴永臣. 机床工作台上刀具工作点的轴向振动分析[J]. 北京工业大学学报, 2008, 34(11): 1132-1138.
ZHANG Huiduan, TAN Qingchang, PEI Yongchen. Axial vibration analysis of the cutter’s work point of machine worktable[J]. Journal of Beijing University of Technology, 2008, 34(11): 1132-1138.
[7] Zhou Y, Peng F Y, Cao X H. Parameter sensitivity analysis of axial vibration for lead-screw feed drives with time-varying framework[J]. Mechanika, 2011, 17(5): 523-528.
[8] Whalley R, Ebrahimi M, Jamil Z. The torsional response of rotor systems[J]. Journal of Mechanical Engineering Science, 2005, 219(4): 357-380.
[9] Zhou Y, Peng F Y, Chen J H. Torsion vibration analysis of lead-screw feed drives with changeable table position and work-piece mass[C]//Proceedings of the 2007 IEEE International Conference on Mechatronics and Automation. Harbin: IEEE Press, 2007: 2194-2199.
[10] Chen J S, Huang Y K, Cheng C C. Mechanical model and contouring analysis of high-speed ball-screw drive systems with compliance effect[J]. International Journal of Advanced Manufacturing Technology, 2004, 24(3/4): 241-250.
[11] Varanasi K K, Nayfeh S A. The dynamics of lead-screw drives: low-order modeling and experiments[J]. ASME Journal of Dynamic System, Measurement, and Control, 2004, 126(2): 388-396.
[12] Smith D A. Wide bandwidth control of high-speed milling machine feed drives[D]. Florida: University of Florida, Department of Mechanical Engineering, 1999: 32-44.
[13] 周勇, 陈吉红, 彭芳瑜. 高速高精度数控进给驱动的机电联合系统仿真[J]. 机械科学与技术, 2007, 26(2): 135-139.
ZHOU Yong, CHEN Jihong, PENG Fangyu. Mechatronic integrated system simulation for a high-speed and high-precision CNC feed drive[J]. Mechanical Science and Technology, 2007, 26(2): 135-139.
(编辑 邓履翔)
收稿日期:2012-08-29;修回日期:2012-09-17
基金项目:国家自然科学基金资助项目(50975216);中央高校基本科研业务费专项资金资助项目(2011-IV-099)
通信作者:周勇(1973-),男,湖北汉川人,博士,副教授,从事机床动力学与振动控制等研究;电话:027-86532655;E-mail:zhoyo@163.com