Microscopic phase-field modeling of atomic anti-site behaviors in precipitation progress of Ni₃(AlFe)

LIANG Min-jie(梁敏洁)^{1, 2}, LIAO Hai-hong(廖海洪)², DING Wen-jiang(丁文江)¹, CHEN Zheng(陈 铮)³

1. School of Materials Science and Engineering, Shanghai Jiao Tong University, Shanghai 200240, China;

2. School of Materials Science and Engineering, North University of China, Taiyuan 030051, China;

3. School of Materials Science and Engineering, Northwestern Polytechnical University, Xi’an 710072, China

Received 15 October 2009; accepted 22 March 2010

Abstract: The effects of temperature on atomic anti-site behaviors in L1₂-Ni₃(AlFe) phases were studied using microscopic phase-field dynamic model in precipitation progress of Ni₇₅Al₂₀Fe₅ alloy. The results show that with the increase of temperature, the formation of Ni_Al and Al_Ni anti-sites is much easier in Ni₃(AlFe), and Ni and Al anti-site atoms show clearly stronger temperature-dependent than Fe anti-site atoms. The evolution progress of anti-site atoms is completed at the initial growth stage of L1₂-Ni₃(AlFe) phases. The site occupation probabilities of Ni atoms on the sublattice A (Ni_Ni, face centers sites of FCC), and Al and Fe atoms on the sublattice B (Al_Al and Fe_Al, corners sites of FCC) all present the degressive tendency with the temperature increasing. Fe atoms mainly prefer to occupy the Al sublattice at the whole temperature range.

Key words: anti-site; microscopic phase-field; precipitation; Ni₃(AlFe)

1 Introduction

In the initial precipitation progress of alloy, the formed precipitate phase is generally nanometer dispersion strengthening phase. γ'-Ni₃Al, with a large amount of long-range order of L1₂ structure up to the melting point, is one of the key strengthening components of the commercial nickel-base superalloys for high-temperature application due to its various outstanding properties[1-3]. However, the single crystal and polycrystal Ni₃Al has a low yield stress, which should be strengthened by the alloying method in order to eliminate the intercrystalline brittleness[4]. The addition of transition metal Fe has a drastic influence on the mechanical, electrical and magnetic properties of Ni₃Al[5-6], and it can improve the ductility and yield strength of Ni₃Al, which generally depends on the site occupation of Fe in Ni₃Al. However, the site occupation of Fe still has many diverges[7-9]. Thus, knowledge of site occupancy for Ni₃Al-Fe alloy in nanometer scale is of great importance to control and optimize the material properties.

For Ni₃Al with L1₂ structure, there exist two kinds of sublattices, i.e. A (face centers sites of FCC)and B (corners sites of FCC) sublattices predominantly occupied by Ni and Al atoms, respectively. Deviations from ideal stoichiometry Ni₃Al are accommodated by the formation of structural point defects (e.g. vacancies, anti-site and ternary substitutional atoms) on one or both sublattices[5, 10-11]. Anti-site defects as one kind of point defects have profound influence on alloy properties, such as diffusion, creep, hardness and strength[12]. So, the subject has therefore been investigated extensively by means of various experimental techniques and theoretical methods[5, 10-13].

However, there are few investigations focusing on the formation of anti-sites defects in ternary Ni₃Al-X system. Meanwhile, previous studies provided useful information of anti-site defects were mainly attained by the calculation of formation energies and the concentration change of defect[14]. Above results did not provide enough data for an accurate quantitative examination of anti-site behavior, and the temporal evolution of anti-site atoms during the formation of anti-site defects were not revealed in Ni₃Al-Fe systems.

In the present study, microscopic phase-field kinetic model will be extended to quantitatively evaluate the site occupation probability of anti-site atoms and site preference induced in the ternary Ni₃(AlFe) system which have important meaning for clarifying site preference and anti-sites evolution rules of atoms. In this work, it is assumed that the diffusion is completed by the atomic exchange, and the vacancy and the dislocation are neglected in the model.

2 Microscopic phase-field model

Microscopic phase-field kinetics model[15-16] was quickly developed as a new method of material simulation in recent years. Microcosmic crystal lattice diffusion theory was proposed by KHACHATURYAN[17], which makes composition relate to long range order parameter by nonequilibrium free energy of atom single-site occupation probability function, and can solve the kinetic equations of ordering and diffusion. However, the precipitation process of alloys is in nonequilibrium and nonlinearity, which can be well described by the microscopic diffusion equation.

Microscopic phase-field dynamic model was used to describe the atomic configurations and phase morphologies by single-site occupation probability. The ternary system microscopic phase-field dynamic model was developed by LI and CHEN[18]. In this model, P_A(r, t), P_B(r, t) and P_C(r, t) represent the probabilities of locating an A, B or C atom, at a given time t and a given lattice site r, respectively. Since P_A(r, t)+P_B(r, t)+P_C(r, t)=1, only two equations are independent at each lattice site. So, the microscopic diffusion equation of ternary system can be obtained[16]. In order to describe the nucleation, a random noise item was added to the right-hand side of the equation, and then the microscopic Langevin equations were given as

       (1)

where L_αβ(r-r?) is a constant related to the exchange probabilities of a pair of atoms, α and β, at lattice site r and r' per unit time, α, β= A, B or C. ζ(r, t) is the noise term which is taken to be Gaussian-distributed and its correlation properties meet the requirements of the fluctuation dissipation theory. k_B is the Boltzmann constant, and F is the total free energy of the system, based on the mean-field approximation:

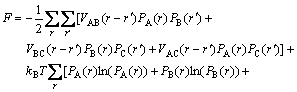
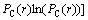                            (2)

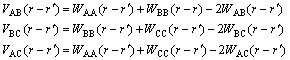                                (3)

where W_αβ(r-r′) is the pairwise interaction energy between a pair of atoms, α and β(=A, B, or C), at lattice site r and r′. They can be obtained either from first-principles calculations or by fitting them to the experimental phase diagram[16, 19]. The free energy is related to a function of pairwise interaction energies, site occupation probability, and the temperature. In this work, when the appropriate interaction energies are selected, free energy, which will vary with processes, is no longer a constant, and it process the non-linear characteristics. The relationship of free energy and temperature can be obtained from Eq.(2).

Substituting Eq.(2) into Eq.(1), after Fourier transforming of both sides of Eq.(1), the precipitation kinetic equations for ternary alloy system in the reciprocal space is obtained. Then, the Euler method is used to solve the equation. Finally, the relationships between site occupation probability on the lattice and time are acquired.

3 Results and discussion

3.1 Temporal evolution of atomic anti-site behavior

In Fig.1, the temporal evolution of anti-site atoms during the precipitation progress of Ni₇₅Al₂₀Fe₅ alloy is plotted as a function of time at 1 073, 1 173, 1 273, 1 333 K. At 1 073 K, during the initial incubation period of precipitation, since the matrix is in disorder state, the site occupation probabilities of Ni, Al and Fe atoms on the sublattice are all their original concentrations in alloy, respectively. As the ordering progress begins, the site occupation probability of anti-site atoms quickly decreases and almost arrives at the equilibrium value at the 3 800 time steps, which indicates that the ordering progress of L1₂-Ni₃(AlFe) phase has nearly been completed. Then, their values almost keep invariable. However, with increasing temperature, it can be seen that the incubation period of precipitation becomes longer and longer, in which the variations of anti-site atoms are very abnormal in view of the added thermal noise item at high temperature of 1 333 K. Corresponding course of anti-site atoms appears later and later; the velocity of their site occupation probability decreasing gradually tends to calm; their site occupation probability reaching the time steps of the equilibrium value is continuously postponed. In the whole precipitation progress, the anti-site behaviors of Ni_Al, Al_Ni and Fe_Ni all simultaneously proceed.

Fig.2 shows the variations of atomic site occupation probability on difference sublattices as the temperature increases for Ni₇₅Al₂₀Fe₅ alloy. From Fig.2(a), it can be seen that the occupation probabilities Ni_Al, Al_Ni and Fe_Ni all increase with the temperature rising, whereas Ni_Al and Al_Ni anti-sites show clearly stronger increase than Fe_Ni

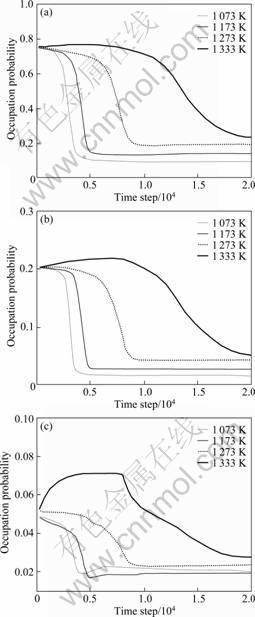
Fig.1 Temporal evolution of site occupation probability of anti-site atoms as function of time at different temperatures: (a) Ni_Al anti-sites; (b) Al_Ni anti-sites; (c) Fe_Ni anti-sites

anti-site with the temperature rising, and above 1 293 K, there are almost no more changes on Fe_Ni anti-site. These results imply that the formation of Ni_Al and Al_Ni anti-sites is much easier than that of Fe_Ni anti-site at high temperature, and Ni_Al, Al_Ni anti-sites show the strong temperature-dependent behavior, whereas, Fe_Ni anti-site is clearly weaker in Ni₃(AlFe) for Ni₇₅Al₂₀Fe₅ alloy. In Fig.2(b), with the increase of temperature, the site occupation probability of Ni atoms on the Ni sublattice (A sublattice), Ni_Ni, Al and Fe atoms on the Al sublattice (B sublattice), Al_Al and Fe_Al, all show decreasing tendency (in this work, Ni_Ni, Al_Al and Fe_Al are known as the atomic right-sites). Fig.2(b) indicates that atomic site occupation behavior is more and more deviated from ideal stoichiometry which are accommodated by anti-site and ternary substitutional atoms. So, the alloy system tends to be in the more disordered state when the temperature continuously increases.

Meanwhile, from Fig.2 we can see that site occupation probabilities of Fe atoms on Ni sublattices are less than 0.025, while on Al sublattices site occupation probabilities of Fe atoms are greater than 0.1. Therefore, Fe atoms mainly prefer to occupy the Al sublattices as the temperature increases. Table 1 presents the calculated site occupancy of Fe in Ni₃Al in comparison

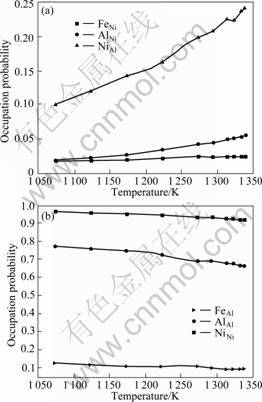
Fig.2 Variation rules of atomic site occupation probability on their anti-sites and right-sites as function of temperature: (a) Anti-sites (Ni_Al, Al_Ni and Fe_Ni); (b) Right-sites (Ni_Ni, Al_Al and Fe_Al)

Table 1 Comparison between this calculation and other results

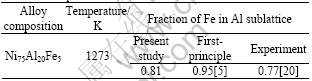
with the previous theoretical and experiment    studies[5, 20].

Using the atom location by channeling enhanced microanalysis (ALCHEMI) technique, SHINDO et al[20] studied the site occupation of Fe in Ni₃Al at 1 273 K. They indicate that Fe shows a weak but consistent preference for Al sublattice.

The site preference of Fe in Ni₃Al was investigated by JIANG et al[5, 11] as a function of temperature using first-principle calculations together with the Wagner- Schottky model. According to their study, in Ni-rich alloy, when the temperature is increased, the fraction of Fe in Al sublattice gradually decreases in Ni₃Al, but Fe shows a preference for the Al sublattice in the whole temperature range.

From above discussion, it is indicated that simulated results not only are in good agreement with the previous theoretical and experiment studies, but also quantitatively and clearly present the dynamic evolution progress of Ni, Al and Fe anti-sites. This exhibits the advantage of microscopic phase-field methods.

3.2 Evolution of volume fraction of Ni₃(AlFe) phases

Fig.3 shows the evolution of volume fraction of Ni₃(AlFe) phases as a function of time step at different temperatures. It can be seen that at 1 073 K, before 2 000 time steps the volume fraction has no fluctuation, which is the incubation period of precipitation. Subsequently, the value of volume fraction increases very quickly, which indicates that the ordered phases grow quickly. After 5 000 time steps, its value rises slightly, and this stands for the further growth and coarsening stage of the ordered phases. Combined with Fig.1, it can be seen that at 1 073 K during the incubation period of the precipitation, the site occupation probability of anti-site atoms keeps the original value, whereas, when the volume fraction of ordered phases quickly increases, reversely, the site occupation probability of anti-site atoms rapidly decreases, and then reaches the equilibrium value at 5 000 time steps. Then, during the continuous growth and coarsening stage of the ordered phases their site occupation probability already has no change. Furthermore, with continuously increasing temperature, it can be seen that the incubation period of precipitation becomes longer and longer (at 1 333 K, the volume fraction begins to present rising tendency till 14 000 time steps), and its equilibrium value gradually reduces. Meanwhile, it is further found that the time steps of the site occupation probability of anti-site atoms arriving at the equilibrium value are earlier and earlier than that in the case of volume fraction. Above results imply that in the evolution of anti-site atoms is already completed at the initial stage of L1₂-Ni₃(AlFe) phases growing, while it almost has no change at the later-stage of the growth and the coarsening stage of L1₂-Ni₃(AlFe) phases. This state is much more obvious with gradual increase of the temperature.

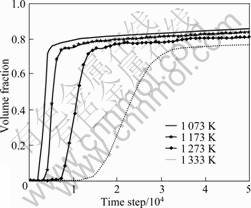
Fig.3 Variation of volume fraction of Ni₃(AlFe) phases with increasing time step at different temperatures

3.3 Evolution of atomic averaged long-range order parameter in Ni₃(AlFe)

The averaged long-range order (ALRO) parameter is the absolute value of the average of local long-range-order (LRO). Fig.4 shows the evolution of the ALRO parameters of both Fe and Al atoms in Ni₃(AlFe). Both the ALRO parameter values keep the original values at the initial stage which correspond to the incubation time of nucleation. Due to the added thermal noise items, at the initial stage of the precipitation, the ALRO parameter values of Fe atoms present the abnormal fluctuation. Then, both ALRO parameter values of Al and Fe atoms increase very quickly and reach the equilibrium values. However, with the increase of temperature, it can be seen that the incubation time of nucleation becomes longer, the rising velocity of the ALRO parameter slackens, and the values of the ALRO parameter decrease, which indicates that the ordering progress is prolonged and the degree of order is reduced. From Figs.1(b), (c) and Fig.4, it implies that only in this particle the anti-site progresses of Al and Fe atoms are earlier than average ordering progress of L1₂-Ni₃(AlFe) phases, whereas, the evolution of Al and Fe anti-site atoms is consistent with that of ALRO parameter from the whole tendency, which indicates that the ordering progress of L1₂-Ni₃(AlFe) phases is virtually evolution progress of atoms occupying the corresponding sublattice and their site occupation probabilities reaching their equilibrium values.

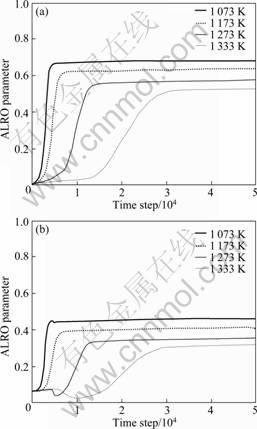
Fig.4 Evolution of ALRO parameter with time step in Ni₃(AlFe) phases at different temperatures: (a) Al atoms; (b) Fe atoms

4 Conclusions

1) For Ni₇₅Al₂₀Fe₅ alloy, with the increase of temperature, Ni_Al and Al_Ni anti-sites in Ni₃(AlFe) show obvious rising tendency, reversely, the change of Fe_Ni anti-site is very slight, which indicates that the formation of Ni_Al and Al_Ni anti-sites is much easier, and Ni and Al anti-site atoms show clearly stronger temperature- dependent than Fe anti-site atoms.

2) As the temperature increases, the site occupation probabilities of Ni atoms on the A sublattice (Ni_Ni right-sites) and Al and Fe atoms on the B sublattice (Al_Al, Fe_Al right-sites) present the degressive tendency. Fe atoms mainly prefer to occupy the Al sublattice, and at  1 273 K, the fraction of Fe in the Al sublattice is 0.81, which is in good agreement with other study results.

3) The evolution of anti-site atoms is already completed at the initial growth stage of L1₂-Ni₃(AlFe) phases, while it almost has no change at the later-stage of the growth and coarsening stage of L1₂-Ni₃(AlFe) phases, which is much more obvious with temperature increasing.

4) The evolution progress of Al and Fe anti-site atoms is consistent with that of ALRO parameter from the whole tendency, which indicates that the ordering progress of L1₂-Ni₃(AlFe) phases is virtually the evolution progress of atoms occupying the corresponding sublattice and reaching the equilibrium value.

References

[1] RUBAN A V, SKRIVER H L. Calculated site substitution in ternary γ′-Ni₃Al: Temperature and composition effects[J]. Phys Rev B, 1997, 55(2): 856-874.

[2] ALMAZOUZI A, NUMAKURA H, KOIWA M, HONO K, SAKURAI T. Site occupation preference of Fe in Ni₃Al: An atom-probe study [J]. Intermetallics, 1997, 5(1): 37-43.

[3] SUN Jian, LIN Dong-liang. Theoretical calculation of point defects in Ni₃Al[J]. Acta Metallurgica Sinica, 1993, 29(4): 171-175. (in Chinese)

[4] TAKASUGI T, IZUMI O, MASAHASHI N. Electronic and structural studies of grain boundary strength and fracture in Ll₂ ordered alloys—II: On the effect of third elements in Ni₃Al alloy[J]. Acta Metallurgica, 1985, 33(7): 1259-1269.

[5] JIANG C, GLEESON B. Site preference of transition metal elements in Ni₃Al [J]. Scripta Materialia, 2006, 55(5): 433-436.

[6] D’SANTHOSHINI B A, KAUL S N. Site preference of ternary Fe addition in Ni₇₅Al₂₅[J]. J Phys: Condens Matter, 2003, 15(29): 4903-4918.

[7] PASCARELLI S, BOSCHERINI F, LAWNICZAK- JABLONSKA K. Local structure of L1₂-ordered Ni₇₅(Al_1-xFe_x)₂₅ alloys[J]. Phys Rev B, 1994, 49(21): 14984-14990.

[8] LECHERMANN F, F?HNLE M AND SANCHEZ J M. First-principles investigation of the Ni-Fe-Al system [J]. Intermetallics, 2005, 13(10): 1096-1109.

[9] LIANG Min-jie, CHEN Zheng, ZHANG Ji-xiang, WANG Yong-xin. Microscopic phase-field simulation of atomic site occupation in the ordering process of NiAl9Fe6 alloy[J]. Transaction of Nonferrous Metals Society of China. 2008, 18(1): 59-62.

[10] SCHWEIGER H, SEMENOVA O, WOLF W, WOLFGANG P?SCHL, WOLFGANG P, PODLOUCKY R, IPSER H. Energetics of point defect formation in Ni₃Al[J]. Scripta Materialia, 2002, 46(1): 37-41.

[11] JIANG C, SORDELET D J, GLEESON B. Site preference of ternary alloying elements in Ni₃Al: A first-principles study [J]. Acta Materialia, 2006, 54(4): 1147-1154.

[12] PIKE L M, ANDERSON I M, LIU C T AND CHANG Y A. Site occupancies, point defect concentrations, and solid solution hardening in B2 (Ni,Fe)Al[J]. Acta Materialia, 2002, 50(15): 3859-3879.

[13] SHEN Jiang, WANG Yi, CHEN Nan-xian, WU Yu. First principles potential study of site preference substitution in Ni₃Al[J]. Progress In Natural Science, 2000, 10(6): 502-508. (in Chinese)

[14] LIU C T, FU C L, CHISHOLM M F, THOMPSON J R, KRCMAR M, WANG X L. Magnetism and solid solution effects in NiAl (40%Al) alloys[J]. Progress in Materials Science, 2007, 52(2/3): 352-370.

[15] CHEN L Q. Phase-field models for microstructure evolution[J]. Annu Rev Mater Res, 2002, 32(3): 113-140.

[16] PODURI R, CHEN L Q. Computer-simulation of atomic ordering and compositional clustering in the pseudobinary Ni₃Al-Ni₃V system[J]. Acta Mater, 1998, 46(5): 1719-1729.

[17] KHACHATURYAN A G. Theory of structural transformations in Solids[M]. New York: Wiley, 1983: 139.

[18] LI D Y, CHEN L Q. Computer simulation of morphological evolution and rafting of γ′ particles in Ni-based superalloys under applied stresses[J]. Scripta Materialia, 1997, 37(9): 1271-1277.

[19] GAUTIER F. High temperature alloys: Theory and design[M]. New York: Am Inst Min Engrs, 1984: 163-175.

[20] SHINDO D, KIKUCHI M, HIRABAYASHI M, HANADA S, IZUMI O. Site determination of Fe, Co and Cr atoms added in Ni₃Al by electron channeling enhanced microanalysis[J]. Trans Japan Inst Metals, 1988, 29(12): 956-961.

(Edited by LI Xiang-qun)

Foundation item: Project(50671084) supported by the National Natural Science Foundation of China; Project(2009021028) supported by Science and Technique Foundation for Young Scholars of Shanxi Province, China; Project(20100470125) supported by National Science Foundation for Post-doctoral Scientists of China

Corresponding author: LIANG Min-jie; Tel: +86-13621759370; Fax: +86-21-34202794; E-mail: lmj2005686@sina.com

DOI: 10.1016/S1003-6326(09)60402-7