J. Cent. South Univ. Technol. (2008) 15: 720-725

DOI: 10.1007/s11771-008-0133-5

Delay-independent decentralized H_∞ control for multi-channel discrete-time systems with uncertainties

CHEN Ning(陈 宁), GUI Wei-hua(桂卫华), CHEN Song-qiao(陈松乔)

(School of Information Science and Engineering, Central South University, Changsha 410083, China)

Abstract: A robust decentralized H_∞control problem was considered for uncertain multi-channel discrete-time systems with time-delay. The uncertainties were assumed to be time-invariant, norm-bounded, and exist in the system, the time-delay and the output matrices. Dynamic output feedback was focused on. A sufficient condition for the multi-channel uncertain discrete time-delay system to be robustly stabilizable with a specified disturbance attenuation level was derived based on the theorem of Lyapunov stability theory. By setting the Lyapunov matrix as block diagonal appropriately according to the desired order of the controller, the problem was reduced to a linear matrix inequality (LMI) which is sufficient to existence condition but much more tractable. An example was given to show the efficiency of this method.

Key words: multi-channel discrete-time system; time-delay; decentralized H_∞control; linear matrix inequality(LMI)

1 Introduction

The study of time-delay systems has received considerable interest in the last decades^[1-2]. Time-delay systems are frequently encountered in various areas, including engineering and economics. A time-delay is frequently a source of instability and poor performance in a system. Recently, robust stabilization^[3-5], guaranteed cost control^[6], dissipative control^[7] and H_∞ control^[8-10] of uncertain time-delay systems have been extensively investigated. GAO and WANG^[3] studied robust stabilization for uncertain discrete-time systems with multiple state delays. XU and CHEN^[8] studied delay- dependent guaranteed cost control for uncertain discrete time-delay systems via dynamic output feedback. But they did not consider the decentralized case.

Up to now, the robust output feedback control problem for multi-channel discrete-time systems with time-delay by linear matrix inequality(LMI) method still remains open. The model of interconnected large-scale system is a special case of multi-channel system. Therefore, the study of multi-channel discrete-time systems with time-delay is of practical value. For continuous time delay system, some results have been obtained^[11-13], in which the state-feedback control problem of large-scale interconnected systems was treated by the LMI method.

In this work, a robust decentralized H_∞control problem for multi-channel uncertain discrete-time systems with time-delay was considered. The uncertainties were assumed to be time-invariant, norm- bounded, and exist in system delay, control input and measurement output matrices. The existence conditions of decentralized H_∞controllers with the desired orders as LMIs were expressed by setting the Lyapunov matrix as block diagonal appropriately according to the controller’s order. Since the block sizes of the Lyapunov matrix can be allocated freely, an arbitrarily fixed order of the decentralized controller in this setting can be obtained. An example was given to show the efficiency of this method.

2 Problem description

Consider an uncertain N-channel discrete-time system with time-delay, which is described by

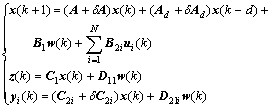  (1)

where 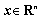 is the state; is the disturbance input; 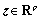 is the controlled output; 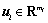and 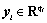are the control input and the measurement output of channel i (i=1, 2, …, N), respectively; d represents the time-delay; A, A_d, B₁, B_2i, C₁, C_2i, D₁₁ and D_21i are constant matrices with appropriate dimensions.

It is assumed that there is no unstable fixed mode with respect to the triplet (A, B_2i, C_2i). (δA, δA_d, δC_2i) denotes the uncertainties in the system, the delay, and the measurement output matrices, respectively. Suppose that

Δ

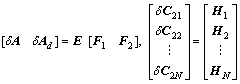        (2)

where  E, F₁, F₂, F₃ and H_i (i=1, 2, …, N) are known constant matrices, and Δ is an unknown constant matrix satisfying Δ^TΔ≤I.

Design a decentralized output feedback controller for system (1) as

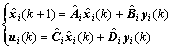                 (3)

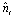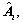
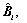
where  i=1, 2, …, N;  is the state of the ith local controller; is a specified order; 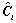and 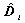are constant matrices to be determined. The closed-loop system obtained by applying controller (3) to system (1) is

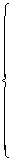
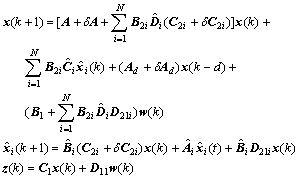(4)

The controller state 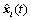and coefficient matrices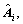 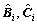 and 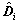 are collected as

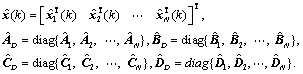
and matrices are defined as

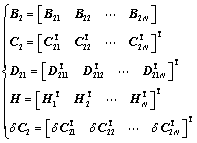              (5)

to describe the closed-loop system (4) as

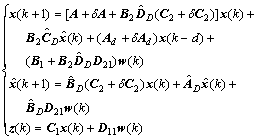  (6)

The matrices 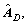  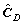and  are further written in a single matrix as

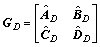                            (7)

and the notations are introduced

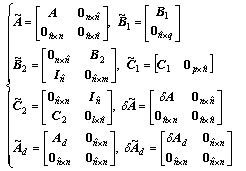      (8)

where 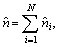  and 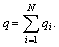Then system (6) is written in a compact form as

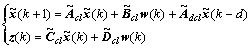     (9)

where

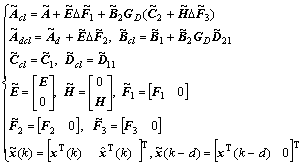(10)

In this description, only the controller coefficient matrix G_D is unknown, while all other matrices are given by system (1) and the uncertainties matrices (2).

The control problem of this work is to design an output-feedback controller (3) with a specified positive number γ, satisfying the following conditions.

1) Closed-loop system (9) is asymptotically stable when w(k)= 0;

2) Under the zero initial condition, the following condition is satisfied:

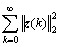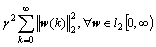≤        (11)

System (1) is said to be stabilizable with the H_∞disturbance attenuation level γ if the above conditions are satisfied.

3 Main results

To solve the decentralized control problem, the following lemma is employed.

Lemma 1^[14] Suppose X, E and F are matrices with suitable dimensions, X is symmetry matrix and Δ^TΔ≤1, then

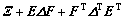＜0

if and only if there exists scalar ε＞0, satisfying

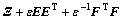＜0.

Assumption 1  Matrix B₂ has full column rank.

For simplicity, define notation.

A robust decentralizedcontroller is given as follows.

Theorem 1 For a given constant γ＞0, the discrete-time system (1) under Assumption 1 is stabilizable with the H_∞disturbance attenuation level γ via a decentralized controller (3) if there exists a positive definite matrix P structured as

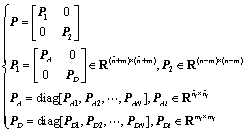       (12)

and 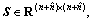 S＞0 and a matrix W_y structured as

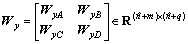              (13)

where

W_yA=diag{W_yA1, …, W_yAN}, W_yAi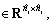

W_yB=diag{W_yB1, …, W_yBN}, W_yBi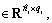

W_yC=diag{W_yC1, …, W_yCN}, W_yCi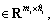

W_yD=diag{W_yD1, …, W_yDN}, W_yD1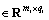

such that the LMI

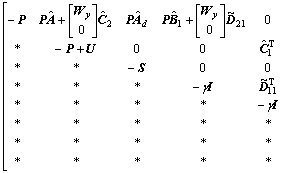
＜0                  (14)

holds. Here,

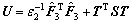                       (15)

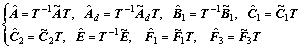(16)

where 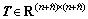is a nonsingular matrix satisfying

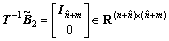                 (17)

When LMI (14) is feasible, a desired controller is computed as

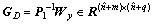                    (18)

Proof  Let the Lyapunov-Krasovskii functional for closed-loop system (9) be

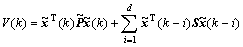      (19)

Then the forward difference is

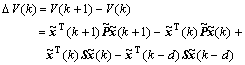
That is

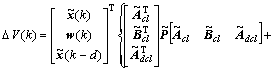
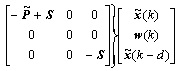         (20)

1) When w(k)=0, the difference of the Lyapunov-Krasovskii functional along close-loop system (9) using Schur complement can be characterized by

＜0               (21)

If Ω＜0 is satisfied, ΔV(k)＜0 is proved. For simplicity, the following non-singular transformation is introduced.

                            (22)

Pre-multiplying Eqn.(22) by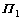and post- multiplying Eqn.(22) by  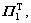yield

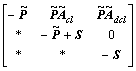＜0                   (23)

Substituting inequality (11) into inequality (23), one gets

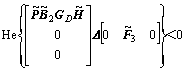                (24)

Using Lemma 1, inequality (24) can be rewritten as

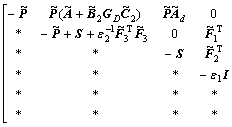
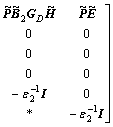＜0                 (25)

Let 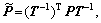according to Eqns.(17) and (18), we compute

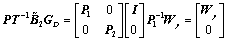        (26)

Let

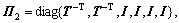pre-multiplying LMI (14) by Π₂ and post-multiplying LMI (14) by Π₂, and from the definition of  and Eqn.(18), using Schur complement, LMI (14) is reduced to inequality (25), i.e. ?V(k)＜0. Thus, discrete-time system (9) is asympto- tically stable.

2) Next, prove that inequality (11) is satisfied under the zero initial condition. For any non-zero 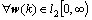, the performance is

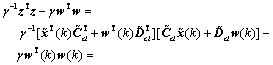
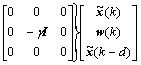                   (27)

Therefore,

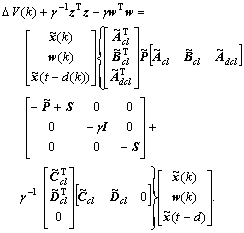
Based on the positive definiteness of ?V(k), the equivalent condition of 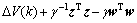＜0 is

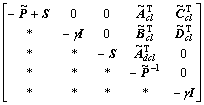＜0         (28)

Choose the following non-singular transformation as

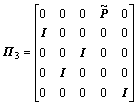                      (29)

Pre-multiplying (28) by 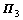 and post-multiplying (28) by 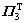, yield

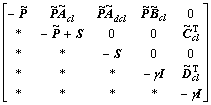＜0        (30)

Using Schur complement to inequality (30), one gets

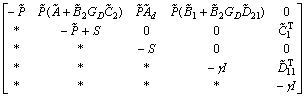
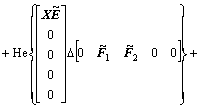
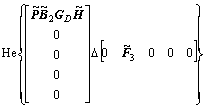＜0         (31)

Using Lemma 1 and condition (16), we have

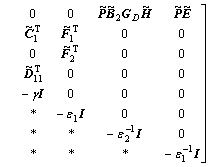 ＜0    (32)

Let 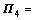diag{T^-T, T^-T, I, I, I, I, I, I}, pre- multiplying LMI (14) by  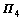and post-multiplying LMI (14) by 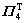, inequality (30) is obtained with the fact (26).

Therefore, if LMI (14) is satisfied, the inequality

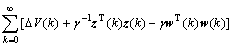＜0

holds. Thus,

≤

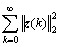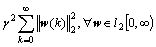
under the zero initial condition is satisfied.

The proof of Theorem 1 is completed.

Remark 1  It is understood from the above proof that the block diagonal structures of W_y and  P₁ are designed so that a decentralized output feedback controller is obtained, and the block diagonal structure of P is assumed so that the coupling between G_D and P can be removed by using some equivalent transformation. Although the structures of the variables are complicated at a first glimpse, matrix inequality (14) is linear with respect to S, P and W_y, and thus is very easy to solve by using the existing software LMI Control Toolbox^[15].

Remark 2  In this work, we extensively consider uncertainties in system matrix A, the time-delay matrix A_d and the measured output matrix C_2i. We can also treat the dual form of system (1) where uncertainties appear in system matrix A, the time-delay matrix A_d and the matrix control input B_2i as

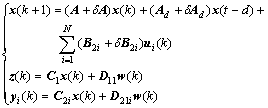  (33)

where  i=1, 2, …, N;

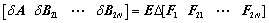  (34)

and E, F₁, F₂₁,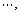F_2N are known constant matrices.

4 Example

In this part, an example was presented to show the usefulness of the method. System (1) is a two-channel system (N=2), where the input and the output of each channel are single, and the coefficient matrices are

,,,

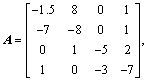
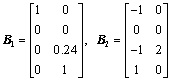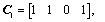
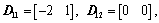
and the uncertainty matrices are defined by

Let the disturbance attenuation lever be γ=3.8, by solving the feasibility condition of Theorem 1, the first local controller is

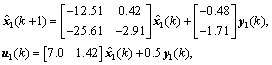
and the second local controller is

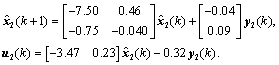
The singular value curve of system (1) via the obtained output feedback controller at d=10 is shown in Fig.1.

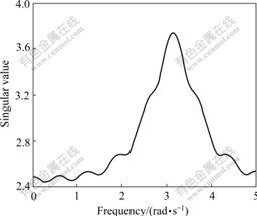
Fig.1 Singular value curve of system via obtained output feedback controller at d=10

5 Conclusions

1) The robust decentralized H_?  control problem for multi-channel uncertain discrete-time systems with time- delay is studied by Lyapunov-Krasovskii function. The uncertainties are assumed to be time-invariant, norm-bounded, and exist in system, time-delay, control input and measurement output matrices.

2) The existence conditions of decentralized H_∞controllers with desired orders as LMIs are expressed by setting the Lyapunov matrix as block diagonal appropriately according to the controller’s order.

3) Since the block sizes of the Lyapunov matrix can be allocated freely, an arbitrarily fixed order of the decentralized controller in this setting can be obtained.

References

[1] Niculescu R S. Delay effects on stability: A robust control approach [M]. London: Springer-Verlag, 2001.

[2] GU K, Kharitonov V L, CHEN J. Stability of time-delay systems (control engineering) [M]. New York: Springer-Verlag, 2003.

[3] GAO Hui-jun, WANG Chang-hong. Robust stabilization for uncertain discrete-time systems with multiple state delays [J]. Acta Automatica Sinica, 2004, 30(5): 789-795. (in Chinese).

[4] LIU Bi-yu, GUI Wei-hua, CHEN Ning. Delay-dependent output feedback decentralized robust control for discrete interconnected systems [J]. Acta Automatica Sinica, 2007, 33(6): 660-663. (in Chinese)

[5] ZHANG Xian-ming, WU Min, SHE Jin-hua, HE Yong, Delay-dependent stabilization of linear systems with time-varying state and input delays [J]. Automatica,2005, 41(8): 1405-1412.

[6] CHEN Wu-hua, GUAN Zhi-hong, LU Xiao-mei. Delay-dependent output feedback guaranteed cost control for uncertain time-delay systems [J]. Automatica,2004, 40(7): 1263-1268.

[7] LIU Bi-yu, GUI Wei-hua, WU Min. Passivity of interconnected control systems with time-delays based on decentralized control [J]. Control Theory and Applications, 2005, 22(1): 52-56.

[8] XU Sheng-yuan, CHEN Tong-wen. Robust H_∞ control for uncertain discrete-time systems with time-varying delays via exponential output feedback controllers [J]. Systems and Control Letters, 2004, 51(3/4): 171-183.

[9] ZHANG Xian-ming, WU Min. Delay-dependent H_∞control for linear discrete-time uncertain systems with multiple unknown delays [J]. Control Theory and Applications, 2006, 23(6): 918-922. (in Chinese)

[10] HE Yong, WU Min, SHE Jin-hua. Improved bounded-real-lemma representation and H_∞ control for systems with polytopic uncertainties [J]. IEEE Transactions on Circuits and Systems (Part II). 2005, 52(7): 380-383.

[11] CHEN Ning, GUI Wei-hua, XIE Yong-fang. Decentralized H_∞ state feedback control for large-scale interconnected uncertain systems with multiple delays [J]. Journal of Central South University of Technology, 2004, 11(1): 93-97.

[12] HU Z. Decentralized stabilization of large scale interconnected systems with delays [J]. IEEE Trans on Automatic Control, 1992, 39(1): 180-182.

[13] XU Bu-gong, XU Yi-fang, ZHOU You-xun. Decentralized stabilization of large-scale interconnected time-delay systems: An LMI approach [J]. Control Theory and Applications, 2002, 19(3): 475-478.

[14] PETERSEN I R. A stabilization algorithm for a class of uncertain linear systems [J]. Systems Control Letters, 1987, 8(1): 351-357.

[15] GAHINET P, NEMIROVSKI A, LAUB A J, CHILALI M. LMI control toolbox [M]. Massachusetts: The Math Works Inc, 1995.

(Edited by CHEN Wei-ping)

Foundation item: Project(60634020) supported by the National Natural Science Foundation of China; Project(07JJ6138) supported by Natural Science Foundation of Hunan Province, China; Project(20060390883) supported by the Postdoctoral Science Foundation of China

Received date: 2008-03-12; Accepted date: 2008-06-13

Corresponding author: CHEN Ning, PhD; Tel: +86-731-8879274; E-mail: ningchen@mail.csu.edu.cn