DOI: 10.11817/j.issn.1672-7207.2020.12.020
连续档架空线路动态风偏的多刚体模型
胡鑫,王璋奇,杨文刚
(华北电力大学 机械工程系,河北 保定,071003)
摘要:针对传统静力学分析方法无法计算架空线路的动态风偏响应、有限元方法模型复杂且运算时间长等问题,提出一种大风工况下连续档架空线路动态风偏的多刚体计算模型。首先,将架空线路绝缘子串视为质量均匀分布的刚性直杆,根据导线在风偏均值处摆动固有频率不变原则推导得出导线等效刚体模型,通过来流风与架空线路的相对运动考虑气动阻尼,运用分析力学方法,建立连续档架空线路动态风偏的多刚体模型与计算方法;其次,采用随高度变化的Kaimal风速谱和Davenport相干函数模拟脉动风场的空间分布,通过工程实例计算架空线路多刚体模型的动态风偏响应变化规律;最后,对多刚体模型进行模态分析,并将多刚体模型与传统静力学方法、有限元方法计算得到的工程实例风偏响应结果进行比较,验证多刚体模型的准确性与效率性。研究结果表明:架空导线自身柔性对绝缘子串风偏响应影响较小,连续档架空线路动态风偏多刚体模型能够准确高效地计算架空线路绝缘子串风偏角的动态响应变化规律,并可以有效呈现连续档架空线路中各个绝缘子串风偏运动的相对位置变化;相较于传统静力学分析方法,多刚体模型可以考虑架空线路风偏响应的动态特性,能够计算最大风偏角;相较于有限元方法,多刚体模型运算时间少,计算效率高。
关键词:连续档架空线路;绝缘子串动态风偏;多刚体模型;计算效率
中图分类号:TM75;O325 文献标志码:A
文章编号:1672-7207(2020)12-3465-10
Multi-rigid-body model of dynamic wind-induced deflection for overhead transmission lines
HU Xin, WANG Zhangqi, YANG Wengang
(Department of Mechanical Engineering, North China Electric Power University, Baoding 071003, China)
Abstract: Traditional static analysis method cannot calculate the dynamic wind-induced deflection response of overhead lines, and the finite element method(FEM) was complicated model and cost long calculation time. Aiming at the problems, a multi-rigid-body model for calculation of the dynamic wind-induced deflection response of overhead transmission lines under high wind conditions was proposed. Firstly, the insulator string was regarded as a rigid straight rod with uniform mass, and the equivalent rigid rod of conductor was derived based on the principle that the natural frequency of the conductor swings at the mean value of the wind-induced deflection is constant. The aerodynamic damping was calculated according to the relative movement of the incoming wind and the overhead line, and further the multi-rigid-body model of dynamic wind-induced deflection of overhead transmission lines was established by the analytical mechanics method. Secondly, the spatial distribution of the fluctuating wind field was simulated based on the Kaimal spectrum and the Davenport coherence function. On the basis, the variation law of dynamic wind-induced deflection response of the multi-rigid-body model of the overhead lines was obtained from an engineering example. Finally, the modal analysis of the multi-rigid-body model was carried out, and the wind-induced deflection responses obtained by the multi-rigid-body model were compared with those obtained by the traditional static method and FEM, which verified the accuracy and efficiency of the multi-rigid-body model. The results show that the flexibility of conductor has little effect on the wind-induced deflection response of the insulator strings. Moreover, the multi-rigid-body model can calculate the dynamic wind-induced deflection response of the insulator strings accurately and efficiently, which can present the relative position changes of the wind-induced deflection of each insulator string in the overhead transmission lines. Compared with the traditional static analysis method, the multi-rigid body model can calculate the dynamic wind-induced deflection angle of insulator string. Compared with FEM, the multi-rigid-body model costs less calculation time and has higher calculation efficiency.
Key words: overhead transmission lines; dynamic wind-induced deflection of insulator string; multi-rigid-body model; computational efficiency
随着电网建设的快速发展,线路走廊日益紧张,通过复杂地形及恶劣气候条件地区的架空线路日益增多,风偏闪络现象也愈发严重。架空线路的绝缘子串与导线在大风载荷作用下偏离其垂直位置,形成风偏角,并发生面外摇摆,在此过程中如果带电导体与铁塔之间的间隙过小(即风偏角过大),间隙的电气强度不能承受系统运行电压时就会发生放电,造成架空线路跳闸,即发生风偏闪络事故。架空线路风偏跳闸后重合闸成功率较低,严重影响和威胁电网系统的正常运行,造成巨大的经济损失与社会影响[1-3]。架空线路的风偏运动主要包括跳线风偏、导线相间风偏和绝缘子串风偏,根据文献[4]可知,国网公司所属的110 kV及以上架空线路发生风偏跳闸事故的主要原因是悬垂绝缘子串风偏导致的闪络放电,其占所有风偏故障的86.07%。为此,准确、高效地计算大风等极端工况下绝缘子串风偏角变化规律是架空线路防治风偏事故的首要工作,也是国内外研究架空线路风偏运动的重点内容。
国内外对架空线路绝缘子串风偏运动的传统计算研究主要集中在静力学分析方法[5-7],静力学分析方法将风压视为静态力,均匀作用在研究物体上,且认为绝缘子串风偏角在受力平衡时最大;LU等[8]针对实时监测系统,通过静力学分析方法提出了计算最小空气间隙的悬垂绝缘子串风偏运动三维模型;LONG等[9]从工程实际出发,应用静力学分析法讨论了风速、风压不均匀系数和风压高度变化系数等主要因素对于绝缘子串风偏角的影响,认为强风速对风偏角影响最为明显。作为传统风偏角计算方法,静力学分析方法具有计算简单和方便实用等特点,在架空线路工程设计中得到广泛应用,但由于其无法考虑架空线路风偏运动中明显的动态特性,不能准确计算绝缘子串风偏响应的变化规律,因而具有明显的局限性。为了能够更准确的计算架空线路绝缘子串风偏运动规律,国内外学者将包含脉动风的常规风载荷作为激励[10-12],采用有限元方法建立架空线路模型,分析绝缘子串的动态风偏响应[13-16]。MATHESON等[17]描述了一种孤立档架空线路在强风作用下的数值响应计算方法,通过基于快速傅里叶变换的“Monte Carlo”技术模拟风场,运用有限差分法进行数值求解,发现风载荷动态特性对架空线路风偏运动影响明显;LOREDO-SOUZA等[18]运用统计方法理论,比较风洞实验结果与理论计算结果,研究了架空线路在大风作用下的特性;刘小会等[19]基于随高度变化的Kaimal风速谱,运用谐波分析法模拟风场,并将其加载到500 kV超高压特征段线路的有限元模型上,分析线路结构安全度;楼文娟等[20]建立500 kV某实际线路的有限元模型,考虑气动阻尼对动态风偏响应影响,计算架空线路的风偏响应。有限元方法相较于传统静力学方法具有考虑全面、计算准确等优点,但其建立模型复杂且运算时间长、效率低,不便于在架空线路设计过程中推广和应用。
为了准确、高效地计算绝缘子串风偏响应规律,本文作者以连续档架空线路为研究对象,将绝缘子串视为质量均匀分布的刚性直杆,通过导线等效刚体模型考虑导线摆动对绝缘子串风偏运动的影响,建立大风工况下连续档架空线路动态风偏多刚体模型,通过Kaimal风速谱与Davenport相干函数模拟大风风场,结合工程实例分析计算架空线路绝缘子串的动态风偏响应特性,并与传统静力学方法和有限元方法进行对比分析,以便为架空线路动态风偏的设计、运行维护以及有效防治提供一条新途径。
1 架空线路动态风偏多刚体模型
1.1 架空线路风偏运动特征的刚体力学模型
选取1段有限连续档架空线路为研究对象,面对来流风方向,对此段线路铁塔从左至右进行1~n编号,其中1号塔和n号塔为耐张塔,其余为直线塔,绝缘子串编号与其所在塔同号,档距从左至右分别记为L1,L2,…,Ln-1。
以1号耐张塔上导线悬挂点为坐标原点建立坐标系,z为竖直方向,且向下为正;x为顺导线水平方向,方向指向n号塔为正;y为垂直导线水平方向,顺来流风方向为正。在不受风载荷的情况下,绝缘子串与导线在同一平面内,即xOz平面内。
结合工程上常用的复合悬垂绝缘子串芯棒特性,可以近似将绝缘子串看做1个质量均匀分布的刚性直杆,且在实际风偏运动中,悬垂绝缘子串顺导线方向(x方向)的位移相较其他方向位移,可以忽略不计,即可以认为悬垂绝缘子串的风偏运动只发生在yOz平面内。
在大风等极端工况下,架空线路发生面外风偏摆动,风偏均值位置由重力分量与平均风载荷分量共同确定。在实际风偏运动中,架空导线作为张紧索,风偏运动以导线所在平面的整体面外摆动为主,通过计算可知第i档架空导线在风偏均值附近面外摆动的固有频率p为
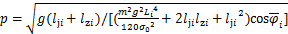 (1)
(1)
式中:m为导线单位长度质量;g为重力加速度;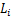 为导线档距;
为导线档距; 为导线运行张力;
为导线运行张力;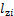 为第i档架空导线质心与导线挂点的垂向距离;
为第i档架空导线质心与导线挂点的垂向距离;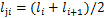 ,其中
,其中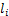 与
与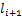 为第i档导线两侧绝缘子串长度;
为第i档导线两侧绝缘子串长度;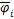 为第i档架空线路风偏角均值,由该档导线所受平均风载荷与重力载荷共同确定。
为第i档架空线路风偏角均值,由该档导线所受平均风载荷与重力载荷共同确定。
为考虑架空导线风偏运动对绝缘子串风偏摆动的影响,在架空导线风偏摆动固有频率相等的基础上,结合架空导线的风偏运动特征,考虑到架空导线在风偏运动中的轴向伸长量远远小于档距,一档架空导线可以等效为与导线挂点处的垂向距离为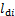 的质量均匀分布刚性直杆。
的质量均匀分布刚性直杆。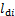 的表达式为
的表达式为
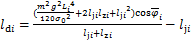 (2)
(2)
这样,把研究的架空输电线路段简化成由多个绝缘子串刚体和导线刚体组成的多刚体系统,如图1所示,并据此描述连续档架空线路的动态风偏现象,研究绝缘子串风偏角变化规律。
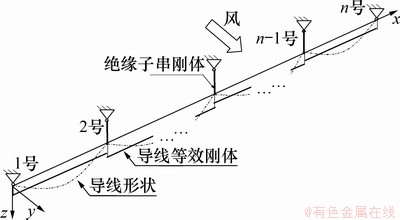
图1 架空线路多刚体模型
Fig. 1 Multi-rigid-body model of overhead lines
1.2 架空线路运动与来流风载荷
已知第i串悬垂串的长度为li,则在风偏运动的某一瞬时,架空线路中绝缘子串i的空间位置可由风偏角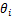 表示,此时,绝缘子串下端的位移在坐标轴的投影分别记为
表示,此时,绝缘子串下端的位移在坐标轴的投影分别记为 和
和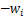 ,其中负号表示位移方向指向z轴的负方向,其表达式为:
,其中负号表示位移方向指向z轴的负方向,其表达式为:
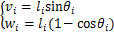 (3)
(3)
架空线路与来流风的耦合作用会产生气动阻尼,气动阻尼对架空线路风偏运动的影响远高于架空线路自身的结构阻尼,通过来流风与架空线路的相对运动,可以考虑气动阻尼对架空线路风偏运动的影响。
根据文献[21]计算公式,考虑架空线路与来流风的相对运动,第i串绝缘子串质心处的集中风载荷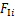 与第i档导线单位长度的风载荷
与第i档导线单位长度的风载荷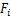 分别为:
分别为:
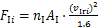 (4)
(4)
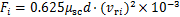 (5)
(5)
式中: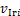 与
与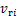 分别为来流风与绝缘子串质心和导线的相对风速;
分别为来流风与绝缘子串质心和导线的相对风速;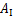 为单片绝缘子的迎风面积,m2;
为单片绝缘子的迎风面积,m2;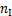 为绝缘子串中绝缘子的片数;μsc为架空线体型系数;d是架空线外径,mm。
为绝缘子串中绝缘子的片数;μsc为架空线体型系数;d是架空线外径,mm。
将绝缘子串与导线受到的风载荷向y轴与z轴方向进行分解。由于通常情况下导线悬挂高度处的湍流度较小,脉动风速与绝缘子串风偏运动速度远小于平均风速,故可将脉动风速与绝缘子串风偏运动速度的高次项与乘积项略去不计,可得绝缘子串与导线单位长度所受风载荷在y轴与z轴的分量为:
 (6)
(6)
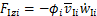 (7)
(7)
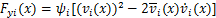 (8)
(8)
 (9)
(9)
式中: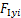 和
和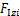 分别为第i串绝缘子串所受风载荷在y轴与z轴上的分量;
分别为第i串绝缘子串所受风载荷在y轴与z轴上的分量;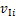 和
和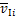 分别为绝缘子串质心处常规来流风速与平均风速;
分别为绝缘子串质心处常规来流风速与平均风速;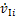 和
和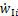 分别为绝缘子串质心处风偏运动速度在y轴与z轴上的分量;
分别为绝缘子串质心处风偏运动速度在y轴与z轴上的分量;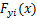 和
和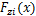 分别为第i档导线上距左端悬挂点x处微段所受风载荷在y轴与z轴上的分量;
分别为第i档导线上距左端悬挂点x处微段所受风载荷在y轴与z轴上的分量;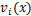 和
和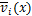 分别为此微段处的常规来流风速与平均风速;
分别为此微段处的常规来流风速与平均风速;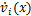 和
和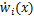 分别为此微段处的风偏运动速度在y轴与z轴上的分量;
分别为此微段处的风偏运动速度在y轴与z轴上的分量;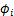 与
与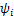 均为计算系数,其分别为
均为计算系数,其分别为
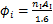 ,
, 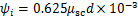
1.3 连续档架空线路多刚体动力学方程
运用分析力学方法,选取绝缘子串风偏角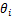 为系统广义坐标,建立架空线路绝缘子串动态风偏的连续档多刚体模型与计算方法。
为系统广义坐标,建立架空线路绝缘子串动态风偏的连续档多刚体模型与计算方法。
以静止时初始位置为重力势能原点,则第i串绝缘子串的重力势能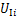 与第i档导线的重力势能
与第i档导线的重力势能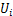 分别为:
分别为:
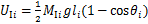 (10)
(10)
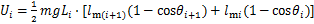 (11)
(11)
式中: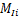 为第i串绝缘子串质量;
为第i串绝缘子串质量;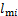 为导线等效刚体与第i串绝缘子串上端挂点的距离,其表达式为
为导线等效刚体与第i串绝缘子串上端挂点的距离,其表达式为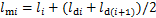 。
。
第i串绝缘子串的动能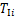 与第i档导线的动能
与第i档导线的动能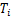 分别为
分别为
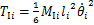 (12)
(12)
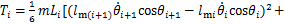
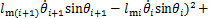
 (13)
(13)
在风偏运动的某一瞬时,令风偏角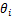 有虚位移
有虚位移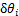 ,且
,且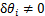 ,其余风偏角虚位移都为0,则此时第i串绝缘子串下端在y轴上的虚位移为
,其余风偏角虚位移都为0,则此时第i串绝缘子串下端在y轴上的虚位移为 ,在z轴上的虚位移为
,在z轴上的虚位移为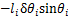 。
。
此时,在第i-1档导线上取距左端点距离为x的微段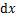 ,其在y轴与z轴方向上的虚位移分别记作
,其在y轴与z轴方向上的虚位移分别记作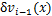 和
和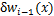 ,则风载荷对第i-1档导线做的虚功
,则风载荷对第i-1档导线做的虚功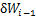 为
为
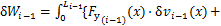
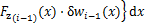 (14)
(14)
第i档导线上微段其在y轴与z轴方向上的虚位移分别记作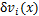 和
和 ,则风载荷对第i档导线做的虚功为
,则风载荷对第i档导线做的虚功为
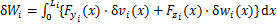 (15)
(15)
风载荷对第i串绝缘子串做的虚功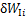 为
为
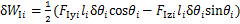 (16)
(16)
运用拉格朗日方程建立连续档架空线路的风偏运动方程,有
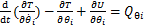 (17)
(17)
式中:T为架空线路多刚体模型系统的动能;U为系统的势能,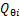 为广义非有势力,表达式为
为广义非有势力,表达式为
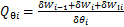 (18)
(18)
可得架空线路第i个绝缘子串的风偏运动方程为
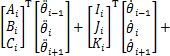
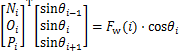 (19)
(19)
则对于整段连续档架空线路(1号,n号为耐张塔,即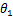 和
和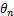 恒为0,其余为直线塔),其风偏运动方程为
恒为0,其余为直线塔),其风偏运动方程为
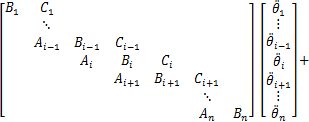
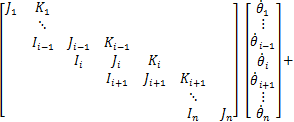
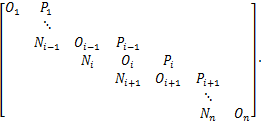
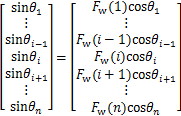 (20)
(20)
式中:
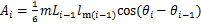 (21)
(21)
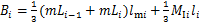 (22)
(22)
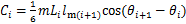 (23)
(23)

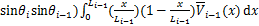 (24)
(24)
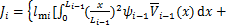
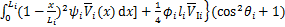 (25)
(25)
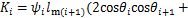
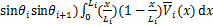 (26)
(26)
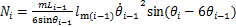 (27)
(27)
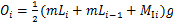 (28)
(28)
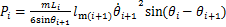 (29)
(29)
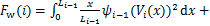
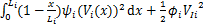 (30)
(30)
由式(19)和(20)可知:
架空线路第i个绝缘子串风偏运动受到与其相邻2个绝缘子串风偏运动的影响,方程的质量项、阻尼项和刚度项随风偏角而变化,风载荷与风偏角相互耦合产生的激扰力作为整个系统的外部激扰力,说明架空线路绝缘子串风偏运动具有非线性和随机性等特点。
连续档架空线路动态风偏多刚体模型的质量矩阵、阻尼矩阵、刚度矩阵为3个对角矩阵,风偏角初始位移与速度为0,一般认为耐张串和V型串的风偏角忽略不计,可以选取其作为计算的边界条件。
2 大风风场模拟与工程实例计算
2.1 五塔四线工程实例与大风风场模拟
以某段220 kV“五塔四线”架空线路为研究对象,此段架空线路两端铁塔为耐张塔(标记为1号和5号),中间有三基直线塔(标记为2号,3号和4号),档距分别为350,210,180和320 m,导线悬挂点距地面高度分别为21,30,33,31和25 m。已知标准高度10 m处的基准风速为25 m/s,风向与导线轴向夹角为90°,风向与水平面夹角为0°。悬垂绝缘子串为复合绝缘子串,型号为14片FXBW4-220/160-5,长度为2.97 m,质量为15.56 kg,导线型号为2×JL/G1A-630/45-45/7,单位质量为2.079 kg/m,初始张力为28 kN,多分裂导线的屏蔽作用暂不考虑。
采用随高度变化的Kaimal谱[22]和Davenport相干函数,求取回归系数矩阵,再构造正态随机过程与风速之间的互相关函数,对其进行Cholesky分解,进而采用AR模型综合得出脉动风速时程,将其加入平均风,完成大风风场模拟。
脉动风场模拟如图2所示,基准风速设为25 m/s,考虑到架空线路多在空旷田野和乡村等,故取B类地形粗糙度指数α=0.15,架空线路第1档与第4档各模拟6个风速样本,第2档与第4档各模拟5个风速样本,并将这22个风速样本顺x方向进行编号。图2(a)所示为模拟10 min内第6个风速样本处脉动风时程曲线;图2(b)所示为模拟风功率谱与目标谱比较;图3所示为风速样本的相关函数。
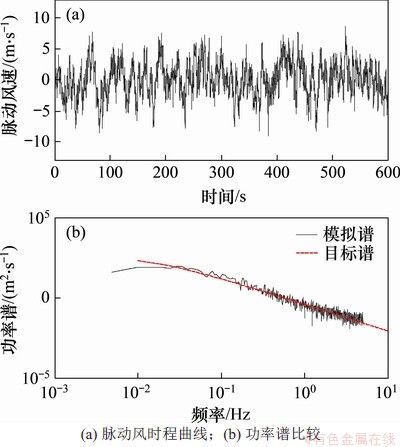
图2 脉动风风场模拟
Fig. 2 Simulation of fluctuating wind field
模拟风速谱与Kaimal风速谱(目标谱)吻合程度很高,证明风速模拟的正确性,且随着距离增加,2个风速样本之间相关性减弱,证明了空间风场模拟的正确性。为避免将大风直接作用到架空线路上会造成瞬时载荷,本文设定常规风风速由0增加到最大风速的用时为30 s,在此期间不添加脉动风,只有平均风;当风速稳定后,加入脉动风,研究架空线路风偏运动。
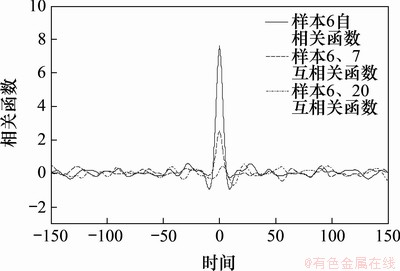
图3 风速样本的相关函数
Fig. 3 Correlation function of wind speed samples
2.2 架空线路绝缘子串动态风偏角计算
根据工程实例条件,将架空线路相关参数代入式(20)中进行计算。1号塔与5号塔的风偏角为边界条件,计算采用Newmark-β法,时间步长取0.01 s,风速稳定后各个风偏角时程曲线计算结果如图4所示。
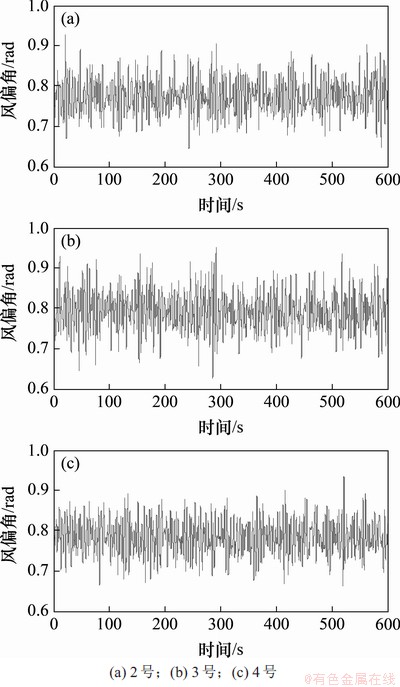
图4 风偏角运动时程曲线
Fig. 4 Time history curve of wind-induced deflection angle
由图4可知:架空线路悬垂绝缘子串在脉动风的作用下发生动态风偏运动,三基直线塔的悬垂串风偏角均值接近,分别为0.766,0.795和0.783 rad,最大风偏角出现在3号塔悬垂串风偏运动中,其值为0.95 rad。
通过风偏角运动的时程曲线估计此段架空线路各悬垂串风偏角运动幅值的概率密度,并进行对比分析,结果如图5所示。由图5可知:此段架空线路中各塔悬垂串的风偏角运动幅值出现在0.75~0.80 rad区间内的概率最大,2和4号塔悬垂串风偏幅值出现在0.65~0.75 rad区间内的概率大于3号塔悬垂串风偏幅值出现在该区间内的概率。而在0.85~0.95 rad区间内,3号塔悬垂串风偏幅值出现的概率明显大于其余悬垂串,说明在此段架空线路中3号塔更易发生风偏闪络事故,这是由于作为边界条件的耐张塔限制了相邻的2号和4号塔悬垂串的风偏运动。计算结果与事实相符,说明了运用多刚体模型计算连续档架空线路绝缘子串风偏角变化规律的有效性。
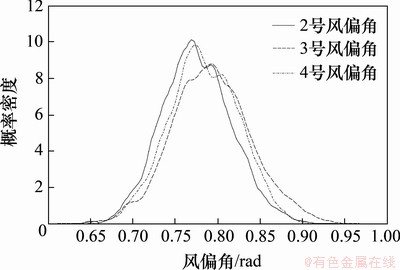
图5 绝缘子串风偏概率密度曲线
Fig. 5 Probability density curve of insulator string wind-induced deflection
3 不同计算方法的对比分析
3.1 架空线路模态振型的对比
运用有限元计算方法分析架空线路的动态风偏运动,绝缘子串与导线采用三维杆单元模拟,每档导线被划分为60个单元,通过迭代找形建立整段架空线路的有限元模型,施加脉动风荷载(如图6所示),采用瞬态动力学进行分析计算,得到架空线路的动态风偏运动结果。
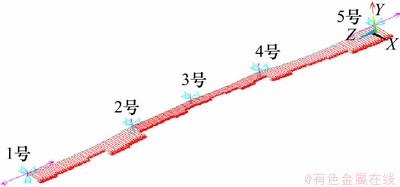
图6 有限元计算方法施加脉动风载荷示意图
Fig. 6 Diagram of fluctuating wind load applied by FEM
分别运用多刚体模型与有限元计算方法对2.1节工程实例中的连续档架空线路进行模态分析,绘制如图7所示的架空线路风偏响应各阶模态振型示意图。图7中x轴表示架空线路各个绝缘子串在沿导线方向的位置分布,y轴表示各个绝缘子串下端偏离架空线路初始位置的位移幅值比值。
由图7可见:多刚体模型与有限元计算方法得到的架空线路前3阶振型的形状基本一致,其幅值比分别为1.00:1.09:0.84,1.00:(-0.01):(-1.05),1.00:(-1.18):0.88,各阶模态频率分别为0.23,0.26和0.32 Hz,说明多刚体模型可以有效呈现架空线路各个绝缘子串在风偏运动中的相对位置变化。
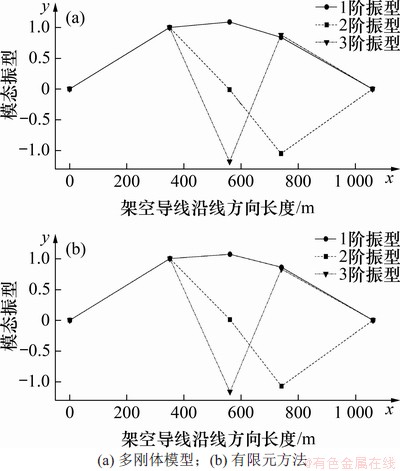
图7 架空线路风偏响应模态振型示意图
Fig. 7 Schematic diagram of mode shape of wind-induced deflection response of overhead lines
3.2 不同方法风偏响应结果对比
分别运用传统静力学方法与有限元方法计算2.1节工程实例,并将这2种方法计算得到的架空线路绝缘子串风偏响应结果与多刚体模型计算得到的结果进行比较,取工程设计中最为关注的风偏角均值与最大风偏角进行汇总,结果如表1所示,并以风速稳定后2号塔悬垂绝缘子串风偏角变化为例绘制多刚体模型与有限元方法计算得到的绝缘子串风偏角时程曲线对比图,如图8所示。
表1 3种计算方法风偏角结果对比
Table 1 Comparison of wind deflection angle results by three methods
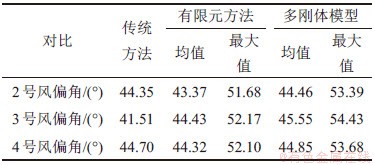
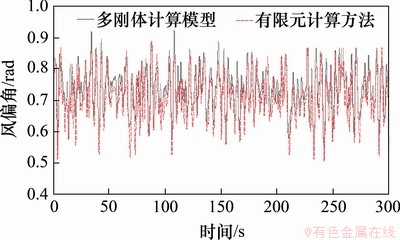
图8 2号塔绝缘子串风偏角时程曲线比较
Fig. 8 Comparison of time-history curves of wind deflection angle of insulator string in tower No.2
由表1可见:3种计算方法得到的2~4号绝缘子串风偏角均值差异率维持在2%附近,多刚体模型与有限元方法得到的绝缘子串最大风偏角差异率小于4%,满足工程精度要求,由此证明了连续档架空线路动态风偏多刚体模型的准确性。传统静力学方法由于自身局限性,无法计算绝缘子串动态风偏角的最大值,因而相较于传统静力学方法,多刚体模型使计算结果更准确。
由图8可见:多刚体模型与有限元方法得到的2号绝缘子串风偏角时程曲线吻合度较高,说明运用导线等效刚体风偏摆动模拟架空导线摆动对绝缘子串风偏响应的影响可以满足计算精度要求。虽然多刚体模型无法考虑导线的自身柔性,但通过与有限元方法对比可以发现导线自身柔性对绝缘子串风偏响应影响较小,多刚体模型可以展现绝缘子串风偏响应的动态变化规律。考虑到多刚体模型计算结果略大于有限元方法计算结果,所以在工程中可以将多刚体模型计算结果作为保守值使用,使设计更加安全。
为说明多刚体模型在计算效率方面优于有限元方法,以2.1节“五塔四线”架空线路为例,对比分析2种计算方法的运算效率。其中,测试所用的计算机硬件配置为CPU Core I5-9400F,RAM8Gb,建模软件平台分别为Matlab2011b和ANSYS14.0。运行结果显示,本文提出的多刚体模型计算用时为0.548 s,有限元模型计算用时为2 271.6 s。进一步验证测试,选择不同档数的架空线路为研究对象,施加600 s脉动风速时程进行计算,将2种方法计算不同档数架空线路风偏位移响应所使用的时间进行归纳比较,如图9所示。
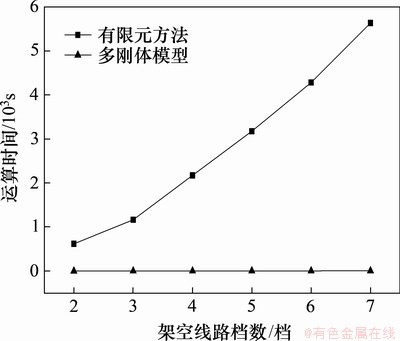
图9 2种计算方法运算时间比较
Fig. 9 Comparison of program running time between two methods
由图9可见:有限元方法运算时间长,且随着架空线路档数增加,运算时间增幅明显,这是由于有限元方法不仅建模过程复杂,还计算了许多附加量(如应力和应变等)。多刚体模型运算时间远低于有限元方法,证明了多刚体模型计算架空线路动态风偏位移的高效性。
4 结论
1) 提出一种用于计算连续档架空线路绝缘子串动态风偏响应的多刚体模型。
2) 模型计算结果与有限元方法计算结果基本一致,满足工程精度要求,验证了本文建立的多刚体模型的准确性,也说明了导线自身柔性对绝缘子串风偏角的变化规律影响较小。
3) 相较于传统静力学方法,多刚体模型能计算架空线路的动态风偏响应,相较于有限元方法,多刚体模型计算效率更高。
参考文献:
[1] 王璋奇, 陈海波, 周邢银. 垭口型微地形对输电线路风载荷影响的分析[J]. 华北电力大学学报(自然科学版), 2008, 35(4): 23-26.
WANG Zhangqi, CHEN Haibo, ZHOU Xingyin. Effects of yakou micro-relief on the wind loading formulation for transmission line design[J]. Journal of North China Electric Power University(Natural Science Edition), 2008, 35(4): 23-26.
[2] 蒋子丹, 蒋兴良, 蒋晏如, 等. 湖南地区输电线路悬式绝缘子自然积污规律[J]. 中南大学学报(自然科学版), 2018, 49(7): 1683-1690.
JIANG Zidan, JIANG Xingliang, JIANG Yanru, et al. Natural contamination characteristics of suspension insulator in Hunan Province[J]. Journal of Central South University(Science and Technology), 2018, 49(7): 1683-1690.
[3] 楼文娟, 罗罡, 杨晓辉, 等. 输电线路动态风偏响应特性及频域计算方法[J]. 高电压技术, 2017, 43(5): 1493-1499.
LOU Wenjuan, LUO Gang, YANG Xiaohui, et al. Response characteristics and frequency-domain calculation method of dynamic wind-induced deflection of transmission lines[J]. High Voltage Engineering, 2017, 43(5): 1493-1499.
[4] 李培栋, 汪亚平, 任妍, 等. 浅谈输电线路导线悬挂高度提高对风偏的影响[J]. 价值工程, 2010, 29(24): 220.
LI Peidong, WANG Yaping, REN Yan, et al. Simple analysis on impact of increasing the transmission line conduction wire suspending height on windage[J]. Value Engineering, 2010, 29(24): 220.
[5] 李孟春, 张艳玲, 杨北革, 等. 悬垂绝缘子串风偏最小间隙距离计算分析[J]. 电测与仪表, 2012, 49(3): 7-10.
LI Mengchun, ZHANG Yanling, YANG Beige, et al. Calculation and analysis of suspension insulator strings windage minimum air clearance[J]. Electrical Measurement & Instrumentation, 2012, 49(3): 7-10.
[6] CLAPP A L. Calculation of horizontal displacement of conductors under wind loading toward buildings and other supporting structures[J]. IEEE Transactions on Industry Applications, 1994, 30(2): 496-504.
[7] WANG Jian, XIONG Xiaofu, LI Zhe, et al. Wind forecast-based probabilistic early warning method of wind swing discharge for OHTLs[J]. IEEE Transactions on Power Delivery, 2016, 31(5): 2169-2178.
[8] LU Yongling, LIU Hao, HU Chengbo, et al. A three-dimensional real-time model for calculating minimum air clearance on wind deviation of overhead transmission line[C]// Proceedings of the 2nd International Conference on Power and Renewable Energy. Chengdu, China: ICPRE, 2017: 276-280.
[9] LONG Lihong, HU Yi, LI Jinglu, et al. Parameters for wind caused overhead transmission line swing and fault [C]// TENCON 2006 IEEE Region 10 Conference. Hong Kong, China. IEEE, 2006: 1-4.
[10] OWEN J S, ECCLES B J, CHOO B S, et al. The application of auto-regressive time series modelling for the time-frequency analysis of civil engineering structures[J]. Engineering Structures, 2001, 23(5): 521-536.
[11] GRIGORIU M. On the spectral representation method in simulation[J]. Probabilistic Engineering Mechanics, 1993, 8(2): 75-90.
[12] COSTA I C, VENTURINI L F, DA ROSA M A. Wind speed severity scale model applied to overhead line reliability simulation[J]. Electric Power Systems Research, 2019, 171: 240-250.
[13] 孙保强, 侯镭, 孟晓波, 等. 不同风速下导线风偏动力响应分析[J]. 高电压技术, 2010, 36(11): 2808-2813.
SUN Baoqiang, HOU Lei, MENG Xiaobo, et al. Characteristics analysis of conductors diaplacement under different wind speeds[J]. High Voltage Engineering, 2010, 36(11): 2808-2813.
[14] DAVENPORT A G. Gust response factors for transmission line loading[M]// Wind Engineering. Amsterdam, Netherlands: Elsevier, 1980: 899-909.
[15] 刘小会, 张路飞, 陈世民, 等. 连续档导线动刚度计算及模型简化[J]. 振动工程学报, 2016, 29(4): 720-729.
LIU Xiaohui, ZHANG Lufei, CHEN Shimin, et al. The calculation for dynamic stiffness and simplified model of continuous span conductors[J]. Journal of Vibration Engineering, 2016, 29(4): 720-729.
[16] 朱宽军, 徐鸿. 考虑风速时空分布特性的高压输电塔-线体系风致响应分析研究[J]. 中国电机工程学报, 2019, 39(8): 2348-2356.
ZHU Kuanjun, XU Hong. Analysis on wind-induced responses of high voltage tower-line system considering the spatial-temporal distribution characteristics of wind speed[J]. Proceedings of the CSEE, 2019, 39(8): 2348-2356.
[17] MATHESON M J, HOLMES J D. Simulation of the dynamic response of transmission lines in strong winds[J]. Engineering Structures, 1981, 3(2): 105-110.
[18] LOREDO-SOUZA A M, DAVENPORT A G. The effects of high winds on transmission lines[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1998, 74/75/76: 987-994.
[19] 刘小会, 严波, 林雪松, 等. 500 kV超高压输电线路风偏数值模拟研究[J]. 工程力学, 2009, 26(1): 244-249.
LIU Xiaohui, YAN Bo, LIN Xuesong, et al. Numerical simulation of windage yaw of 500 kV uhv transmission lines[J]. Engineering Mechanics, 2009, 26(1): 244-249.
[20] 楼文娟, 杨悦, 吕中宾, 等. 考虑气动阻尼效应的输电线路风偏动态分析方法[J]. 振动与冲击, 2015, 34(6): 24-29.
LOU Wenjuan, YANG Yue, LU Zhongbin, et al. Windage yaw dynamic analysis methods for transmission lines considering aerodynamic damping effect[J]. Journal of Vibration and Shock, 2015, 34(6): 24-29.
[21] 张殿生. 电力工程高压送电线路设计手册[M]. 2版. 北京: 中国电力出版社, 2003: 103-327.
ZHANG Diansheng. Design manual of high voltage transmission lines for electric engineering[M]. 2nd ed. Beijing: China Electric Power Press, 2003: 103-327.
[22] KAIMAL J C, WYNGAARD J C, IZUMI Y, et al. Spectral characteristics of surface-layer turbulence[J]. Quarterly Journal of the Royal Meteorological Society, 1972, 98(417): 563-589.
(编辑 秦明阳)
收稿日期: 2020 -03 -20; 修回日期: 2020 -05 -20
基金项目(Foundation item):国家自然科学基金资助项目(51608195);中央高校基本科研业务专项基金资助项目(2019QN130) (Project(51608195) supported by the National Natural Science Foundation of China; Project(2019QN130) supported by the Fundamental Research Funds for the Central Universities)
通信作者:王璋奇,博士,教授,从事输电线路工程基础理论和应用研究,E-mail:wangzq2093@163.com