基于灰色关联分析和多元非线性回归的内螺纹铜管污垢特性分析

陈健美^{1, 2}，李煜^{1, 2}，李玉强^{1, 2}

(1. 湖南省工程车辆底盘制造工程技术研究中心，湖南 长沙，410205；

2. 湖南涉外经济学院 机械工程学院，湖南 长沙，410205)

摘要：针对实验得到的相同工况下10根同内径的内螺纹铜管与1根铜光管的污垢情况，将污垢热阻比与螺纹数、螺距齿高比、相对粗糙度及螺旋角这4个几何参数进行灰色关联分析；以这些几何参数和污垢热阻比数据为变量参数，通过多元非线性回归，建立内螺纹铜管的污垢热阻模型；最后，依据该污垢热阻模型对内螺纹铜管污垢热阻的主要影响因素螺距齿高比进行机理分析。

关键词：内螺纹铜管；灰色关联分析；多元非线性回归；污垢热阻模型

中图分类号：TK124          文献标志码：A         文章编号：1672-7207(2013)08-3261-06

Fouling characteristic analysis on inner grooved copper tubes based on grey relational analysis and multiple nonlinear regression

CHEN Jianmei^{1, 2}, LI Yu^{1, 2}, LI Yuqiang^{1, 2}

(1. Research Center of Engineering Technology for Engineering Vehicle Chassis Manufacturing in Hunan Province,

Changsha 410205, China;

2. Department of Mechanical Engineering, Hunan International Economics University, Changsha 410205, China)

Abstract: The fouling states of ten inner grooved copper tubes and one plain copper tube under the same operating conditions were investigated by experiment. Subsequently, the fouling resistance ratio of the enhanced tube to the plain tube and four geometric parameters including the number of internal fin starts, ratio of axial element pitch to fin height, relative roughness and helix angle were introduced to take the grey relational analysis, and the multiple nonlinear regression was carried out according to the aforesaid variables’ data as well. Therefore, a fouling resistance model of inner grooved copper tubes was established. At last, the mechanism of the main factor influencing the fouling resistance of inner grooved copper tubes was analyzed on the basis of the model.

Key words: inner grooved copper tube; grey relational analysis; multiple nonlinear regression; fouling resistance model

Steinhagen等^[1]的调查表明，90%以上的换热设备均存在不同程度的污垢问题。换热设备污垢指换热面上妨碍传热和增加流体流过换热面时阻力的沉积物。杨善让等^[2]按成垢的理化过程将其分类为颗粒污垢、析晶污垢、混合污垢等7类。它通常是热的不良导体，换热面一旦有污垢，流体与换热面之间便形成附加传热热阻，称为污垢热阻。内螺纹铜管是用机械方法在管子内壁上加工出螺纹制成的铜质强化传热管^[3]，作为一种很好的强化传热元件，已在能源相关行业的换热设备上广泛应用，然而，该种强化管一旦运行在不洁净的工质中便会产生低导热性的污垢。Chen等^[4]对6根不同几何结构的内螺纹铜管与1根标准光管进行传热与阻力对比实验，发现同工况下螺纹管传热系数较光管传热系数均有大幅度提升，并提出了具有最佳传热特性的螺纹管几何结构。董志强等^[5]通过对比实验研究了6根不同齿形参数的内螺纹铜管的传热性能，发现齿形参数是内表面换热系数的主要影响因素，优化方向包括减小齿顶角、增加齿高、增大螺旋角、增加齿条数等。洪荣华等^[6]通过实验研究了7根内径为15.54 mm的美制内螺纹管的传热与阻力特性，拟合出该种强化管与若干几何参数相关的传热与阻力关系式。孙东亮等^[7]对内螺纹管层流状态下的流动与传热特性进行数值研究，发现螺旋角的增加能显著提高管的换热能力，螺纹牙数增加只能小幅度提高换热能力。以上研究均未考虑污垢条件下的工况，故其真实污垢特性有待研究。张巍等^[8-9]通过实验研究了7根内径为15.54 mm的美制内螺纹管的污垢特性，并基于传热传质类比法建立了管内的污垢分析模型。本文作者通过实验研究相同工况下10根内径为11.7 mm的国产内螺纹铜管与1根铜光管的污垢特性，将其污垢热阻比与螺纹数n、螺距齿高比p/e、相对粗糙度e/d及螺旋角β这4个几何参数进行了灰色关联分析；并以这些几何参数和污垢热阻比数据为变量参数，通过多元非线性回归，建立内螺纹铜管的污垢热阻模型；最后，依据该污垢热阻模型对内螺纹铜管污垢热阻的主要影响因素螺距齿高比p/e进行机理分析。

1  实验系统

1.1  实验管的材料及几何尺寸

表1所示为1根铜光管和10根内螺纹铜管(见图1)的几何参数及管内的混合污垢实验结果。内螺纹铜管的几何尺寸如图2所示。各管的管长L=2.22 m，内径d=11.70 mm(外径D=12.70 mm)，齿顶角α=41°，螺纹厚度t_t=0.20 mm，管内流体为pH=8.0的自来水，其污垢质量浓度为800 mg/L。

表1  内螺纹铜管的几何参数和实验数据

Table 1  Ranges of geometric parameters and test results (R_fp^*=3.2×10^{-5 m2}·K/W)

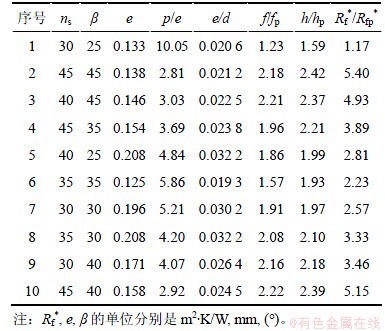
图1  内螺纹铜管

Fig. 1  Inner grooved copper tube

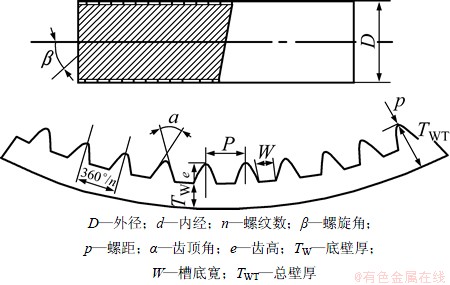
图2  内螺纹铜管的几何尺寸图

Fig. 2  Sketch of geometric dimensions for inner grooved copper tube

1.2  实验装置

实验装置如图3所示。循环工质在压差作用下从高位水箱流向低位水箱，途中经过试验管段与恒温水浴进行换热，经空冷换热器将工质冷却后再由水泵从低位水箱打到高位水箱，依次循环。每根管的壁温都有由3个T型热电偶来测量，管子的出口温度和入口温度用Pt100热电阻来测量，水浴温度用2个Pt100热电阻测量，用人工称质量法来测量流量信号；控制流速v为1.00 m/s，雷诺数Re为11 200左右，普朗特数Pr约为5.2，施密特数Sc约为0.2，循环水进出口压差通过差压计来测量。所有测量信号都经由传输电缆通过数据采集卡送入计算机进行储存和处理。由于采集过程中实验污垢热阻波动较大，较难得到非常精确的结果，故本文将实验末段的测得的污垢热阻R_f作为内螺纹铜管的污垢热阻R_f^*。该组内螺纹管的污垢热阻R_f^*均高于同材质同内径光管的热阻R_fp^*，且均可对其求得一个渐近污垢热阻。

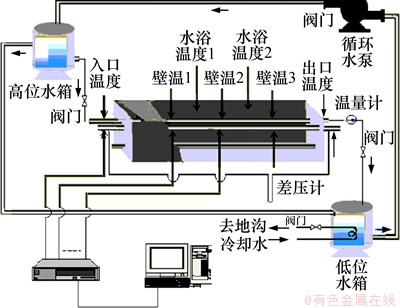
图3  实验仪器示意图

Fig. 3  Schematic diagram of experimental apparatus

1.3  实验原理

1.3.1  流动阻力系数f

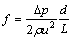               (1)

式中：Δp为实验段进出口的压差；ρ为流体的密度；u为流体的流速；d为实验管段的当量直径；L为实验管段长度。

1.3.2  管内换热平均表面传热系数

热流量Φ可由热平衡方程求得：

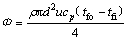           (2)

式中：t_fo和t_fi分别为流体出口和入口温度。单位时间内由管壁传递给工质的热量，可由牛顿冷却公式求得：

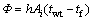             (3)

式中：t_f为流体的温度，是工质的特征温度，

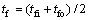             (4)

A_i和t_wt分别为总换热面积和水浴温度。联立式(2)和式(3)可得管内平均表面传热系数：

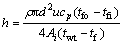          (5)

1.3.3  污垢热阻

污垢热阻的定义为

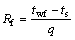                (6)

式中：t_wf为管壁与污垢之间的界面温度(由于管壁较薄，忽略其导热热阻时即为管外壁温度t_w，可以准确测定)；t_s为污垢与流体之间的界面温度(垢层表面温度)，

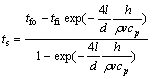          (7)

式(6)中的热流密度q可由流体能量平衡得到：

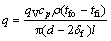             (8)

式中：q_V为体积流量；δ_f污垢厚度。δ_f通常要比d小很多，故δ_f可忽略不计。

这样，只要测量出所研究管段流体出入口温度、流量和管壁温度，应用上述关系即可确定对应的污垢热阻。

1.4  实验结果

利用上述实验系统装置对4个影响螺纹管污垢热阻的因素进行研究，它们是：螺纹数n、螺旋角β、螺距齿高比p/e及相对粗糙度e/d。实验结果见表1。

2  螺纹管与光管污垢热阻比的影响因素的灰色关联分析

2.1  实验结果标准化

考查的因素有螺纹数n、螺旋角β、螺距齿高比p/e及相对粗糙度e/d。这4个因素的量纲不一样，数据之间不具可比性，因此，需将实验结果进行标准化。其处理原理是利用灰色系统理论对非时间序列进行无量纲化处理，即指标区间化和归一化处理，公式为：

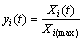              (9)

其中：i＝1，2，3，…，n；t=1，2，3，…，m；X_i(max)为每个序列里最大的变量值。

2.2  灰色关联分析

对1个参考数列X₀，有m个比较数列X₁，X₂，…，X_m，这m个比较数列与参考数列之间的关系可按下列公式计算：

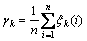               (10)

关联系数为

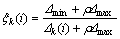            (11)

式中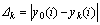：；i=1，2，3，…，n；k=1，2，3，…，m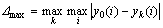；，即两级最大差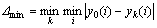；，即两级最小差；ρ为分辨系数，0＜ρ＜1，一般取0.5^[10-11]。

在本实验中，将污垢热阻比作为参考数列，螺纹数n、螺旋角β、螺距齿高比p/e和相对粗糙度e/d为比较数列，分别为X₁，X₂，X₃和X₄。将各序列X_i(t)(i=0，1，2，3，4)进行初值化处理，得到如下序列：

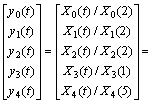
故

；

。

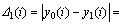
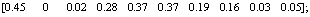
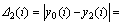
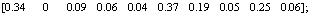
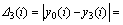
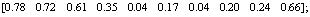
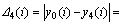
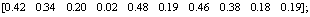
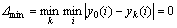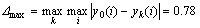然后，根据式(11)得X₁，X₂，X₃和X₄关于X₀的关联度矩阵：

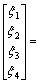
再据式(10)得关联度：

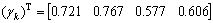      (12)

2.3  结果与分析

由式(12)可知：γ₃＜γ₄＜γ₁＜γ₂，于是，仅从关联度方面考虑，螺旋角β对螺纹管污垢热阻的影响最大，螺纹数n和相对粗糙度e/d对其影响次之，螺距齿高比p/e对其影响最小。

3  内螺纹铜管污垢热阻的多元非线性回归模型

假定内螺纹铜管与铜光管的污垢热阻比与螺旋角β、螺纹数n、相对粗糙度e/d和螺距齿高比p/e的函数关系式为

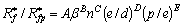      (13)

将式(13)左、右两边取自然对数，有

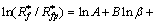
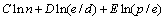       (14)

对表1中的几何参数和实验结果，以式(14)为数学模型，采用Origin8.0软件进行多元非线性回归，拟合得出：A=2.941 3，B=-0.004 1，C=-0.002 4，D=-0.003 1，E=-1.202 94。将以上各个系数代入式(14)，得：

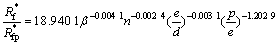(15)

经检验，上述回归模型的拟合优度达0.931 5，拟合较好。实测值与模型拟合值曲线如图3所示。R_f^*/R_fp^*实测值与模型值的相对误差见表2。从表2可见：实测值与拟合值相对误差均在±10%以内。

4  内螺纹铜管的结垢机理

由式(12)可知：内螺纹铜管管内混合污垢的主要影响因素是螺旋角β，似乎与式(15)矛盾，其实不然。原因在于螺旋角β、螺纹数n、相对粗糙度e/d和螺距齿高比p/e这4个影响因素之间存在如下函数关系：

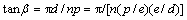       (16)

灰色关联分析只能从数据判断出影响因素序列与特征序列之间的关联度，而并不能表征。

各影响因素之间的关联度并不代表权重。从表1可知：由于相对粗糙度e/d很小，所以，螺旋角的变化最终导致螺距齿高比p/e出现较大波动，从而直接影响内螺纹铜管的渐近污垢热阻。因此，要研究内螺纹铜管的污垢形成机理还需借助于其污垢热阻模型即式(14)。

计算结果表明：螺旋角β、螺纹数n、相对粗糙度e/d对内螺纹铜管的渐近污垢热阻影响很小，几乎可以忽略，而螺距齿高比p/e对其影响显著。从表1可知：1号内螺纹铜管的螺距齿高比p/e最大，而渐近污垢热阻最小；2号内螺纹铜管的p/e最大，但渐近污垢热阻最大；其他各管的渐近污垢热阻也随p/e的增大而减小。顾维藻^[11]认为：流体流经螺纹肋时会在2根肋间表面y≤e区域内产生漩涡，其强度取决于螺纹肋的节距与高度比p/e。本文作者基于此认为：当螺距齿高比p/e较小时，缘于螺距偏小流体流经螺纹管齿时不能形成充分发展的漩涡，漩涡强度不够，且螺纹之间的二次扰流及再循环产生的顺流削弱了内螺纹铜管的壁面剪切应力(τ_s=0.5fu²，在此主要取决于沿程阻力系数f)，这削弱了沉积于管壁处和螺纹管齿处的污垢剥蚀作用，从而使得该强化管的渐近污垢热阻较大；随着p/e逐渐增大，管内流体先发生流动分离，壁面剪切应力增大，污垢剥蚀作用增强，渐近污垢热阻减小，继而重新到达换热表面，不过此时流体将不再获得后续管齿的继续扰动，传热效果也会有所削弱；随着p/e进一步增大，内螺纹铜管逐渐向铜光管过渡，几何参数对其传热传质的影响越来越小，从而渐近污垢热阻越来越趋向于铜光管的热阻，这便是1号内螺纹铜管与铜光管的渐近污垢热阻比接近于1的原因。因此，单从内螺纹铜管的抑垢方面考虑，其螺距齿高比p/e越大越好。然而，作为一种强化传热管，它必须在满足抑垢指标情况下，尽可能地使传热效果更好。根据工程实际中常用的评价强化传热性能指标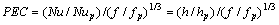：(其中Nu_p，f_p和h_p分别为铜光管的流体努谢尔特数、阻力系数和换热系数)，通过计算，得出在上述10根内螺纹铜管中，2号管的综合传热性能指标最好，见图4。当然，在工程实际中，由于内螺纹铜管的几何参数并不一定与上述10根的相同，所以，要根据其实际几何参数来确定其中综合传热性能指标最佳的强化管。

表2  R_f^*/R_fp^*实测值与模型值的相对误差

Table 2  Relative error of experimental and model-fitting R_f^*/R_fp^*

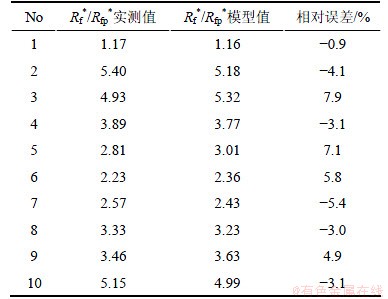
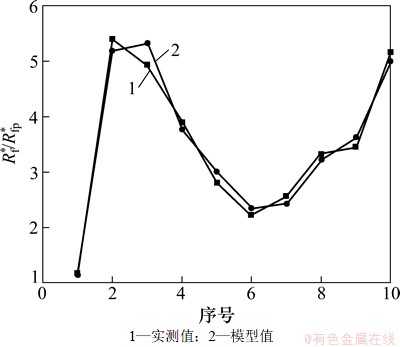
图4  R_f^*/R_fp^*实测值与模型值曲线

Fig. 4  Curves of experimental value and model-fitting value of R_f^*/R_fp^*

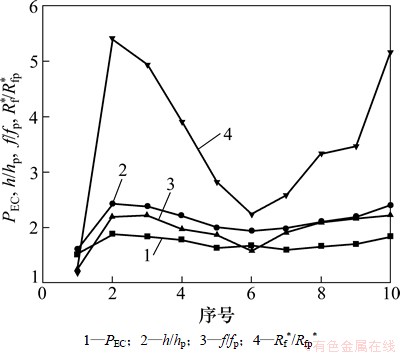
图5  各内螺纹铜管的4种指标

Fig. 5  Four indexes of inner grooved copper tubes

5  结论

(1) 影响内螺纹铜管污垢热阻的主要几何参数为螺距齿高比p/e，其渐近污垢热阻随p/e的增大而减小。

(2) 螺旋角β、螺纹数n和相对粗糙度e/d对内螺纹铜管污垢热阻的影响很小，且其影响主要是通过与螺距齿高比p/e的函数关系间接作用的。

(3) 内螺纹铜管的抑垢性能比光管的弱，但总体传热性能比光管的好。要获得最佳强化传热性能指标，需综合考虑管内传热传质2方面，选择最佳几何参数的内螺纹铜管。

参考文献：

[1] Steinhagen R, Steinhagen H M, Maani K. Problems and costs due to heat exchanger fouling in New Zealand industries[J]. Heat Transfer Engineering, 1993, 14(1): 28.

[2] 杨善让, 徐志明, 孙灵芳. 换热设备的污垢与对策[M]. 北京: 科学出版社, 2004: 15-38.

YANG Shanrang, XU Zhiming, SUN Lingfang. Heat exchanger fouling and countermeasures[M]. Beijing: Science Press, 2004: 15-38.

[3] 林宗虎, 汪军, 李瑞阳, 等. 强化传热技术[M]. 北京: 化学工业出版社, 2007: 4-25.

LIN Zonghu, WANG Jun, LI Ruiyang, et al. Heat transfer technologies[M]. Beijing: Chemical Industry Press, 2007: 4-25.

[4] CHEN Juin, Steinhagen H M, Duffy G G. Heat transfer enhancement in dimpled tubes[J]. Applied Thermal Engineering, 2001(21): 535-547.

[5] 董志强, 郭宏林, 蔡运亮, 等. 内螺纹铜管齿形参数对传热性能的影响[J]. 制冷与空调, 2009, 9(6): 35-38.

DONG Zhiqiang, GUO Honglin, CAI Yunliang, et al. Influence of tooth profile parameters of inner-grooved copper tube on heat transfer performance[J]. Refrigeration and Air-conditioning, 2009, 9(6): 35-38.

[6] 洪荣华, 钟昌雄, 倪煜, 等. 内螺纹强化管传热和阻力特性[J]. 工程热物理学报, 2008, 29(1): 154-156.

HONG Ronghua, ZHONG Changxiong, NI Yu, et al. The analysis of heat transfer and friction coefficients for internal thread tubes[J]. Journal of Engineering Thermo-physics, 2008, 29(1): 154-156.

[7] 孙东亮, 樊菊花, 王良璧. 内螺纹肋管内流动与传热的数值模拟[J]. 工程热物理学报, 2005, 26(3): 483-485.

SUN Dongliang, FAN Juhua, WANG Liangbi. Numerical study of fluid flow and heat transfer in helically ribbed tubes[J]. Journal of Engineering Thermo-physics, 2005, 26(3): 483-485.

[8] 张巍, 李冠球, 张政江, 等. 基于普朗特类比的螺纹管内污垢分析模型[J]. 中国电机工程学报, 2008, 28(35): 66-70.

ZHANG Wei, LI Guanqiu, ZHANG Zhengjiang, et al. Fouling model of internal helical-rib tubes based on Prandtle analogy[J]. Proceedings of the CSEE, 2008, 28(35): 66-70.

[9] 李冠球, 李蔚, 张政江, 等. 基于冯-卡门类比建立螺纹管内颗粒污垢模型[J]. 浙江大学学报: 工学版, 2010, 44(3): 495-498.

LI Guanqiu, LI Wei, ZHANG Zhengjiang, et al. Modeling particulate fouling in internal helical-rib tubes by Von-Karman analogy[J]. Journal of Zhejiang University: Engineering Science, 2010, 44(3): 495-498.

[10] 刘思峰, 郭天榜, 党耀国, 等. 灰色系统理论及其应用[M]. 北京: 科学出版社, 1999: 78-100.

LIU Sifeng, GUO Tianbang, DANG Yaoguo, et al. Grey system theory and its application[M]. Beijing: Science Press, 1999: 78-100.

[11] 顾维藻. 强化传热[M]. 北京: 科学出版社, 1990: 70-85.

GU Weizao. Enhanced heat transfer [M]. Beijing: Science Press, 1990: 70-85.

(编辑  陈灿华)

收稿日期：2012-06-08；修回日期：2012-08-24

基金项目：湖南省自然科学基金资助项目(11JJ3059)

通信作者：陈健美(1957-)，男，湖南望城人，博士，教授，从事工程车辆设计及优化研究工作；电话：0731-88118852；E-mail：jianmeich@163.com