DOI: 10.11817/j.issn.1672-7207.2019.04.026

裂隙对含孔洞砂岩力学及损伤演化特征的影响

周军华^{1, 2}，杨坤^{1, 2}，房凯^{1, 2}，赵同彬^{1, 2}，邱东卫^{1, 2}

(1. 山东科技大学 矿山灾害预防控制省部共建国家重点实验室培育基地，山东 青岛, 266590;

2. 山东科技大学 矿业与安全工程学院，山东 青岛, 266590)

摘要：为研究裂隙对含孔洞岩体力学及损伤演化特征影响，利用颗粒流模拟程序，对存在不同裂隙形态的含孔洞岩样在单轴压缩下的力学性质进行数值试验研究，分析岩样破裂与力学特征随裂隙形态的变化情况，对其损伤演化特性进行探讨。研究结果表明：裂隙的存在会改变原有含孔洞岩样沿孔洞贯通的破坏模式，大多数岩样会形成贯通裂隙的主破裂带；但当裂隙存在于距原主破裂带较远，且倾角较大或长度较小时，岩样依沿孔洞形成主破裂带；岩样的峰值应力随裂隙距孔洞距离或裂隙倾角的增大而增大，随裂隙长度的增大逐渐减小；含孔洞岩样周边存在距孔洞距离越远，长度越大的裂隙，在相同应变下损伤越小；含孔洞岩样的损伤修正系数取值为0.77 ~ 0.90。

关键词：孔洞；裂隙形态；岩石力学；声发射；损伤演化

中图分类号：TU45             文献标志码：A         文章编号：1672-7207(2019)04-0968-08

Effect of fissure on mechanical and damage evolution characteristics of sandstone containing hole defect

ZHOU Junhua^{1, 2}, YANG Kun^{1, 2}, FANG Kai^{1, 2}, ZHAO Tongbin^{1, 2}, QIU Dongwei^{1, 2}

(1. State Key Laboratory of Mining Disaster Prevention and Control Co-founded by Shandong Province and the

Ministry of Science and Technology, Shandong University of Science and Technology, Qingdao 266590, China;

2. College of Mining and Safety Engineering, Shandong University of Science and Technology, Qingdao 266590, China)

Abstract: In order to study the effect of fissure on the mechanics and damage evolution characteristics of rock containing hole defect, the mechanical behavior of sandstone containing hole defect with different fissure morphologies was tested under uniaxial compression conditions by using the particle flow simulation program. The fracture and mechanics characteristics of rock samples were analyzed with the changes of fissure morphology. The damage evolution characteristics of rock samples were discussed. The results show that the presence of fissures will change the fracture pattern of the original rock sample containing hole defect along the hole defect and most of the rock samples will form the main fractured by the fissure. For fissure that is relatively far away from the original main fracture belt and has a larger angle or a smaller length, the rock sample is still fractured along the hole defect. The peak stress increases with the increase of the distance from the fissure to the hole defect and it increases with the increase of the fissure angle. The peak stress of the rock sample gradually decreases with the increase of fissure length. For fissure that is further away from the hole defect and has greater length, the damage is smaller at the same strain. The damage correction coefficients are 0.77–0.90 for rock samples containing hole defect.

Key words: hole defect; fissure morphology; rock mechanics; acoustic emission; damage evolution

岩体内部存在的不同几何形态裂隙或孔洞等缺陷，使得岩体的结构和力学特征复杂，造成岩体被破坏与失稳。不同类型的缺陷之间相互作用对岩体力学及损伤演化特征有重要影响，对含孔洞岩体而言，周边裂隙的存在影响着岩体的力学及损伤演化特征，进而影响岩体的工程特性，因而系统研究裂隙对含孔洞砂岩力学机制、裂纹扩展特征的影响，分析2种缺陷同时存在条件下岩体内部裂纹的损伤演化特征，对于岩石工程的稳定性分析具有重大意义。目前，国内外许多学者对缺陷岩体的力学及损伤演化特征进行了大量研究^[1–4]。LEE等^[5–6]对预制裂隙的岩体进行单轴压缩试验，分析了缺陷几何对岩样强度和变形破坏特征的影响规律。LAJTAI等^[7–8]研究了压应力场下孔洞缺陷周边的破裂演化过程。WADLEY等^[9]通过大量试验发现声发射振铃计数更能反映材料内部损伤的演化过程。周喻等^[10]基于PFC程序，根据矩张量理论建立了细观尺度上岩石声发射模拟方法，结合室内岩石破裂全过程声发射特性试验，对比验证了颗粒流方法研究声发射模拟的可靠性。TANG等^[11–12]建立了单轴应力状态下岩石基于声发射的损伤模型，得出了煤岩的损伤演化曲线和方程。LI等^[13–15]的研究表明，岩体力学参数及声发射特征显著受孔洞裂隙等缺陷分布的影响。大量研究表明，声发射是研究岩体失稳损伤演化过程的重要手段，砂岩变形破裂过程中的裂纹扩展及声发射特征显著，因此，对含孔洞砂岩的力学及损伤演化研究具有重要意义，而目前人们针对含孔洞砂岩中裂隙存在的几何形态对其力学及损伤演化特征的影响分析较少。为此，本文作者采用颗粒流软件PFC数值模拟构建不同裂隙几何形态的含孔洞红砂岩试样模型，研究在单轴压缩下裂隙形态对含孔洞岩样破裂和力学特征的影响规律，并基于声发射特征和应变等效原理，利用损伤修正系数对损伤本构模型进行修正，探讨含孔洞岩样的损伤演化规律。

1  含孔洞红砂岩数值模型

CUNDALL等^[16]在离散元法的基础上创建了颗粒流理论，该理论适合从细观层次上分析材料的损伤演化破断机制及大变形过程。PFC模型的岩石能够重现真实岩石样本中观察到的许多行为特征，例如应力–应变响应、开裂和破裂模式。岩石的声发射与岩石内部微破纹的产生直接相关，PFC模型中1个链接断裂会产生1次应变能的释放，即发生了1次声发射，通过统计颗粒链接断裂数即可模拟岩石声发射事件^[17]。在模拟颗粒黏结破坏过程中，PFC程序利用设置黏结模型来表征颗粒之间胶结物的存在，本文采用平行黏结模型来对砂岩进行模拟及细观参数的标定^[18]，最终细观物理力学参数见表1。利用表1中参数计算得岩样颗粒流模型与室内试验的力学特性，见表2和图1。从表2和图1可以看出：两者力学特性基本一致，表明其选取较合理并可用于后续的计算分析。

表1  红砂岩细观物理力学参数

Table 1  Physico-mechanical parameters of red sandstone

表2  完整砂岩试样试验和模拟力学参数对比

Table 2  Comparison of mechanical parameters by test and simulation

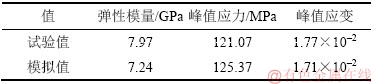
图 1  试样破裂模式对比

Fig. 1  Comparison of sample fracture mode

为了分析裂隙几何形态对含孔洞砂岩力学特征和损伤破坏声发射特征规律的影响，建立了同室内标准岩石尺寸一致(直径×长度为50 mm×100 mm)的完整岩石模型，共生成1 0773个颗粒。通过预制直径d为10 mm、圆心偏离试样中心下10 mm的孔洞，和长度为2a、宽度为2 mm、倾角为α、中心点距孔洞距离为h的裂隙，来构建含孔洞砂岩试样模型见图2，图中σ₁为轴向加载。模拟11种工况，见表3。模拟加载过程采用位移加载方式，加载速率为0.05 m/s。

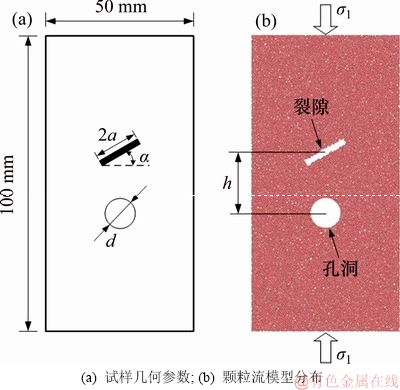
图 2  试样孔洞裂隙参数分布

Fig. 2  Geometric of hole and fissure in sample

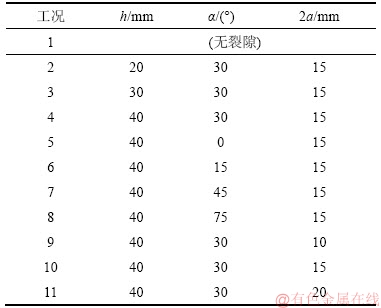
表 3  模拟试验工况

Table 3  Simulation test conditions

2  试验结果及分析

2.1  砂岩试样破裂特征

图3所示为单轴压缩下不同裂隙距孔洞距离h含孔洞红砂岩试样的破裂模式。图3中数字N表示为主贯裂带裂纹的扩展顺序，数字N^#表示为非主裂纹的扩展顺序。由图3可知：裂隙的存在会改变原有含孔洞试样的裂纹扩展和破裂特征。无裂隙岩样，在孔洞上下边缘萌生初始裂纹1和1^#，继续加载新生裂纹2萌生并迅速扩展，最终与裂纹1贯通破裂。在相同裂隙长度下，裂隙距孔洞距离h=20 mm岩样为裂隙尖端萌生出的翼裂纹1与倾斜次生裂纹2，和共面次生裂纹3与4交叉贯通破裂；h=30 mm岩样由裂隙尖端萌生出共面次生裂纹1与2扩展贯通破裂；h=40 mm的含孔洞岩样，在裂隙尖端萌生出翼裂纹1与倾斜次生裂纹2，该裂纹与预制裂隙相垂直，随后裂纹迅速扩展贯通破裂。含孔洞岩样在破裂过程中预制裂隙与孔洞之间的微裂纹N^#的扩展对岩样的破坏并未起到关键作用，这意味着裂隙的存在会改变原有含孔洞试样沿孔洞贯通破坏的破坏模式，大多数试样会形成贯通裂隙的主破裂带。

图4所示为不同裂隙倾角α砂岩试样的破裂模式。由图4可知：随着倾角α的增大，岩样的破裂模式变化可分为2类，即α为0°，15°和45°岩样为裂隙尖端发育的翼裂纹与倾斜次生裂纹贯通破裂，以及α=75°岩样为预制裂隙左侧产生的远场倾斜裂纹1与孔洞周边区域产生的拉伸裂纹2贯通破裂，岩样破裂时在孔洞边缘产生拉伸裂纹1^#，方向近似与轴向加载方向平行。这表明含孔洞岩体周边裂隙的存在不一定改变原有的主贯通破裂带，例如当含孔洞岩样周边存在距原主贯通破裂带较远、倾角较大的裂隙时，岩样依然沿孔洞形成主贯通破裂带。

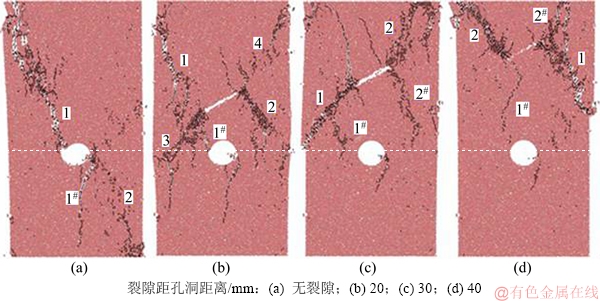
图 3  不同裂隙距孔洞距离的砂岩破裂模式

Fig. 3  Fracture modes of sandstone with different fissure distances from hole defect

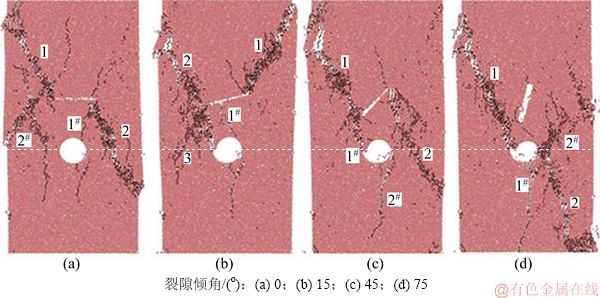
图 4  不同裂隙倾角的砂岩破裂模式

Fig. 4  Fracture modes of sandstone with different fissure angles

图5所示为不同裂隙长度2a砂岩试样的破裂模式。由图5可知：在相同裂隙倾角下，当2a=10 mm时，孔洞上下边缘萌生初始裂纹1，2和3，多条裂纹的扩展与贯通导致了岩样失稳破坏，裂隙的存在基本未影响岩样破裂模式，岩样以孔洞为主贯通破裂带；当2a为15 mm和20 mm时，岩样的裂纹扩展特征发生改变，由裂隙尖端萌生出的翼裂纹与次生裂纹扩展贯通破裂，未与孔洞之间出现贯通。这表明当含孔洞岩样周边存在距原主贯通破裂带较远、长度较小的裂隙时，岩样依然沿孔洞形成主贯通破裂带。

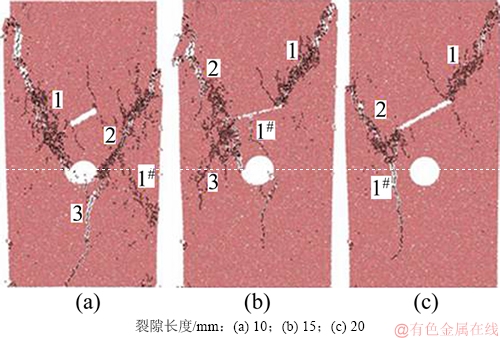
图 5  不同裂隙长度的砂岩破裂模式

Fig. 5  Fracture modes of sandstone with different fissure lengths

2.2  砂岩试样力学特征

图6所示为不同裂隙形态的含孔洞红砂岩试样应力–应变曲线，具体力学参数见表4。由图6(a)可知：含孔洞砂岩试样周边裂隙的存在降低了岩样的力学参数；在相同裂隙长度下，裂隙距上边缘距离h=20 mm(105.09 MPa)，h=30 mm(105.85 MPa)和h=40 mm (110.98 MPa)的岩样与无裂隙岩样峰值应力112.20 MPa相比，分别降低5.8%，5.7%和1.1%；裂隙与孔洞的距离对含孔洞岩样峰值应力和峰值应变影响不大，峰值应力随h的增大而增大的变化规律，h=40 mm的岩样峰值应力比h=20 mm的岩样峰值应力提高5.6%，这说明含孔洞岩样裂隙距孔洞距离越远，承载能力越强。

由图6(b)可知：岩样的峰值应力随裂隙倾角α几乎呈线性上升趋势，α=75°(112.64 MPa)岩样的峰值应力比α=0°(102.44 MPa)岩样的峰值应力提高9.7 %。

由图6(c)可知：裂隙长度2a对含孔洞岩样的力学参数影响显著，在相同裂隙倾角下，随着2a从10 mm增大到20 mm，岩样的峰值应力由112.80 MPa减小到90.66 MPa，降低约20.0%；峰值应变由1.67 mm减小到1.52 mm，降低9.0%。这说明随着裂隙长度的增大，岩样的峰值应力和峰值应变均呈逐渐减小的趋势。

3  岩体声发射及损伤演化特征分析

3.1  声发射特征分析

图7所示为部分裂隙形态下含孔洞红砂岩试样应力–应变–声发射(AE)特征关系曲线。从图7可知声发射演化过程大致分为3个阶段：第1阶段为声发射初始阶段，该阶段对应于应力–应变曲线的弹性阶段，声发射活动次数稀少，甚至为零，这种现象不同于真实岩体，真实岩体在初始阶段声发射活动缓慢增加，这因为PFC平行黏结模型没有初始损伤，真实岩体内部或多或少具有一定的初始损伤；第2阶段为声发射递增阶段，该阶段对应于岩石的塑性阶段，声发射信号急剧增加直到峰值；第3阶段为声发射递减阶段，该阶段对应于岩石的损伤阶段，声发射信号不断降低，直至平稳或为零。缺陷岩样可能会出现2~3次声发射振铃计数高峰，应力在峰后降低到一定程度有反弹现象，分析原因主要在于该岩样的破裂模式，裂隙尖端萌发的裂纹与孔洞贯通破裂，使岩样达到峰值强度，但岩样未完全贯通，继续加载岩样产生新的贯通破裂带时出现新的高峰应力，随后应力下降。裂隙形态对含孔洞砂岩声发射特征的影响主要体现在声发射信号强度与对应的应变上。

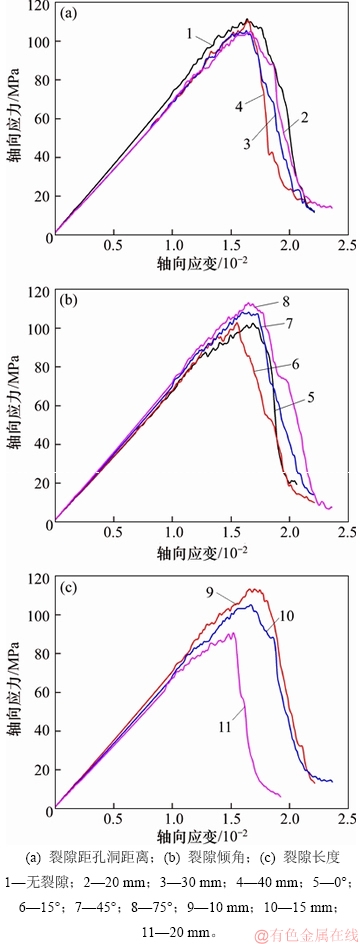
图 6  不同裂隙形态岩样应力-应变曲线

Fig. 6  Stress–strain curves of rock samples with different fissure morphologies

表 4  含孔洞砂岩力学参数汇总表

Table 4  Mechanical parameters of sandstone containing hole defect

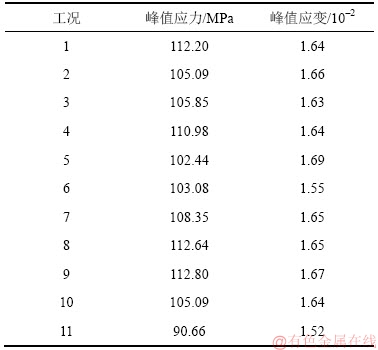
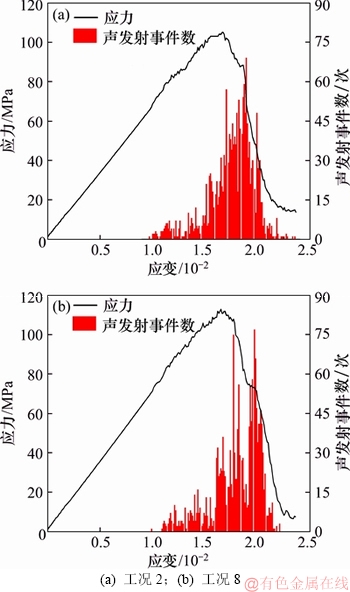
图 7  含孔洞砂岩应力–应变–声发射特征变关系曲线

Fig. 7  Stress–strain–AE relationship of sandstone containing hole defect

3.2  损伤演化特征分析

大量研究表明，声发射振铃计数与材料位错、断裂和裂纹扩展所释放的应变能成比例，能很好地反映材料性能的变化^[19]。KACHANOV^[20]定义了损伤变量D，假设无损的截面面积A完全失去承载力时累计声发射振铃计数为N，断面损伤面积为A_m时累计声发射振铃计数为N_m，岩石内部的损伤变量D为

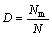                  (1)

由于砂岩试样在模拟压缩过程中很难达到完全破坏，引入了损伤修正系数D_u这一参数，得修正公式^[9]为

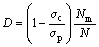             (2)

式中：σ_c为残余强度；σ_p为峰值强度。

基于声发射特性和应变等效原理^[21]，建立了单轴压缩条件下砂岩试样的损伤本构模型为^[12]

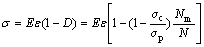     (3)

式中：σ为应力；ε为应变；E为弹性模量。

本文以声发射振铃计数为特征参数来描述砂岩的损伤演化特性，利用声发射特征的损伤本构模型方程拟合的应力–应变曲线如图8所示。从图8可知：拟合曲线与实际数值曲线相差不大，说明运用基于声发射参量的砂岩损伤模型来描述砂岩的破裂损伤过程是可行的。

根据式(2)所定义的损伤变量得出红砂岩试样在工况2下的砂岩单轴加载破坏过程损伤演化如图9所示。由图9可知：在加载初期砂岩内部几乎不产生损伤，岩样处于压密的弹性变形过程；随着荷载增加，微损伤出现局部集中化趋势，损伤逐渐在岩样破坏部位集聚，形成宏观裂纹；继续加载岩样新生裂纹萌发，随后形成明显的裂纹扩张方向和演化形态，表明岩样内的微裂纹迅速扩展、汇合，局部出现宏观破坏，此时岩样的承载性能迅速下降，损伤变量急剧上升；之后进入损伤平稳阶段，微裂纹的衍生和扩展逐渐趋于稳定，岩样失去承载能力。

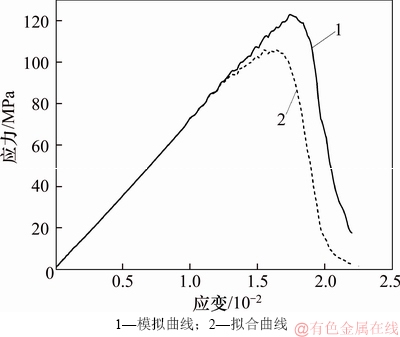
图 8  砂岩理论应力-应变曲线与模拟曲线对比

Fig. 8  Comparison of theoretical stress–strain curve with simulation of sandstone

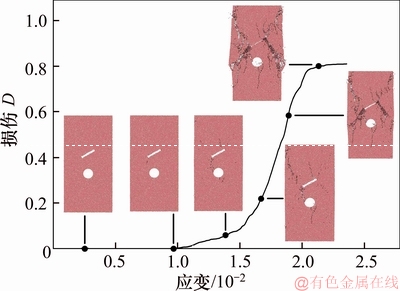
图 9  含孔洞砂岩单轴加载损伤演化过程

Fig. 9  Damage evolution process of sandstone containing hole under uniaxial compressive load defect

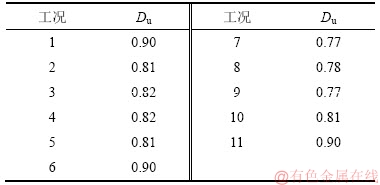
图10所示为不同裂隙形态含孔洞岩体红砂岩试样的应变与损伤关系曲线，由图10可知：裂隙几何形态主要影响含孔洞岩体损伤演化过程中的损伤平稳阶段及对应的应变。相同裂隙长度的含孔洞砂岩裂隙距孔洞距离h越远，在同应变下岩样损伤越小；对于不同的裂隙倾角α，D_u也不同，例如裂隙倾角为15°时D_u约为0.90，而裂隙倾角为45°时D_u约为0.77；相同裂隙倾角的含孔洞砂岩裂隙长度2a越大，在同应变下，岩样损伤越小。表5所示为含孔洞砂岩的损伤修正系数D_u。从表5可以看出：不同裂隙几何形态的含孔洞岩样存在不同的D_u，D_u取值为0.77~0.90。

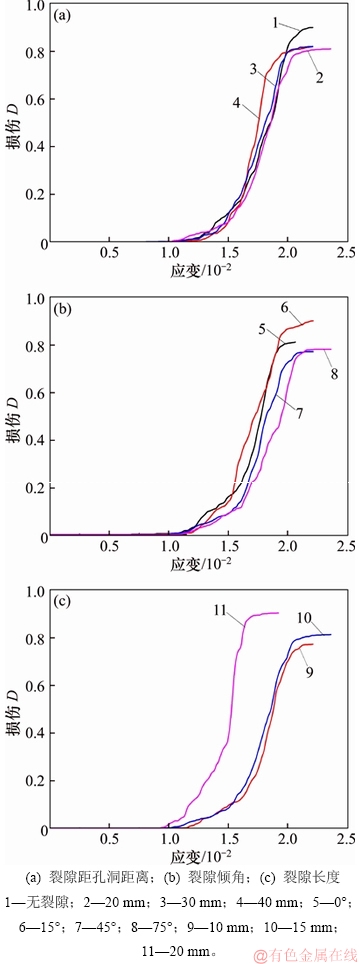
图 10  含孔洞砂岩应变-损伤变量曲线

Fig. 10  Strain–damage curves of sandstone containing hole defect

表 5  含孔洞砂岩损伤修正系数

Table 5  Damage correction coefficients of sandstone containing hole defect

4  结论

1) 裂隙的存在会改变原有含孔洞试样沿孔洞贯通破坏的破坏模式，大多数试样会形成贯通裂隙的主破裂带。孔洞上下边缘萌生初始裂纹，多条裂纹的扩展与贯通导致岩样失稳破坏，这表明当含孔洞岩样周边存在距原主贯通破裂带较远，且倾角较大或长度较小的裂隙时，岩样依然沿孔洞形成主贯通破裂带。

2) 含孔洞砂岩试样周边裂隙的存在降低了岩样的力学参数。岩样的峰值应力随裂隙距孔洞距离h的增大而增大的变化规律，随裂隙倾角α几乎呈线性上升趋势；在相同裂隙倾角下，随着裂隙长度2a的增大，岩样的峰值应力和峰值应变均逐渐减小，例如长度为20 mm岩样的峰值应力比长度为10 mm岩样的峰值应力降低20%左右。

3) 声发射信息反映了砂岩内部的损伤破坏情况，与其内部原生缺陷的压密，新生裂纹的萌发、扩展及贯通等演化过程密切相关。含孔洞岩体的声发射演化过程分为声发射初始阶段、声发射递增阶段和声发射递减阶段3个阶段。

4) 损伤本构模型引入损伤修正系数D_u后的拟合曲线与实际数值曲线相差不大，说明修正后的损伤本构方程能更好地模拟砂岩损伤演化过程。裂隙形态主要影响含孔洞岩体损伤演化过程中的损伤平稳阶段及对应的应变，含孔洞砂岩周边存在距孔洞距离越远，长度越大的裂隙，在同应变下岩样损伤越小；不同裂隙形态的含孔洞岩样存在不同的损伤修正系数D_u，D_u取值为0.77~0.90。

参考文献：

[1] CHEN Minliang, JING Hongwen, MA Xiujun, et al. Fracture evolution characteristics of sandstone containing double fissures and a single circular hole under uniaxial compression[J]. International Journal of Mining Science and Technology, 2017, 27(3): 499-505.

[2] 刘学伟, 刘泉声, 陈元, 等. 裂隙形式对岩体强度特征及破坏模式影响的试验研究[J]. 岩土力学, 2015, 36(S2): 208-214.

LIU Xuewei, LIU Quansheng, CHEN Yuan, et al. Experimental study of effects of fracture type on strength characteristics and failure modes of fractured rock mass[J]. Rock and Soil Mechanics, 2015, 36(S2): 208-214.

[3] YANG Shengqi, HUANG Yanhua, JING Hongwen, et al. Discrete element modeling on fracture coalescence behavior of red sandstone containing two unparallel fissures[J]. Engineering Geology, 2014, 178(6): 28-48.

[4] YANG Shengqi, JING Hongwen, XU Tao. Mechanical behavior and failure analysis of brittle sandstone specimens containing combined flaws under uniaxial compression[J]. Journal of Central South University, 2014, 21(5): 2059-2073.

[5] LEE H, JEON S. An experimental and numerical study of fracture coalescence in pre-cracked specimens under uniaxial compression[J]. International Journal of Solids & Structures, 2011, 48(6): 979-999.

[6] YANG S Q, DAI Y H, HAN L J, et al. Experimental study on mechanical behavior of brittle marble samples containing different flaws under uniaxial compression[J]. Engineering Fracture Mechanics, 2009, 76(12): 1833-1845.

[7] LAJTAI E Z, LAJTAI V N. The collapse of cavities[J]. International Journal of Rock Mechanics & Mining Sciences & Geomechanics Abstracts, 1975, 12(4): 81-86.

[8] WANG Xiao, TIAN Longgang. Mechanical and crack evolution characteristics of coal–rock under different fracture-hole conditions: a numerical study based on particle flow code[J]. Environmental Earth Sciences, 2018, 77(8): 297.

[9] WADLEY H N G, SCRUBY C B, SPEAKE J H. Acoustic emission for physical examination of metals[J]. Metallurgical Reviews, 2013, 25(1): 41-64.

[10] 周喻, 吴顺川, 许学良,等. 岩石破裂过程中声发射特性的颗粒流分析[J]. 岩石力学与工程学报, 2013, 32(5): 951-959.

ZHOU Yu, WU Shunchuan, XU Xueliang, et al. Particle flow analysis of acoustic emission characteristics during rock failure process[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(5): 951-959.

[11] TANG Chunan, XU Xiaohe. Evolution and propagation of material defects and Kaiser effect function[J]. Journal of Seismological Research, 1990, 13(2): 203-313.

[12] 刘保县, 黄敬林, 王泽云, 等. 单轴压缩煤岩损伤演化及声发射特性研究[J]. 岩石力学与工程学报, 2009, 28(S1): 3234-3238.

LIU Baoxian, HUANG Jinglin, WANG Zeyun, et al. Study on damage evolution and acoustic emission character of coal-rock under uniaxial compression[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(S1): 3234-3238.

[13] LI Yinping, CHEN Longzhu, WANG Yuanhan. Experimental research on pre-cracked marble under compression[J]. International Journal of Solids & Structures, 2005, 42(9): 2505-2516.

[14] ZHAO Xingdong, ZHANG Hongxun, ZHU Wancheng. Fracture evolution around pre-existing cylindrical cavities in brittle rocks under uniaxial compression[J]. Transactions of Nonferrous Metals Society of China, 2014, 24(3): 806-815.

[15] YANG Shengqi, JING Hongwen. Strength failure and crack coalescence behavior of brittle sandstone samples containing a single fissure under uniaxial compression[J]. International Journal of Fracture, 2011, 168(2): 227-250.

[16] CUNDALL P A, STRACK O D. A discreate numerical model for granula assemblies[J]. Geotechnique, 1979, 29(1): 47–65.

[17] 王云飞, 黄正均, 崔芳. 煤岩破坏过程的细观力学损伤演化机制[J]. 煤炭学报, 2014, 39(12): 2390-2396.

WANG Yunfei, HUANG Zhengjun, CUI Fang. Damage evolution mechanism in the failure process of coal rock based on mesomechanics[J]. Journal of China Coal Society, 2014, 39(12): 2390-2396.

[18] 尹延春, 赵同彬, 谭云亮, 等. 基于Otsu图像处理的岩石细观模型重构及数值试验[J]. 岩土力学, 2015, 36(9): 2532-2540.

YIN Yanchun, ZHAO Tongbin, TAN Yunliang, et al. Reconstruction and numerical test of the mesoscopic model of rock based on Otsu digital image processing[J]. Rock and Soil Mechanics, 2015, 36(9): 2532-2540.

[19] 刘学文, 林吉中, 袁祖贻. 应用声发射技术评价材料疲劳损伤的研究[J]. 中国铁道科学, 1997, 18(4): 74-81.

LIU Xuewen, LIN Jizhong, YUAN Zuyi. Research on evaluation of material fatigue damage by acoustic emission technology[J]. China Railway Science, 1997, 18(4): 74-81.

[20] KACHANOV L M. Rupture time under creep conditions[J]. International Journal of Fracture, 1999, 97(1/2/3/4): 11–18.

[21] LEMAITRE J, SERMAGE J P, DESMORAT R. A two scale damage concept applied to fatigue[J]. International Journal of fracture, 1999, 97(1): 67-81.

(编辑  杨幼平)

收稿日期：2018-05-31；修回日期：2018-08-14

基金项目(Foundation item)：中国博士后科学基金资助项目 (2016M590644) (Project (2016MS90644) supported by China Postdoctoral Science Foundation of China)

通信作者：房凯，博士，讲师，从事岩石力学研究；E-mail：fk861018@163.com