J. Cent. South Univ. (2020) 27: 256-266

DOI: https://doi.org/10.1007/s11771-020-4293-2

Failure of circular shaft subjected to hydraulic uplift:Field and numerical investigation

ZHAO Guo-qing(赵国庆)¹, YANG Yu-you(杨宇友)², MENG Su-yun(孟素云)¹

1. School of Civil Engineering, Shenyang Jianzhu University, Shenyang 110168, China;

2. School of Engineering and Technology, China University of Geosciences Beijing, Beijing 100083, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020

Abstract: A working shaft for pipe-jacking is going to be excavated into a sand stratum with high hydraulic pressure in Guangzhou, China. A newly assembled pre-stressed retaining system has been proposed to support the shaft for its efficiency, safety and sustainability. Full-scale field tests and numerical analysis were conducted to analyze the base failure of the circular shaft with confined water. The failure process of the shaft was observed on site. The construction process of step-by-step excavation of shaft and layer-by-layer assembly of pre-stressed structure was simulated in detail. Simulation results agree well with the phenomenon on site. The base failure modes present that tensile damage generates at the center of the base due to non-uniform uplift and shear failure occurs along the soil-structure interface. The effects of shaft size and confined water head were also discussed. As a result, a critical ratio of diameter to shaft depth is put forward to assess the size effect of circular shaft. A conclusion that the soil strength should be partially considered in anti-inrushing safety factor calculation is drawn by analysis and comparison of various calculation methods. This research provides a reference for the base stability evaluation of similar shaft subjected to hydraulic uplift.

Key words: circular shaft; field test; finite element analysis; base stability; water inrush

Cite this article as: ZHAO Guo-qing, YANG Yu-you, MENG Su-yun. Failure of circular shaft subjected to hydraulic uplift: Field and numerical investigation [J]. Journal of Central South University, 2020, 27(1): 256-266. DOI: https://doi.org/10.1007/s11771-020-4293-2.

1 Introduction

With large-scale infrastructure construction, the number of working shafts for pipe-jacking or maintenance of municipal pipelines has been increasing in recent decades [1]. The shafts constructed in clay strata underlain with sub-aquifers are frequently encountered in coastal cities [2-4]. The shafts are generally circular and shallow. Even so, the construction of a shaft controlled in the strata with high artesian pressure is affected by the issue of stability. Base stability of shafts subjected to hydraulic uplift is important to engineering safety [5-8].

The design approach of excavation subjected to hydraulic uplift in codes mainly adopts the pressure balance method (PBM) [9, 10]. This method defines that hydraulic failure by uplift occurs when pore-water pressure under a low permeability ground layer becomes larger than the mean overburden pressure. The case records reported by scholars indicate that PBM is too conservative due to ignoring the strength of soil [11, 12]. Some modified methods for estimating the basal failure caused by hydraulic uplift are put forward. Modified PBM with an eye to the strength of the stratum. LIU and LIU [13] supposed that the shear strength along clay-wall interface is fully mobilized. YANG and ZHENG [14] presented that the shear strength of the surrounding side of the overburden and the cohesion of the bottom contact surface should be considered. ZHANG et al [15] pointed out that the cohesion of the aquitard inside excavation should be multiplied by a reduction coefficient of 0.3-0.6. SUN [16] suggested the cohesion and the internal friction angle should be reduced with a coefficient of 0.4-1. In addition, some experiments and simulations have also been carried out to study the failure process. HONG and NG [5] report that the artesian pressure required to initiate uplift inside the excavation is about 1.2 times bigger than the overburden pressure of the clay on the basis of centrifuge tests and FEM back- analysis. DING et al [17] established a numerical model to analyze the plastic deformation failure of excavation. HONG et al [18] found that the dominant failure mode changes from simple shear in narrow excavations to combined modes in wide excavations, and the contribution of mobilized undrain shear strength to ultimate hydraulic uplift resistance is no more than 13%. WANG et al [19] proposed four stages of water inrush in excavation bottom: continuous deformation, progressive deformation, shear failure, and water inrush and sinking stages. Based on the experimental results and experience in practice, SUN [16] presented two types of basal failure by uplift: local failure (including sand piping around the container–soil interface and sand boiling on the surface of the aquitard) and general upheave. The researches focusing on the rectangular excavation and the failure mechanisms are still controversial. Moreover, the judgment method and mechanisms of circular shaft failure induced by hydraulic uplift need to be understood.

Considering the rise of circular working shafts involving base failure problem in urbanization construction and the deficiencies in understanding failure mechanism and evaluating safety factor, the objectives of this paper are 1) to analyze the failure mechanisms of circular shafts subjected to hydraulic uplift; 2) to study the effects of diameter and confined water head on failure by uplift; and 3) to determine a reasonable stability judgment method for circular shaft subjected to hydraulic uplift. To address these objectives, a full scale in-situ test was conducted in Guangzhou, China. The water inrush failure of shafts during the test process has been observed. Besides, finite element method (FEM) was employed to simulate the excavation and supporting process. The measured and computed results were interpreted and compared. Parametric study was also carried out to analyze the influence factors of failure by hydraulic uplift.

2 Full-scale field test

2.1 Site condition

The test shaft is in the east of East Yanjiang Rd Zengcheng District Guangzhou, China. The linear distance between Zengjiang river and the shaft is about 70 m. The north and east of the site is banana field, and the south is benchland (see Figure 1). The test shaft is circular of flat shape with a diameter of 4.2 m.

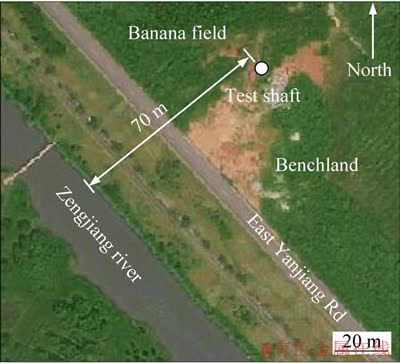
Figure 1 Field test satellite imagery

The soil character is obtained according to geological drilling, combining with field identification, standard penetration test and laboratory soil test. Figure 2 shows geotechnical profile and soil properties in situ. The top-down distribution of soil layers is as follows: artificial filling, silty clay, and medium sand.

Figure 3 illustrates the uplift stability diagram of the shaft subjected to hydraulic uplift on site. A layer of water-bearing medium sand with a head of water, h_w, exists at a depth, D, below the bottom of the circular shaft in silty clay of diameter, d. The confined water table is about 0.5 m under surface.

Figure 2 Geotechnical profile and soil properties in situ (γ_l: bulk density; c: cohesion; φ: friction angle; e₀: void ratio; E: compression modulus; SPT N: blow numbers of standard penetration test; k: permeability coefficient)

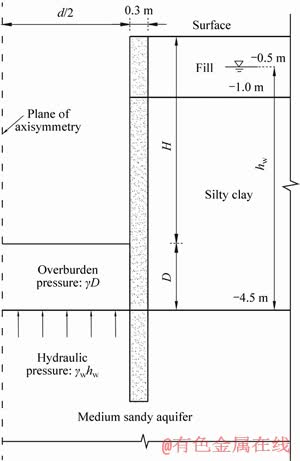
Figure 3 Shaft uplift stability diagram on site

2.2 Groundwater controlling and retaining scheme

The test shaft took high pressure jet grouting pile as waterproof wall to control groundwater. The pile was about 6 m in depth, 0.5 m in diameter, 0.115 m in lap joint width along the circular direction, 0.3 m in valid thickness along the radial direction. The diameter of the shaft is 4.2 m (see Figure 3).

The shaft was retained by a new assembly steel structure that is proposed by YANG et al [20] and GUAN et al [21], but some improvements of it are done in this paper. As shown in Figure 4, the improved retaining structure unit consists of a steel plate and a steel pipe with two holes on both ends, which are welded together through steel block. The structure form changes spiral to single layer, and the connecting steel pipes are replaced by pre-tightening components. The pre-tightening components can apply radial pressure in inhibitting soil deformation [22].

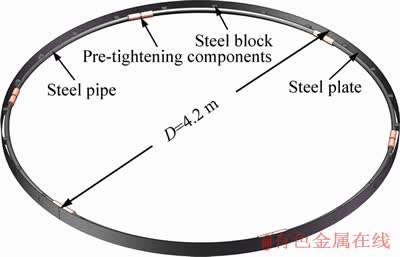
Figure 4 Single layer retaining structure

2.3 Construction procedure

The overall construction sequence is as follows:

Step 1: A circular route was set out with a diameter of 4.2 m.

Step 2: A jet grouting pile was constructed to form a closed waterproof curtain.

Step 3: Excavated a circular trough with a depth of 0.4 m following the setting-out route, then, the retaining structure was assembled from top to bottom and layer by layer. Repeated the excavation and support till supporting reaches 3.2 m underground. A total of 16 layers of structure was assembled.

Step 4: Water inrush suddenly happened at the bottom of the shaft when the excavation went down to 3.6 m underground. The water inflow capacity increased gradually.

Step 5: The shaft was backfilled with soil, and the test ended.

3 Simulation method

3.1 Establishment of model

3.1.1 Model mesh and boundary conditions

The finite element software PLAXIS 2D 2015 [23] was used for numerical analysis on the field test construction process. An axisymmetric two- dimensional finite element model was established in accordance with the circular shaft character on site. As shown in Figure 5, the numerical model of the excavation was extended to 10 m both in horizontal direction and in vertical direction. Each lateral boundary horizontal deformation was fixed, the bottom was fixed too, and the top was free. The left side adopted impermeable boundary owing to symmetry. The right side submitted to permeable boundary. The bottom was impermeable boundary.

3.1.2 Constitutive model and model parameters

Hardening soil model with small-strain stiffness (HSS) is an advanced elastic-plastic model supported in PLAXIS, which has been verified that it is suitable for simulating the excavation [24-28].

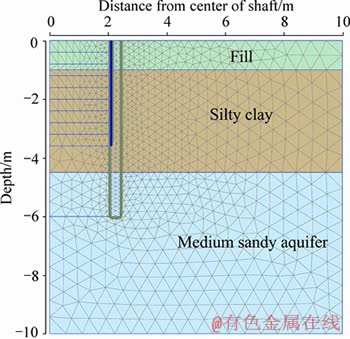
Figure 5 Numerical model of test shaft

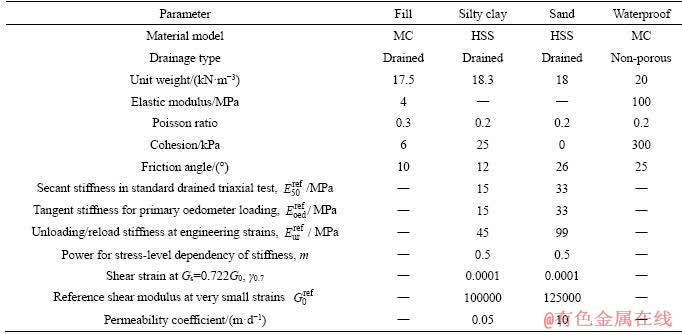
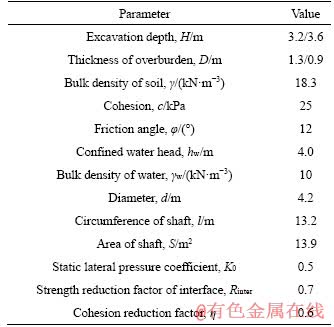
In the numerical simulation, the HSS model was used for describing the stress-strain behavior of silty clay and sand strata, while the waterproof wall was modeled as Mohr-Coulomb (MC) materials. Soil stiffness and strength parameters were determined, based on field investigation and laboratory test. Small-strain stiffness parameters were selected according to the PLAXIS manual [23]. Calculation parameters of the soil layers and the waterproof wall are listed in Table 1. Due to the disturbance of the clay caused by waterproof wall construction, the strength of soil at the interface of soil and waterproof wall (soil-wall interface) was reduced by 0.7 on the basis of adjacent soil.

Table 1 Calculation parameters of soil layers and waterproof wall

The steel plate of the structure is discontinuous in the circular direction which can not transfer axial force and bending moment. The steel pipe is the main bearing member, which could be assembled as a continuous integral pipe. According to the principle of equivalent stiffness, the stiffness of the steel pipe was transferred into plate. The equivalent plate was simulated by plate element in PLAXIS that can bear pulling, pressing, bending and shearing. The interface element was adopted between structure and soil. Parameters of steel support are as follows: the density of steel was 7800 kg/m³, the axial stiffness was 6.3×10⁵ kN/m, the flexural rigidity was 480 kN·m²/m, Poisson ratio was 0.3.

3.2 Construction process simulation

The analysis process relies on the field construction sequence. The calculation phases are listed below:

Phase 1: Calculated initial equilibrium stress field according to K0 procedure with the confined water table of -0.5 m.

Phase 2: Activated of jet grouting piles and the interface.

Phase 3: Reset displacements to zero, and excavated to -0.4 m.

Phase 4: Excavated to -0.8 m, in the meantime, activated the last layer retaining structure and interface. When excavating below the confined water table, set the excavation bottom as the seepage boundary.

Phase 5: Repeated Phase 4 to execute excavation and retaining according to excavating 0.4 m of each step. Till calculation can not be convergent.

4 Test and computed results

4.1 Observed process of water inrush on site

The test shaft began to be excavated and was dug to 3.2 m below the surface on March 17, 2015. The monitoring results showed that there was no obvious ground deformation and no water flow into the shaft. Still no water was found at the bottom after a night in this state.

On March 18, 2015, some upward seepage containing sand was observed at the soil-wall interface at the bottom when excavated to 3.6 m underground (see Figure 6). However, the base of the shaft was stable. Water levels in the shaft were maintained at the level of the base by pumping from shallow sump. However, the water inrush was found near the center of the shaft after a few hours, and then several other water inrush points were later observed. The water inrush developed where the clay had apparently cracked, and the water inflow increased gradually.

Figure 6 Water inrush at bottom of circular shaft on site

4.2 Validation of computed results

Figure 7 shows the computed water inrush process of the shaft. The numerical calculation was convergent until the excavation went to 3.2 m underground. The shaft had been stable. The maximum displacement was 3 mm.

The FE software showed that the soil body seems to collapse when the excavation reached 3.6 m below the surface. The location of the maximum incremental displacement changed from the center of the shaft to the soil-wall interface when the excavation depth varies from 3.2 m to 3.6 m (see Figure 7(a)). It implied that the displacement persistently increased at the soil-wall interface at this moment. As shown in Figure 7(b), the failure points cut through the soil-wall interface, which illustrated that the soil reached the limit of the destruction at the interface. The directions of the principal stresses were about 45° relative to the horizontal and vertical direction near the interface. This indicated that soil generated shear failure. Figure 7(c) illustrates that the flow becomes bigger as it gets closer to the interface. Thus, it might be concluded that water inrush appeared for the first time at the soil-wall surface when the excavation gets as deeper as 3.6 m.

Figure 7(d) shows the total horizontal strain of the aquitard at the bottom. The major tension strain generated at the lower part from the center of the aquitard. The cracks would extend to the bottom of the shaft as time goes on. Finally, water inrush would occur at the center of bottom. The water inrush process obtained by numerical results is consistent with the phenomenon observed on site.

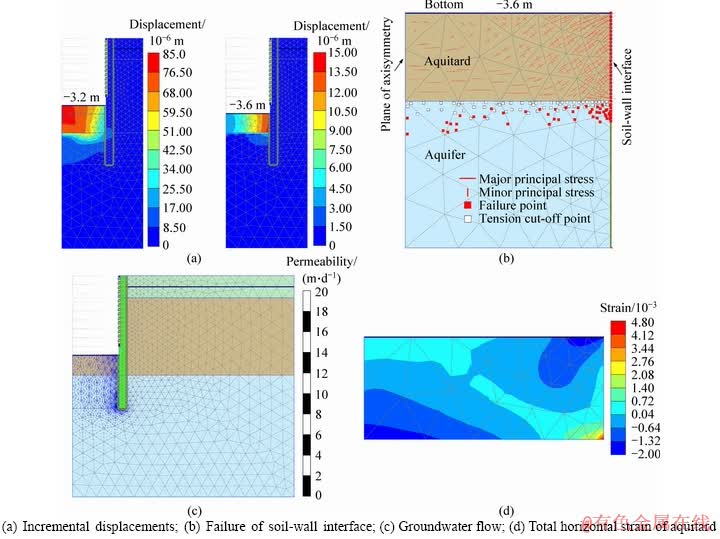
Figure 7 Computed water inrush process of shaft:

4.3 Failure mechanisms

Figure 8 shows the deformation mechanism of the shaft before failure. Volumetric strain mainly occurred on the top surface of the water-bearing sand stratum below the bottom (see Figure 8(a)). Major shear strain was also observed at the same location (see Figure 8(b)). The maximum strain appeared at the center of the shaft and gradually decreased with the increase of the distance. It can be concluded that the sand was suspended on the top surface with the action of hydraulic uplift, which was controlled by volumetric strain. As shown in Figure 8(b), the maximum shear strain occurred on the soil-wall interface on the surface of the bottom and gradually decreased with the increase of the distance. It implies that the aquitard resisting to hydraulic uplift mainly depends on the shear strength of the soil on the soil-wall interface.

Figure 9 shows the uplift and shear failure of the aquitard at the bottom of the shaft when the excavation reached -3.6 m. The volumetric strain cut through the whole interface of the aquitard and the confined aquifer, and gradually decreased from the center to the edge (see Figure 9(a)). The non-uniform uplift generated at the aquitard with the action of artesian pressure. Figure 9(b) shows the mobilized shear strength of the soil. The mobilized shear strength on the soil-wall interface was larger than that in other regions of the aquitard. It shows that the strength of the soil contributed to resisting hydraulic uplift. The soil generated shear failure on the soil-wall interface is shown in the previous analysis in Figure 7(b). Thus, the aquitard fails in tensile damage due to non-uniform uplift and shear failure on the soil-wall interface.

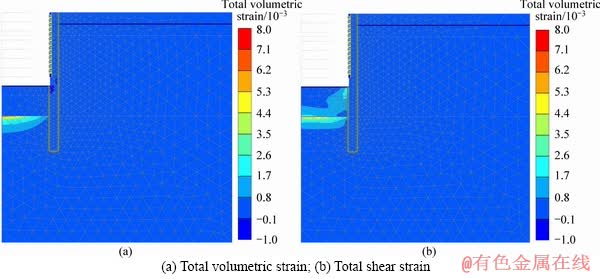
Figure 8 Deformation mechanism of shaft before failure:

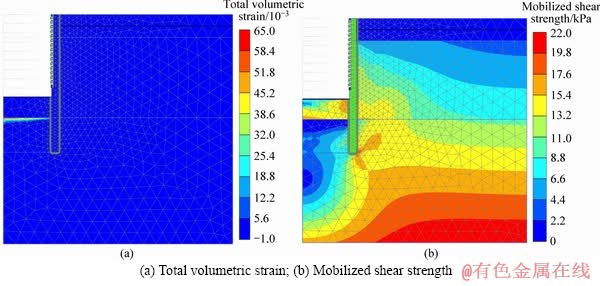
Figure 9 Uplift and shear failure of aquitard at bottom of shaft:

5 Discussion

5.1 Shaft size and artesian pressure affected to uplift stability

A numerical parametric study was conducted to obtain the critical thickness of overburden, D_c, with different diameters, d, and various confined water heads, h_w. The calculation results are illustrated in Figure 10. The numerical calculation ended with the calculation non-convergence. The thickness of the overburden at previous construction phase before non-convergence is defined as critical thickness of the overburden. The critical thickness of the overburden plus the excavation depth of the shaft, H, is constant (see Figure 3). The expression of normalized critical overburden pressure is the same as the formula of the anti-inrushing safety factor in codes [9, 10].

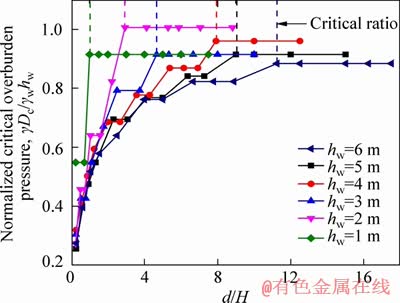
Figure 10 Computed critical thickness of overburden in response to diameter of shaft

The normalized critical overburden pressure shows the capacity of the overburden pressure of the clay inside the shaft (γD_c) resisting to artesian pressure (γ_wh_w). As shown in Figure 10, all values of the normalized critical overburden pressure are equal to or less than 1. According to the definition of the critical thickness of overburden, all working conditions of the shaft adopted in Figure 10 should be stable, which means the anti-inrushing safety factor should be equal to or greater than 1. It indicates that there are some other factors contributing to the anti-inrushing stability except the overburden pressure. The codes’ design approach of excavation subjected to hydraulic uplift is too conservative that only considers the overburden pressure.

As shown in Figure 10, as d/H<1.0, the normalized critical overburden pressure was less than 0.55 and almost showed a linear increase with d/H. It shows that the overburden pressure contributes less than 55% to the anti-inrushing stability, as d/H<1.0. As d/H was between 1.0 and critical ratio, the anti-inrushing effect of the overburden pressure improved gradually with the increase of d/H. As d/H was greater than the critical ratio, the normalized critical pressure was nearly invariable. A different confined water head implied a different critical ratio. It can be concluded that the size effect of the shaft is the most obvious as d/H<1.0. It gradually weakens with the increase of d/H, and nearly disappears when d/H grows greater than critical ratio.

As d/H was greater than the critical ratio, the size effect of the shaft disappeared and the normalized critical overburden pressure was less than 1 (see Figure 10). However, the shaft still maintained stability. With the previous mechanism analysis, it can be concluded that the strength of the clay inside the shaft also played a crucial role in resisting hydraulic uplift.

As illustrated in Figure 11, the critical ratio of the diameter to the shaft depth was approximately linear with the confined water head. The higher the confined water head was, the larger the critical ratio would become. The relationship of the critical ratio and the confined water head has been established by means of the least square method. The equation provides a solution for obtaining the critical ratio.

5.2 Theoretical water inrush calculation methods

Table 2 shows the comparison of the anti- inrushing safety factors obtained by five theoretical methods, FEM, and field test. As illustrated, in current design guidelines worldwide [9, 10], the hydraulic pressure required to initiate base instability is simply assumed to be equal to the overburden pressure of the clay inside the excavation. The different mobilization degrees of the soil strength are adopted in the formulas of three modified methods. LIU and LIU [13] assumes that the shear strength of clay is fully mobilized on the soil-wall interface. YANG and ZHENG [14] take the effect of the cohesion at the bottom of the clay into account. ZHANG et al [15] introduce a cohesion reduction factor on the basis of YANG and ZHENG [14]. SUN [16] proposes that the shear strength should be reduced due to the defect of soil-wall interface.

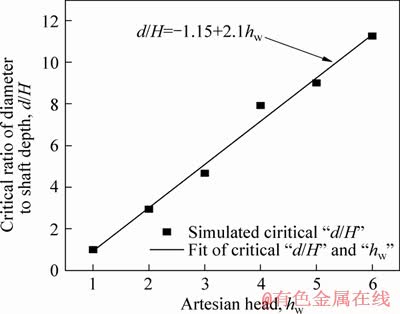
Figure 11 Critical ratio of d/H at different confined water head

As shown in Table 2, based on the site condition, the anti-inrushing safety factor was calculated by different methods at an excavation depth of 3.2 m (where the base was stable) and 3.6 m (where water inrush was observed) underground, respectively. Table 3 illustrates the parameters and values that would be used in calculating. By comparing the safety factor values, a tentative conclusion can be drawn that the PBM is over-conservative, the method considering the cohesion at the bottom of the clay is rather unsafe, and the downward shear stress along the soil-wall interface should be partially considered based on the degree of the disturbance of the soil.

6 Conclusions

In this paper, full-scale field tests and numerical analyses were conducted to study the failure mechanism of the circular shaft subjected to hydraulic uplift. The anti-inrushing safety factors obtained by five theoretical methods were discussed. The following conclusions are drawn:

Table 2 Comparison of anti-inrushing safety factors obtained by different theoretical methods, FEM, and field test at an excavation depth of 3.2 m and 3.6 m underground, respectively

Table 3 Parameters adopted in Table 2

1) The finite element analysis results are in good agreement with the observed phenomena on site, implying that the present FEM model can be used for stability evaluation of similar shaft subjected to hydraulic uplift.

2) The failure mode of the soil is obtained when the water inrush occurs. The sand is suspended on the top surface of the artesian aquifer with the action of the artesian pressure. The aquitard fails in tensile damage due to non-uniform uplift along the radial and shear failure on the soil-wall interface.

3) The size effect of the shaft is the most obvious, and contributes much to the anti-inrushing stability, as d/H<1.0. It gradually weakens with the increase of d/H, and nearly disappears when d/H exceeds critical ratio. The critical ratio of the diameter to the shaft depth increases linearly as the confined water head increases.

4) The soil strength contributes to resisting hydraulic uplift according to the analysis of failure mechanism, but the downward shear strength along the soil-wall interface should be partially considered based on the degree of the disturbance of the soil in the theoretical calculation.

References

[1] WANG Jian-feng, WANG Kang, ZHANG Tao, WANG Shuai. Key aspects of a DN4000 steel pipe jacking project in China: A case study of a water pipeline in the Shanghai Huangpu River [J]. Tunnelling and Underground Space Technology, 2017, 72: 323-332. DOI: 10.1016/j.tust. 2017.12.012.

[2] LIU Guo-bin, JIANG R J, NG C W W, HONG Yi. Deformation characteristics of a 38 m deep excavation in soft clay [J]. Canadian Geotechnical Journal, 2011, 48(12): 1817-1828. DOI: 10.1139/T11-075.

[3] NG C W W, HONG Yi, LIU Guo-bin, LIU Tao. Ground deformations and soil-structure interaction of a multi- propped excavation in Shanghai soft clays [J]. Géotechnique, 2012, 62(10): 907-921. DOI: 10.1680/geot.10.P.072.

[4] HONG Yi, NG C W W, LIU Guo-bin, LIU Tao. Three- dimensional deformation behaviour of a multi-propped excavation at a “greenfield” site at shanghai soft clay [J]. Tunnelling and Underground Space Technology, 2015, 45: 249-259. DOI: 10.1016/j.tust.2014.09.012.

[5] HONG Yi, NG C W W. Base stability of multi-propped excavations in soft clay subjected to hydraulic uplift [J]. Canadian Geotechnical Journal, 2013, 50(2): 153-164. DOI: 10.1139/cgj-2012-0170.

[6] WU Yong-xia, SHEN Shui-long, YUAN Da-jun. Characteristics of dewatering induced drawdown curve under blocking effect of retaining wall in aquifer [J]. Journal of Hydrology, 2016, 539: 554-566. DOI: 10.1016/j.jhydrol. 2016.05.065.

[7] CHEN Mu, SHEN Shui-long, WU Huai-na, WANG Zhi-feng, HORPIBULSUK S. Geotechnical characteristics of weathered granitic gneiss with geo-hazards investigation of pit excavation in Guangzhou, China [J]. Bulletin of Engineering Geology and the Environment, 2016, 76(2): 681-694. DOI: 10.1007/s10064-016-0915-1.

[8] TAN Yong, LU Ye. Forensic diagnosis of a leaking accident during excavation [J]. Journal of Performance of Constructed Facilities, 2017, 31(5): 04017061. DOI: 10.1061/(ASCE)CF. 1943-5509. 0001058.

[9] BSI. BS EN 1997: Eurocode 7: Geotechnical design – Part 1: General rules [R]. British Standards Institution (BSI), 2004.

[10] Ministry of Housing and Urban–Rural Development of the People’s Republic of China (MOHURD). Technical specification for retaining and protection of building foundation excavations. JGJ 120-2012 [R]. Chinese Academy of Architectural Sciences. 2012. (in Chinese)

[11] MILLIGAN V, LO K Y. Observations on some basal failures in sheeted excavations [J]. Canadian Geotechnical Journal, 1970, 7(2): 136-144. DOI: 10.1139/t70-017.

[12] WARD W H. The use of simple relief wells in reducing water pressure beneath a trench excavation [J]. Géotechnique, 1996, 119(4): 231-236. DOI: 10.1680/igeng.1996.28759.

[13] LIU Jin-long, LIU Jie-qun. Abrupt gush problem of foundation pit considering the influence of shear strength of soil [J]. Advanced Materials Research, 2010, 168-170: 1586-1589. DOI: 10.4028/www.scientific.net/AMR.168-170. 1586.

[14] YANG Jian-ming, ZHENG Gang. Classification of seepage failures and opinion to formula for check bursting instability in dewatering [J]. Rock and Soil Mechanics, 2009, 30(1): 261-264. (in Chinese)

[15] ZHANG Fei, LI Jing-pei, YANG Bo, TANG Yao. Centrifugal model tests on hydraulic heave mechanism of excavation in cohesive soil with confined water [J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 41(3): 2341-2347. (in Chinese)

[16] SUN Yu-yong. Experimental and theoretical investigation on the stability of deep excavations against confined aquifers in Shanghai, China [J]. KSCE Journal of Civil Engineering, 2016, 20(7): 2746-2754. DOI: 10.1007/s12205-016-0488-3.

[17] DING Chun-lin, LI Zhi-qing, WU Xu-ping, WU Ke-liang. Analysis on inducing factors to inrushing plastic deformation failure of foundation pit with confined water [C]// Geo-Shanghai 2014. Shanghai: ASCE, 2014: 491-501. DOI: 10.1061/9780784413449.048.

[18] HONG Yi, NG C W W, LIU Guo-bin. Initiation and failure mechanism of base instability of excavations in clay triggered by hydraulic uplift [J]. Canadian Geotechnical Journal, 2015, 52(5): 599-608. DOI: 10.1139/cgj-2013- 0343.

[19] WANG Jian-xun, LIU Xiao-tian, XIANG Ji-dong, JIANG Yun-hua, FENG Bo. Laboratory model tests on water inrush in foundation pit bottom [J]. Environmental Earth Sciences, 2016, 75(4): 1072. DOI: 10.1007/s12665-016-5861-5.

[20] YANG Yu-you, LU Jian-guo, HUANG Xue-gang, TU Xiao-ming. Sensor monitoring of a newly designed foundation pit supporting structure [J]. Journal of Central South University, 2013, 20(4): 1064-1070. DOI: 10.1007/ s11771-013-1585-9.

[21] GUAN Chen-li, YANG Yu-you, WANG Chen-biao. Rapid excavation with a newly developed retaining system: Spiral assembly steel structure [J]. Journal of Central South University, 2015, 22(7): 2719-2729. DOI: 10.1007/s11771- 015-2802-5.

[22] ZHAO Guo-qing, MENG Su-yun, GUAN Cheng-li, YANG Yu-you. Test study on stress and deformation behaviors of the shaft supported by a prefabricated prestressed structure [J]. Applied Sciences, 2019, 9(4): 629. DOI: 10.3390/ app9040629.

[23] BRINKGREVE R B J, KUMARSWAMY S, SWOLFS W M. Plaxis 2D 2015–User’s Manual. Plaxis BV [M]. Netherlands: Plaxis, 2015.

[24] SCHANZ T, VERMEER P A, BONNIER P G. The hardening soil model: Formulation and verification [C]// In: Beyond 2000 in Computational Geotechnics–10 Years Plaxis. Rotterdam: Plaxis, 1999: 281-296.

[25] BENZ T, VERMEER P A, SCHWAB R. A small-strain overlay model [J]. International Journal for Numerical & Analytical Methods in Geomechanics, 2009, 33(1): 25-44. DOI: 10.1002/nag.701.

[26] MU Lin-long, HUANG Mao-song. Small strain based method for predicting three-dimensional soil displacements induced by braced excavation [J]. Tunnelling and Underground Space Technology, 2016, 52: 12-22. DOI: 10.1016/j.tust.2015.11.001.

[27] LIAO Shao-ming, WEI Shi-feng, SHEN Shui-long. Structural responses of existing metro stations to adjacent deep excavations in suzhou, China [J]. Journal of Performance of Constructed Facilities, 2016, 30(4): 04015089. DOI: 10.1061/(ASCE)CF.1943–5509.0000845.

[28] ZHENG Gang, YANG Xin-yu, ZHOU Hai-zuo, DU Yi-ming, SUN Jia-yu, YU Xiao-xuan. A simplified prediction method for evaluating tunnel displacement induced by laterally adjacent excavations [J]. Computers and Geotechnics, 2018, 95: 119-128. DOI: 10.1016/j.compgeo.2017.10.006.

(Edited by HE Yun-bin)

中文导读

圆形竖井承压水破坏机理：试验和数值模拟研究

摘要：在中国广州市某高水压砂土地层拟进行顶管工作井施工。拟采用一种安全、高效、环保的新型装配式支护结构用于圆形工作井支护。本文通过现场原位试验和数值模拟，分析了圆形竖井受承压水作用下的基底破坏机理。现场试验获得了竖井基底在承压水作用下的破坏过程，并通过数值软件精细化模拟了竖井分层开挖和装配式结构逐层支护的施工过程。结果表明，模拟结果与施工现场现象吻合较好，基底破坏模式呈现出在基底中心的拉伸破坏和沿着土与支护结构接触面的剪切破坏。文章还讨论了竖井尺寸和承压水水头对基底失稳的影响规律，并提出了可用于评价圆形竖井尺寸效应的竖井直径与竖井深度的临界比值。通过对五种抗突涌安全系数计算方法的分析，得出在抗突涌安全系数计算时应部分考虑土体强度。本研究可为类似受承压水作用的圆形竖井基底稳定性评价提供参考。

关键词：圆形竖井；现场试验；有限元分析；基底稳定；突涌水

Foundation item: Project(2017YFC0805008) supported by the National Key Research and Development Program of China; Project(265201708) supported by the Fundamental Research Funds for the Central Universities, China

Received date: 2018-11-10; Accepted date: 2019-06-28

Corresponding author: YANG Yu-you, PhD, Professor; Tel: +86-10-82322294; E-mail: yangyuyou@cugb.edu.cn; ORCID: 0000-0002- 7385-2453