Application of reflux classifier with closely spaced inclined channels in pre-concentrate process of fine antimony oxide particles
来源期刊:中南大学学报(英文版)2020年第11期
论文作者:卢东方 褚浩然 刘振强 王毓华 郑霞裕 陈福林
文章页码:3290 - 3301
Key words:reflux classifier; antimony oxide; pre-concentration; inclined channels
Abstract: In this work, the reflux classifier with closely spaced inclined channels is used as the pre-concentration facility to improve the separation efficiency before the shaking table separation. Three operating parameters of reflux classifier (RC) to pre-concentrate fine(0.023-0.15 mm) tailings of antimony oxide were optimized by response surface methodology (RSM) using a three-level Box-Behnken design (BBD). The parameters studied for the optimization were feeding speed, underflow, and ascending water speed. Second-order response functions were produced for the Sb grade and recovery rate of the concentrate. Taking advantage of the quadratic programming, when the factors of feeding, underflow and ascending water are respectively 225, 30 and 133 cm3/min, a better result can be achieved for the concentrate grade of 2.31% and recovery rate of 83.17%. At the same time, 70.48% of the tailings with the grade of 0.20% were discarded out of the feeding. The results indicated that the reflux classifier has a good performance in dealing with fine tailings of antimony oxide. Moreover, second-order polynomial equations, ANOVA, and three-dimensional surface plots were developed to evaluate the effects of each parameter on Sb grade and recovery rate of the concentrate.

J. Cent. South Univ. (2020) 27: 3290-3301
DOI: https://doi.org/10.1007/s11771-020-4547-z

LIU Zhen-qiang(刘振强)1, LU Dong-fang(卢东方)1, WANG Yu-hua(王毓华)1,CHU Hao-ran(褚浩然)1, ZHENG Xia-yu(郑霞裕)1, CHEN Fu-lin(陈福林)2
1. School of Minerals Processing and Bioengineering, Central South University, Changsha 410083, China;
2. Pangang Group Research Institute Co., Ltd, Panzhihua 617000, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Abstract: In this work, the reflux classifier with closely spaced inclined channels is used as the pre-concentration facility to improve the separation efficiency before the shaking table separation. Three operating parameters of reflux classifier (RC) to pre-concentrate fine(0.023-0.15 mm) tailings of antimony oxide were optimized by response surface methodology (RSM) using a three-level Box-Behnken design (BBD). The parameters studied for the optimization were feeding speed, underflow, and ascending water speed. Second-order response functions were produced for the Sb grade and recovery rate of the concentrate. Taking advantage of the quadratic programming, when the factors of feeding, underflow and ascending water are respectively 225, 30 and 133 cm3/min, a better result can be achieved for the concentrate grade of 2.31% and recovery rate of 83.17%. At the same time, 70.48% of the tailings with the grade of 0.20% were discarded out of the feeding. The results indicated that the reflux classifier has a good performance in dealing with fine tailings of antimony oxide. Moreover, second-order polynomial equations, ANOVA, and three-dimensional surface plots were developed to evaluate the effects of each parameter on Sb grade and recovery rate of the concentrate.
Key words: reflux classifier; antimony oxide; pre-concentration; inclined channels
Cite this article as LIU Zhen-qiang, LU Dong-fang, WANG Yu-hua, CHU Hao-ran, ZHENG Xia-yu, CHEN Fu-lin. Application of reflux classifier with closely spaced inclined channels in pre-concentrate process of fine antimony oxide particles [J]. Journal of Central South University, 2020, 27(11): 3290-3301. DOI: https://doi.org/10.1007/s11771-020- 4547-z.
1 Introduction
Antimony is a rare metal element, which is of low content in the crust. It is usually found as sulfide minerals. Industrially, stibnite(Sb2S3) is the predominant ore of interest and importance [1]. With the exploitation of stibnite, antimony resources become more and more scarce, and the proportion of antimony oxide resources is increasing. For example, the antimony oxide rate of Xikuangshan Miner, located northeast of Lengshuijiang city, Hunan province, China, is as high as 50%. Due to the complex composition and extremely poor floatability of antimony oxides, there is a huge amount of antimony loss in flotation tailings [2-4]. Shaking table is the main technique for the separation of antimony oxidized ore tailings, but the recovery rate of antimony is only about 20%, and the treatment capacity and operating stability were low [5].
In coal and mineral processing, gravity separation of fine particles less than 2 mm in size is normally achieved in water through the application of an autogenously dense medium. The reflux classifier was invented by KP Galvin in 2002 and it’s a relatively new gravity separation device that combines a system of parallel inclined channels above a conventional fluidized bed [6-9]. The inclined channels provide a significant hydraulic advantage over conventional fluidized beds, consistent with the well-known “Boycott Effect” [10-13]. The analysis of the previous work was limited primarily to the separation of coal and mineral matter, with the particle size range of 0.25– 2.0 mm. And with the decrease of the particle size of the material, it will be more difficult to separate the particles according to the density.
With the very narrow channels used in the present study, much higher local velocities are produced near the plate surface because of the higher shear rate. For particles that settle in the intermediate regime [14], the terminal velocity varies almost linearly with the particle diameter. Here, 1
In developing an alternative model, GALVIN et al [8] found that a conventional force balance on a particle in the tangent direction of the inclined channel provided an excellent description of the results. The weight force of the particle in the tangent direction was balanced by the hydrodynamic drag force arising from the local fluid flow. The contact force of friction was neglected because of the significant lift force. Thus,
 (1)
(1)
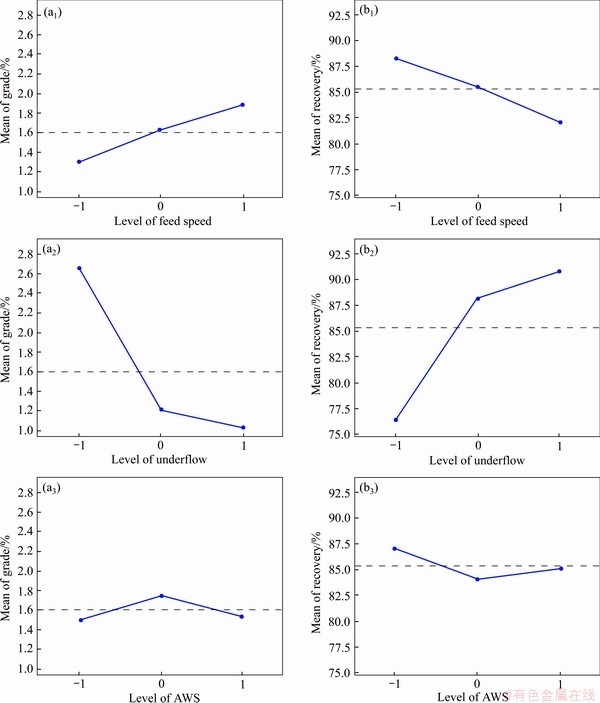
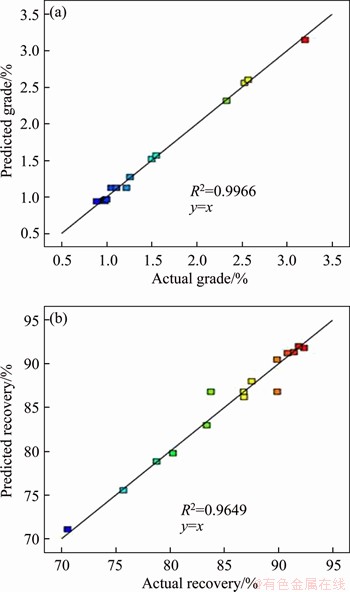
where u is the local fluid velocity, and CDW the drag coefficient at the wall obtained by correcting the standard drag coefficient, CD, using CDW=βCD. The wall correction factor, valid for d< For a particle resident at the inclined surface, the local fluid velocity is defined by the value one in particle radius from the inclined surface. Noting the exact velocity profile for laminar flow through a channel [16], and then taking the linear approximation, the local fluid velocity in one particle radius from the inclined surface is where U′ is the average hydraulic velocity; d is the particle diameter; z is the perpendicular channel spacing. Assuming that the terminal velocity in the tangent direction, U′t, matches the magnitude of the local fluid velocity, u, one particle radius from the inclined surface, the hydraulic velocity is given by Equation (4) describes the relationship between the hydraulic velocity, U′, of a fluid through an inclined channel of gap, z, and the terminal velocity, U′t, of a particle of diameter, d, that exhibits an equal tendency to either slide downwards or convey upwards. As can be seen from Figure 1, the curve will become steeper as z decreases, which will result in flat parts of the curve of different densities becoming fewer. At a certain channel velocity, small-size high-density particles passing through the inclined channel will be reduced to achieve better density separation. Following the work of LASKOVSKI et al [17] it was concluded that improved separation performance would be achieved using narrower channels. And GALVIN et al [18] found that by using closely spaced inclined channels it is possible to achieve significant suppression of the effects of particle size, and hence produce a powerful separation based on density. SYED et al [19] developed a 2D continuous segregation-dispersion model incorporating a laminar-shear separation mechanism to describe the reflux classifier. It shows that the narrow inclined channels promote the laminar-shear mechanism, leading to the selective shear-induced lift of low-density particles while allowing the fine and denser particles to deposit onto the inclined surfaces, and slide downwards. This mechanism allows a sharp density-based separation. Figure 1 Dependence of PVC separation size on hydraulic velocity through inclined channels Therefore, the reflux classifier with closely spaced inclined channels can be used as the pre-concentration facility to improve the separation efficiency before the shaking table separation. However, it is needed for a scientific investigation under different operating variables to adopt the RC in preliminary enrichment of fine tailings of antimony oxidize. And the response surface technique was one of the most popular methodologies in modelling and optimizing. Response surface methodology (RSM) was firstly proposed by BOX and WILSON [20] and is mainly applied in the field of the chemical industry. The preliminary enrichment process can be optimized by developing a second-order mathematical model that can be got from RSM. By analyzing the function model, the direct and interactive effects of process parameter through three-dimensional plots will be easy to get. Furthermore, finding a set of an optional process parameters, which can get a better sorting effect, can be achieved as well. A typical second-order model utilized in RSM can be expressed by Eq. (5): where y is the response influenced by variables (xj); αj and αij are unknown coefficients; ε is a random error. By using the least square method, all of these unknown coefficients in the model can be determined [21]. 2 Materials and methods 2.1 Samples The flotation tailings of an antimony concentrator in Hunan province in China were used for the present investigation. The feed sample was prepared in the size fraction of 0.023-0.15 mm and subjected to the XRD (X-ray diffraction) for the identification of the mineral phase which is shown in Figure 2. The particle size analysis results detected by the laser particle sizer are shown in Figure 3. The results of the multi-element analysis are shown in Table 1. It is observed in Figure 2(a) that, the main gangue minerals are quartz along with little mica, calcite, and kaolinite. Minerals containing antimony were not detected because of low content. In order to determine the type of antimony minerals, the ore was concentrated by shaking table before being subjected by XRD, and it is apparent in Figure 2(b) that antimony-bearing minerals are mainly stibiconite. From Figure 3, the average size of the sample is 75.01 μm, and the d50 is 70.13 μm. The results of multi-element analysis (Table 1) showed that the Sb grade is 0.80%, the Si content is 42.425%, and the O content is 51.465%, both accounting for nearly 94% of the total content. Besides Sb, the content of other metals is too low to be worth recycling. Figure 2 XRD patterns of ore of 0.023-0.15 mm before (a) and after (b) concentrated by shaking table Figure 3 Size analysis results: Table 1 Ore multi-element analysis in mass fraction 2.2 Reflux classifier As shown in Figure 4, a laboratory-scale reflux classifier was manufactured in this investigation. The cylinder structure is mainly composed of two parts, the vertical column, and the inclined plates area. Two ascending water inlets were set symmetrical on the bottom of the device. Feeding inlet of the ore pulp is located in the middle and upper part of the vertical column. The cross-section of the column is a square with a side length of 50 mm, and the top of the vertical column is the inclined plates area, in which the organic glass plates with a smooth surface are placed in parallel equidistance. The thicknesses of the inclined plate, as well as the width of every channel, are both 2 mm. The angle between the incline and the horizontal plane is 70°. In the experiment, the prepared slurry with a mass concentration of 30% is added to the mixing bucket. After stirring, the pulp begins to enter the column through the feeding inlet. Meanwhile, the underflow peristaltic pump and the rising water start to set the flow. Then collect the slurry from underflow and overflow at different time points. After filtration, drying and sample preparation, the equilibrium point of both mass and metal quantity is selected as the final experimental result. Two preparatory works carried out before this study are as follows: 1) A set of experimental systems was arranged firstly. The flowsheet used for the RC text is presented in Figure 5. 2) We had carried out conditional experiments on the operating parameters of the RC [22], and concluded that feeding speed, underflow rate and ascending water rate have a great impact on the efficiency of separation, and determined a reasonable range of experimental conditions, which is feeding speed range from 225 to 325 cm3/min, underflow of 30-60 cm3/min and ascending water of 133-267 cm3/min. 2.3 Methods In this study, three mean variables as feeding speed (cm3/min), underflow (cm3/min) and ascending water speed (cm3/min) were arranged at the three levels (±1, 0), and Sb grade and recovery rate of the concentrate were chosen as responses. If the replicate number of the central points is three, a three-variable, three-level 15-run (32+3+3=15) Box–Behnken design (BBD) is required [23, 24]. The variables and their levels are shown in Table 2. The arrangement of the reflux classifier experiments is shown in Table 3. Figure 4 Schematic of reflux classifier Figure 5 Flow sheet for reflux classifier text: 1-Mixing bucket; 2-Valve; 3-Peristaltic pump for feeding; 4-Reflux classifier; 5-Peristaltic pump for underflow The function model based on Eq. (6) can be expanded as the following form: where y is the predicted response; α0 is the model constant; x1, x2 and x3 are the variables; α1, α2 and α3 are linear coefficients; α12, α13 and α23 are cross-product coefficients, α11, α22 and α33 are the quadratic coefficients. After getting the experimental results of the BBD, all of the coefficients can be estimated by computer simulation programming applying the least square method using the mathematical software package (Design Expert 10.0). Table 2 Variables with respective ranges used in BBD Table 3 Coded and actual variables of RC experiments In addition, analyses of variance of the main effects were carried out by analyzing the confidence intervals of the effects with a significance level of 0.05. As such, any factor with a p-value lower than 0.05 was considered to influence the response variable with statistical significance. Use a main effect plot to examine differences between level means for one or more factors. There is a main effect when different levels of a factor affect the response differently. And the main effect plot was created by Minitab 3 Results and discussion From the experimental results of the reflux classifier experiments, the second-order response functions representing the Sb grade of the concentrate and recovery rate of antimony could be expressed as functions of the feeding speed (x1), underflow (x2) and ascending water (x3). The model equations for two responses (grade, y1, and recovery rate, y2) are presented in Eqs. (7) and (8) respectively. Analysis of variance (ANOVA) is given in Tables 4 and 5, for the sake of estimating the significance of the models. It is shown that the calculated F-values of two models (y1 and y2) are 162.72 and 15.29, respectively. By comparing the values with the standard from the F-statistics table with p=0.01 (F0.01(9,5)=10.16), a confidence level higher than 99.99% was achieved, which means that the regression is acceptable. The model p-values (0.000 for y1, 0.004 for y2) are both less than 0.05, and it indicated that model terms are significant. Moreover, the lake-of-fit items of the two models are both higher than 0.05, which implies that it is not significant relative to the pure error and demonstrates that these two models of quadratic are valid for this investigation. The relationship between actual and predicted values of grade and recovery rate is shown in Figure 6. From both the plots, it can be observed that most of the data points are well distributed near to the straight line, suggesting a good relationship between the actual predicted values of the responses. It was found that the coefficient of determination (R2) is very high for the grade (0.9966) which indicates that more than 99% of the variation for Sb grade of the concentrate can be explained by the three variables. Similarly, it can be concluded that y2 with a high R2 value of 0.9649 implies a good correlation between the actual and predicted values. The residual plots for the predicted values of grade and recovery rate are plotted in Figure 7. From the figures, it can be observed that, the residual values are scattered randomly, which means that the errors for both grade and recovery rate are well distributed, suggesting that the predictions of the models are adequate. Table 4 ANOVA table for y1 Table 5 ANOVA table for y2 Figure 6 Relationship between actual and predicted grade (a) and recovery rate (b) 3.1 Effects of process variables on Sb grade of concentrate From Table 4, the p-values of x1 (feeding speed) and x2 (underflow) are both 0.000, which means that the response (y1) is significantly affected by these two factors. Moreover, according to Eq. (7), the linear term of x1 showed a positive signal. It indicate that an increase of factor values tends to increase the response values. On the other hand, negative values of coefficient of x2 indicate that an an increase tends to decrease the responses. The cross effect between x1 and x2 is also significant to y1, with a p-value of 0.018 (less than 0.05), and a negative value of the coefficient signifies a negative effect on the response when it increases. Figure 7 Residual plots for predicted grade (a) and recovery rate (b) Table 6 Actual and predicted values of grade and recovery rate In addition, the quadratic term of feeding speed Three-dimensional graphs of the response surface (Figure 8) were constructed according to Eq. (7). These illustrated the correlations among three independent variables and the response (grade of concentrate, %). Each three-dimensional response surface graph is a function of two factors, keeping the third at its central point. From Figure 8(a), it is clear that as the feeding speed increases from 225 to 325 cm3/min, the increasing rate of grade is high, i.e., 0.78% to 3.15%. The grade decreases because of the increase in the underflow. 3D response surface plot shows the weaker effect of ascending water speed comparing to the other two factors. 3.2 Effects of process variables on Sb recovery rate of concentrate Linear effects, which have a significant influence on the response of Sb recovery rate, are x1 (feeding speed) and x2 (underflow), with a p-value of 0.008 and 0.000, respectively. Feeding speed contributes a negative effect on Sb recovery rate, with a coefficient of -3.13, while increasing the underflow is beneficial for achieving a high Sb recovery rate (coefficient of x2 is 7.23). From Table 5, it is clear that none of the cross-effects is significant to the response (y2), because the p-values are 0.285, 0.572 and 0.550 (higher than 0.05), respectively, for x1x2, x1x3, and x2x3. Additionally, with a p-value of 0.017, the quadratic term of underflow Further, when Eq. (8) has been determined, the response surface plots (Figure 9) for Sb recovery rate can be easy to get. The figures show the relationship between two variables and responses while the other variable is at the central level. It is noted in Figure 9(a) that Sb recovery rate ranges from 70.55% to 92.34% when the feeding speed and underflow vary, which implies that the response is significantly influenced by these two factors. From Figures 9(b) and (c), it can be seen that ascending water speed proved a minor effect on Sb recovery rate. Figure 8 Response surface plots for Sb grade of concentrate Figure 9 Response surface plots for Sb recovery rate 3.3 Main effects Main effects plot is used to see how one or more categorical factors influence the continuous response, and we can more intuitively observe the significance of the factors from the main effects plot. This is illustrated in Figure 10. The main effects plot of grade and recovery rate displayed data means that were the raw response variable means for each factor level combination. From the main effects plot of grade and recovery rate (Figure 10), the main effect curve of FS and underflow are not horizontal, and then there is the main effect. And the curve of AWS is relatively gentle, indicating that the main effect of AWS is low, so we wouldn’t discuss the main effects of it. It can be seen from the main effects plot of grade (Figure 10(a)) that, compared with the other two process variables, the shape of the curve of underflow is steeper, which indicates that for the grade of concentrate, the influence of the change of underflow rate is significant, and the decrease of underflow rate will greatly improve the grade of concentrate. Similarly, the main effects plot of recovery rate (Figure 10(b)) shows that the underflow was also the significant effect for recovery rate, but it is different from the plot of grade, that the decrease of underflow would result in a drastic reduction in the recovery rate. This also corresponds to the above mentioned analysis. 3.4 Process optimization One of the main objectives of this study is to optimize the separation process and obtain a maximum concentrate grade and Sb recovery rate by analyzing the function determined in this investigation, and this process can be achieved by using the mathematical software package (Design Expert 10.0). To acquire the maximum Sb grade (a) or recovery rate (b) or a comprehensive consideration of both grade and recovery rate factors (c), the process variables after being optimized are showed in Table 7. Further, the result of this simulation is verified by experiment. The actual experimental result shows that using the optimized process variables, Sb grade of 2.31% was achieved with Sb recovery rate of 83.17%. At the same time, 70.48% of the tailings with the grade of 0.20% were discarded out of the feeding. In the experiment of pre-concentrate about the same fine antimony oxide tailings with reflux classifier, ZENG [22] found that when the feeding rate was 300 mL/min, the underflow was 30 mL/min and the ascending water speed was 8 L/h, the concentrate of Sb grade of 2.54%, recovery rate of 73.91% and separation efficiency of 49.0% can be obtained. And the separation efficiency was in order to consider the grade and recovery rate index comprehensively, and it was calculated by Eq. (9). According to Eq. (9), the separation efficiency of result using the optimized process variables is 54.22% and it has 5.22% more than the previous results. This indicates that through the optimization in this investigation, the reflux classifier has a better separation effect to pre-concentrate the antimony oxidized ore tailings. Figure 10 Main effects plot of grade (a) and recovery rate (b) Table 7 Optimized process variables 4 Conclusions In this study, the reflux classifier with closely spaced inclined channels is used as the pre-concentration facility to improve the separation efficiency before the shaking table separation. A three-level Box–Behnken factorial design combining with a response surface methodology and the main effects plot were used to analyze and optimize three operating parameters of a laboratory- scale reflux classifier in preconcentration of antimony oxide tailings in the size range of 0.023-0.15 mm. The results are as follows: 1) For the Sb grade and recovery rate of concentrate, the factors influencing the response significantly are linear effects of feeding speed (x1), underflow (x2) and cross effect of x1x2. In these variables, linear effects of x1 showed positive effects on the response of grade, while linesr effects of underflow (x2) and cross effect of x1x2 provide a negative contribution. In contrast, for the Sb recovery rate, increasing the linear effect of underflow (x2) is a benefit for the response to get a higher level, and linear effects of feeding speed (x1) provide a negative contribution in Sb recovery rate. 2) Moreover, using quadratic programming, a set of the optimized operating parameters were obtained for a better separating process. A verification test shows that Sb concentrate with a grade of 2.31% and recovery rate of 83.17% can be achieved when feeding speed, underflow and ascending water are respectively 225, 30, and 133 cm3/min. At the same time, 70.48% of the tailings with a grade of 0.20% were discarded out of the feeding. It is apparent that the reflux classifier has its advantage in dealing with fine tailings of antimony oxide. In this paper, the potential of the reflux classifier to pre-concentrate fine tailings of antimony oxide was demonstrated, especially for the size of 0.023-0.15 mm. However, the performance of RC to deal with particles coarser than 0.15 mm and finer than 0.023 mm needs to be specifically assessed. For coarser particles, the liberation problems should be considered firstly. And then, more investigation on structure parameters of RC, especially the width of the inclined channels is needed in this part. Dealing with particles finer than 0.023 mm is still a great challenge in mineral processing. The tendency to concentrate these particles is using a selective flocculation method to increase the particle diameter and reduce the viscosity of the pulp system. All of these need a series of further researches. Contributors LIU Zhen-qiang wrote the first draft of the manuscript and revised the manuscript. LU Dong-fang provided the research ideas and formulated the overall research objectives. CHU Hao-ran conducted the experiments and analyzed the test data. WANG Yu-hua, ZHENG Xia-yu and CHEN Fu-lin offered some valuable suggestions for the contents of the manuscript. Conflict of interest LIU Zhen-qiang, LU Dong-fang, WANG Yu-hua, CHU Hao-ran, ZHENG Xia-yu and CHEN Fu-lin declare that they have no conflict of interest. References [1] ANDERSON C G. The metallurgy of antimony [J]. Chemie der Erde, 2012, 72: 3-8. DOI: 10.1016/j.chemer.2012. 04.001. [2] GUTKNECHT T, FORSGREN C, STEENARIA B M. Investigations into high temperature separation of antimony from metal oxide varistors [J]. Journal of Cleaner Production, 2017, 162: 474-483. DOI: 10.1016/j.jclepro.2017.06.033. [3] GUO Zhen-xun. Antimony ore processing technology [J]. Foreign Metal Ore Processing, 1983(6): 13-23. (in Chinese) [4] LAI Ren-kui, YU Jian-yi, LIU Bang-rui. New method of flotation separation of antimony oxide and quartz [J]. China Mine Engineering, 1991(2): 44-45. (in Chinese) [5] WANG Jin-ming, WANG Yu-hua, YU Shi-lei, YU Sheng-li, YU Fu-shun. Flotation behavior and mechanism of cervantite with sodium dodecyl sulfate [J]. Journal of Central South University (Science and Technology), 2013, 44(10): 3955- 3962. (in Chinese) [6] GALVIN K P, DOROODCHI E, CALLEN A M, LAMBERT N. PRATTEN S J. Pilot plant trial of the reflux classifier [J]. Minerals Engineering, 2002, 15: 19-25. DOI: 10.1016/ S0892-6875(01)00193-5. [7] GALVIN K P, CALLEN A, ZHOU J, DOROODCHI E. Gravity separation using a full scale reflux classifier [M]// MEMBREY W B. Proceedings, Tenth Australian Coal Preparation Conference, Paper 2004.H21. [8] GALVIN K P, CALLEN A, ZHOU J, DOROODCHI E. Performance of the reflux classifier for gravity separation at full scale [J]. Minerals Engineering, 2005, 18: 19-24. DOI: 10.1016/j.mineng.2004.05.023. [9] GALVIN K P, WALTON K, ZHOU J. How to elutriate particles, according to their density [J]. Chemical Engineering Science, 2009, 64: 2003-2010. DOI: 10.1016/ j.ces.2009.01.031. [10] BOYCOTT A E. Sedimentation of blood corpuscles [J]. Nature, 1920, 104: 532. DOI: 10.1038/104532b0. [11] PONDER P. On sedimentation and Rouleaux formation [J]. Quarterly Journal of Experimental Physiology, 1925, 15: 235-252. DIO: 10.1113/expphysiol.1925.sp000356. [12] NAKAMURA H, KURODA K. The cause of the accelerated sedimentation rate of suspensions in inclined channel [J]. Keijo Journal of Medicine, 1937, 8: 256-296. http://c.21-bal. com/law/7087/index.html. (in French) [13] ZHOU J, WALTON K, LASKOVSKI D, DUNCAN P, GALVIN K P. Enhanced separation of mineral sands using the reflux classifier [J]. Minerals Engineering, 2006, 19: 1573-1579. DOI: 10.1016/j.mineng.2006.08.009. [14] VANCE W H, MOULTON R W. A study of slip ratios for the flow of steam–water mixtures at high void fraction [J]. AIChE Journal, 1965, 11(6): 1114-1124. DIO: 10.1002/ aic.690110628. [15] MUNROE H S. The English versus the continental system of jigging-is close sizing advantageous [M]. Transactions of the American Institute of Mining Engineers, 1888,17: 637-659. [16] BIRD B, STEWART W, LIGHTFOOT. Transport phenomena [M]. New York: John Wiley and Sons, 1976: 62. DOI: 10.1002/aic.690070245. [17] LASKOVSKI D, DUNCAN P, STEVENSON P, ZHOU J, GALVIN K P. Segregation of hydraulically suspended particles in inclined channels [J]. Chemical Engineering Science, 2006, 61: 7269-7278. DOI: 10.1016/j.ces.2006. 08.024. [18] GALVIN K P, ZHOU J, WALTON K. Application of closely spaced inclined channels in gravity separation of fine particles [J]. Minerals Engineering, 2010, 23: 326-338. DOI: 10.1016/j.mineng.2009.09.015. [19] SYED N H, DICKINSON J E, GALVIN K P, MORENO-ATANASIO R. Continuous, dynamic and steady state simulation of the reflux classifier using a segregation- dispersion model [J]. Minerals Engineering, 2018, 115: 53-67. DOI: 10.1016/j.mineng.2017.10.010. [20] BOX G E P, WILSON K B. On the experimental attainment of optimum conditions (with discussion) [J]. Journal Royal Statistical Society, 1951, 8: 622-654. DOI: 10.1111/ j.2517-6161.1951.tb00067.x. [21] MYERS R H, MONTGOMERY D C. Response surface methodology [M]. New York: Wiley and Sons, 1995. [22] ZENG Fan-sen. Experimental study and flow field simulation of pre-concentrate of cervantite by Reflux Classifer [D]. Changsha: Central South University, 2017. (in Chinese) [23] TRIPATHY S K, MURTHY Y R. Modeling and optimization of spiral concentrator for separation of ultrafine chromite [J]. Powder Technology, 2012, 221: 387-394. DOI: 10.1016/ j.powtec.2012.01.035. [24] ASLAN N. Modeling and optimization of multi-gravity separator to produce celestite concentrate [J]. Powder Technology, 2007, 174: 127-133. DOI: 10.1016/j.powtec. 2007.01.007. (Edited by YANG Hua) 中文导读 逆流分选柱预富集细粒级氧化锑尾矿的建模与优化 摘要:本文采用窄斜板间距的逆流分选柱作为摇床分选前的预富集装置,旨在提高其分选效率。采用响应面法(RSM),并利用三层Box-Behnken design (BBD)对逆流分选柱(RC)预富集细粒级氧化锑尾矿(0.023~0.015 mm)的三个操作实验参数进行优化。优化研究的参数为给矿速度、底流速度、上升水流速。用二阶响应函数对精矿产物的锑品位和精矿回收率进行拟合,并利用二次规划法对实验操作参数进行优化,可得当给矿速度、底流速度、上升水流速分别为225、30和133 cm3/min时,可得品位为2.31%,回收率为83.17%的精矿产品。同时,有70.48%的品位为0.20%的尾矿被抛除。结果表明,该逆流分选柱对氧化锑细粒尾矿的处理效果较好。此外,还建立了二阶多项式方程、方差分析和三维曲面图来评价各操作参数对锑品位和精矿回收率的影响。 关键词:逆流分选柱;氧化锑矿;预富集;沉降斜板 Foundation item: Project(2015SK20792) supported by Key Province Key Technology Research and Development Program of the Ministry of Science and Technology of Hunan, China; Projects(2019zzts703, 2020zzts740, 2020zzts202) supported by the Fundamental Research Funds for the Central Universities of China; Project(2020P4FZG03A) supported by State Key Laboratory of Vanadium and Titanium Resources Comprehensive Utilization, China Received date: 2020-01-22; Accepted date: 2020-07-15 Corresponding author: LU Dong-fang, PhD, Professor; Tel: +86-731-88830115; E-mail: ludongfang7700108@163.com; ORCID: https://orcid.org/0000-0003-2501-5260; CHU Hao-ran, PhD; Tel: +86-18774931631; E-mail: 924921382@qq. com; ORCID: https://orcid.org/0000-0001-8381-4058 (2)
(2) (3)
(3) (4)
(4)
 (5)
(5)





 (6)
(6)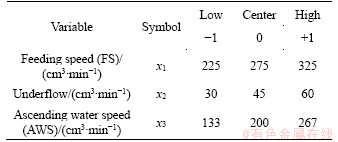

 18 software.
18 software.

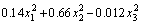 (7)
(7)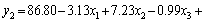
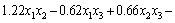
 (8)
(8)



 with a positive coefficient value of 1.40 and p-value of 0.015, has a positive quadratic effect on grade of concentrate, and the quadratic term of underflow
with a positive coefficient value of 1.40 and p-value of 0.015, has a positive quadratic effect on grade of concentrate, and the quadratic term of underflow with p-value of 0.000 and a positive coefficient in Eq. (7) indicates a positive quadratic effect on grade as well.
with p-value of 0.000 and a positive coefficient in Eq. (7) indicates a positive quadratic effect on grade as well. preformed a negative effect on the Sb recovery rate as a negative coefficient in Eq. (8)
preformed a negative effect on the Sb recovery rate as a negative coefficient in Eq. (8)

 (9)
(9)