深V型无人艇附加质量计算及其影响
孙寒冰，邹劲，庄佳园，吴恭兴
(哈尔滨工程大学 水下智能机器人技术重点实验室, 黑龙江 哈尔滨，150001)
摘要：针对某深V艇型无人艇惯性类水动力的计算方法进行研究，采用Hess-Smith方法计算三维物体在流体中运动的附加质量并经椭球算例验证。在实际计算中根据该艇模型试验测得的升沉及纵倾角得到其入水体积及形状，充分考虑滑行艇航速对附加质量的影响。建立无人艇6自由度运动方程，分别使用经验公式和Hess-Smith方法得到的2组附加质量值对无人艇运动状态进行仿真计算，并将结果与实艇海试结果进行对比。对比结果表明：附加质量对无人艇的运动状态有一定影响，在计算滑行艇附加质量时，考虑航速影响的仿真结果更加接近真实情况。
关键词：无人艇；深V型滑行艇；附加质量；Hess-Smith方法
中图分类号：U661.3 文献标志码：A 文章编号：1672-7207(2011)S1-0567-07
Calculation of added mass to deep-V unmanned surface vehicle and its effect
SUN Han-bing, ZOU Jin, ZHUANG Jia-yuan, WU Gong-xing
(State Key Laboratory of Autonomous Under Water Vehicle, Harbin Engineering University, Harbin 150001, China)
Abstract: A computation method for calculating added mass of an unmanned surface vehicle (USV) maneuvering in water was developed using Hess-Smith method, which was verified by the ellipsoid. Based on the results of model tests, the trim angle and the draft were obtained to calculate water entry shape of the USV, so that the influence of speed to added mass was considered. Then the six-degree-of-freedom dynamic equations were established according to theory mechanics, and different parameters of USV motion were achieved with the results of the empirical formula and Hess-Smith method respectively. Finally, the results were compared with the sea-experiments results of USV. The results show that the added mass has a considerable effect on USV motion and the simulation result considering speed effect is more approach to the actual situation, the feasibility of the method is verified.
Key words: unmanned surface vehicle; deep-V planing-hull; added mass; Hess-Smith method
近年来，一种新型智能水面无人艇受到世界各主要强国的高度重视，得到了快速发展[1]。目前已有多种无人艇应用于军事、科研等领域[2]。无人艇是指以遥控或自主模式在水面航行的航行器，能够执行危 险、枯燥以及其他不适于有人船只执行的军事任务，是水中情报收集、监视、侦察等军事用途不可多得的水面载体[3-4]。目前无人艇的典型代表主要有：美国的“SPARTAN”号、以色列的“Protector”号、意大利的“Charlie”号双体型USV[5]和英国的“Springer”号双体型USV[6]、葡萄牙的“Delfim”号双体型USV等。
由于无人艇要求高航速，因此，本研究中的无人艇采用深V滑行艇型作为其作战平台。滑行艇在高速小艇领域中有着重要地位，主要依靠航行时艇体产生的流体动升力支托大部分艇体质量[7]。而由于无人艇任务特性，要求其必须具有自主航行和安全航行的能 力，研究其受力情况和运动情况就显得尤为重要。目前，国内关于滑行艇受力分析的研究存在着很大空间。考虑到无人艇具有航速高、排水量小及水动力特性复杂等特点，而对其水动力进行分析计算能够为无人艇的运动控制提供基础，因此，对滑行艇的研究有着重要的研究意义及实用价值。
本文作者重点研究该无人艇惯性类水动力。当物体加速运动时，会带动周围流体一起运动，此时产生的流体惯性力可用附加质量来表示[8]。众所周知，根据流体力学原理，体积越大的物体所受到的流体惯性力越大，而且在坐标系选定后，在一般情况下，附加质量仅与物体的几何外形有关。利用理论流体力学知识可以计算简单几何体如圆球、椭球等的附加质量，而在实际工程中遇到的物体，形状大都不是简单几何 体，目前主要采用以下3种方法来求解三维物体的附加质量：纯估算法、切片法和边界元法(势流理论法)[9]。纯估算法是指用理论流体力学导出的椭球体等简单几何体的附加质量，从而近似估算细长体的附加质量。虽然在计算细长体时效果很好，但该方法具有一定的局限性；切片法是指沿物体轴线方向将其分成多段，每一小段的附加质量按相同几何形状的二元物体的附加质量公式计算，然后，把算得的各段附加质量叠加起来，得到该物体的附加质量；边界元法(BEM)是将物体表面划分单元，在每一个单元上布置强度待定的基本解，如源、汇、偶极子等，从而确定流场速度势，进而得到附加质量[10]，具有较高的精度。另外，随着计算机的高速发展，采用CFD等数值方法计算船舶 附加质量得到了广泛的应用[11-12]。
本研究的研究对象具有滑行艇水动力特性，随着航速变化，其航行状态和入水的船体形状也要随之变化，故其附加质量不单单是形状体积等物理参数的函数，还是一个与航速有关的函数。单纯依靠理论方法或经验公式进行计算已经不能满足准确性要求。可 见，对无人艇附加质量进行深入研究是十分必要的，本研究采用Hess-Smith方法来计算无人艇附加质量，并与实船海试结果对比，验证方法的可行性。
1 动力学模型建立及分析
1.1 坐标系及运动方程的建立
为了把复杂的物理世界用数学公式描述，本研究进行如下基本假设：
(1) 假设海面是惯性参考系，即假设地面坐标系为惯性坐标系；
(2) 忽略地球曲率，把海面看成平面；
(3) 重力加速度、大气密度以及海水密度恒定；
(4) 该无人艇艇体是刚体，且质量为常数；
(5) 该无人艇艇体是以纵剖面对称的。
为了描述无人艇的运动状态，采用下述2个右手直角坐标系：1个是固定坐标系O-XEYEZE(以下简称“定系”)固联于地球表面，O是任意选定的固定于地球表面的一点，通常可选择在某一时刻(t=0时)无人艇重心G所在位置，OXE轴在静水面内，其方向一般选在无人艇总的运动方向上；考虑风浪流时指向正北方 向，OYE轴选择为OXE轴在静水面内顺时针旋转90°的方向上，OZE轴垂直于静水面，以指向地心为正；另外1个是运动坐标系G-xyz(简称“动系”)固联于无人艇，随其一起运动。动系的原点在重心G，其坐标轴Gx，Gy和Gz分别是经过G的与水线面、横剖面和纵中剖面的交线。正反向按右手系的规定，即Gx向首，Gy向右，Gz向下，见图1。
图1 无人艇的定系及动系
Fig.1 Earth-fixed and body-fixed coordinate system of USV
坐标系建立之后，根据欧拉方程及质心运动定 理，相对于质心运动的动量矩定理可以推导出滑行艇6自由度操纵运动模型，即
(1)
式中：u，v和w分别为无人艇重心处的速度V在G- xyz坐标x，y和z方向上的投影；p，q和r分别为角速度W在x，y和z方向上的投影；X，Y和Z分别为力F在x，y和z方向上的投影；L，M和N分别为力矩H在x，y和z方向上的投影；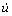
，
，
，
，
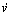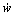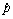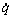和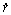
是各相应参数的加速度。
1.2 无人艇受力分析
滑行艇与一般排水式船舶相比具有很大的不同，其运动状态根据体积傅汝德数可分为[13]：
(1) 排水航行状态(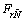
＜1.0)。在此阶段，艇重大部分由浮力支持，其艇体受力基本上与普通的排水型船只相同。
(2) 过渡航行状态(1.0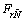＜＜3.0)。艇重由流体静浮力和动升力支持，随着航速升高，动升力增加，静浮力减少。
(3) 滑行状态(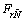＞3.0)。艇重几乎完全由流体动升力支持。
由于滑行艇具有这3个受力完全不同的航行状态，本研究根据受力分类法来分析滑行艇在航行过程中受到的各种力和力矩，将滑行艇的受力分为重力、浮力、水动力及外力，以此来分析滑行艇受到的各种力(矩)，既兼顾了低速时占大部分的静水力，又考虑了高速时动升力对滑行艇的影响。
下面重点分析该无人艇的惯性类水动力，惯性类水动力是指船在无限深广的平静水面上做操纵运动时由惯性引起的水动力。由流体力学原理可知，物体在无边际理想流体中流动时，流体扰动运动的动能为：
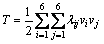
(2)
其中：v1=u；v2=v；v3=w；v4=p；v5=q；v6=r。而λij可组成一个6×6的矩阵，这里的附加质量是广义的，具有不同的因次。当i, j=1, 2, 3时，λij的量纲是质量；在i, j=4, 5, 6时，λij具有质量惯性矩的量纲。
将式(2)展开得到：
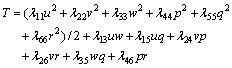(3)
而流体扰动运动的动量与动能有以下关系：
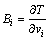
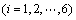(4)
随船运动坐标系和固定坐标系之间动量和动量矩的转换关系如下：
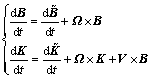(5)
船舶所受惯性类水动力FI和力矩MI为：
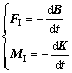(6)
将式(3)代入式(4)中，可得动量表达式，将其及式(5)一起代入式(6)即可得到6自由度运动时，作用于船体的惯性类水动力，在此基础上写成有关的投影式并根据滑行艇艇型的特殊性(艇底形状比较扁平)及附加质量矩阵的固有特性对其进行简化，认为除附加质量系数矩阵对角线上的系数处，其他都取0值，得到：
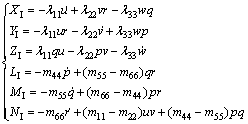(7)
可见：确定惯性类水动力的主要工作是确定上式中的6个附加质量，即λ11，λ22，λ33，λ44，λ55和λ66。
2 附加质量计算
2.1 Hess-Smith方法
20世纪60年代，美国的Hess和Smith发展了1种计算任意三维物体势流的方法[14]。这一方法称为Hess-Smith方法。它是指用许多平面四边形表面单元(鳞片)近似表示物面，每个单元上布置一个强度未知的源，然后，在物体表面的某些考察点上满足法向速度为零的物面边界条件，得到求单元源密度的线性代数方程组，求解方程组得到源密度分布，进而可求流场内任意点的速度、压力等物理量。其控制方程(拉普拉斯方程)为：
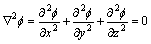(8)
边界条件为：
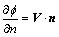，在物面上 (9)
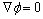，无穷远处 (10)
其中：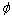
为扰动速度势；n为物面上表面单位法向矢量；V为滑行艇的运动速度。
由基本流体力学知识可知附加质量定义为：
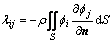
(11)
由附加质量定义式可以看出：计算附加质量的关键就是计算势函数。为了计算复杂形状物体绕流，本研究采用格函数法。在具体的数值求解过程中，应用Hess-Smith方法计算三维物体的势流。理想流体的物面边界条件可以表示为：
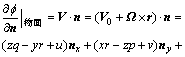
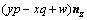(12)
其中：nx，ny和nz分别为船舶表面的单位外法向矢量n在随体坐标系中在x，y和z方向上的3个分量；x，y和z分别为流场中任一点处的矢径r的3个分量。
根据势流叠加原理及克希霍夫方法，速度势函数可用船舶运动速度、角速度及单位速度势函数表示为：
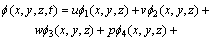
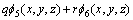(13)
其中：
，
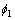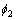和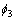
分别表示x，y和z方向平移运动的单位速度势函数；
，
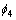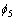和
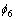分别表示x，y和z方向旋转运动的单位速度势函数。
将式(12)代入式(11)中，考虑到u，v，w，p，q和r的任意性，可以得到：
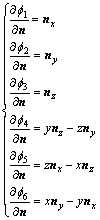(14)
设船舶表面被划分成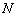
个四边形单元，则
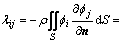
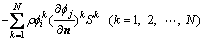(15)
式中：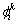
为船舶仅有第i个分速时，物面第k个单元上的速度势；
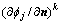为飞艇仅有第j个分速时，物面第k个单元上的法向分速；Sk为第k个单元的面积。
求解上式即可得到附加质量。其数值计算过程 为：提出流场问题—确定积分方程—数值离散—单元平面化—影响系数计算—编制程序计算势函数和表面速度，求出附加质量的数值解。本研究中的Hess-Smith方法实现过程如下：首先，选用Solid Edge软件对结构物进行建模，然后，以ASCⅡ格式输出中间文件；然后，使用GAMBIT软件对结构物进行建模和网格离散，提取生成的面网格文件进行处理，生成适合计算的面元网格格式文件并输出以GENERIC为求解器的*.neu网格文件，网格划分作为人为因素影响最大的部分是至关重要的一步，本研究采用结构网格方法对无人艇湿表面进行网格划分，针对不同曲率的表面可选择适当的单元类型和排列方式；最后，利用C语言编制程序实现直接读取节点信息和单元信息中的单元编号和节点排序，并根据面元网格格式输出到Hess- Smith可识别的dat格式文本文件，利用Hess-Smith方法编制程序计算三维物体的附加质量。
2.2 椭球算例
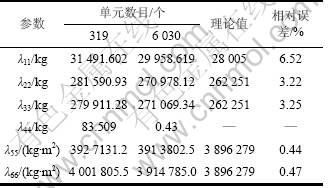
首先计算任意一椭球体(2a=20 m，2b=2c=5.33 m，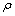
=1.225 kg/m3)的附加质量。本研究直接给出计算结果，并将其与理论值[15]进行了比较(见表1)，可以看出计算结果与理论值吻合得很好，λii(i=1,···, 4)最大相对误差为6.52%，λ55和λ66中，最小相对误差仅为0.44%，表明本研究用于计算附加质量的方法是正确的，程序是可靠的。由计算结果可以看出，Hess-Smith方法计算的结果随网格的精细而精准并趋近真实，认为5 000网格就完全能够满足精度要求。
表1 椭球体附加质量结果比较
Table 1 Comparative results of ellipsoid added mass
2.3 经验公式计算无人艇附加质量
根据文献[15]中的经验公式计算某型无人艇的附加质量，实船主尺度如下表2所示，计算结果见表3。
图2 无人艇三维建模
Fig.2 Three-dimensional model of USV
表2 实船主尺度
Table 2 Main parameters of USV
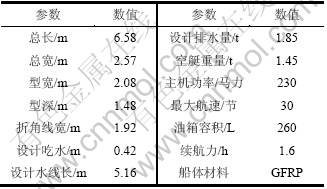
表3 经验公式计算结果
Table 3 Results of empirical formula
2.4 Hess-Smith法计算无人艇附加质量
当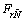＞3.0时船舶处于滑行状态，即当速度大于10 m/s时，本无人艇开始滑行。对其进行缩尺比为2.5的模型试验，该试验采用自由拖曳法测试了船模阻力、升沉和纵倾角等参数，船模见图3。其中阻力采用电测法测量，纵倾角采用倾角传感器测量，升沉采用升沉仪测量测得。纵倾角及升沉等状态参数换算为实船后如表4所示。
图3 无人艇模型图片
Fig.3 Picture of the USV
根据Gambit软件划分四面体单元格(典型网格划分见图4和图5)，并输出单元坐标，节点信息分为4列，其中第1列为节点编号，后3列为节点坐标。单元信息按照单元类型分为6列(三角形单元)或7列(四边形单元)，第1列为单元编号，第2和第3列为单元格式说明，后几列为节点序号的排列。然后，根据Hess-Smith法编程计算船舶速度势及附加质量，读入的网格信息经过C语言编制程序重新读取，面元信息为节点坐标点，共12列。当艇在水中是，密度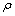= 1 025.22 kg/m3，其艇体入水参数如表5所示，计算结果见表6。
表4 无人艇航行纵倾角及升沉
Table 4 Trim angle and draft of USV
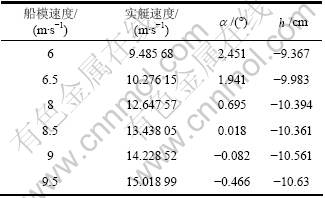
图4 低速时船体入水形状及网格划分
Fig.4 Water entry shape and grid of USV at slow speed
图5 高速时船体入水形状及网格划分
Fig.5 Water entry shape and grid of USV at high speed
表5 艇体入水参数
Table 5 Water entry parameters of USV
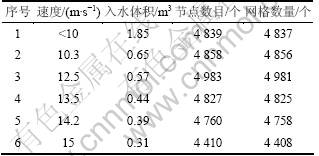
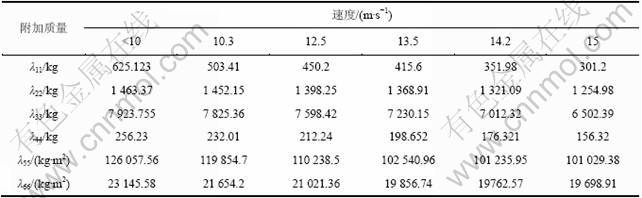
表6 Hess-Smith方法计算结果
Table 6 Results of Hess-Smith method
3 仿真实验及对比分析
无人艇海试实艇航速试验进行顺风、逆风2次，往返测量尽量保持同一航线，测量起止点也应尽量保持一致。测速时，航向保持不变。航速使用GPS进行测量，由艇上无线电单元及岸上无线电单元传输数据，进行实时监控记录。该无人艇海试图片如图6所示。
图6 无人艇实船海试图片
Fig.6 Sea-experiment picture of USV
根据上文中的6自由度方程，运用4阶定步长龙格-库塔(Rung-Kutta)法进行数值求解，从而求得无人艇任意时刻的加速度。然后，对加速度进行数值积分，获得任意时刻的位置和速度，进而预报其运动状态。在其他参数保持一致，给定推力(发动机3 000 r/min)的情况下，分别仿真2种不同附加质量情况下的无人艇加速过程，记录状态参数u随时间节拍的变化，每0.5秒记录1次数据以保证和实艇海试数据相同节拍。其具体比较结果见图7。
通过图7中3种加速过程的对比可以看出：在不同的附加质量情况下，得到的状态参数不一样，附加质量对无人艇的运动状态有一定影响。考虑不同航速下的航行状态是必要的，其仿真结果更加接近真实情况。
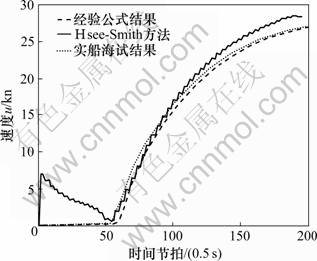
图7 附加质量结果对比
Fig.7 Comparison of accelerated motion of USV
4 结论
(1) 通过Hess-Smith方法编写的三维物体在流体中的附加质量计算程序可靠。
(2) 附加质量对无人艇的运动状态有一定影响，尤其是滑行艇的附加质量计算。考虑不同航速时入水形状有所变化是必要的，其结果较经验公式更接近真实情况。
(3) 由于海上实际情况复杂多变，风浪流的影响是不可避免的，在进行仿真时忽略了这些外力，可能导致在与实际数据之间有所偏差。
(4) 通过Hess-Smith方法计算滑行艇附加质量时，忽略了水上部分产生的附加质量，也可能使得计算值产生了一些误差。
参考文献：
[1] US Department of the Navy. The Navy Unmanned Surface Vehicle (USV) Master Plan[R]. Washington D C: US Department of the Navy, 2007.
[2] 徐玉如, 苏玉民, 庞永杰. 海洋空间智能无人运载器技术发展展望[J]. 中国舰船研究, 2006, 1(3): 2-4.
XU Yu-ru, SU Yu-min, PANG Yong-jie. Expectation of the development in the technology on ocean space intelligent unmanned vehicles[J]. Chinese Journal of Ship Research, 2006, 1(3): 2-4.
[3] MANLEY J E. Autonomous surface vessels, 15 years of development[C]//Proceedings of the Oceans 2008 MTS/IEEE Quebec Conference and Exhibition. Quebec, 2008: 1-4.
[4] VEERS J, BERTRAM V. Development of the ASV multi- mission surface vehicle III[C]//Proceedings of 5th Int Conf Computer and IT Application in the Maritime Industries. COMPIT. Delft, 2006: 345-355.
[5] Caccia M, Bibuli M, Bono R, et al. Basic navigation, guidance and control of an unmanned surface vehicle[J]. Autonomous Robots, 2008, 25: 349-365.
[6] Xu T, Chudey J, Sutton R. Soft computing design of a multisensory data fusion system for unmanned surface vehicle navigation[C]//Proceedings of 7th IFAC Conference Maneuvering Control of Marine Craft. Lisbon, 2006: 124-156.
[7] Faltinsen O M. Hydrodynamics of high-speed marine vehicles [M]. New York: Cambridge University Press, 2005: 342-385.
[8] 马烨, 单雪雄. 数值计算复杂外形物体附加质量的新方法[J]. 计算机仿真, 2007, 24(5): 75-78.
MA Ye, SHAN Xue-xiong. A new numerical computation method for added masses of complicated object[J]. Computer Simulation, 2007, 24(5): 75-78.
[9] 许维德, 林建国. 细长回转体附加质量的数值计算[J]. 水动力学研究与进展, 1986, 1(2): 70-81.
XU Wei-de, LIN Jian-guo. Numerical calculation of added masses of slender bodies of revolution[J]. Journal of Hydrodynamics, 1986, 1(2): 70-81.
[10] 吴望一. 流体力学[M]. 北京: 北京大学出版社, 2000: 154-166.
WU Wang-yi. Fluid Mechanics[M]. Beijing: Peking University Press, 2000: 154-166.
[11] 朱仁传, 郭海强, 缪国平, 等. 一种基于CFD 理论船舶附加质量与阻尼的计算方法[J]. 上海交通大学学报, 2009, 43(2): 198-203.
ZHU Ren-chuan, GUO Hai-qiang, MIAO Guo-ping, et al. A computational method for evaluation of added mass and damping of ship based on CFD theory[J]. Journal of Shanghai Jiaotong University, 2009, 43(2): 198-203.
[12] Chang H X, Miao G P, Liu Y Z. Numerical simulation of viscous flow around a rolling cylinder with ship like section[J]. China Ocean Engineering, 1995, 9 (1): 9-18.
[13] 邵世明, 王云才. 高速艇动力学[M]. 上海: 上海交通大学出版社, 1990: 1-5.
SHAO Shi-ming, WANG Yun-cai. Hydrodynamics of high-speed vehicles[M]. Shanghai: Shanghai Jiaotong University Press, 1990: 1-5.
[14] Hess J L, Smith A M O. Calculation of potential flow about arbitrary bodies[J]. Progress in Aeronautical Science, 1967, (8): 1-133.
[15] 王小宁, 陆文理. 滑行艇动稳性[J]. 国外舰船工程, 1998, 231: 11-18.
WANG Xiao-ning, LU Wen-li. Dynamic stability of planning vessels[J]. Ship Engineering Abroad, 1998, 231: 11-18.
(编辑 何运斌)
收稿日期：2011-04-15；修回日期：2011-06-15
基金项目：水下智能机器人技术国防科技重点实验室开放课题研究基金资助项目(2008003)；国家自然科学基金资助项目(61004008)
通信作者：孙寒冰(1985-)，女，黑龙江五常人，博士研究生，从事无人水面艇的水动力计算及操纵运动方向研究；电话：13796629437；E-mail: sun-han-bing@163.com
