Risk assessment of floor water inrush in coal mines based on MFIM-TOPSIS variable weight model
来源期刊:中南大学学报(英文版)2021年第8期
论文作者:薛翊国 苏茂鑫 张贯达 柏成浩 张开 陶宇帆
文章页码:2360 - 2374
Key words:floor water inrush; risk assessment; multi-factor interaction matrix (MFIM); technique for order performance by similarity to ideal solution (TOPSIS); variable weight
Abstract: Floor water inrush is one of the main types of coal mine water hazards. With the development of deep mining, the prediction and evaluation of floor water inrush is particularly significant. This paper proposes a variable weight model, which combines a multi-factor interaction matrix (MFIM) and the technique for order performance by similarity to ideal solution (TOPSIS) to implement the risk assessment of floor water inrush in coal mines. Based on the MFIM, the interaction between seven evaluation indices, including the confined water pressure, water supply condition and aquifer water yield property, floor aquifuge thickness, fault water transmitting ability, fracture development degree, mining depth and thickness and their influence on floor water inrush were considered. After calculating the constant weights, the active degree evaluation was used to assign a variable weight to the indices. The values of the middle layer and final risk level were obtained by TOPSIS. The presented model was successfully applied in the 9901 working face in the Taoyang Mine and four additional coal mines and the results were highly consistent with the engineering situations. Compared with the existing nonlinear evaluation methods, the proposed model had advantages in terms of the weighting, principle explanation, and algorithm structure.
Cite this article as: ZHANG Guan-da, XUE Yi-guo, BAI Cheng-hao, SU Mao-xin, ZHANG Kai, TAO Yu-fan. Risk assessment of floor water inrush in coal mines based on MFIM-TOPSIS variable weight model [J]. Journal of Central South University, 2021, 28(8): 2360-2374. DOI: https://doi.org/10.1007/s11771-021-4775-x.

J. Cent. South Univ. (2021) 28: 2360-2374
DOI: https://doi.org/10.1007/s11771-021-4775-x
ZHANG Guan-da(张贯达)1, XUE Yi-guo(薛翊国)1, BAI Cheng-hao(柏成浩)1,SU Mao-xin(苏茂鑫)1, ZHANG Kai(张开)1, TAO Yu-fan(陶宇帆)1, 2
1. Geotechnical and Structural Engineering Research Center, Shandong University, Jinan 250061, China;
2. Department of Mining Engineering, Colorado School of Mines, Golden, CO 80401, USA
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2021
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2021
Abstract: Floor water inrush is one of the main types of coal mine water hazards. With the development of deep mining, the prediction and evaluation of floor water inrush is particularly significant. This paper proposes a variable weight model, which combines a multi-factor interaction matrix (MFIM) and the technique for order performance by similarity to ideal solution (TOPSIS) to implement the risk assessment of floor water inrush in coal mines. Based on the MFIM, the interaction between seven evaluation indices, including the confined water pressure, water supply condition and aquifer water yield property, floor aquifuge thickness, fault water transmitting ability, fracture development degree, mining depth and thickness and their influence on floor water inrush were considered. After calculating the constant weights, the active degree evaluation was used to assign a variable weight to the indices. The values of the middle layer and final risk level were obtained by TOPSIS. The presented model was successfully applied in the 9901 working face in the Taoyang Mine and four additional coal mines and the results were highly consistent with the engineering situations. Compared with the existing nonlinear evaluation methods, the proposed model had advantages in terms of the weighting, principle explanation, and algorithm structure.
Key words: floor water inrush; risk assessment; multi-factor interaction matrix (MFIM); technique for order performance by similarity to ideal solution (TOPSIS); variable weight
Cite this article as: ZHANG Guan-da, XUE Yi-guo, BAI Cheng-hao, SU Mao-xin, ZHANG Kai, TAO Yu-fan. Risk assessment of floor water inrush in coal mines based on MFIM-TOPSIS variable weight model [J]. Journal of Central South University, 2021, 28(8): 2360-2374. DOI: https://doi.org/10.1007/s11771-021-4775-x.
1 Introduction
To date, the average mining depth of coal mines in production worldwide has been increasing [1]. During this process, coal mine water hazards frequently occurred. Although huge casualties would not be caused like gas accidents and coal dust explosions, the economic losses caused by water hazard are far greater than the other two once it occurs. Among them, floor water inrush, one of the most important types of coal mine water hazards, had a great impact on engineering security [2]. For example, on October 26, 2002, a serious water inrush accident occurred in the 21102 working face of the 17th coal seam in the Sanhejian Mine in Jiangsu Province, China; this event had a maximum instantaneous water inflow reaching 2170 m3/h, with an average water inflow of 1020 m3/h [3]. In March 10, 2007, a floor water inrush accident occurred in the Laohutai Mine in Liaoning Province, resulting in the deaths of 24 miners and the whereabouts of 5 miners were unknown [4]. On August 17, 2010, a water inrush accident through a fault with a high flow rate that occurred at the 8602 working face of Taizhuang Mine in Shandong Province caused substantial economic losses; fortunately, there were no casualties [5]. On May 22, 2017, a serious water inrush from the coal seam floor occurred in Qingxu Mine in Shanxi Province, resulting in 11 people being trapped [6]. As coal mining continues to extend to the great depths and the mining intensity increases, floor water inrush has increasingly become a major problem that plagues the sustainable development of coal mines.
Many studies using theoretical analysis and numerical simulation have been performed on the principle and prediction of coal seam floor water inrush. TIAN [7] proposed the defects of the water inrush coefficient and further revised the formula based on the analysis of the water inrush coefficient applied in engineering. By combining the water inrush coefficient and the geological structure index, a modified water-inrush coefficient calculation model is established to reasonably predict the floor water inrush [8]. SUN et al [9] analyzed the formation and evolution process of water channels from coal floors by using COMSOL software and the effect of geological structures, especially faults, on floor water inrush was obtained. The floor’s change in the stress field, displacement field and plastic zone in the mining process was numerically simulated, the whole process of rheological failure was reproduced, and the maximum disturbance depth of the floor was obtained [10]. However, the previously proposed theoretical calculation formulas of floor water inrush evaluation were partial or empirical, and often only a few influence factors were considered, which were not suitable for more coal mines. Despite the rapid development of numerical calculation methods, the complex geological and hydrogeological conditions faced by deep mining still cannot be effectively simulate.
In addition, based on nonlinear statistical theory, risk assessment methods and prediction models of floor water inrush have been considered from multiple angles. A floor water inrush evaluation method of the vulnerability index based on the analytic hierarchy process (AHP) and geographic information system (GIS) was applied in engineering and good evaluation results were obtained [11]. ZHANG et al [12] used the entropy method and the AHP to carry out subjective and objective comprehensive weight assignment, and established a fuzzy comprehensive evaluation model for floor water inrush to make it more realistic. LI et al [13] took both qualitative and quantitative indicators into account and proposed an attribute synthetic evaluation system based on the attribute mathematical theory and the AHP. To overcome the uncertainty among the indices, the risk assessment of coal floor water inrush was carried out through grey relational analysis (GRA) and the AHP [14]. WU et al [15] combined Scenario analysis methodology and Bayesian networks to develop an assessment framework for the probability of water inrush in coal mines. The variable weight method (VWM) was introduced into the calculation of the vulnerability index, and the proposed variable weight evaluation model of water inrush overcame the deficiency of the constant weight method [16]. WANG et al [17] established a prediction model for evaluating the potential of mine water inrush on the basis of fractal theory and an improved AHP. Principal component logistic regression analysis (PCLRA) was combined with the GIS and a mathematical model for predicting floor water inrush was established, which aimed to improve the fitting degree [18]. QU et al [19] established a multiple nonlinear regression modified model for predicting the maximal water bursting discharge from the coal seam floor, based on the optimal univariate nonlinear regression analysis. Similarly, the collaboration-competition theory was also introduced into the research on the risk assessment of floor water inrush [20]. WANG et al [21] took the uncertainty of evaluation indices into consideration and proposed a nonlinear fuzzy interval method to evaluate the risk level of coal floor water inrush. In fact, the complex geological environment in which coal mines are located is an integral system, and various geological and hydrogeological conditions influence each other and have extremely complex relationships. In the past risk assessment of floor water inrush, the weighting method adopted was relatively monotonous and did not consider the influence of the interaction of various factors on the water inrush. Most of them used the constant weight method, which could only evaluate a class of subjects with similar influences.
To improve the existing deficiencies, this paper proposes a variable weight model for the risk assessment of coal seam floor water inrush based on the MFIM and TOPSIS. The interaction between the evaluation indices and their influence on floor water inrush can be considered by using the theory of the MFIM, which is more scientific and reasonable. Through improving the active degree evaluation criterion, the assignment of a variable weight is achieved. To improve the accuracy of the evaluation results, an intermediate layer is added to the risk classification. First, it is necessary to rationally select the evaluation indices of floor water inrush and determine the risk levels. Then, the constant weight of each index is determined by coding the MFIM and the variable weights are assigned in light of the active degree values. Finally, the risk levels of floor water inrush are calculated with the TOPSIS method in engineering applications. The variable weight model is applied to evaluate the risk of floor water inrush in the Taoyang Mine and four additional coal mines.
2 Method
2.1 Multi-factor interaction matrix
All relevant factors in rock engineering play roles not in fixed collocation and isolation, but in a dynamic process of interaction and influence. HUDSON [22] proposed the rock engineering system (RES) theory, which not only considers the influence of each parameter on the entire system, but also studies the contribution of the interaction between the parameters to the entire system. The MFIM, an important part of RES theory, is used to describe and analyze the importance of factors in the system. SHANG et al [23] introduced MFIM to engineering geology and solved the problem of selecting the location of a pumped storage hydropower station in China. The MFIM was also applied to the risk assessment of tunnel collapse and an effective prediction method was established [24]. HUANG et al [25] used MFIM to present a method of automated zonation and classification of the rock mass. FARAMARZI et al [26] built a rock blasting fracture prediction model based on the RES, and its effectiveness was proven by making a comparison with other models. The MFIM method mainly includes three processes: 1) code the matrix of multi-factor interactions; 2) calculate the degree of the active and passive effects of each influence factor; and 3) assign the weights of influence factors.
2.1.1 Coding interaction matrix
Assuming that an evaluation object has n influence factors, an MFIM can be constructed after considering the interactions between every two factors. The first step of the method is to place the n influence factors on the main diagonal of the matrix (the order of front and back can be interchanged). The positions outside the main diagonal of the matrix are filled in with code V, which uses five-level codes to describe the strength of the influence factors’ pairwise interaction, indicating no interaction (0), weak interaction (1), medium interaction (2), strong interaction (3) and extremely strong interaction (4). The code on the non-main diagonal of each row indicates the influence of the factor of the main diagonal on the other factors, namely, the active effect. The code on the non-main diagonal of each column indicates the influence of the factor of main diagonal affected by other factors, namely, the passive effect. For instance, Vij (i≠j) not only represents the active effect of factor i on factor j in the horizontal direction, but also shows the passive effect that factor j has on factor i in the vertical direction. Thus, the matrix of multi-factor interaction is asymmetric, as shown in Figure 1.
2.1.2 Calculating degree of active and passive effects
The degree of the active and passive effects of influence factor i can be calculated according to the following formula:
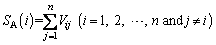 (1)
(1)
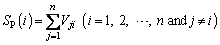 (2)
(2)
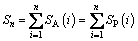 (3)
(3)
where n is the number of influence factors; SA(i) and SP(i) are the degree of the active effect and passive effect of factor i in the MFIM, respectively; and Sn is the sum of the degree of the active effect or of passive effect for all influence factors.
SA(i) is the sum of the codes in the row where the influence factor i on the main diagonal of the matrix is located, representing the degree of the active effect of factor i on other factors in the research object. SP(i) is the sum of the codes in the column where factor i is located, and shows the degree of the passive effect of factor i influenced by all other factors.
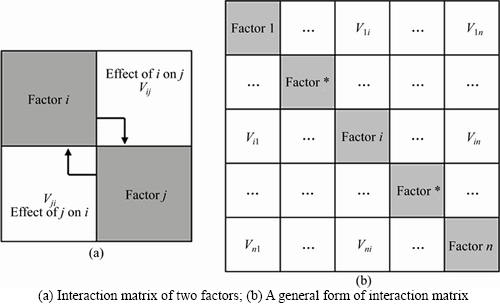
Figure 1 Multi-factor interaction matrix:
2.1.3 Weight assignment
Due to the complexity and diversity of engineering geological conditions, the same influence factor has various levels of activity and has different effects on the research object under different time and space conditions. The constant weight cannot reflect the influence of the dynamic change of the factors. As a result, it is necessary to evaluate the active degree of each factor before the weight calculation. The active degree is an evaluation coefficient that indicates how prominent the parameter is relative to the general level of the system. For a data set that has been classified, if the classification of a parameter is much greater than the similar classification of other parameters which represents general level, then the active degree of this parameter is considered to be large. LI et al [27] took the engineering geological conditions into account, made evaluation of the active degree of every factor and assigned the variable weights in the site selection for the China Spallation Neutron Source (CSNS) project. In this study, a reasonable evaluation of the active degree is important for performing a variable weight distribution of the factors. The constant weights and the variable weights can be calculated using Eqs. (4) and (5), respectively.
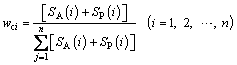 (4)
(4)
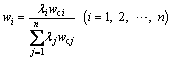 (5)
(5)
where wci and wi are the constant weight and variable weight of factor i; λi and λj are the active degree values of factor i and j, respectively.
The VWM based on the active degree evaluation not only considers the impact of the interaction between various influence factors on the overall system, but also reflects the impact of the same factor internal differences on the system. This consideration makes the weight allocation more objective, accurate and time-sensitive.
2.2 Technique for order performance by similar to ideal solution
As a scientific and reasonable comprehensive evaluation method, TOPSIS is suitable for dealing with decision-making problems with multiple factors and multiple objects [28]. This method has been widely applied in the field of geotechnical engineering, such as coal mine safety evaluation [29], risk prediction of water inrush and mud gushing in tunnels [30], rockburst tendency prediction model building [31], high slope stability evaluation [32] and rock mass quality classification [33].
The principle of TOPSIS is to first find the idealized target, including an ideal solution and an anti-ideal solution. For a limited number of evaluation indices, the pros and cons of the research objects are evaluated on the basis of sorting according to the closeness of the indices to the idealized target. The research object with the best evaluation should be the closest to the ideal solution and the farthest to the anti-ideal solution.
2.2.1 Construction of standardized decision matrix
Assume that a multi-factor decision problem has n evaluation indices and m options to be evaluated. The values of the evaluation indices form an initial decision matrix (Eq. (6)), and the directionality of the evaluation indices needs to be considered in the matrix. For the benefit indices, the greater the values are, the more ideal the evaluation object will be. For the cost indices, the smaller the values are, the more ideal the evaluation object will be.
 (6)
(6)
Since the dimensions of the evaluation indices are different, it can easily affect the accuracy of the evaluation results so it is necessary to normalize the evaluation indices. Here, the 0-1 standard transformation method is selected to eliminate the dimensional differences between different indices.
For the benefit indices, the normalization formula is:
 (7)
(7)
For the cost indices, the normalization formula is:
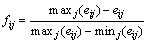 (8)
(8)
Through the formulas above, the standardized decision matrix F=(fij)m×n is constructed. In this matrix, the values of all indices are distributed in the interval [0, 1], and all indices have become benefit indices.
2.2.2 Decision evaluation
When the values of the indices and the evaluation of the pros and cons of the indices are distributed according to the linear law, the ideal solution matrix and the anti-ideal solution matrix are obtained, respectively, by
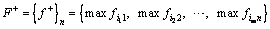
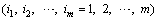 (9)
(9)

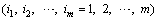 (10)
(10)
where f + and f - are the ideal solution and anti-ideal solution of each evaluation index, and the ideal solution and anti-ideal solution are the maximum and minimum values of each index in the standardized decision matrix, respectively.
Similarly, the original data of the research object also need to be normalized according to the 0-1 standard transformation method and a dimensionless array X={x1, x2, …, xn} is obtained.
This study uses the Euclidean distance to describe the pros and cons of the research object and guide decisions by calculating the closeness between the research object and the ideal solution. The weight values of the evaluation indices W={w1, w2, …, wn} need to be applied in the calculation process.
The formula for calculating the distance between the research object and the ideal solution is
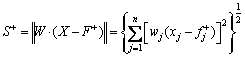 (11)
(11)
The formula for calculating the distance between the research object and the anti-ideal solution is
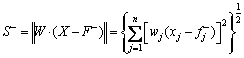 (12)
(12)
When the distance between the research object and the ideal solution is at a minimum (S+→min), and the distance between the research object and the anti-ideal solution is at a maximum (S-→max), it can be considered that the evaluation result of the research object is optimal. In previous studies, the evaluation criterion of the closeness degree is usually used to indicate the closeness of the research object to the ideal solution. However, the evaluation criterion of the closeness degree is not appropriate for the variable weight model in this article.
To effectively combine the VWM with TOPSIS, a new evaluation standard for TOPSIS is proposed. The absolute distance between the research object and the evaluation level i is taken as the evaluation coefficient, Di, calculated as
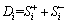 (13)
(13)
where Di is the absolute distance coefficient. The smaller the Di is, the greater the closeness to the evaluation level i is and the higher the probability of belonging to the evaluation level i is. Si+ and Si- represent the distance of the research object to the ideal solution and anti-ideal solution of evaluation level i, respectively.
3 Establishment of risk assessment model for floor water inrush
As an important engineering geological disaster with an extremely complex occurrence mechanism, floor water inrush has many influence factors, involving geological, hydrogeological, and mining conditions. Taking previous research into consideration [13, 34-36], here seven important factors were selected, namely, the confined water pressure, water supply condition and aquifer water yield property, floor aquifuge thickness, fault water transmitting ability, fracture development degree, mining depth and mining thickness. The implementation steps include: (1) list the water inrush risk classification of each influence factor as the basis for establishing a risk evaluation model; (2) assign weights to all factors based on the MFIM; and (3) use the known weight values and TOPSIS to establish the variable weight model for risk evaluation of floor water inrush.
3.1 Evaluation index and risk level
In all disaster risk assessments, the selection of evaluation indices is particularly essential. The selection of evaluation indices should follow the principles of comprehensiveness, objectivity, accessibility, characterization and measurability. In particular, the principle of objectivity requires the selected indices to be representative and to objectively reflect the characteristics of the engineering geological conditions so that the evaluation results are truer and more reliable. In this study, seven factors selected to influence floor water inrush in coal mines are described as follows.
3.1.1 Confined water pressure, I1
The confined aquifer is the main source of groundwater for floor water inrush, and the confined water pressure is the driving force of floor water inrush. The hydraulic pressure makes the confined water gradually infiltrate and rise through the joints and fissures in the floor strata, and the confined water exerts a vertical pressure on the floor strata toward the coal goaf. Due to the softening and scouring effects of the confined water, the penetration process is accompanied by the generation and expansion of water channels such as cracks. When the confined water approaches the coal seam, floor water inrush may occur. However, water inrush disasters do not necessarily occur under the condition that the water level of the aquifer is higher than that of the coal seam floor. Only when the hydraulic pressure of the confined aquifer reaches a certain critical value can disasters be induced.
3.1.2 Water supply condition and aquifer water yield property, I2
The aquifer water yield property is the material basis of water inrush from the coal seam floor. The water supply condition and aquifer water yield property determine the magnitude of water inrush. The aquifer water yield property refers to the indefinite or regular water output capacity of the aquifer, which is affected by the hydrogeological conditions, geological structure and water replenishment region of the mining area. The stronger the groundwater fluidity of the aquifer is, the more developed the geological structure of the underground rock formation is, the more sufficient the groundwater recharging is, the higher the CO2 content in the water is, the more prominent the water supply condition and aquifer water yield property will be and the greater the risk of water inrush is. In previous studies, the aquifer water yield property and the water supply condition were separated, but after consideration and analysis, it is believed that they are highly correlated, so in this study, the two were combined into one evaluation index (Table 1).
3.1.3 Floor aquifuge thickness, I3
The thickness of the floor aquifuge is the distance from the bottom of the coal seam to the top of the aquifer, and is the main influence factor for restraining water inrush from the coal seam floor. In the case of other factors remaining unchanged, such as the lithology and fracture development degree, the increase in the floor aquifuge thickness helps to reduce the probability of water inrush from the floor.
3.1.4 Fault water transmitting ability, I4
The fault water transmitting ability characterizes whether the groundwater in the aquifer can migrate and its migration speed; it is an important factor affecting the occurrence of floor water inrush disasters. The strength of the fault water transmitting ability is closely related to the permeability of the rock formation and the density of the water-conducting fissures. Different rocks have different permeabilities. The greater the permeability is, the stronger the fault water transmitting ability will be. Whether the fracture can conduct water mainly depends on its connectivity. The connectivity includes the connectivity of a single fracture surface and the connectivity between different fracture surfaces. The interconnected fractures form a water-conducting network. Strong fault water transmitting ability will increase the risk of water inrush.
Table 1 Value of water supply condition and aquifer water yield property, I2

3.1.5 Fracture development degree, I5
The fracture development degree of stratigraphic rocks is usually measured by the distribution spacing, width and filling of the fractures. The floor water inrush correlates closely with the degree of fracture development. Under the effect of groundwater pressure, when the brittle rock is stressed beyond the elastic limit, the stress is mainly released in the form of a brittle fracture, whose structural fissures are developed. The fissures are longer and wider, with greater cut-through properties of rocks and less muddy fillings. In contrast, the plastic rock stress is mainly released in the form of plastic deformation after stress. The cracks are narrower, shorter and filled by mud products, with densely distributed cracks. If the degree of fracture development is high, then the fissures will develop into water storage spaces and water flow channels under the action of confined water. Further expansion of the fissures will damage the effective water-proof rock mass.
3.1.6 Mining depth, I6
The mining depth of the coal seam is an important factor under the mining conditions. The mining depth is mainly affected by the location of the minerals. As the depth increases, the initial ground stresses become larger, leading to many engineering geological problems.
3.1.7 Mining thickness, I7
The mining thickness of the coal seam also needs to be considered. Mining thickness is restricted by mineral reserves and engineering geological conditions and undesirable engineering geological conditions will limit the planned mining thickness. When the mining thickness is increased, the disturbance to the rock formation will be enlarged, which easily causes water inrush.
3.1.8 Grade of risk assessment
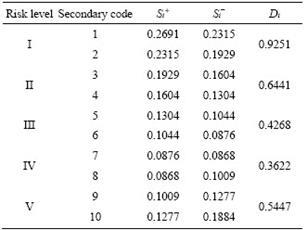
Taking previous research and experience into account, the risk of floor water inrush in coal mines is divided into five levels: I (very low risk), II (low risk), III (medium risk), IV (high risk), and V (very high risk) [21, 36-38]. The specific risk grade division of the evaluation indices is shown in Table 2. This study improved the previous risk classification by adding an intermediate layer between the risk levels and the evaluation indices, and dividing the I-V risk levels into 1-10 secondary codes to present good fineness of the index classification. For example, the risk level I includes secondary codes 1 and 2; when the values of the evaluation index and risk levels are distributed, according to a linear law, the index value belongs to the range of risk level I, the secondary code of the smaller index value is 1 and the secondary code of the larger index value is 2. The absolute distance coefficient in the risk assessment of floor water inrush is calculated by the equation D(I)=D(1)+D(2). More details are shown in the matrix of Eqs. (14).
 (14)
(14)
Table 2 Grade division and secondary code of evaluation indices
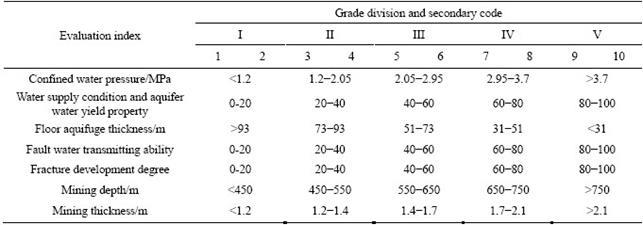
3.2 Interaction matrix of evaluation indices
The influence factors of floor water inrush in the coal mines do not work independently, but interact with each other to affect the probability and severity of water inrush. After research and analysis, two evaluation indices that seem to be unrelated, are the interactional and correlative indices. This study used the principles of the Delphi method [39], and invited multiple experts to conduct independent scoring and evaluation. Through statistical analysis, an MFIM of evaluation indices of floor water inrush is established (Figure 2).
The confined water pressure (I1) has a great influence on the formation and expansion of the water flowing channels in the rock formation, which increases the connectivity of the joints and fissures. The water supply condition and aquifer water yield property (I2) are the material basis for the generation of the groundwater pressure and the movement of groundwater in the rock stratum. The existence of a water-resisting layer is the key to preventing the occurrence of floor water inrush disasters, and this layer inhibits the confined water from approaching the coal seam. The fault water transmitting ability (I4) and fracture development degree (I5) play significant roles in floor water inrush and the two are closely related. At present, the mining depth (I6) of coal seams is gradually increasing, the hydraulic pressure of the aquifer will increase and the floor aquifuge thickness (I3) will be correspondingly reduced. The design of mining thickness (I7) is restricted by the geological and hydrogeological conditions; a large mining thickness disturbs more seriously the surrounding rock. In this study, the constant weights are calculated as Eqs. (4) according to the MFIM method, and the order of importance of the evaluation indices of the floor water inrush is I5>I4>I3>I1>I2>I6>I7.
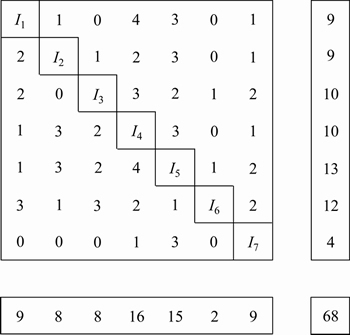
Figure 2 Multi-factor interaction matrix of evaluation indices (The upper left section includes seven evaluation indices, as well as the active effect and passive effect between the indices. The upper right section is the degree of active effect of seven indices, SA(i) and the lower left section is the degree of passive effect of these indices, SP(i), in which i=1, 2, …, 7. The lower right section is Sn, the sum of SA(i) or SP(i))
To apply the calculated constant weights to the risk assessment of engineering practice, the active degree of each evaluation index is evaluated based on field monitoring and expert scoring, and variable weight allocation is realized. Because there is almost no factor whose active degree value is 0 in floor water inrush, the old evaluation standard is too imprecise. This study optimizes the evaluation criterion for the active degree, and changes the previously used 0-1-2 criterion [27] to the 1-1.5-2 criterion (Table 3). In this criterion, the active degree values of those factors that are at a normal level are taken as 1; the more active ones are taken as 1.5; and the extremely active ones are taken as 2.
Table 3 Evaluation criteria for active degree

3.3 Computational flow of evaluation model
The TOPSIS method and its evaluation criterion are used to evaluate the risk of floor water inrush in coal mines. The computational flow of the variable weight model based on MFIM and TOPSIS is shown in detail in Figure 3.
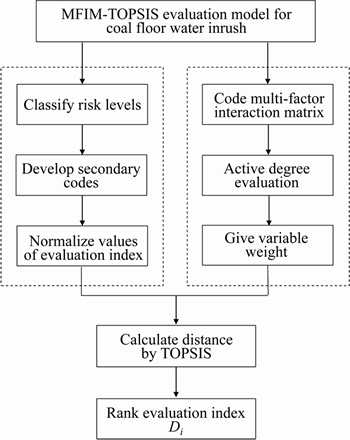
Figure 3 Diagram of MFIM-TOPSIS evaluation model
4 Engineering application
4.1 Risk assessment of floor water inrush in Taoyang Mine
This study selected the 9901 working face of the Taoyang Mine [40] as the study area. The Taoyang Mine is located in Feicheng city, Tai’an city, Shandong Province, and is an important part of the Feicheng mining area. The Taoyang Mine was completed and put into production in 1965. The original design capacity was 45×104 t per year, and it was later expanded into a medium-sized coal mine of 90 t per year. The inclined length of the 9901 working face of the Taoyang Mine is 60 m. The coal seam is 100 m underground and the mining thickness is 1.32 m. The average distance between the top of the aquifer and the bottom of the coal seam is 9 m. In this area, there is mainly a monoclinic structure leaning to the north which is composed of many faulted structures. The faults and fissures are relatively developed, and the water transmitting ability is high. The aquifer is rich in groundwater, and the water supply conditions are good. The pressure of the confined water is approximately 0.6 MPa. The evaluation indices for the risk assessment of floor water inrush based on the geological, hydrogeological and mining conditions of the working face are presented in Table 4.
Based on the interaction matrix, the constant weight of each evaluation index can be calculated by Eqs. (1)-(4), and the constant weight array was Wc={0.134, 0.127, 0.135, 0.194, 0.209, 0.104, 0.097}. The value of each index’s active degree in the study area was obtained (Figure 4) by the proposed evaluation criterion for the active degree. With constant weights and active degree values, the variable weights of the evaluation indices can be calculated using Eq. (5) and the weight distribution is shown in Figure 5.
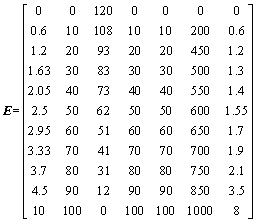
Then, according to the principle of the TOPSIS method, the initial decision matrix of the evaluation indices was listed. Here, to simplify the writing, a matrix E with eleven rows and seven columns is given as Eq. (14).
The initial decision matrix of the ideal solution, E+, was constituted by rows 1-10 of the matrix E, and rows 2-11 constituted the initial decision matrix of the anti-ideal solution, E-. The ultimate values of the evaluation indices in the matrix were obtained by comprehensively considering a wide range of coal mine engineering cases. For noncontinuous indices (such as the water supply condition and aquifer water yield property, fault water transmitting ability and fracture development degree), the ultimate value is 100, while the values of continuous indices (such as the confined water pressure, floor aquifuge thickness, mining depth and thickness) are specified in this study and shown as Eq. (15).
Table 4 Values of evaluation indices of floor water inrush
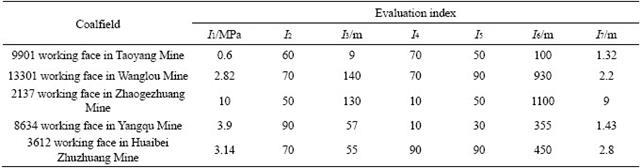
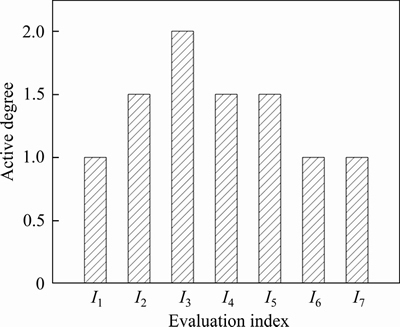
Figure 4 Active degree of each evaluation index
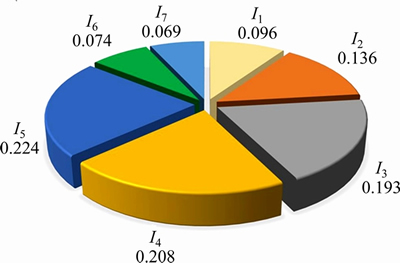
Figure 5 Variable weight values of evaluation indices
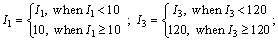
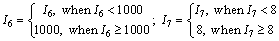 (15)
(15)
To eliminate the influence caused by the dimensional difference of the evaluation indices, the 0-1 standard transformation was carried out using Eqs. (7) and (8), and the standardized decision matrix F=(fij)11×7 was obtained. Similarly, the values of the evaluation indices needed to be normalized to obtain a dimensionless array X={0.06, 0.6, 0.925, 0.7, 0.5, 0.1, 0.165}.
For the risk level of floor water inrush, the distance to the ideal solution of each evaluation level, Si+ and the distance to the anti-ideal solution of each evaluation level, Si- were calculated according to Eqs. (11) and (12), respectively. Based on the proposed evaluation criterion for TOPSIS, the absolute distance coefficient, Di, was achieved by the expansion of Eq. (13), which can be represented as follows:
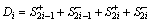 (16)
(16)
The absolute distance coefficient is in the following sequence: D(IV)
4.2 More engineering applications
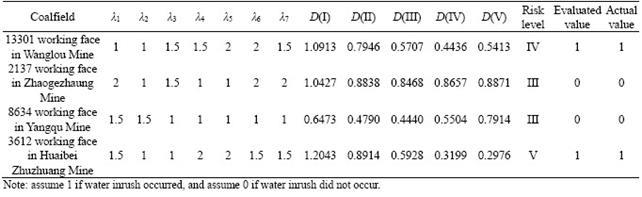
To further verify the rationality of the proposed evaluation model, more engineering case data were collected [13, 37, 42, 43], as shown in Table 4. The active degree evaluation of the indices and the results of risk assessment are listed in Table 6. The risk levels are compared with the practical conditions. The comparison results show that the evaluation results of the proposed model are very consistent with the actual situation, and the proposed model has outstanding effectiveness and operability. The variable weight model based on the MFIM and TOPSIS has practical application value in mining engineering, and can also provide a reference for risk evaluation in the engineering construction such as tunnels.
Table 5 Evaluation result of floor water inrush in Taoyang Mine
5 Discussion
5.1 Comparison with existing evaluation methods
The proposed variable weight model for the risk assessment of floor water inrush is based on the MFIM and TOPSIS method and gives full play to the outstanding advantages of the two theories. In addition, the secondary code is added to the grade division of the risk levels, which is useful for improving the accuracy of the evaluation model.
Compared with the previous theoretical formula method, the presented MFIM-TOPSIS variable weight model has greater advantages. For example, the 3612 working face in Huaibei Zhuzhuang Mine suffered a serious water inrush disaster and the evaluation level was V (Table 6); thus, the proposed model had high fitting precisions. In field monitoring, the water inrush coefficient of this working face was 0.73-0.84 [43], which exceeded the critical water inrush coefficient of 0.65. Although floor water inrush occurred, which was similar to the result of the evaluation model, the water inrush coefficient could not characterize the severity of water inrush.
To compare the accuracy and operability of various other nonlinear methods, the variable weight model proposed in this paper was compared with the fuzzy comprehensive evaluation method [21, 37], the secondary fuzzy comprehensive evaluation method [40] and the attribute synthetic method [13]. The evaluation results are listed in Table 6. For the engineering cases mentioned, all the evaluation methods had good results on whether water inrush occurred, but the risk levels were different. Except that the proposed model achieved the variable weight allocation by the MFIM, the other three methods all used the AHP to determine the weights based on the 1-9 scales method proposed by SAATY [44]. This method is a constant weight method; it neither considers the impact of the difference in evaluation indices due to the diversity of the engineering geological conditions on the risk of floor water inrush, nor did it considers the impact of the interaction of the evaluation indices on the risk assessment. In contrast, based on the MFIM and active degree evaluation, the VWM can respond well to different engineering geological conditions and can be applied to more engineering projects. Finally, both the fuzzy comprehensive evaluation method and the attribute synthetic method needed to perform a consistency check and calculate the membership degree of the evaluation indices in the algorithm, which undoubtedly greatly increased the complicated degree and workload. By comparing the specific calculation procedure of various methods, the variable weight model proposed was considered to be the most concise, effective and easy to interpret.
5.2 Weight analysis
The variable weights determined by the MFIM and active degree evaluation can more accurately and objectively reflect the impact of each evaluation factor on the floor water inrush in coal mines. Guidance for the design of the support schemes can be provided to prevent engineering disasters. For instance, the influence factor of the largest weight value, for the 9901 working face in Taoyang Mine, was the fracture development degree, plus the floor aquifuge was only 9 m. Therefore, it could be judged that the rock mass structure of the floor aquifuge at this working face was extremely unfavorable to coal mine safety, and it was wise to reinforce floor strata by grouting to strengthen the strength of the water-proof rock mass. In actual disaster control, the same measures were taken [45]. In addition, for the 2137 working face in Zhaogezhuang Mine, the confined water pressure was the index of the maximum weight value, which was 0.191. Therefore, the best supporting measures to reduce the possibility of floor water inrush were the drainage and pressure reduction, especially lowering the water table of the aquifer or causing different sizes of drawdown funnels actively and systematically.
Table 6 Evaluation results of more engineering cases
5.3 Limitation
The MFIM-TOPSIS variable weight model was applied successfully, but it still has some limitations. The MFIM was derived from the independent opinions of multiple experts. Although the Delphi method guarantees its accuracy to a certain extent, there are inevitably errors due to the differences in the level of understanding and experience of each person. The second is that some of the data obtained are too approximate, such as the water supply condition and aquifer water yield property, which is a qualitative index, reducing its effectiveness during the quantitative transformation. Valid values of evaluation indices have a very large impact on the results. In the future, the investigation of engineering geological conditions should use less descriptive statements and be directed toward quantification. In addition, the interaction of various factors and its influence on water inrush should also be studied in depth through theoretical analysis, numerical simulation and experiments.
6 Conclusions
This paper proposed a variable weight model for the risk assessment of floor water inrush in coal mines based on multi-factor interaction matrix (MFIM) and the technique for order performance by similarity to ideal solution (TOPSIS).
The risk of floor water inrush was divided into five grades. In this study, the grade division was improved by adding secondary codes between the risk levels and the evaluation indices, and the continuous and discontinuous evaluation indices were quantified and their ultimate values were limited. Here, the seven main factors of floor water inrush were considered, namely the confined water pressure, water supply condition and aquifer water yield property, floor aquifuge thickness, fault water transmitting ability, fracture development degree, mining depth and mining thickness.
The MFIM of the evaluation indices was established according to the principle of the Delphi method, the active and passive effects of each evaluation index were obtained, and then the constant weights were calculated. A new evaluation criterion of the active degree was proposed to achieve the variable weight distribution. The final evaluation results were calculated by the TOPSIS method, and the risk level of floor water inrush was determined by comparing the sizes of the absolute distance coefficients.
The MFIM-TOPSIS variable weight model for risk assessment of floor water inrush was successfully applied to the 9901 working face of Taoyang Mine, and more engineering applications were carried out. The evaluation results were in accordance with the practical situations, which verified the availability of the model. The proposed model was proven to have rationality and operability by comparing with the theoretical formula method and the other three nonlinear methods.
Contributors
The overarching research goals were developed by XUE Yi-guo, ZHANG Guan-da, and SU Mao-xin. XUE Yi-guo and BAI Cheng-hao provided the coal floor water inrush data, and analyzed the data. SU Mao-xin and BAI Cheng-hao established the evaluation model and applied it to water inrush prediction. The initial draft of the manuscript was written by ZHANG Guan-da, ZHANG Kai, and TAO Yu-fan. All authors replied to reviewers’ comments and revised the final version.
Conflict of interest
XUE Yi-guo, ZHNAG Guan-da, BAI Cheng-hao, SU Mao-xin, ZHANG Kai and TAO Yu-fan declare that they have no conflict of interest.
References
[1] ZHANG Guang-chao, HE Fu-lian, LAI Yong-hui, JIA Hong-guo. Ground stability of underground gateroad with 1 km burial depth: A case study from Xingdong coal mine, China [J]. Journal of Central South University, 2018, 25(6): 1386-1398. DOI: 10.1007/s11771-018-3834-4.
[2] SHI Long-qing, WANG Ying, QIU Mei, HAN Lu, ZHAO Yun-ping. Research in the required width of a fault waterproof coal pillar based on underground pressure control theory [J]. Arabian Journal of Geosciences, 2019, 12(15): 14. DOI: 10.1007/s12517-019-4637-0.
[3] WU Qiang, FAN Shu-kai, ZHOU Wan-fang, LIU Shou-qiang. Application of the analytic hierarchy process to assessment of water inrush: A case study for the No. 17 coal seam in the Sanhejian coal mine, China [J]. Mine Water and the Environment, 2013, 32(3): 229-238. DOI: 10.1007/s10230-013-0228-6.
[4] LI Tie, MEI Ting-ting, SUN Xue-hui, LV Yu-guo, SHENG Ji-quan, CAI Ming. A study on a water-inrush incident at Laohutai coalmine [J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 59: 151-159. DOI: 10.1016/j.ijrmms.2012.12.002.
[5] QIAN Zi-wei, HUANG Zhen, SONG Jian-guo. A case study of water inrush incident through fault zone in China and the corresponding treatment measures [J]. Arabian Journal of Geosciences, 2018, 11(14): 381. DOI: 10.1007/s12517-018-3727-8.
[6] LI S C, WU Jing, XU Z H, YANG W M. Mechanics criterion of water inrush from the coal floor under influence of fault and its engineering application [J]. International Journal of Geomechanics, 2019, 19(5): 04019022.1. DOI: 10.1061/ (ASCE)GM.1943-5622.0001387.
[7] TIAN Gan. Development and experimental research on a formula of water inrush coefficient [J]. Applied Mechanics & Materials, 2013, 448-453: 3901-3907. DOI: 10.4028/www. scientific.net/AMM.448-453.3901.
[8] SHI Long-qing, QIU Mei, WANG Ying, QU Xing-yue, LIU Tian-hao. Evaluation of water inrush from underlying aquifers by using a modified water-inrush coefficient model and water-inrush index model: A case study in Feicheng coalfield, China [J]. Hydrogeology Journal, 2019, 27(6): 2105-2119. DOI: 10.1007/s10040-019-01985-2.
[9] SUN Wen-ben, XUE Yan-chao, LI Ting-ting, LIU Wei-tao. Multi-field coupling of water inrush channel formation in a deep mine with a buried fault [J]. Mine Water and the Environment, 2019, 38(3): 528-535. DOI: 10.1007/s10230-019-00616-2.
[10] LI Ang, MA Qiang, LIAN Yan-qing, MA Li, MU Qian, CHEN Jian-bo. Numerical simulation and experimental study on floor failure mechanism of typical working face in thick coal seam in Chenghe mining area of Weibei, China [J]. Environmental Earth Sciences, 2020, 79(5): 1-22. DOI: 10.1007/s12665-020-8839-2.
[11] WU Qiang, LIU Yuan-zhang, LIU Dong-hai, ZHOU Wan-fang. Prediction of floor water inrush: The application of GIS-based AHP vulnerable index method to Donghuantuo coal mine, China [J]. Rock Mechanics & Rock Engineering, 2011, 44(5): 591-600. DOI: 10.1007/s00603-011-0146-5.
[12] ZHANG Tian-jun, REN Jin-hu, YU Sheng-hong, CUI Wei. Entropy weight-fuzzy comprehensive evaluation method of the safety evaluation of water inrush [J]. Advanced Materials Research, 2013, 868: 300-305. DOI: 10.4028/www. scientific.net/AMR.868.300.
[13] LI L P, ZHOU Z Q, LI S C, XUE Y G, XU Z H, SHI S S. An attribute synthetic evaluation system for risk assessment of floor water inrush in coal mines [J]. Mine Water and the Environment, 2015, 34(3): 288-294. DOI: 10.1007/s10230-014-0318-0.
[14] LI Bo, CHEN Yu-long. Risk assessment of coal floor water inrush from underlying aquifers based on GRA-AHP and its application [J]. Geotechnical & Geological Engineering, 2016, 34: 143-154. DOI: 10.1007/s10706-015-9935-z.
[15] WU Jian-song, XU Sheng-di, ZHOU Rui, QIN Yue-ping. Scenario analysis of mine water inrush hazard using Bayesian networks [J]. Safety Ence, 2016, 89: 231-239. DOI: 10.1016/j.ssci.2016.06.013.
[16] WU Qiang, LI Bo, CHEN Yu-long. Vulnerability assessment of groundwater inrush from underlying aquifers based on variable weight model and its application [J]. Water Resources Management, 2016, 30(10): 3331-3345. DOI: 10.1007/ s11269-016-1352-4.
[17] WANG Xin-yi, WANG Tian-tian, WANG Qi, LIU Xiao-man, LI Ren-zheng, LIU Bao-jin. Evaluation of floor water inrush based on fractal theory and an improved analytic hierarchy process [J]. Mine Water and the Environment, 2017, 36(1): 1-9. DOI: 10.1007/s10230-016-0407-3.
[18] LIU Wei-tao, LI Qiang, ZHAO Ji-yuan, FU Biao. Assessment of water inrush risk using the principal component logistic regression model in the Pandao coal mine, China [J]. Arabian Journal of Geosciences, 2018, 11(16): 463. DOI: 10.1007/s12517-018-3815-9.
[19] QU Ying-yue, QIU Mei, LIU Jin-hua, NIU Zhi-chao, WU Xiang-sheng. Prediction of maximal water bursting discharge from coal seam floor based on multiple nonlinear regression analysis [J]. Arabian Journal of Geosciences, 2019, 12(18): 567. DOI: 10.1007/s12517-019-4748-7.
[20] ZHANG Jian, WU Qiang, MU Wen-ping, DU Yuan-ze, TU Kun. Integrating the hierarchy-variable-weight model with collaboration-competition theory for assessing coal-floor water-inrush risk [J]. Environmental Earth Sciences, 2019, 78(6): 13. DOI: 10.1007/s12665-019-8217-0.
[21] WANG Xin-tong, LI Shu-cai, XU Zhen-hao, LIN Peng, HU Jie, WANG Wen-yang. Analysis of factors influencing floor water inrush in coal mines: A nonlinear fuzzy interval assessment method [J]. Mine Water and the Environment, 2019, 38(1): 81-92. DOI: 10.1007/s10230-018-00578-x.
[22] HUDSON J A. Rock mechanics principles in engineering practice [R]. CIRIA Ground Engineering Report: Underground Construction, 1989.
[23] SHANG Y J, WANG S J, LI G C, YANG Z F. Retrospective case example using a comprehensive suitability index (CSI) for siting the Shisan-Ling power station, China [J]. International Journal of Rock Mechanics and Mining Sciences, 2000, 37(5): 839-853. DOI: 10.1016/S1365-1609(00)00021-6.
[24] SHIN Hyu-soung, KWON Young-cheul, JUNG Yong-soo, BAE Gyu-jin, KIM Young-geun. Methodology for quantitative hazard assessment for tunnel collapses based on case histories in korea [J]. International Journal of Rock Mechanics and Mining Sciences, 2009, 46(6): 1072-1087. DOI: 10.1016/j.ijrmms.2009.02.009.
[25] HUANG Jian, JU Neng-pan, LI Yan-rong. Automated tunnel rock classification using rock engineering systems [J]. Engineering Geology, 2013, 156: 20-27. DOI: 10.1016/ j.enggeo.2013.01.006.
[26] FARAMARZI F, MANSOURI H, EBRAHIMI FARSANGI M A. A rock engineering systems based model to predict rock fragmentation by blasting [J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 60: 82-94. DOI: 10.1016/j.ijrmms.2012.12.045.
[27] LI Kun, SHANG Yan-jun, HE Wan-tong, LIN Da-ming, HASAN Muhammad, WANG Kai-yang. An engineering site suitability index (ESSI) for the evaluation of geological situations based on a multi-factor interaction matrix [J]. Bulletin of Engineering Geology & the Environment, 2019, 78(1): 569-577. DOI: 10.1007/s10064-017-1122-4.
[28] CLINTON J D, JACKMAN S D, RIVERS D. The statistical analysis of roll call data [J]. American Political Science Review, 2003, 98(2): 355-370. DOI: 10.1080/09546550490 446171.
[29] JAVADI M, SAEEDI G, SHAHRIAR K. Developing a new probabilistic approach for risk analysis, application in underground coal mining [J]. Journal of Failure Analysis and Prevention, 2017, 17(5): 989-1010. DOI: 10.1007/s11668-017-0325-0.
[30] WANG Ying-chao, OLGUN C G, WANG Lin-bing, MENG Bo. Risk assessment of water inrush in karst tunnels based on the ideal point method [J]. Polish Journal of Environmental Studies, 2019, 28(2): 901-911. DOI: 10.15244/pjoes/85199.
[31] XUE Yi-guo, BAI Cheng-hao, KONG Fan-meng, QIU Dao-hong, LI Li-ping, SU Mao-xin, ZHAO Ying. A two-step comprehensive evaluation model for rockburst prediction based on multiple empirical criteria [J]. Engineering Geology, 2020, 268. DOI: 10.1016/j.enggeo.2020.105515.
[32] CHEN Wen-qiang, ZHAO Yu-fei, LIU Li-ping, WANG Xiao-gang. A new evaluation method for slope stability based on TOPSIS and MCS [J]. Advances in Civil Engineering, 2020: 1-10. DOI: 10.1155/2020/1209470.
[33] WU L Z, LI Shao-hong, ZHANG Ming, ZHANG Li-min. A new method for classifying rock mass quality based on MCS and TOPSIS [J]. Environmental Earth Sciences, 2019, 78(6): 199. DOI: 10.1007/s12665-019-8171-x.
[34] MENG Zhao-ping, LI Guo-qing, XIE Xiao-tong. A geological assessment method of floor water inrush risk and its application [J]. Engineering Geology, 2012, 143: 51-60. DOI: 10.1016/j.enggeo.2012.06.004.
[35] WU Qiang, GUO Xiao-ming, SHEN Jian-jun, XU Shuang, LIU Shou-qiang. Risk assessment of water inrush from aquifers underlying the Gushuyuan coal mine, China [J]. Mine Water and the Environment, 2017, 36(1): 96-103. DOI: 10.1007/s10230-016-0410-8.
[36] LIU Wei-tao, LI Qiang, ZHAO Ji-yuan. Application on floor water inrush evaluation based on AHP variation coefficient method with GIS [J]. Geotechnical & Geological Engineering, 2018, 36(5): 2799-2808. DOI: 10.1007/s10706-018-0502-2.
[37] SUN Wen-bin, XUE Yan-chao. An improved fuzzy comprehensive evaluation system and application for risk assessment of floor water inrush in deep mining [J]. Geotechnical & Geological Engineering, 2019, 37(3): 1135-1145. DOI: 10.1007/s10706-018-0673-x.
[38] XUE Yi-guo, BAI Cheng-hao, QIU Dao-hong, KONG Fan-meng, LI Zhi-qiang. Predicting rockburst with database using particle swarm optimization and extreme learning machine [J]. Tunnelling and Underground Space Technology, 2020, 98: 103287. DOI: 10.1016/j.tust.2020.103287.
[39] ROWE G, WRIGHT G. The Delphi technique as a forecasting tool: Issues and analysis [J]. International Journal of Forecasting, 2013, 15(4): 353-375. DOI: 10.1016/S0169-2070(99)00018-7.
[40] WANG Yi, YANG Wei-feng, LI Ming, LIU Xi. Risk assessment of floor water inrush in coal mines based on secondary fuzzy comprehensive evaluation [J]. International Journal of Rock Mechanics and Mining Sciences, 2012, 52: 50-55. DOI: 10.1016/j.ijrmms.2012.03.006.
[41] QIU Mei, HAN Jin, ZHOU Yan, SHI Long-qing. Prediction reliability of water inrush through the coal mine floor [J]. Mine Water and the Environment, 2017, 36(2): 217-225. DOI: 10.1007/s10230-017-0431-y.
[42] GAO Le. Analysis on water bursting source and channel at 13301 working face of Wanglou coal mine [J]. Shandong Coal Science and Technology, 2014(8): 162-163. DOI: 10.3969/j.issn.1005-2801.2014.08.71. (in Chinese)
[43] LI De-zhong, MAO Chuan-sen, ZHU Le-zhang. Causes and comprehensive prevention of floor water inrush in No. 6 coal mine [J]. Energy Technology and Management, 2006(6): 71-73. DOI: 10.3969/j.issn.1672-9943-B.2006.06.031. (in Chinese)
[44] SAATY T L. How to make a decision: The analytic hierarchy process [J]. European Journal of Operational Research, 1990, 48(1): 9-26. DOI: 10.1016/0377-2217(90)90057-I.
[45] YIN Wan-cai, YIN Zeng-de, SHI Long-qing. Causes of mine water inrush and its prevention [J]. Journal of Jiaozuo Institute of Technology, 1999(1): 3-5. DOI: 10.3969/j.issn.1673-9787.1999.01.005. (in Chinese)
(Edited by YANG Hua)
中文导读
基于MFIM-TOPSIS变权模型的煤层底板突水风险评价
摘要:煤层底板突水是最为常见的煤矿水害类型之一,随着煤矿开采向更深部发展,底板突水风险预测与评价具有重要意义。本文提出一种煤层底板突水风险评价变权模型,有效地将多因素相互作用关系矩阵(MFIM)和理想点法(TOPSIS)结合起来。基于多因素相互作用关系矩阵,考察了7个评价指标之间的相互作用及其对底板突水的影响程度,包括承压含水层的水压力、含水层的富水性及供水条件、隔水层厚度、断层导水能力、裂隙发育程度、开采深度和开采厚度。在完成常权的计算后,利用活跃程度评价来对指标实现变权的赋予。利用已获得的权重值和理想点法理论,得到中间层的数值和最终的风险水平。所提出的模型在中国的陶阳煤矿9901工作面和其他四个煤矿得到了成功的应用,评价结果与实际情况具有较高的一致性。评价模型与现有的非线性评价方法相比,在赋权、原理解释、算法结构等方面具有优势。
关键词:底板突水;风险评价;多因素相互作用关系矩阵;理想点法;变权
Foundation item: Projects(41877239, 51379112, 51422904, 40902084, 41772298) supported by the National Natural Science Foundation of China; Project(2019GSF111028) supported by the Key Technology Research and Development Program of Shandong Province, China; Project(2018JC044) supported by the Fundamental Research Funds of Shandong University, China; Project(JQ201513) supported by the Natural Science Foundation of Shandong Province, China
Received date: 2020-08-25; Accepted date: 2020-12-27
Corresponding author: XUE Yi-guo, PhD, Professor; Tel: +86-13953166233; E-mail: xieagle@sdu.edu.cn; ORCID: https://orcid.org/ 0000-0001-9928-5947; SU Mao-xin, PhD, Associate Professor; Tel: +86-15863143113; E-mail: sumaoxin2019@163.com

