
J. Cent. South Univ. (2020) 27: 2606-2613
DOI: https://doi.org/10.1007/s11771-020-4485-9
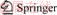
Simulation of second-order RC equivalent circuit model of lithium battery based on variable resistance and capacitance
JI Yan-ju(嵇艳鞠), QIU Shi-lin(邱仕林), LI Gang(李刚)
College of Instrumentation and Electrical Engineering, Jilin University, Changchun 130061, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Abstract: With the rise of the electric vehicle industry, as the power source of electric vehicles, lithium battery has become a research hotspot. The state of charge (SOC) estimation and modelling of lithium battery are studied in this paper. The ampere-hour (Ah) integration method based on external characteristics is analyzed, and the open-circuit voltage (OCV) method is studied. The two methods are combined to estimate SOC. Considering the accuracy and complexity of the model, the second-order RC equivalent circuit model of lithium battery is selected. Pulse discharge and exponential fitting of lithium battery are used to obtain corresponding parameters. The simulation is carried out by using fixed resistance capacitance and variable resistance capacitor respectively. The accuracy of variable resistance and capacitance model is 2.9%, which verifies the validity of the proposed model.
Key words: lithium battery; equivalent circuit model; parameter identification; SOC estimation
Cite this article as: JI Yan-ju, QIU Shi-lin, LI Gang. Simulation of second-order RC equivalent circuit model of lithium battery based on variable resistance and capacitance [J]. Journal of Central South University, 2020, 27(9): 2606-2613. DOI: https://doi.org/10.1007/s11771-020-4485-9.
1 Introduction
In recent years, with the increasing shortage of energy, energy conservation and environmental protection are promoted actively. The electric vehicle industry has achieved unprecedented development [1]. Lithium batteries have become the main energy source for electric vehicles by virtue of their superior performance [2].
The state of charge (SOC) of the battery is an important parameter for the residual energy of the reaction battery. Due to the charge and discharge characteristics of the battery, the SOC estimation during charging is much more difficult than the discharge period. Accurate and effective SOC estimation is an effective basis for battery charging and discharging strategies, and it is also the basis for evaluating battery reliability.
The battery model can reflect the state as a real battery [3], which is generally simplified by physical or mathematical methods based on the characteristics of the battery. Many classic models have been produced, such as thermal coupling model [4, 5], performance model [6, 7], and electrochemical model [8, 9]. The battery performance model is based on the external characteristics of the battery and the model is built according to the voltage and current of the battery. Because of simple modeling process, the performance model is widely used.
The network of resistors and capacitors (RC) in series and parallel can describe the external characteristics of the battery [10, 11]. Several models have been proposed, such as Rint model, Thevenin model, Massimo Ceraolo model and Fractional Order model [12-16]. The latter two models have smaller RMSE and better estimation accuracy. However, the Fractional Order model is computationally complex and difficult to apply. There are now a variety of SOC estimation methods, such as least squares, neural networks, extended Kalman filter, H∞ method, and internal resistance correction method [17-23], but they all have certain limitations.
This paper discusses the estimation of SOC, the modeling of lithium batteries, and Ah integration-open circuit voltage method. The battery parameters are simulated and identified based on the second-order RC equivalent circuit model and compared with the Battery model in the MATLAB/ Simulink environment. The effects of the fixed and variable resistance and capacitance on the estimation accuracy are analyzed, and the effectiveness of the method are verified.
2 Reference model
In order to verify the validity of the model, the battery model in MATLAB/Simulink is selected as a reference. The parameters of model and formula definitions can be found in Simulink Documentation in MathWorks [24]. The model has three ports: the positive and negative electrodes of the battery, the measurement port. The measurement port can be used to observe the real-time current, voltage and SOC of the battery. The model parameter values set in this paper are shown in Table 1.
Table 1 Basic parameters of model battery

The battery module implements a parametric representation of the most popular dynamic model of batteries. The equivalent circuit diagram of the module is shown in Figure 1.
For lithium battery types, the model uses the following formula:
Discharge model (i*>0)
 (1)
(1)
Charging model (I* < 0),
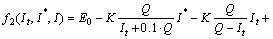
 (2)
(2)
where E0 is the constant voltage in V; K is the polarization resistance in Ω; Q is the maximum battery capacity in A·h; I* is low-frequency current dynamics in A; I is the battery current in A; It is the extracted capacity in A·h; A is the exponential voltage in V; and B is exponential capacity in A·h-1.
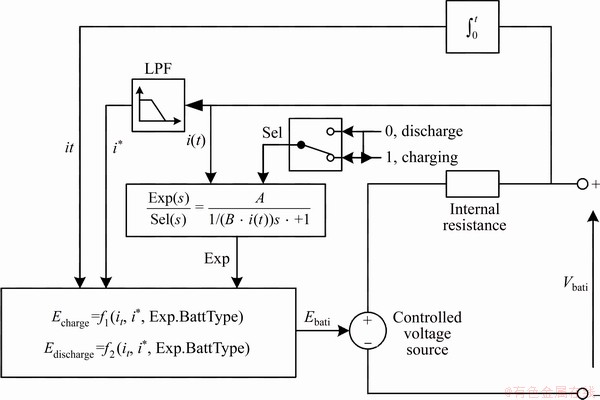
Figure 1 Battery equivalent circuit diagram of module
3 Estimation of SOC
The SOC estimation is important for the power battery, and the SOC is the key parameter for evaluating the remaining power [4]. The definition of SOC refers to the ratio of the remaining capacity to the rated capacity at a specific discharge rate.
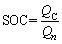 (3)
(3)
where QC is the remaining capacity, and Qn is as the rated capacity.
In practice, the remaining power is not easily measured directly, so the SOC can also be expressed as:
 (4)
(4)
where Q is the amount of discharge.
When SOC=0, it means that the battery has been completely discharged. When SOC=100%, the capacity of the battery has reached the rated capacity, that is, the battery is fully charged. The definition of SOC under different working conditions has been revised. The revised SOC is:
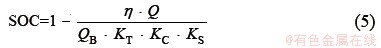
where QB is the nominal total charge of the battery; KT, KS, KC and η are the coefficient of temperature, the self-discharge rate, the cycle life, and the charge-discharge rate, respectively.
Although the lithium battery has an increase in the terminal voltage electromotive force with the increase of temperature, the influence is negligible. The temperature is set to 25 °C, that is, the temperature coefficient KT is constant.
The Ah integration method is the most common and simple method used in the SOC estimation. It does not study relatively complex chemical reactions, but uses battery current and rated capacity to estimate the remaining capacity. If the initial value SOC0 and the working time t are known, the SOC at any time, can be calculated by Eq. (6) as:

where i is the charge-discharge current; Qn is the rated capacity; and γ is the efficiency coefficient. The Ah integration method can only calculate the change value of SOC over a period of time, but cannot obtain the SOC0. It is necessary to estimate the SOC with other methods.
Excluding the influence of temperature, the relation between the OCV and the SOC of the battery is approximately determined, and the OCV is hardly affected by the battery aging, the charge and discharge rate. The open circuit voltage method uses the correspondence between the OCV and the SOC. However, the OCV of the battery needs a certain period to measure. It is not suitable for real-time estimation. Therefore, the open-circuit voltage method can be used to estimate SOC0.
Both the Ah integration method and the open-circuit voltage method have certain drawback, so the two methods can be combined. The initial value of the SOC is estimated by the open-circuit voltage method, and the current state SOC is obtained based on the integral of the current. The schematic of the Ah integration method is given in Figure 2.

Figure 2 Schematic of estimating the SOC by Ah integration method
4 Model of second-order RC equivalent circuit
According to the actual application requirements of lithium batteries, the established model should meet the following points:
1) Model parameters can be calculated;
2) The model simulation accuracy is high;
3) The order is appropriate for easy application in engineering;
4) It can reflect the static and dynamic characteristics of the lithium battery.
The Massimo Ceraolo model is selected in this paper due to its obvious advantages [25]. Since there is no parasitic phenomenon when the selected model battery is charged and discharged, the parasitic branch portion of the model is ignored. The second-order RC model has higher precision, while the third-order and fourth-order models have less precision improvement than the second-order model, and the calculation difficulty is greatly increased. The number of RC parallel branches in the Massimo Ceraolo model is 2, as shown in Figure 3. R0 is the internal resistance of the battery; Rd and Cd form the RC parallel link with small time constant, describing the rapid change process of voltage; Re and Ce form the RC parallel link with large time constant, describing the slow change process of voltage; the sum with Rd and Re can be regarded as the polarization internal resistance of the battery.
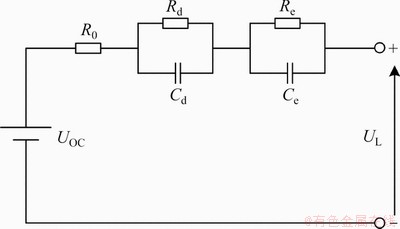
Figure 3 Second-order RC equivalent circuit model diagram
The parameter identification of the model can be divided into offline method and online method. Offline identification means that experimental data of a lithium battery have been acquired, and various parameters of the battery model are identified based on the data. Online identification is to real-time update the parameters of the battery model based on real-time information. In this paper, the parameter identification of the second-order RC equivalent circuit model is completed by exponential fitting method. The exponential fitting method relies on the pulse discharge experiment.
The initial SOC of the model battery was set as 50%. After the model battery was discharged at a current of 6.5 A for 4900 s, the voltage corresponding curve of the battery was observed. The second-order RC equivalent circuit models for offline identification and online identification are implemented as follows:
1) Offline model
The offline identification model uses fixed resistors and capacitors. The parameter identification uses an exponential fitting method. The values of the resistors and capacitors are the results of identification at a specific SOC. In the process of charging and discharging, when the SOC value of the battery is close to the setting SOC, the parameters of the resistors and capacitors in second-order RC equivalent circuit model have relatively high accuracy. At this time, the results of SOC estimation will be accurate.
2) Online model
The online identification model uses variable resistors and capacitors, and the method used for parameter identification is also an exponential fitting method. Compared with the offline identification model, the difference is that the resistance and capacitance values of the model are updated online according to the difference of the SOC.
5 Experimental results and analysis
5.1 Exponential fitting
The second-order RC equivalent circuit model is implemented in MATLAB/Simulink and the parameter identification method is simulated with the model. First, the Battery module is subjected to a pulse discharge test to obtain its SOC state. The result is shown in Figure 4.
The resistance and capacitance under different SOC are identified by exponential fitting method. The identification process is as follows:
5.1.1 Internal resistance (R0)
In the voltage and current curve shown in Figure 4, before point B, the current is zero, and the voltage curve is a smooth straight line. At this time, the battery can be considered to be in a stationary state. B-D is the discharge area, and the lithium battery is discharged at a discharge rate of 1C, where C represents the ratio of the battery charge and discharge current to the rated capacity. Therefore, the voltage at the battery terminal changes. D-F is a stationary zone, at this time, the discharge current is 0, and the discharge ends, but the response of the battery has a certain hysteresis. The OCV after point F is substantially stable.
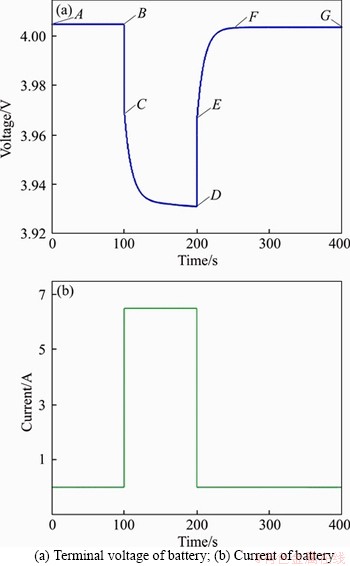
Figure 4 Pulse discharge test curve:
At points B and D, the instantaneous voltage differences are (UB-UC) and (UE-UD). In order to reduce the error in the experiment, the average value of the two voltage differences and the current ratio are taken. Calculate the ohmic internal resistance, the formula is as follows:
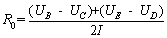 (7)
(7)
5.1.2 Polarization resistance and capacitance (Rd, Re, Cd, Ce)
In Figure 4, the current between D and F is zero and the battery discharge ends. From the perspective of the model, the presence of the RC parallel branch causes a certain lag in the response of the voltage, which can be seen as a zero-input response. Then the expression of the battery terminal voltage is as follows:
 (8)
(8)
where UOC represents the open circuit voltage;Ud(0) and Ue(0) represent the initial voltage values of the RdCd parallel branch and the ReCe parallel branch, respectively.
The D-F segment of the pulsed discharge curve was exponentially fitted according to Eq. (9) using a “Custom equations” [26] in the curve fitting toolbox cftool in MATLAB:
 (9)
(9)
Comparing Eq. (8) with Eq. (9) gives:
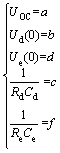 (10)
(10)
Before point B in Figure 8, the battery is in a static state, which can be regarded as a steady state. The B-D phase can be regarded as the zero-state response of the terminal voltage. The expression of the terminal voltage is as follows:
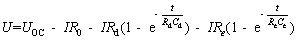 (11)
(11)
At the same time, the voltage across the capacitor is considered equal, then:
 (12)
(12)
The values of the polarization resistance and capacitance are obtained from Eqs. (10) and (12).
In order to verify the established second-order RC equivalent circuit model, the corresponding parameters are obtained according to different SOC simulations. The results are shown in Table 2.
5.2 Model analysis
To verify the established second-order RC equivalent circuit model, the pulsed discharge experiments are performed on the module [24] and the second-order RC equivalent circuit model, and their voltage response curves are compared. The simulation results are shown in Figures 5 and 6.
Figure 5 shows a comparison of the voltage response curves for the offline model. Since the resistance and capacitance values of the offline model are fixed, the magnitude of their values is the identification result at a specific SOC. It can be seen that the voltage values of the model battery and the second-order RC equivalent circuit model are close at t=2500 s. The voltage of the circuit model is lower than that of the module battery in 0-2500 s. And after 2500 s, they are exchanged. Figure 6 shows a comparison of the online model. It is obvious that the voltage response curve in the online model follows well.
This paper also analyzes the dynamic responses of the models. As shown in Figure 7, the current is set to 50% and 200% of the normal value in two discharge cycles. The relative errors of the dynamic responses of the offline model and the online model are shown in Figure 8, where the error caused by the change in current amplitude to the offline model is less than 6.2%, and the error of the online model is less than 2.9%.
Table 2 Results of parameter identification of second-order RC equivalent circuit model
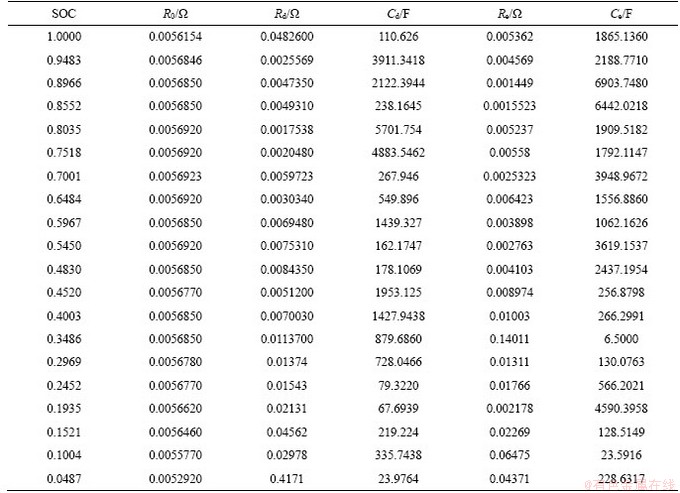
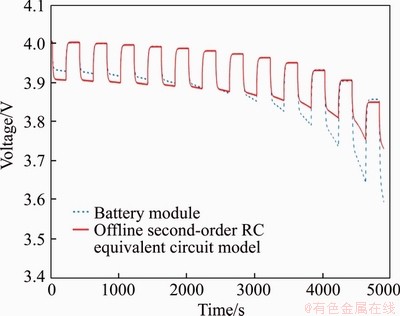
Figure 5 Comparison of voltage response curves in offline model
Both models can better track battery voltage changes, indicating that the model is accurate and effective, and the online model is better than the offline model, which improves the accuracy of modeling.
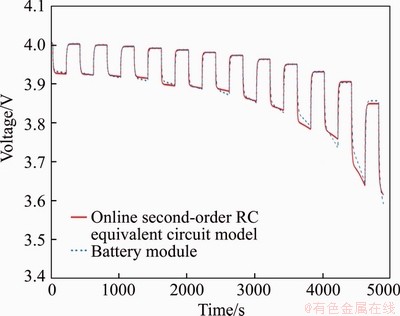
Figure 6 Comparison of voltage response curves in online model
6 Conclusions
In this paper, the estimation of SOC and the modeling of lithium battery have been proposed. The design scheme is compared and analyzed, and the simulation model is built based on MATLAB/Simulink to verify the effectiveness of the method. The SOC is estimated by the Ah integration-open circuit voltage method. Considering the complexity of the model, the accuracy and the difficulty of parameter identification, the second-order RC equivalent circuit model is selected for simulation verification. The parameter identification is performed by pulse discharge and exponential fitting method. The SOC estimation method is simulated with fixed and variable parameters of resistors and capacitors in the model. The accuracy of the fixed resistor- capacitor model can reach 6.2%, and the accuracy of the variable resistor-capacitor model can be 2.9%.
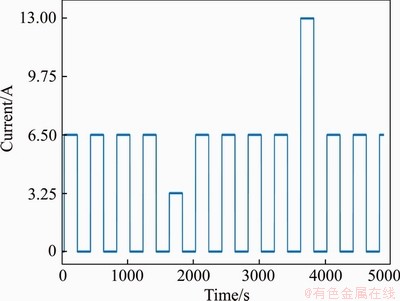
Figure 7 Waveform of discharge current set to 50% and 200% of normal value in two discharge cycles
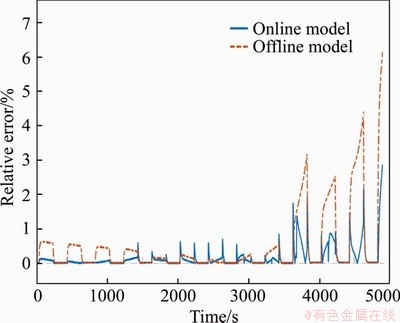
Figure 8 Errors of dynamic responses of online model and offline model
Contributors
LI Gang provided the concept and analyzed the model of battery. JI Yan-ju conducted the literature review and wrote the first draft of the manuscript. QIU Shi-lin finished the simulation, analyzed the results and edited the draft of manuscript.
Conflict of interest
JI Yan-ju, QIU Shi-lin and LI Gang declare that they have no conflict of interest.
References
[1] FRIESKE B, KLOETZKE M, MAUSER F. Trends in vehicle concept and key technology development for hybrid and battery electric vehicles [J]. World Electric Vehicle Journal, 2013, 6(1): 9-20. DOI: 10.3390/wevj6010009.
[2] DRAGOMIR F, DRAGOMIR O E, OPREA A, OLTEANU L, OLARIU N, URSU V. Simulation of lithium-ion batteries from a electric vehicle perspective [C]// 2017 Electric Vehicles International Conference. 2017: 1-5. DOI: 10.1109/ EV.2017. 8242100.
[3] GIORDANO G, KLASS V, BEHM M, LINDBERGH G, SJOBERG J. Model-based lithium-ion battery resistance estimation from electric vehicle operating data [J]. IEEE Transactions on Vehicular Technology, 2018, 67(5): 3720-3728. DOI: 10.1109/TVT.2018.2796723.
[4] FENG Fei, SONG Kai, LU Ren-gui, WEI Guo, ZHU Chun-bo. Equalization control strategy and SOC estimation for LiFePO4 battery pack [J]. Transactions of China Electrotechnical Society, 2015, 30(1): 22-29. DOI: 10.19595/j.cnki.1000-6753.tces.2015.01.004. (in Chinese)
[5] LYU C, LAI Q, WANG R, SONG Y, LIU H, ZHANG L, LI F. A research of thermal coupling model for lithium-ion battery under low-temperature conditions [C]// 2017 Prognostics and System Health Management Conference. 2017: 1-5. DOI: 10.1109/PHM.2017.8079131.
[6] YANG Ju-feng, XIA Bing, SHANG Yun-long, HUANG Wen-xin, MI C C. Adaptive state-of-charge estimation based on a split battery model for electric vehicle applications [J]. IEEE Transactions on Vehicular Technology, 2017, 66(12): 10889-10898. DOI: 10.1109/TVT.2017.2728806.
[7] EINHORN M, CONTE FV, KRAL C, FLEIG J. Comparison, selection, and parameterization of electrical battery models for automotive applications [J]. IEEE Transactions on Power Electronics, 2013, 28(3): 1429-1437. DOI: 10.1109/ TPEL.2012.2210564.
[8] LIU Si-jia, JIANG Jiu-chun, SHI Wei, MA Ze-yu, WANG Le-yi, GUO Hong-yu. Butler-volmer-equation-based electrical model for high-power lithium titanate batteries used in electric vehicles [J]. IEEE Transactions on Industrial Electronics, 2015, 62(12): 7557-7568. DOI: 10.1109/TIE. 2015.2449776.
[9] SEAMAN A, DAO T, MCPHEE J. A survey of mathematics-based equivalent-circuit and electrochemical battery models for hybrid and electric vehicle simulation [J]. Journal of Power Sources, 2014, 256: 410-423. DOI: 10.1016/j.jpowsour.2014.01.057.
[10] LI Si, CHENG Xi-ming. A comparative study on RC models of lithium-ion battery [C]// 2014 IEEE Conference and Expo Transportation Electrification Asia-Pacific. 2014: 1-4. DOI: 10.1109/ITEC-AP.2014.6940818.
[11] HU Xiao-song, SUN Feng-chun, ZOU Yuan. Online model identification of lithium-ion battery for electric vehicles [J]. Journal of Central South University of Technology, 2011, 18(5): 1525-1531. DOI: 10.1007/s11771-011-0869-1.
[12] POP O, TAUT A, GRAMA A, FIZESAN R, CEUCA E. PSpice discharge model for simulation circuits with lead-acid battery [C]// 2017 40th International Spring Seminar on Electronics Technology. 2017: 1-4. DOI: 10.1109/ISSE.2017. 8000943.
[13] LAI Xin, ZHENG Yue-jiu, SUN Tao. A comparative study of different equivalent circuit models for estimating state-of- charge of lithium-ion batteries [J]. Electrochimica Acta, 2018, 259: 566-577. DOI: 10.1016/j.electacta.2017.10.153.
[14] HU Ming-hui, LI Yun-xiao, LI Shu-xian, FU Chun-yun, QIN Da-tong, LI Zong-hua. Lithium-ion battery modeling and parameter identification based on fractional theory [J]. Energy, 2018, 165: 153-163. DOI: 10.1016/j.energy.2018. 09.101.
[15] YOU H W, BAE J I, CHO S J, LEE J M, KIM S. Analysis of equivalent circuit models in lithium-ion batteries [J]. AIP Advances, 2018, 8(12): 125101. DOI: 10.1063/1.5054384.
[16] SU Jie, LIN Mao-song, WANG Shun-li, LI Jin, COFFIE- KEN J, XIE Fei. An equivalent circuit model analysis for the lithium-ion battery pack in pure electric vehicles [J]. Measurement and Control, 2019, 52(3, 4): 193-201. DOI: 10.1177/0020294019827338.
[17] BAO Qiang, CHENG Yan, WU Zhong-jian. The dynamic impedance modeling and simulation analysis of lithium battery cell in micro power grid [C]// 2017 12th IEEE Conference on Industrial Electronics and Applications. 2017: 1613-1618. DOI: 10.1109/ICIEA.2017.8283097.
[18] LUO Qing-zhu, AN Ai-min, ZHANG Hao-chen, MENG Fan-cheng. Non-linear performance analysis and voltage control of MFC based on feedforward fuzzy logic PID strategy [J]. Journal of Central South University, 2019, 26(12): 3359-3371. DOI: 10.1007/s11771-019-4259-4.
[19] LIU Fang, MA Jie, SU Wei-xing, CHEN Han-ning, TIAN Hui-xin, LI Chun-qing. SOC estimation based on data driven extended Kalman filter algorithm for power battery of electric vehicle and plug-in electric vehicle [J]. Journal of Central South University, 2019, 26(6): 1402-1415. DOI: 10.1007/s11771-019-4096-5.
[20] CHARKHGARD M, FARROKHI M. State-of-charge estimation for lithium-ion batteries using neural networks and EKF [J]. IEEE Transactions on Industrial Electronics, 2010, 57(12): 4178-4187. DOI: 10.1109/TIE.2010.2043035.
[21] RAHIMI-EICHI H, BARONTI F, CHOW M. Online adaptive parameter identification and state-of-charge coestimation for lithium-polymer battery cells [J]. IEEE Transactions on Industrial Electronics, 2014, 61(4): 2053-2061. DOI: 10.1109/TIE.2013.2263774.
[22] ZHU Qiao, LI Liang, HU Xiao-song, XIONG Neng, HU Guang-di. H∞-based nonlinear observer design for state of charge estimation of lithium-ion battery with polynomial parameters [J]. IEEE Transactions on Vehicular Technology, 2017, 66(12): 10853-10865. DOI: 10.1109/TVT.2017. 2723522.
[23] LIU Xiang-yong, LI Wan-li, ZHOU Ai-guo. PNGV equivalent circuit model and SOC estimation algorithm for lithium battery pack adopted in AGV vehicle [J]. IEEE Access, 2018, 6: 23639-23647. DOI: 10.1109/ACCESS. 2018.2812421.
[24] Battery documentation [M]. MathWorks Inc, 2020. https:// ww2.mathworks.cn/help/physmod/sps/powersys/ref/battery.html?searchHighlight=Battery&s_tid=doc_srchtitle.
[25] HURIA T, CERAOLO M, GAZZARRI J, JACKEY R. High fidelity electrical model with thermal dependence for characterization and simulation of high power lithium battery cells [C]// 2012 IEEE International Electric Vehicle Conference. 2012: 1-8. DOI: 10.1109/IEVC.2012.6183271.
[26] Curve fitting toolbox documentation [M]. MathWorks Inc, 2020. https://ww2.mathworks.cn/help/curvefit/index.html?s_ tid=srchtitle.
(Edited by FANG Jing-hua)
中文导读
基于可变电阻和电容的锂电池二阶RC等效电路模型的仿真
摘要:随着电动汽车产业的兴起,作为电动汽车的动力源的锂电池已成为研究热点。本文研究了锂电池的荷电状态(SOC)估算和建模。分析基于外部特性的安时(Ah)积分方法和研究开路电压(OCV)方法,并将这两种方法结合起来估算SOC。考虑到模型的准确性和复杂性,选择了锂电池的二阶RC等效电路模型。对锂电池进行脉冲放电和指数拟合得到相应的参数,通过分别使用固定电阻电容和可变电阻电容器进行模拟。可变电阻和电容模型的精度为2.9%,验证了本文所提出模型的有效性。
关键词:锂电池;等效电路模型;参数识别;SOC估算
Foundation item: Project(51507073) supported by the National Natural Science Foundation of China
Received date: 2020-01-28; Accepted date: 2020-06-23
Corresponding author: LI Gang, PhD, Associate Professor; Tel: +86-18186883264, E-mail: ligang2013@jlu.edu.cn; ORCID: https:// orcid.org/ 0000-0002-2648-0538