考虑衬砌屈服的深埋水工隧洞应力解析解
曾开华,黎剑华,许家雄,叶青
(南昌工程学院 土木与建筑工程学院, 江西 南昌,330099)
摘要:采用统一强度理论,根据不同工况下不同的应力状态,正确选择第1主应力,推导考虑衬砌屈服的深埋水工隧洞应力解析解。当选取不同的统一强度理论参数b时,可得到一系列有序的应力场公式、临界压力公式和塑性区半径与内水压力的关系,能适用于更多的材料和结构。通过工程算例,比较本文方法与传统方法的不同,说明考虑第1主应力的变化是正确的,更符合工程实际,并得出统一强度理论参数对衬砌和围岩应力的影响特性,最后根据临界压力给出了公式的适用条件。该结果为水工隧洞的弹塑性应力分析提供理论依据,对工程设计有一定的参考价值。
关键词:圆形隧洞;衬砌;统一强度理论;弹塑性分析
中图分类号:TU457 文献标志码:A 文章编号:1672-7207(2012)03-1131-07
Analytical solution for stresses of deep hydraulic tunnel considering linear yielding
ZENG Kai-hua, LI Jian-hua, XU Jia-xiong, YE Qing
(Department of Civil Engineering, Nanchang Institute of Technology, Nanchang 330099, China)
Abstract: With proper choice of the first principal stress according to different stress states in different engineering instances, an analytical solution for stresses around a deep hydraulic tunnel with liner yielding was deduced based on the unified strength theory. Choosing different unified strength theory parameter (b), a series of orderly stress field, critical pressure and the plastic radius versus the inner hydraulic pressure were obtained, which can be adopted for more materials and structures. The differences were found between this paper’s method and the traditional method through an engineering case. The results show that it is accurate and more accord with engineering practice to consider the difference of first principal stress. The influence of the unified strength theory parameter is discussed. The applicability of the obtained formulas is gained according to the critical pressures.
Key words: circular tunnel; liner; unified strength theory; elastic-plastic analysis
水工压力隧洞断面常采用圆形,并设置衬砌。洞室开挖使隧洞周围岩体应力产生重分布,以往对压力隧洞的弹塑性分析,多采用Mohr-Coulomb(M-C)或Hoek-Brown(H-B)强度准则[1-6]。M-C和H-B强度准则由于没有考虑中间主应力σ2的影响而偏于保守,大量的岩石真三轴试验结果证实[7],中间主应力σ2可使岩石强度提高30%左右;其次,正如Tresca和Mises强度准则分别仅适用τs=σs和τs=0.577σs的材料一样,M-C强度准则仅适用于τs=σtσc/(σt+σc)的材料,其中σt,σc,σs和τs分别为材料的抗拉强度、抗压强度、屈服强度和抗剪强度。统一强度理论[8-10]合理地反映了中间主应力效应及其区间性,可以灵活地适用于工程上的各类材料,在隧洞弹塑性分析中已获得广泛的应 用[11-15]。现有各种结果大都是针对无支护隧洞或将支护用一个支护力代替,并且应用M-C强度准则时,常以径向应力作为第1主应力。实际上,由于隧洞在不同的工况下,第1主应力可能是径向应力,也可能是环向应力,在应用强度准则时应正确选择第1主应力。任青文等[3]和宋俐等[11]已经考虑到这一点,修正了Fenner公式,但均未考虑衬砌作用,且文献[11]仅根据内水压力是否大于初始地应力来确定第1主应力,在理论上不完全正确。任青文等[4]虽考虑了衬砌作用,但没有考虑中间主应力σ2的影响,所得结果偏保守。张常辉等[14-15]考虑了中间主应力σ2的影响,但假设衬砌为理想弹性材料,不太符合实际情况。因为衬砌需要与围岩共同作用,同时为了使围岩分担更多的荷载,衬砌往往首先进入塑性状态,故隧洞的应力大小和分布应考虑衬砌所处的不同屈服状态。本文作者针对具有衬砌的深埋水工隧洞,采用统一强度理论,根据不同的工况,正确选择第1主应力,考虑衬砌不同的屈服状态,推导了衬砌和围岩弹塑性应力解析解,给出了第1临界压力和第2临界压力的计算公式,并通过算例分析塑性区范围随内水压力变化的规律以及本文方法与传统方法的不同,得到统一强度理论参数对隧洞应力的影响特性,最后根据临界压力给出了公式的适用条件。文献[4]是本文的一个特例。
1 统一强度理论
1991年西安交通大学的俞茂宏教授采用双剪应力的概念,建立了一种全新的考虑中间主应力σ2影 响,能适用于各类材料的统一强度理论。其数学表达式为[8-10]:
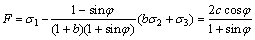
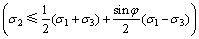 (1a)
(1a)
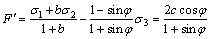
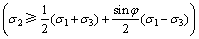 (1b)
(1b)
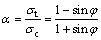 ,
,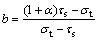
式中:σ1和σ3分别为第1主应力和第3主应力,拉应力为正,压应力为负,按应力代数值代入,σ1≥σ2≥σ3;c和φ?分别为黏聚力和内摩擦角;α为材料拉压比;b为反映中间主剪应力及其面上的正应力对材料屈服或破坏影响程度的参数,称为统一强度理论参数,0≤b≤1,同时b也是选择不同强度准则的参数。
2 第1主应力为径向应力
设深埋圆形隧洞内半径为r1,衬砌外半径为r2,均匀内水压力为p,初始地应力为po,塑性区外半径为rp,如图1所示。衬砌在开挖后立即施作,不考虑围岩初始地应力的部分释放。为了使围岩分担更多的荷载,发挥其结构自承载能力,衬砌一般首先进入塑性状态[4]。设衬砌和围岩均是理想弹塑性材料,衬砌的弹性模量和泊松比分别为E1和μ1,抗剪强度参数为c1和φ1;围岩的弹性模量和泊松比分别为E2和μ2,抗剪强度参数为c2和φ2。
在施工期,隧洞开挖使围岩应力重分布,或运行期内水压力较小时,衬砌和(或)临近的围岩就会进入塑性状态,此时第1主应力多为径向应力(本文取拉应力为正),可分为弹塑性界面位于衬砌内和围岩内2种情况。
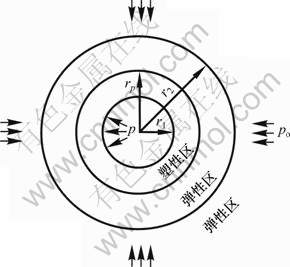
图1 弹塑性界面位于衬砌内
Fig.1 Interface of elastic and plastic regions in liner
2.1 弹塑性界面位于衬砌内(r1≤rp≤r2)
此时衬砌处于弹塑性状态,有塑性区和弹性区;围岩全部处于弹性状态。对r1≤r≤rp的衬砌塑性区 (见图1)。以极坐标表示的应力平衡微分方程为:
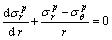 (2)
(2)
深埋隧洞处于平面应变状态,纵向应力σz为中间主应力,在塑性区内[10]:
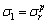 ,
,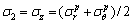 ,
,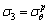 (3)
(3)
满足式(1(a)),并利用边界条件
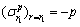 (4)
(4)
且在衬砌内有c=c1,φ=φ1,求得:
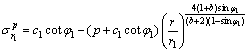 (5a)
(5a)
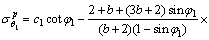
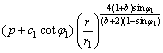 (5b)
(5b)
对r≥rp的衬砌弹性区和围岩弹性区,见图1,其弹性应力分别为[4, 16]:
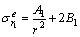 ,
,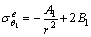 (6)
(6)
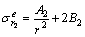 ,
,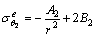 (7)
(7)
式中: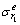 ,
,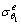 ,
,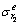 和
和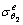 分别为衬砌和围岩弹性区
分别为衬砌和围岩弹性区
的径向应力和环向应力;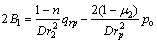 ;
;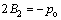 ;
;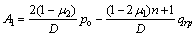 ;
;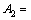
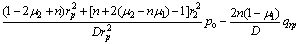 ;
;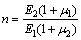 ;
;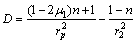 。
。
由衬砌弹性区内边界r=r1处的应力满足屈服条件,可求出由于围岩应力重分布或内水压力较小,使衬砌开始屈服时的弹性极限压力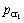 ,称
,称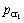 为第1临界压力,其表达式为:
为第1临界压力,其表达式为:
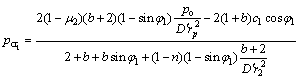 (8)
(8)
式中: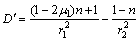 。
。
根据衬砌弹塑性交界r=rp处的径向应力连续,以及径向应力和环向应力之和不变,可求得弹塑性交界处的接触压力qrp和塑性区半径rp的隐式计算式分 别为:
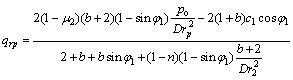 (9)
(9)
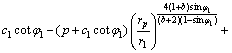
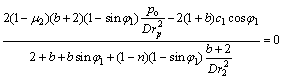 (10)
(10)
式(10)是关于rp的超越方程,可采用迭代方法求解。由式(10)求出rp,代入式(9)得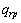 ,按式(6)和式(7)计算弹性区应力,塑性区应力由式(5)确定。
,按式(6)和式(7)计算弹性区应力,塑性区应力由式(5)确定。
2.2 弹塑性界面位于围岩内(rp≥r2)
此时围岩处于弹塑性状态,有塑性区和弹性区;衬砌处于完全塑性状态。对于r1≤r≤rp的衬砌塑性区和围岩塑性区,如图2所示。
利用边界条件
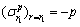 ,
,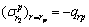
可求得衬砌塑性区与围岩塑性区的应力分别为
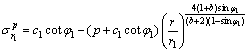
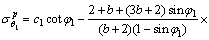
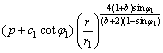
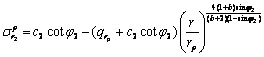
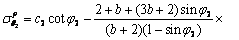
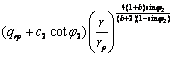 (11)
(11)
围岩弹性区的应力为:
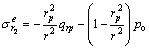
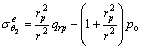 (12)
(12)
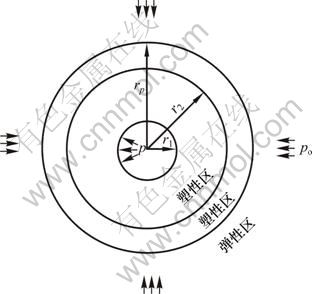
图2 弹塑性界面位于围岩内
Fig.2 Interface of elastic and plastic regions in rock
弹塑性交界处的接触压力qrp为:
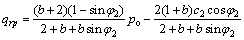 (13)
(13)
关于塑性区半径rp的隐式计算式为:
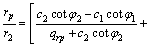
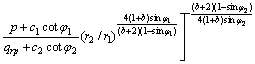 (14)
(14)
由式(13)求出qrp,代入式(14)得rp,按式(11)和式(12)分别计算隧洞塑性区和弹性区应力。
由式(14)可得出弹塑性界面位于围岩内所满足的条件,即rp≥r2成立的条件,整理得:
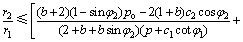
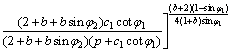 (15)
(15)
可见,衬砌厚度较小且内水压力p较大时,式(15)越易成立,隧洞塑性区才更易从衬砌扩展到围岩内。
3 第1主应力为环向应力
对于深埋水工压力隧洞,运行期洞壁内水压力多为控制荷载,衬砌和(或)围岩也可能出现塑性区。但应用统一强度理论时,由于径向压应力较大,环向压应力较小,甚至成为拉应力,所以此时第1主应力应为环向应力。
3.1 弹塑性界面位于衬砌内(r1≤rp≤r2)
衬砌塑性区的应力为:
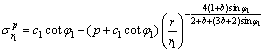
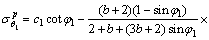
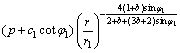 (16)
(16)
对r≥rp的弹性区,衬砌和围岩应力仍按式(6)和式(7)计算。
衬砌弹塑性交界处的径向接触压力qrp为:
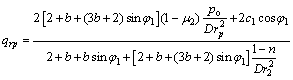 (17)
(17)
由于内水压力太大,使衬砌再次发生屈服时的弹性极限压力为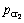 ,称
,称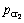 为第2临界压力。
为第2临界压力。
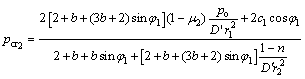 (18)
(18)
关于塑性区半径rp的隐式计算式为:
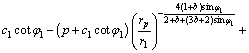
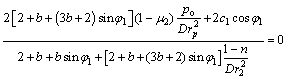 (19)
(19)
由式(19)求出rp,代入式(18)得qrp,按式(6)和式(7)计算衬砌和围岩弹性区应力,衬砌塑性区应力由式(16)确定。
3.2 弹塑性界面位于围岩内(rp≥r2)
衬砌塑性区和围岩塑性区的应力分别为:
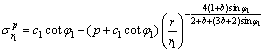
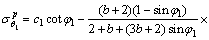
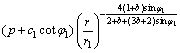
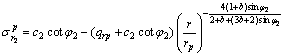
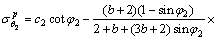
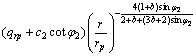 (20)
(20)
对于r≥rp的围岩弹性区,应力仍按式(12)计算。
关于塑性区半径rp的隐式计算式为:
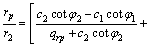
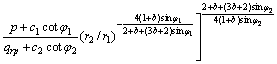 (21)
(21)
围岩弹塑性交界处的径向接触压力qrp为:
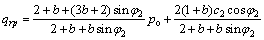 (22)
(22)
由式(22)求出qrp,代入式(21)得rp,按式(20)和式(12)分别计算隧洞塑性区和弹性区应力。
弹塑性界面位于围岩内,即rp≥r2的条件为:
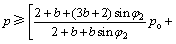
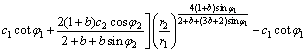 (23)
(23)
此时,才能使塑性区范围扩展到围岩内。
上述隧洞应力解析解分为衬砌部分屈服和完全屈服两种情况,均考虑了中间主应力σ2效应和第1主应力的正确选择。当选取不同的参数b时,可以得到一系列有序的应力场公式、临界压力公式和塑性区半径与内水压力的关系,能适用于更多的材料和结构。
4 算例和公式的适用条件
4.1 算例
具有衬砌的深埋圆形水工压力隧洞[4],隧洞内半径r1=4 m,衬砌外半径r2=5 m,初始地应力po=10 MPa。衬砌材料参数E1=20 GPa,μ1=0.167,c1=5 MPa,φ1=45o。围岩材料参数E2=2 GPa,μ2=0.25,c2=1 MPa,φ2=45o。
通过统一强度理论参数b的变化来分析中间主应力σ2效应和不同强度准则的影响,b=0时,统一强度理论退化为M-C强度准则;b=1时,退化为双剪应力强度理论。当b=0.6时,隧洞开挖时内水压力p=0,由式(10)求得塑性区半径rp为4.49 m,弹塑性界面位于衬砌内,由式(9)求得弹塑性交界处的径向接触压力qrp为5.08 MPa。在隧洞运行期,随着p的增加,塑性区范围逐渐减少。当p增大到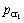 =3.15 MPa时,由式(10)求得rp=4 m,塑性区消失。当p在
=3.15 MPa时,由式(10)求得rp=4 m,塑性区消失。当p在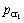 =3.15 MPa和
=3.15 MPa和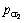 = 18.3 MPa之间时,衬砌和围岩始终都处于弹性状态。当p=18.3 MPa时,由式(18)求得rp=4 m,衬砌又开始出现塑性区,这是由于p过大引起的。当rp=5 m时,由式(21)求得内水压力p1=19.67 MPa,但由式(23)求得内水压力p2=23.12 MPa,才能使塑性区范围扩展到围岩内,所以,p在p1~p2之间时,rp一直为5 m。当p超过23.12 MPa并继续增大时,塑性区范围在围岩内进一步扩大。当b取其他值时,如表1所示。
= 18.3 MPa之间时,衬砌和围岩始终都处于弹性状态。当p=18.3 MPa时,由式(18)求得rp=4 m,衬砌又开始出现塑性区,这是由于p过大引起的。当rp=5 m时,由式(21)求得内水压力p1=19.67 MPa,但由式(23)求得内水压力p2=23.12 MPa,才能使塑性区范围扩展到围岩内,所以,p在p1~p2之间时,rp一直为5 m。当p超过23.12 MPa并继续增大时,塑性区范围在围岩内进一步扩大。当b取其他值时,如表1所示。
表1 不同b值所对应的rp, qrp, 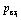 ,
,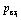 , p1和p2
, p1和p2
Table 1 rp, qrp, 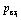 ,
,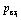 , p1 and p2 with different b
, p1 and p2 with different b
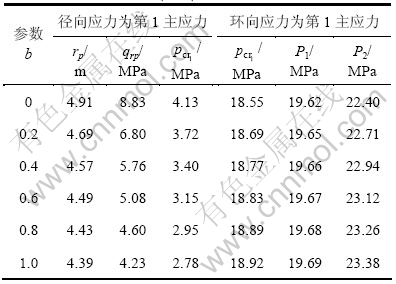
从表1可知:随着参数b的增大,rp,qrp和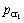 在减小,而
在减小,而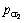 和p2在增大,这都说明考虑中间主应力σ2的影响,可以更好地发挥岩石类材料的强度潜能,更客观地认识其自承载能力。
和p2在增大,这都说明考虑中间主应力σ2的影响,可以更好地发挥岩石类材料的强度潜能,更客观地认识其自承载能力。
图3给出b=0和b=1时,分别按第1主应力始终为径向应力和本文方法计算所得的塑性区外半径rp和内水压力p的关系。方法1代表第1主应力始终为径向应力,方法2代表本文方法。
从图3可知:随着p的增大,2种方法在p<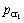 时,计算结果相同。当p>
时,计算结果相同。当p>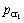 时,如果不考虑第一主应力的变化,即始终将径向应力σr作为第一主应力,也就是说,当p>
时,如果不考虑第一主应力的变化,即始终将径向应力σr作为第一主应力,也就是说,当p>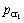 ,甚至p>
,甚至p>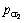 时,仍然按式(10)或式(14)计算塑性区外半径rp,就会出现rp<r1,而且p越大,rp就越小,衬砌和围岩都处于完全弹性状态,隧洞安全等级高,这与实际情况矛盾。考虑到不同工况下,衬砌和(或)围岩进入塑性状态的原因不同,应分别按不同第一主应力情况下的公式计算塑性区范 围[3-4, 11, 14-15]。方法2考虑了不同工况下主应力顺序,计算结果更符合工程实际。在p相同时,b=1时的rp总小于b=0时的rp,且随着p的增大,二者差异越大。
时,仍然按式(10)或式(14)计算塑性区外半径rp,就会出现rp<r1,而且p越大,rp就越小,衬砌和围岩都处于完全弹性状态,隧洞安全等级高,这与实际情况矛盾。考虑到不同工况下,衬砌和(或)围岩进入塑性状态的原因不同,应分别按不同第一主应力情况下的公式计算塑性区范 围[3-4, 11, 14-15]。方法2考虑了不同工况下主应力顺序,计算结果更符合工程实际。在p相同时,b=1时的rp总小于b=0时的rp,且随着p的增大,二者差异越大。
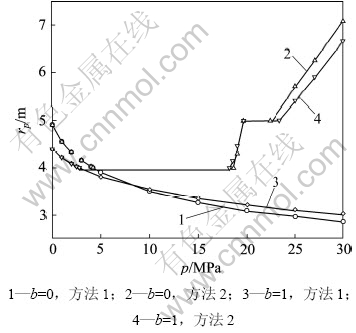
图3 塑性区半径rp与内水压力p的关系
Fig.3 Relations of plastic radius and inner hydraulic pressure
图4给出当b=1,p=25 MPa时,衬砌和围岩的应力分布。由于p>p2,由式(21)求得rp=5.40 m,此时弹塑性界面位于围岩内,因此,应按式(20)和式(12)分别计算隧洞塑性区和弹性区应力。而按方法1,由式(10)求得rp=3.12 m,衬砌和围岩都处于完全弹性状态。
从图4可以看出,对于运行期内水压力较高,隧洞的弹塑性界面将位于围岩内,此时方法1计算得到的应力分布与本文方法所得结果的差异显著。在弹塑性交界处,由于衬砌与围岩的材料参数不同,且只能保证其径向应力连续,环向应力在此处有跌落,本文方法所得跌落值相对较小,更符合实际工程情况。
4.2 公式适用条件
实际应用时,应根据岩石力学试验和工程实际情况,合理地确定参数b;根据临界压力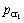 和(或)
和(或) 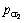 ,选择相应的公式确定塑性区范围和应力计算公式。
,选择相应的公式确定塑性区范围和应力计算公式。
当p<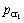 时(一般为施工期或内水压力较小时的运行期),径向应力为第1主应力,衬砌和(或)部分围岩由于初始地应力重分布或内水压力太小进入塑性状态,应按本文有关公式确定塑性区范围、塑性区和弹性区的应力分布。
时(一般为施工期或内水压力较小时的运行期),径向应力为第1主应力,衬砌和(或)部分围岩由于初始地应力重分布或内水压力太小进入塑性状态,应按本文有关公式确定塑性区范围、塑性区和弹性区的应力分布。
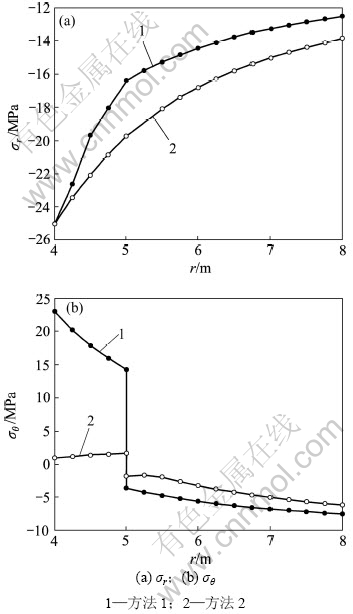
图4 b=1,p=25 MPa时不同半径处的应力分布
Fig.4 Distributions of stress at different radius when b=1, p=25 MPa
当p>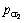 时(一般为运行期),环向应力为第1主应力,衬砌和(或)部分围岩由于内水压力太大进入塑性状态,应按本文有关公式确定塑性区范围、塑性区和弹性区的应力分布。
时(一般为运行期),环向应力为第1主应力,衬砌和(或)部分围岩由于内水压力太大进入塑性状态,应按本文有关公式确定塑性区范围、塑性区和弹性区的应力分布。
当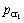 ≤p≤
≤p≤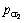 时,衬砌和围岩都处于完全弹性状态,可按弹性力学有关公式计算[16]。
时,衬砌和围岩都处于完全弹性状态,可按弹性力学有关公式计算[16]。
5 结论
(1) 针对具有衬砌的深埋圆形水工隧洞,采用统一强度理论,考虑不同工况下主应力顺序和衬砌的屈服状态,推导了衬砌和围岩的弹塑性应力解析解,文献[4]是本文统一强度理论参数b=0时的一个特例。
(2) 选取不同的统一强度理论参数b,可以得到一系列有序的应力场公式、临界压力公式和塑性区半径与内水压力的关系,能适用于更多的材料和结构。
(3) 式(8)和(18)分别给出了第1临界压力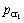 和第2临界压力
和第2临界压力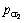 的计算公式。随着参数b的增大,
的计算公式。随着参数b的增大,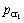 在减小,
在减小,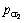 在增大,这都说明考虑中间主应力σ2可以更好地发挥岩石类材料的强度潜能,更客观地认识其自承载能力。
在增大,这都说明考虑中间主应力σ2可以更好地发挥岩石类材料的强度潜能,更客观地认识其自承载能力。
(4) 通过算例分析了塑性区半径rp随内水压力p和参数b的变化情况。如果不考虑第1主应力的变化,就会出现当p>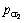 时,衬砌和围岩都处于完全弹性状态,与实际情况矛盾,这说明考虑第1主应力的变化是正确的,更符合工程实际。
时,衬砌和围岩都处于完全弹性状态,与实际情况矛盾,这说明考虑第1主应力的变化是正确的,更符合工程实际。
(5) 实际应用时,应根据岩石力学试验和实际工程情况,合理地选取参数b,最后根据临界压力给出了公式的适用条件。
参考文献:
[1] Jaeger J C, Cook N G W. Fundamentals of rock mechanics[M]. London: Chapman and Hall, 1979: 252-280.
[2] Jiang Y, Yoneda H, Tanabashi Y, et al. Theoretical estimation of loosening pressure on tunnels in soft rocks[J]. Tunneling and Underground Space Technology, 2001, 16(2): 99-105
[3] 任青文, 张宏朝. 关于芬纳公式的修正[J]. 河海大学学报, 2001, 29(16): 109-111.
REN Qing-wen, ZHANG Hong-chao. A modification of Fanner formula[J]. Journal of Hohai University, 2001, 29(16): 109-111.
[4] 任青文, 邱颖. 具有衬砌圆形隧洞的弹塑性解[J]. 工程力学, 2005, 22(2): 212-217.
REN Qing-wen, QIU Ying. Elastic-plastic solution of circular tunnel with liner[J]. Engineering Mechanics, 2005, 22(2): 212-217.
[5] Wang Y. Ground response of circular tunnel in poorly consolidated rock[J]. Journal of Geotechnical Engineering, ASCE, 1996, 122(9): 703-708.
[6] Sharan S K. Analytical solutions for stresses and displacements around a circular opening in a generalized Hoek-Brown rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45(1): 78-85.
[7] 许东俊, 耿乃光. 岩石强度随中间主应力变化规律[J]. 固体力学学报, 1985, 6(1): 72-80.
XU Dong-jun, GENG Nai-guang. The variation law of rock strength with increase of intermediate principal stress[J]. Acta Mechanica Solida Sinica, 1985, 6(1): 72-80.
[8] 俞茂宏. 双剪理论及其应用[M]. 北京: 高等教育出版社, 1998: 249-287.
YU Mao-hong. Twin-shear theory and its application[M]. Beijing: Science Press, 1998: 249-287.
[9] 俞茂宏. 岩土类材料的统一强度理论及其应用[J]. 岩土工程学报, 1994, 16(2): 1-10.
YU Mao-hong. Unified strength theory for geomaterials and its applications[J]. Chinese Journal of Geotechnical Engineering, 1994, 16(2): 1-10.
[10] 俞茂宏, 杨松岩, 刘春阳, 等. 统一平面应变滑移线场理论[J]. 土木工程学报, 1997, 30(2): 14-26.
YU Mao-hong, YANG Song-yan, LIU Chun-yang, et al. Unified plane-strain slip line field theory system[J]. China Civil Engineering Journal, 1997, 30(2): 14-26.
[11] 宋俐, 张永强, 俞茂宏. 压力隧洞弹塑性分析的统一解[J]. 工程力学, 1998, 15(4): 57-61.
SONG Li, ZHANG Yong-qiang, YU Mao-hong. Elastic-plastic unified analysis of pressure tunnel[J]. Engineering Mechanics, 1998, 15(4): 57-61.
[12] 胡小荣, 俞茂宏. 统一强度理论及其在巷道围岩弹塑性分析中的应用[J]. 中国有色金属学报, 2002, 12(5): 1021-1026.
HU Xiao-rong, YU Mao-hong. Unified strength theory and its application in elasto-plastic analysis to tunnel[J]. The Chinese Journal of Nonferrous Metals, 2002, 12(5): 1021-1026.
[13] 陈立伟, 彭建兵, 范文, 等. 基于统一强度理论的非均匀应力场圆形巷道围岩塑性区分析[J]. 煤炭学报, 2007, 23(1): 20-23.
CHEN Li-wei, PENG Jian-bin, FAN Wen, et al. Analysis of surrounding rock mass plastic zone of round tunnel under non-uniform stress field based on the unified strength theory[J]. Journal of China Coal Society, 2007, 23(1): 20-23.
[14] 张常光, 张庆贺, 赵均海, 等. 具有衬砌的圆形水工隧洞弹塑性应力统一解[J]. 同济大学学报: 自然科学版, 2010, 38(1): 50-53, 134.
ZHANG Chang-guang, ZHANG Qing-he, ZHAO Jun-hai, et al. Elastic-plastic stress unified solutions of a circular hydraulic with lining[J]. Journal of Tongji University: Natural Science, 2010, 38(1): 50-53, 134.
[15] 张常光, 胡云世, 赵均海, 等. 深埋圆形水工隧洞弹塑性应力和位移统一解[J]. 岩土工程学报, 2010, 32(11): 1738-1745.
ZHANG Chang-guang, HU Yun-shi, ZHAO Jun-hai, et al. Elastic-plastic unified solutions for stresses and displacements of a deep buried circular tunnel[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(11): 1738-1745.
[16] 徐芝纶. 弹性力学[M]. 北京: 人民教育出版社, 1982: 73-108.
XU Zhi-lun. Elasticity[M]. Beijing: Pople’s Education Press, 1982: 73-108.
(编辑 陈爱华)
收稿日期:2010-04-04;修回日期:2011-06-06
基金项目:国家自然科学基金资助项目(50969007)
通信作者:曾开华(1968-),男,江西丰城人,副教授,从事地下工程设计与施工、地基处理和边坡加固等研究;电话:15079109180;E-mail: nczkh1968@163.com