Effect of material parameters on stress wave propagation during fast upsetting

WANG Zhong-jin(王忠金), CHENG Li-dong(程利冬)

School of Materials Science and Engineering, Harbin Institute of Technology, Harbin 150001, China

Received 23 December 2007; accepted 13 June 2008

Abstract: Based on a dynamic analysis method and an explicit algorithm, a dynamic explicit finite element code was developed for modeling the fast upsetting process of block under drop hammer impact, in which the hammer velocity during the deformation was calculated by energy conservation law according to the operating principle of hammer equipment. The stress wave propagation and its effect on the deformation were analyzed by the stress and strain distributions. Industrial pure lead, oxygen-free high-conductivity (OFHC) copper and 7039 aluminum alloy were chosen to investigate the effect of material parameters on the stress wave propagation. The results show that the stress wave propagates from top to bottom of block, and then reflects back when it reaches the bottom surface. After that, stress wave propagates and reflects repeatedly between the upper surface and bottom surface. The stress wave propagation has a significant effect on the deformation at the initial stage, and then becomes weak at the middle-final stage. When the ratio of elastic modulus or the slope of stress—strain curve to mass density becomes larger, the velocity of stress wave propagation increases, and the influence of stress wave on the deformation becomes small.

Key words: fast upsetting; stress wave; material parameter; dynamic explicit; finite element

1 Introduction

Fast upsetting under drop hammer impact is a primary method to investigate the deformation behavior of metal under medium strain rate. During the fast upsetting process, the workpiece is subjected to dynamic impact loading. A significant inertial force occurs in the workpiece, and the stress wave propagation has an important effect on the deformation, which makes the analysis of fast upsetting process become more complex than that of quasi-static upsetting[1-4].

Stress wave is a kind of perturbed propagation for stress (or strain), and stress wave propagation can depict deformation process of material under dynamic loading. Stress wave propagation is closely related to the material parameters, and the material parameters have a significant effect on the propagation process of stress wave. The previous theory and experimental work show that there are two kinds of stress waves with different propagating velocities in an elastoplastic material. The quicker one is elastic wave with lower stress peak value, and the slower one is plastic wave with higher stress peak value[5-8].

There are three common methods to investigate the problem of stress wave propagation, that is, characteristic line method, finite difference method and finite element method[9-11]. For the dynamic deformation of metal, the dynamic explicit finite element method is proper to be adopted and mainly used in one or two dimensional problems due to the complexity of three dimensional problems[12]. ARGYRIS and CHAN[13] did research on the fast upsetting process of cylinder using a two-dimensional dynamic explicit finite element code, and revealed that the stress wave propagation could perturb the relationship curve between the acceleration and deformation time. Current available commercial finite element softwares for hammer forging adopt static implicit algorithm, such as Deform, Superform and Qform, in which hammer forging is treated as a quasi-static process, and the effect of stress wave on the deformation cannot be considered.

In order to analyze the stress wave propagation in the fast upsetting process under drop hammer impact, based on the dynamic explicit algorithm and elastoplastic finite deformation theory, a three-dimensional finite element code was developed, in which the hammer velocity was calculated by the energy conservation law. The block upsetting processes were simulated using the developed code. The stress and strain distributions were calculated to investigate the stress wave propagation and its influence on the deformation. Industrial pure lead, OFHC (oxygen-free high- conductivity) copper and 7039 aluminum alloy were chosen to analyze the effect of material parameters on the stress wave propagation.

2.1 Dynamic explicit algorithm

For an elastoplastic solid, the equation governing the motion can be expressed as

where  M is the consistent mass matrix, ü is the acceleration vector, P and F are the vectors of external and internal nodal force, respectively, H is the added Hourglass resisting force to prevent Hourglass mode in the calculation. There are two methods to calculate Hourglass force: stiff Hourglass control and viscous Hourglass control[14]. In the developed code, the latter is proper to be used.

The central difference scheme was used to integrate Eqn.(1). The acceleration ü, velocity 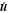 and displacement u are expressed as[15]

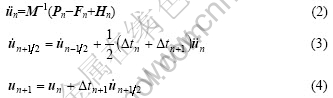
The central difference scheme is conditionally stable. At each time incremental step, a time increment is required to less than a critical value:

where   the range of stable factor ξ is 0.5-0.8, L is the minimum characteristic length of element, c is the fastest wave velocity in a material. For an isotropic elasto- plastic material, the elastic wave velocity v_e and the plastic wave velocity v_p can be expressed as[5]

where  E is elastic modulus,  is Poisson ratio, ρ is mass density, E_T (=dσ/dε) is the slope of the stress—strain curve at plasticity stage, σ and ε are stress and strain, respectively. It is clear that the elastic wave velocity is larger than that of plastic wave because of E_T＜E. Hence, the elastic wave velocity was used to calculate the maximal time increment in numerical simulations.

The time increment calculated according to Eqn.(5) is very short, and this is the reason why the central difference scheme is usually used to analyze the stress wave propagation.

2.2 Calculation of hammer velocity

During analyzing the fast upsetting process under drop hammer impact by the dynamic explicit finite element method, the hammer velocity must be calculated in each time increment step in order to apply the velocity boundary condition for the workpiece. Energy transformation controls the deformation process during drop hammer impact. The initial kinetic energy of hammer transfers into the deformation energy of workpiece, and hammer velocity is changed and unknown.

According to the operating principle of drop hammer, the blow energy E₀, blow efficiency η and hammer mass m are input parameters of the equipment in the finite element model. During the deformation, the kinetic energy of hammer transfers into deformation energy of workpiece E_d, hammer velocity v decreases with the increase of deformation time, and is calculated by energy conservation law.

At the beginning, the impact velocity is calculated according to the blow energy E₀ and hammer mass m:

In each time increment step, the deformation energy of workpiece is calculated by incremental method:

According to energy conservation law, the remaining energy can be expressed as follows:

If E_n＞0, the hammer velocity is calculated by the following equation:

Otherwise, the calculation is stopped, and the deformation process is completed.

2.3 Treatment of contact interface

A contact-searching scheme based on a master-slave algorithm[14] is used to treat the contact interface. The die and workpiece are considered as master and slave body, respectively. Normal contact force is calculated by penalty method. The frictional contact condition encountered in three-dimensional metal forming processes is quite complex. In order to model the frictional phenomena precisely, the non-classical Coulomb friction law is implemented in the code[16].

3 Finite element analysis of fast upsetting process

3.1 FEA model and calculation condition

The dimension of initial block is 240 mm×240 mm ×120 mm. The equipment parameters of drop hammer are as follows: blow energy 250 kJ, blow efficiency 0.8 and hammer mass 2 200 kg. Industrial pure lead, OFHC copper and 7039 aluminum alloy are chosen as simulation materials. The material parameters and the flow stress models are shown in Tables 1 and 2, respectively. Due to the symmetry of the deformation process, only one quarter of the block is adopted for the finite element analysis, as shown in Fig.1. OZ is symmetry axis, and the constrained displacements are applied to the symmetry surfaces at X=0 and Y=0. In order to investigate the effect of stress wave more  clearly, an ideal condition that the frictional coefficient is zero is considered.

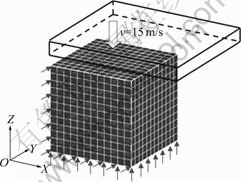
Fig.1 Finite element analysis model

Table 1 Parameters of material[17-18]

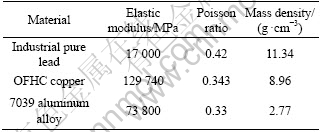
Table 2 Flow stress model of materials[18-19]

3.2 Elastic wave analysis

The initial time is defined as t=0 at which the hammer contacts the top surface of the block. In order to investigate the elastic wave propagation, the stress distribution along Z direction σ_Z at the initial deformation stage is analyzed (as shown in Fig.2). The elastic wave firstly acts on the top surface and propagates along the -Z direction. For industrial pure lead, OFHC copper and 7039 aluminum alloy, the elastic waves arrive on the bottom surface of the block after 0.61×10^-4, 0.26×10^-4 and 0.20×10^-4 s, respectively, by which the elastic wave velocity obtained are 1.96×10⁶, 4.62×10⁶ and 6.00×10⁶ mm/s, respectively. Once traveling to the bottom surface of the block, the elastic wave reflects and returns towards the upper surface.

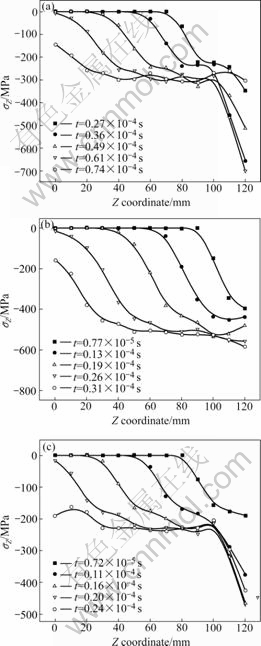
Fig.2 Stress distribution along Z direction at early deformation stage: (a) Industrial pure lead; (b) OFHC copper; (c) 7039 aluminum alloy

The theoretical value of elastic wave velocities can be obtained by applying the material parameters to Eqn.(6), as listed in Table 3, which are in good agreement with the calculated results of finite element analysis.

Table 3 Theoretical and calculated values of elastic wave velocity

3.3 Plastic wave analysis

When the applied stress is sufficient to produce plastic deformation in the block, plastic wave will emerge. For the each time incremental step during the initial stage of deformation, the distribution of equivalent plastic strain is analyzed. When the material points in the top region of block first generate plastic deformation, plastic wave begins to propagate. For the three materials, the plastic wave begins to propagate in the deformed blocks at about 0.14×10^-4, 0.58×10^-5 and 0.86×10^-5 s, respectively. The plastic wave propagation can be analyzed by the equivalent plastic strain distribution in the block at the initial deformation stage, as illustrated in Fig.3. The plastic wave first acts on the top surface and propagates along the -Z direction. Once traveling to the upper surface or the bottom surface, the plastic wave will reflect.

Fig.3 Equivalent plastic strain distribution at early deformation stage: (a) Industrial pure lead; (b) OFHC copper; (c) 7039 aluminum alloy

The locations of wave fronts at three specific moments are illustrated in Figs.4, 5 and 6, respectively. The plastic wave fronts lag behind the elastic wave fronts all the time. When the elastic wave fronts travel to the bottom surface, the plastic wave fronts arrive at the location of Z=20, 30 and 90 mm, respectively. For industrial pure lead and OFHC copper, the plastic wave front travels to the bottom surface at 0.74×10^-4 and 0.37×10^-4 s, as shown in Figs.4(c) and 5(c), respectively, and the corresponding equivalent plastic strain distribution is shown in Figs.7(a) and (b). For 7039 aluminum alloy, the material points at the bottom generate plastic deformation at 0.3×10^-4 s and the plastic strain in lower region of the block increases quickly, as shown in Fig.7(c), which implies that another plastic wave reflects from the bottom surface and propagates towards the upper surface at this moment, as shown in Fig.6(c).

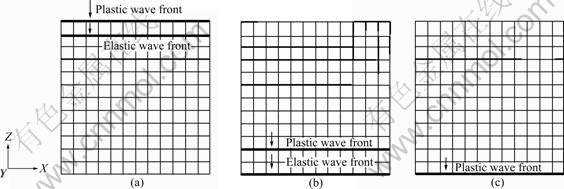
Fig.4 Location of elastic wave front and plastic wave front for industrial pure lead: (a) t=0.14×10^-4 s; (b) t=0.61×10^-4 s; (c) t=0.74×10^-4 s

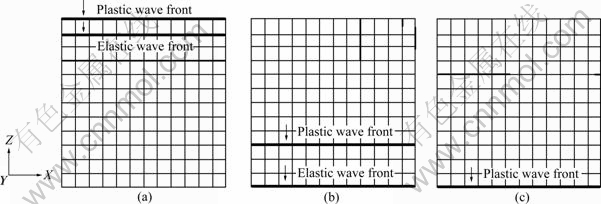
Fig.5 Location of elastic wave front and plastic wave front for OFHC copper: (a) t=0.58×10^-5s; (b) t=0.26×10^-4 s; (c) t=0.37× 10^-4 s

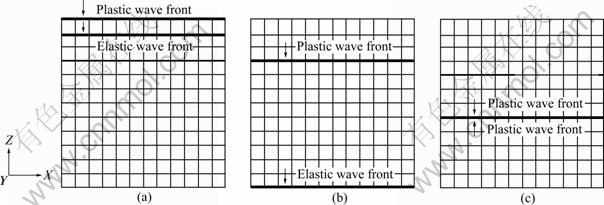
Fig.6 Location of elastic wave front and plastic wave front for 7039 aluminum alloy: (a) t=0.86×10^-5 s; (b) t=0.2×10^-4 s; (c) t=0.3×10^-4 s

Fig.7 Equivalent plastic strain distribution when plastic wave front arrived at bottom: (a) Industrial pure lead; (b) OFHC copper; (c) 7039 aluminum alloy

Assuming that the density ρ keeps constant during the deformation, the plastic wave velocity v_p depends on the slope of stress—strain curve E_T. For the three materials, E_T is continuously changed and decreases with the increase of equivalent plastic strain ε_p. The plastic wave velocity v_p can be obtained by applying the material parameters and flow stress model to Eqn.(7), as shown in Fig.8. The plastic wave velocity v_p decreases with the increase of equivalent plastic strain ε_p, and the theoretical values are roughly 0.39×10⁵-1.224×10⁶, 0.67×10⁵-3.81×10⁶ and 1.38×10⁵-5.16×10⁶ mm/s for the three materials, respectively.

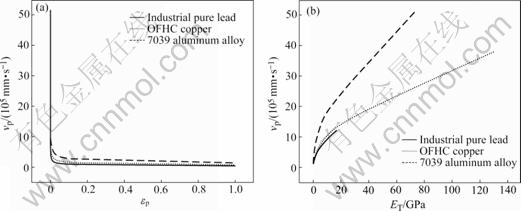
Fig.8 Theoretical values of plastic wave velocity: (a) ε_p—ν_p curve; (b) E_T—ν_p curve

For the three materials, there is a great difference in the equivalent plastic strain distribution at t=4.6×10^-3 s, as shown in Fig.9. For industrial pure lead, the distribution is non-uniform, and the plastic strain concentration zone occurs in the upper region of the block. The distribution of equivalent plastic strain in the copper block is more uniform than that in the lead block. By contrast, the distribution in 7039 aluminum alloy block is most uniform. The non-uniform distribution of equivalent plastic strain is the result of the stress wave propagation and reflection in the block. It can be concluded that the influence of stress wave on the deformation is the most obvious in the lead block, and the smallest in the 7039 aluminum alloy block.

Fig.9 Equivalent plastic strain distribution in block at time of 4.6×10^-3 s: (a) Industrial pure lead; (b) OFHC copper; (c) 7039 aluminum alloy

For the same blocks, there is a large difference in the stress wave velocity among the three materials, which makes stress wave have a different influence on the deformation. With the increase of stress wave velocity, the numbers of stress wave reflection in the block increase, and the influence of stress wave on the deformation becomes weaken, which can be explained from two aspects: 1) the hammer velocity continuously decreases with the deformation time, and then the wave front propagates with smaller stress value; 2) the effect of incoming wave and reflected wave counteracts each other. On impact, a stress wave of compression is propagated along the top surface of block. This wave travels to the bottom surface of block, which is reflected as a wave of tension, and returns towards the top surface, relieving the compressive stress produced by the incoming wave.

For industrial pure lead, OFHC copper and 7039 aluminum alloy, the fast upsetting deformation processes are completed at 7.0×10^-3, 7.8×10^-3 and 6.7×10^-3 s, respectively. At the final stage, the stress distribution along Z direction is approximately uniform, as shown in Fig.10. This indicates that at the middle-final forming stage, many times of reflection in the block occur to the stress wave, which makes the oncoming wave and return wave counteract each other. Therefore, stress wave has little effect on the deformation, and the distribution of stress and strain becomes uniform.

Fig.10 Stress distribution along Z direction at final deformation stage: (a) Industrial pure lead; (b) OFHC copper; (c) 7039 aluminum alloy

1) A finite element code is developed based on the energy method and dynamic explicit algorithm. The stress wave propagation during the fast upsetting process can be analyzed using the developed code. The calculated stress wave velocity is in good agreement with the theoretical value, which verifies the effectiveness of developed code.

2) During the fast upsetting, the deformation process can be represented by the stress wave propagation and reflection. There are two stress waves with different propagation velocities. The quicker one is elastic wave, and the slower one is plastic wave. Stress wave has an important effect on the uniformity of deformation, which makes stress and strain distribution exhibit propagation characteristic. Stress wave propagation has a significant effect on the deformation at the initial stage, and then becomes weak at the middle- final stage.

3) The material parameters have a significant influence on the stress wave velocity. With the increase of E/ρ and E_T/ρ, the velocity of stress wave propagation increases, and the effect of stress wave propagation on the deformation becomes weak.

[1] RADFORD D D, WALLEY S M, CHURCH P, FIELD J E. Dynamic upsetting and failure of metal cylinders—Experiments and analysis [J]. Journal De Physique IV, 2003, 110: 263-268.

[2] DIOT S, GUINES D, GAVRUS A, RAGNEAU E. Two-step procedure for identification of metal behavior from dynamic compression tests [J]. International Journal of Impact Engineering, 2007, 34: 1163-1184.

[3] RAO K P, JAGASIVAMANI V, GOPINATHAN V, DORAIVELU S M. A gravity drop hammer for high velocity deformation studies of materials [J]. International Journal of Machine Tool Design and Research, 1985, 25(1): 51-62.

[4] CAMPBELL J D. Dynamic plasticity: Macroscopic and microscopic aspects [J]. Materials Science and Engineering, 1973, 12: 3-21.

[5] KOLSKY H, DOUCH L S. Experimental studies in plastic wave propagation [J]. J Mech Phys Solids, 1962, 10: 195-223.

[6] CLIFTON R J. Stress wave experiments in plasticity [J]. International Journal of Plasticity, 1985, 1: 289-302.

[7] LEE L H, WOLF H. Plastic-wave propagation effects in high speed testing [J]. ASME Journal of Applied Mechanics, 1951, 18: 379-386.

[8] ALBERTINI C, MONTAGNANI M. Wave propagation effects in dynamic loading [J]. Nuclear Engineering and Design, 1976, 37: 115-124.

[9] HAN Zhi-jun, CHENG Guo-qiang, MA Hong-wei, ZHANG Shan- yuan. Dynamic buckling of elastic-plastic column impacted by a rigid body [J]. Applied Mathematics and Mechanics, 2006, 27(3): 337-341.

[10] LI Yong-chi, ZHU Lin-fa, HU Xiu-zhang, YUAN Fu-ping, CAO Jie-dong. Study on propagation properties of combined stress waves in viscoplastic thin-walled tubes [J]. Explosion and Shock Waves, 2003, 23(1): 1-5.

[11] SUN Yu-xin, ZHANG Jin, LI Yong-chi, HU Shi-Sheng, DONG Jie. Propagation of stress wave and spallation of cylindrical tube under external explosive loading [J]. Chinese Journal of High Pressure Physics, 2005, 19(4): 319-324.

[12] LEE E H, TUPPER S J. Analysis of plastic deformation in a steel cylinder striking a rigid target [J]. Journal of Applied Mechanics, 1954, 21: 63-70.

[13] ARGYRIS J H, CHAN A S L. Applications of finite elements in space and time [J]. Ingenieur-Archiv, 1972, 41: 235-257.

[14] HALLQUIST J O. Ls-dyna theoretical manual [M]. California: Livermore Software Technology Corporation, 1998: 28-30, 370- 374.

[15] SUN J S, LEE K H, LEE H P. Comparison of implicit and explicit finite element methods for dynamic problems [J]. Journal of Materials Processing Technology, 2000, 105: 110-118.

[16] ZHONG Z H. Finite element procedures for contact–impact [M]. New York: Oxford University Press, 1993: 141-144.

[17] XU Xiu-mei, ZHANG Wen-zhi, ZONG Jia-fu. Simulation and study on universal rolling process of rail by 3-dimension elastic-plastic finite element method [J]. Metallurgical Equipment, 2004, 148(6): 1-3, 27.

[18] JOHNSON G R, COOK W H. A constitutive model and data for metals subjected to large strain rates and high temperature [C]// Proceedings of the 7th International Symposium on Ballistics. Hague, Netherlands, 1983: 541-547.

[19] LI Miao-quan. On the constitutive relationship and the limitation of lead used as model material [J]. Metal Science & Technology, 1987, 6(3): 102-107.

Corresponding author: WANG Zhong-jin; Tel: +86-451-86413365; E-mail: wangzj@hit.edu.cn

(Edited by LI Xiang-qun)