文章编号:1004-0609(2010)04-0662-05
TP2铜与3Cr2W8V模具钢的瞬态接触换热系数
邢 磊,张立文,张兴致,岳重祥
(大连理工大学 材料科学与工程学院,大连 116085)
摘 要:基于反传热算法,制造一套瞬态接触换热系数测量装置,研究高温TP2铜与低温3Cr2W8V模具钢的瞬态接触换热过程。结果表明:接触载荷在1.56~7.80 MPa范围内变化时,高温TP2铜的初始温度为400、500和600 ℃,低温3Cr2W8V模具铜的初始温度为100、200和300 ℃。瞬态接触换热系数在很短时间内(5 s)快速增大到某一恒定值,并随着时间延长,产生缓慢的后续增加过程。接触换热系数随着接触载荷的增加而增大,呈幂指数关系,且试样初始温度越高,接触换热系数增大的趋势越快。
关键词:TP2铜;3Cr2W8V模具钢;瞬态法;反传热算法;接触换热系数
中图分类号:TG113.2 文献标志码:A
Transient contact heat transfer coefficient between
TP2 copper and 3Cr2W8V die steel
XING Lei, ZHANG Li-wen, ZHANG Xing-zhi, YUE Chong-xiang
(School of Materials Science and Technology, Dalian University of Technology, Dalian 116085, China)
Abstract: Based on the principle of inverse heat transfer problems, a new experimental apparatus was developed to measure the contact heat transfer coefficient in the transient condition. The transient contact heat transfer was investigated between the hot TP2 copper and cold 3Cr2W8V steel. The results show that the contact pressure is in the range of 1.56-7.80 MPa, the initial temperatures of the hot TP2 copper are 400, 500 and 600 ℃, and the initial temperatures of the cold 3Cr2W8V steel are 100, 200 and 300 ℃. The contact heat transfer coefficient increases rapidly to a level in a very short time (5 s), from which a much slower increase occurs. The contact heat transfer coefficient increases with increasing contact pressure according to the power law correlation, and it is relatively high at high initial temperature.
Key words: TP2 copper; 3Cr2W8V steel; transient method; inverse heat transfer method; contact heat transfer coefficient
TP2铜具有良好的导电导热性、抗磁性和抗大气腐蚀性,因此,TP2铜管被广泛地应用于空调和冰箱制冷管、热交换器用管、蒸汽管和蒸馏装置用管等[1-2]。在铜管铸坯的轧制过程中,坯料与轧辊间的接触换热系数影响着铜管的质量和轧辊的使用寿命,接触换热系数也是影响铜管轧制过程数值模拟结果准确性的关键参数[3-4]。
近年来,国内外学者采用稳态热流法对不同材料间接触换热系数进行研究,获得一些有价值的实验数据[5-10]。实际热加工是坯料与工模具的瞬态接触过程,温度场在极短时间内发生剧烈变化,其物理机制与稳态过程有一定差别,因此,有必要对金属界面间瞬态接触换热过程进行研究。BECK等[11]分析这种瞬态接触,给出界面平均温度的解析表达式,并采用非稳定表面元(USE)法求解线性瞬态接触换热问题。FIEBERG等[12]利用红外测温仪对不同温度的钢与铝合金接触后的瞬态温度场进行测量,求解瞬态热传导方程得到接触换热系数。目前,国外对瞬态接触换热过程的研究甚少,且测量温度较低(<280 ℃),国内关于这方面的研究尚未见报道。
本文作者基于反传热算法,制造一套瞬态接触换热系数测量装置,研究TP2铜与3Cr2W8V模具钢之间的瞬态接触换热过程,探讨不同初始温度与不同接触载荷条件下接触换热系数的变化规律,为铜管轧制及其数值模拟研究提供数据参考。
1 实验
将TP2铜铸坯及3Cr2W8V模具钢材料加工成尺寸为d 20 mm×50 mm的圆柱试样,试样侧面沿轴线方向打3个d 1.0 mm×10 mm的热电偶插孔,分别作为近表面测点、校核测点与内部测点,距离待接触面距离分别为1、11和21 mm,实验前用400#砂纸将试样接触面打磨平整。实验采用经校准的d1.0 mm镍铬-镍硅裸端式热电偶进行测温,响应时间约为0.01 s。
实验测量装置如图1所示,整个装置主要由4部分组成,包括加热系统、传动机构、加载机构和温度采集系统。加热系统最高加热温度能够达到 1 000 ℃,最大实验载荷可达30 MPa。带自动增益的高速A/D转换卡通过16通道的前端放大板将测温热电偶信号输入采集软件,实现模拟量与数字量的转换。
实验时,试样外侧缠绕隔热石棉布,尽量减少对流和辐射传热对试样温度的影响。试样分别置于高温与低温加热炉加热到一定的温度,保温一段时间,使试样初始温度分布均匀,然后通过传动机构使两试样

图1 接触换热系数测量装置示意图
Fig.1 Schematic diagram of heat transfer coefficient test apparatus: 1—Transmission mechanism; 2—Resistance furnace; 3—Specimen; 4—Load mechanism; 5—Supporting part; 6—Industrial computer; 7—PCL-789D amplifier board; 8—Thermocouples for measurement; 9—Thermocouples for controlling; 10—AI thermometer
快速接触,加载机构会使预先设定的载荷逐渐施加在接触面上并保持一定时间,与此同时,温度采集系统通过测温热电偶、前端放大板、A/D转换板将温度信号实时显示在工控机内的数据采集软件上。
2 反传热问题求解
由于瞬态接触和稳态接触在物理过程上的差异,不能采用线性外推法[6]进行计算。考虑到试样外侧近似绝热效果,根据Beck提出的非线性估算方法[13-15],建立一维瞬态热传导的数学模型,由试样近表面测点与内部测点的温度测量值计算接触表面上的温度与热流密度。其温度场T(x,t)的控制方程为

式中:模型长度L取为21 mm;瞬时热流密度qM在tM-1和tM时刻之间为常数;ρ、c和k分别为材料的密度、比热容和热导率;TM-1(x)为试样在tM-1时刻的温度分布,Tw(tM-1)为内部测点的温度值。定义敏感系数为温度关于热流密度的一阶微商,如式(2)所示,表示对近表面温度测量误差的敏感程度。
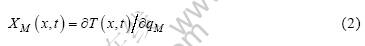
由此可见,敏感系数场和温度场具有相同形式的微分方程,可通过有限差分方程进行求解,对任意给定的热流密度q*进行泰勒级数展开可得:

式中:TM为近表面测点在tM时刻的温度;YM是在tM-1时刻温度场已知的情况下,根据q*求解的tM时刻的温度,XM为近表面测点在tM时刻的敏感系数,对式(3)进行反复迭代运算即可得到qM。
瞬态条件下,接触换热系数hc可由式(4)得到:

式中:q′M与ΔTM分别为tM-1和tM时刻之间的界面平均热流密度和温差。
3 结果与讨论
利用上述实验装置,对TP2铜与3Cr2W8V模具钢试样接触过程进行测量,高温铜试样初始温度分别为400、500、600 ℃,对应低温模具钢试样温度分别为100、200、300 ℃,实验载荷范围为1.56~7.80 MPa。
3.1 温度场验证
初始试样温度分别为600 ℃和300 ℃,接触载荷为4.68 MPa时,近表面测点温度值与表面温度推算值如图2所示。
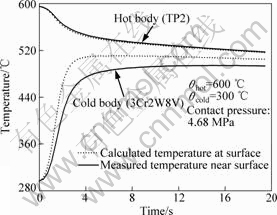
图2 试样表面及近表面测点温度随时间的变化
Fig.2 Change of temperature at surface and near surface of test specimens with time
由图2可见,接触面温度在接触后5 s内发生剧烈变化,由于两种材料热物性的差异,模具钢热导率低,热量来不及向后传递,试样温度快速上升至 510 ℃,并且表面与近表面测点存在较大温差,高热导率的铜试样温度变化则相对缓慢,表面温度与近表面测点温度基本相同。图3所示为校核测点温度测量值与计算值比较。由图3可看出,二者吻合较好,温度偏差主要是测量与计算的误差所致,这一结果表明数据采集方法与反传热问题的求解是合理的。
3.2 瞬态接触换热系数
图4所示为为流密度随时间的变化。从图4中可看出,热流密度在接触后1.5 s后就达到峰值1.44 MW/m2,然后迅速下降;5 s后,热流密度的下降趋势开始变得缓慢,说明接触载荷由0增加至4.68 MPa的时间为1.5 s,接触界面间剧烈的热量交换在5 s内

图3 校核测点温度测量值与计算值比较
Fig.3 Comparison of calculated and measured temperature at verification position
已经基本完成。接触换热系数在这段时间内快速上升至恒定值27.331 kW/(m2·℃)(见图5)。由图5可看出,由于载荷的作用,接触表面上的微小接触体将发生弹性或塑性变形,使实际接触面积增大,界面换热能力提高。从曲线上看,接触换热系数存在一定程度的波动,且随着时间的延长,波动幅度变大。原因有如下两个方面:1) 温度信号采集速度较快,相邻时刻的温度测量值会产生波动,外界干扰对温度数据也会产生一定影响;2) 随着时间增加,界面温差及热流密度逐渐减小,计算误差增大。平滑滤波后发现,接触换热系数在5 s后呈现后续的缓慢增加趋势,这是因为高温试样的屈服强度下降,接触表面的微小接触体在原有变形的基础上,继续发生缓慢变形,进一步增大实际接触面积。

图4 热流密度随时间的变化
Fig.4 Change of heat flux with time
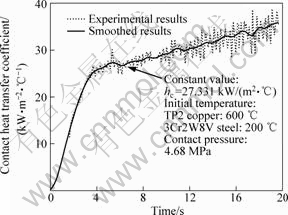
图5 接触换热系数随时间的变化
Fig.5 Change of contact heat transfer coefficient with time
3.3 载荷对接触换热系数的影响
图6所示为试样初始温度分别为600和300 ℃时不同压强条件下接触换热系数随时间的变化。由图6可看出,随着接触载荷的增加,表面微小接触体的变形程度增大,实际接触面积增加,换热能力增强,界面间温差变小,热流密度增大,因此,接触换热系数随着载荷的增加逐渐变大。从图6还可看出,b线(3.12 MPa)与c线(4.68 MPa)之间接触换热系数的变化幅度相对较大,当压强大于4.68 MPa时,接触换热系数随时间的后续增加趋势明显,这说明接触换热系数可能受其他因素影响,对较小载荷的变化不敏感,当载荷达到某一临界值时,才能起主导作用。
图7所示为试样在不同初始温度条件下5 s时接触换热系数随压强的变化关系。根据文献[16]的结果,接触换热系数随接触压强的变化呈幂指数关系,即

图6 不同压强下接触换热系数随时间的变化
Fig.6 Change of contact heat transfer coefficient with time at different contact pressures

图7 接触换热系数随压强的变化
Fig.7 Change of contact heat transfer coefficient with contact pressure
hc~pn。对实验压强范围内的各组数据进行幂指数拟合后发现,结果吻合较好,对于不同的初始温度,曲线幂指数是不同的,温度越高,指数值越大,接触换热系数增加速率也越快。当载荷小于3.12 MPa时,接触换热系数值对曲线产生一定偏离,这主要是因为铜在高温下非常容易氧化,实验发现,600 ℃时接触表面将产生厚度约为50 μm的氧化层,当载荷较小时,接触表面变形程度低,实际接触面积小,而氧化层的隔热作用显著,二者的综合作用导致了上述现象的产生。
4 结论
1) 制造一套瞬态接触换热系数测量装置,获得TP2铜与3Cr2W8V模具钢试样在不同初始温度与不同接触载荷条件下的瞬态接触换热系数。
2) 通过校核测点温度测量值与计算值的对比,验证实验的合理性与计算的准确性。
3) 在瞬态条件下,接触换热系数随接触时间的延长而快速增大到某一恒定值,并产生后续的缓慢增加过程。
4) 在实验载荷范围内,接触换热系数随接触载荷增加而增大,呈幂指数关系,试样初始温度越高,接触换热系数增大速率越快。
REFERENCES
[1] 肖 寒, 张士宏, 张海渠, 张立文. TP2铜管坯水平连铸缺陷检测及分析[J]. 铸造, 2006, 55(3): 271-275.
XIAO Han, ZHANG Shi-hong, ZHANG Hai-qu, ZHANG Li-wen. Detection and analysis of the defects for horizontal continuous casting of TP2 copper tube billets[J]. Foundry, 2006, 55(3): 271-275.
[2] 杨晓静, 孙方宏, 张志明, 沈荷生, 郭松寿. 基于有限元模拟的空拔铜管拉拔参数的优化[J]. 中国有色金属学报, 2008, 18(12): 2245-2252.
YANG Xiao-jing, SUN Fang-hong, ZHANG Zhi-ming, SHEN He-sheng, GUO Song-shou. Optimization of drawing parameters for copper tubes with hollow sinking based on FEM simulation[J]. The Chinese Journal of Nonferrous Metals, 2008, 18(12): 2245-2252.
[3] 陈晓健. 铜管四辊行星轧制工艺有限元模拟研究[D]. 大连: 大连理工大学, 2008: 29-36.
CHEN Xiao-jian. Research on finite element simulation of four-roll planetary rolling process of copper tubes[D]. Dalian: Dalian University of Technology, 2008: 29-36.
[4] 杨 志. 三辊行星轧制铜管的有限元数值模拟[D]. 阜新: 辽宁工程技术大学, 2003: 45-49.
YANG Zhi. Finite element numerical simulation on three-roll planetary rolling process of copper tubes[D]. Fuxin: Liaoning University of Engineering Technology, 2003: 45-49.
[5] ROSOCHOWSKA M, CHODNIKIEWICZ K, BALENDRA R. A new method of measuring thermal contact conductance[J]. Journal of Materials Processing and Technology, 2004, 145(2): 207-214.
[6] ROSOCHOWSKA M, BALENDRA R, CHODNIKIEWICZ K. Measurements of thermal contact conductance[J]. Journal of Materials Processing and Technology, 2003, 135(2/3): 204-210.
[7] LAMBERT M A, MIRMIRA S R, FLETCHER L S. Design graphs for thermal contact conductance of similar and dissimilar light alloys[J]. Journal of Thermophysics and Heat Transfer, 2006, 20(4): 809-816.
[8] BAHRAMI M, YOVANOVICH M M, CULHAM J R. Thermal contact resistance at low contact pressure: Effect of elastic deformation[J]. International Journal of Heat and Mass Transfer, 2005, 48(16): 3284-3293.
[9] 张立文, 朱德才, 邢 磊, 张国梁, 韦荣选. 铝合金与5CrMnMo模具钢界面接触换热系数实验研究[J]. 大连理工大学学报, 2009, 49(1): 60-64.
ZHANG Li-wen, ZHU De-cai, XING Lei, ZHANG Guo-liang, WEI Rong-xuan. Experimental measurement on thermal contact conductance coefficient between aluminum alloys and 5CrMnMo die steel[J]. Journal of Dalian University of Technology, 2009, 49(1): 60-64.
[10] 赵兰萍, 徐 烈. 低温真空下固体界面间接触导热的实验研究[J]. 中国空间科学技术, 2003, 23(1): 51-55.
ZHAO Lan-ping, XU Lie. Experimental research on the heat transfer between the solid interfaces at low temperatures and vacuum[J]. Chinese Space Science and Technology, 2003, 23(1): 51-55.
[11] BECK J V, KELTNER N R. Transient thermal contact of two semi-infinite bodies over a circular area[J]. Spacecraft Radiative Transfer Temperature Control, 1982, 83(1): 61-80.
[12] FIEBERG C, KNEER R. Determination of thermal contact resistance from transient temperature measurements[J]. International Journal of Heat and Mass Transfer, 2008, 51(5/6): 1017-1023.
[13] BECK J V, BLACKWELL B, CLAIR C R S T. Inverse heat conduction, ill-posed problems[M]. New York: Wiley-Verlag, 1985.
[14] 顾剑锋, 潘健生, 胡明娟. 淬火冷却过程中表面综合换热系数的反传热分析[J]. 上海交通大学学报, 1998, 32(2): 19-31.
GU Jian-feng, PAN Jian-sheng, HU Ming-juan. Inverse heat conduction analysis of synthetical surface heat transfer coefficient during quenching process[J]. Journal of Shanghai Jiao Tong University, 1998, 32(2): 19-31.
[15] 杨 冬, 陈听宽. 导热反问题方法在计算瞬态传热过程中的应用[J]. 核动力工程, 1997, 18(6): 553-559.
YANG Dong, CHEN Ting-kuan. Application of inverse heat conduction problem in transient heat transfer calculating[J]. Nuclear Power Engineering, 1997, 18(6): 553-559.
[16] JAIN V K. Determination of heat transfer coefficient for forging applications[J]. Journal of Materials Shaping Technology, 1990, 8(3): 193-202.
(编辑 李艳红)
收稿日期:2009-05-12;修订日期:2009-09-10
通信作者:张立文,教授,博士;电话:0411-84706087;E-mail:commat@mail.dlut.edu.cn