文章编号: 1004-0609(2005)03-0338-06
铜薄板连铸过程中的温度场模拟
李金山, 梅金娜, 陈忠伟, 胡 锐, 寇宏超
(西北工业大学 凝固技术国家重点实验室, 西安 710072)
摘 要: 基于傅立叶导热微分方程, 建立了薄板坯连铸过程中凝固传热的数学模型, 编制了预测连铸过程中温度场分布的计算机模拟程序。 利用该程序计算了不同拉速及冷却条件下, 铜薄板连铸过程中温度场的分布, 并分析了拉速、 冷却条件对铸坯温度的影响。 模拟结果表明: 拉速提高, 出坯温度明显升高, 因此为了防止拉漏, 关键是选择合理的拉速; 同时, 冷却条件也是影响结晶器温度场分布的重要工艺参数之一; 模型计算得出的铸坯温度与实测值基本相符, 温度误差在10℃以下, 计算结果可优化连铸工艺参数。
关键词: 薄板; 连铸; 温度场; 拉速; 冷却条件
中图分类号: TF777.7 文献标识码: A
Numerical simulation of temperature field in
continuous casting of copper thin-slab
LI Jin-shan, MEI Jin-na, CHEN Zhong-wei, HU Rui, KOU Hong-chao
(State Key Laboratory of Solidification Processing,
Northwestern Polytechnical University, Xian 710072, China)
Abstract: A mathematical model to represent the solidification heat transfer process of thin-slab continuous casting and a computer simulation program based on Fourier conduction differential equation were worked out, which can be applied to predict the distribution of temperature field during the process of continuous casting. This program was applied to calculate the temperature distribution of copper thin-slab continuous casting with different casting speeds and cooling conditions. In the meantime, the effects of casting speed and cooling condition on thermal profile were studied. Simulation experiments show that the surface temperature out of the mould can be increased significantly by improving the casting speed. So in order to prevent the thin-slab from leaking, choosing casting speed correctly is a sticking point. Additionally, cooling condition is one of the important technological parameters as well as casting speed. The results show that the thermal profile calculated by mathematical model almost agrees with those obtained by experimental measurement, and the error is within 10℃.
Key words: thin-slab; continuous casting; temperature field; casting speed; cooling condition
随着现代连铸工艺的日趋完善, 连铸已成为钢材生产的主要方法。 连铸薄板坯的质量和生产成本很大程度上依赖于连铸生产工艺。 连铸薄板技术是近年来该学科发展的前沿领域[1-3], 其传热过程的温度场数值计算是该领域的重点和难点。 因此, 如何选取最优工艺参数, 制定合理的生产制度, 是提高薄板铸坯质量的核心技术问题[2-4]。
张炯明等[4]采用数学分析方法对板坯连铸结晶器的热流量及结晶器和冷却水之间的传热进行了详细的分析; 崔立新等[5]研究了连铸板坯在结晶器内的凝固行为; 张富强等[6]研究了中薄板坯高拉速连铸结晶器的平均热流。 然而, 由于连铸条件下的凝固过程难以直接观察或进行实验研究, 因此, 随着计算机的发展和数值计算技术的不断成熟, 借助于计算机数值模拟技术便成为研究连铸凝固过程以及指导连铸生产的重要手段[7-12]。
1 薄板坯连铸传热数学模型
1.1 铸坯传热过程的计算假设[13, 14]
1) 铸坯的传热计算视为一维非稳态导热, 忽略沿铸坯移动方向上的传热;
2) 液态金属均一, 不考虑其内部的传热;
3) 忽略振动对凝固过程传热的影响;
4) 铸坯几何对称面的传热相同, 计算区域可做几何对称处理;
5) 铜的热物性参数与温度相关, 与空间位置无关。
1.2 凝固传热微分方程
在上述假设条件的基础之上, 根据能量守恒原理推导出传热方程[15]如下:
式中 T为温度, K; t为时间, s; x为坐标, m; ρ为金属密度, kg/m3; c为金属比热容, J/(kg·K); λ为金属导热系数, W/(m·K)。
1.3 初始条件
将初始条件定为浇铸温度, 即: t=0时, T=T0 (T0为浇铸温度, K)。
1.4 边界条件
1) 结晶器内
结晶器导出热流取决于拉坯速率、 熔体过热度、 结晶器变形、 结晶器的振动等多种因素, 研究表明, 对于不同的结晶器, 静止冷却时测定的瞬时热流与熔体停留的关系可表示为[15]:
式中 q1为边界上各节点的温度沿边界法向n的热流率; A为结晶器入口截面上的热流密度, W/m2; B为经验常数; τ为铸坯运行到结晶器某一位置所对应的时间, s。
因为
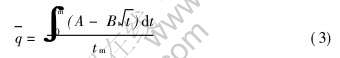
式中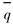 
为平均热流; tm为铸坯在结晶器内的停留时间, s。
又因为
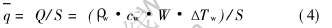
式中 ρw为冷却水密度, g/cm3; cw为冷却水比热容, J/(g·K); W为水流量, cm3/s; ΔTw为结晶器进出水温差, K; S为铸坯与结晶器的接触面积, cm2。
将式(4)带入式(3), 可计算出B值。
2) 二冷区
热流密度为:
q2=α(Ts-Tw)(5)
式中 α为二冷区的综合传热系数, W/(m2·K); Ts为铸坯表面温度, K; Tw为冷却水温度, K。
3) 空气冷却区
热流密度为[14]:
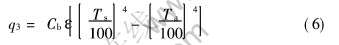
式中 Cb为黑体辐射系数, W/(m2·K4); ε为有效黑度;Ta为环境空气温度, K。
1.5 热物性参数的处理
1) 不同相区密度取为不同的常数。
2) 考虑到温度对导热系数的影响, 用有效导热系数λeff代替导热系数λ。 有效导热系数λeff为温度T的线形函数[16], 即:
λeff=a+bT(7)
式中 a、 b为常数。
3) 不同相区比热容取为不同的常数。
1.6 凝固潜热的处理
凝固潜热是指从液相线到固相线温度所放出的热量, 凝固潜热的处理一般有等效热容法、 转化热焓法和温度回升法[17], 对于纯金属或共晶合金等在一定温度下凝固的金属, 则采用所谓温度回升法模拟释放潜热的过程。 因此本模型凝固潜热的处理采用温度回升法。
对于体积为ΔV的金属单元, 在凝固阶段需要补偿的温度值为:
ΔT=L/c(8)
式中 L为铜的熔化热。
2 传热数学模型的求解
2.1 节点差分方程
这里, 我们采用有限差分法进行数值计算。 由于板坯具有对称性, 因此沿板坯厚度方向选取板坯的二分之一进行研究。 将铸坯网格化, 自铸坯中心算起, 把铸坯分为M等分, 则有m=1, 2, 3, …, M+1, 共有M+1个节点。
1) 内部节点
用直接替代法推导内部节点差分方程为:
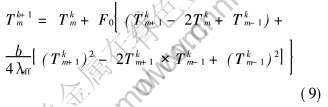
式中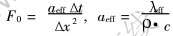 
, Δx为空间步长。
2) 边界节点
边界节点的差分方程, 按边界上半层的近似热平衡式导出为:
式中 q值分别由式(2)、 (5)和(6)计算得到。
3) 中心节点
中心节点温度Tk+11可由式(9)确定。 中心节点的差分方程为:
Tk+11=Tk1+2F0(Tk2-Tk1)(11)
4) 稳定性条件[16]
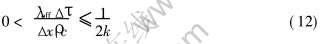
式中 k为非线性修正系数, 取1~2; 经计算, 选取时间步长(单位: s)为Δτ=2×10-5。
2.2 程序的编制
程序是在window XP操作系统上, 采用C++程序语言编制的。 图形显示应用Compaq Array Visualizer软件。 图1所示为程序流程图。
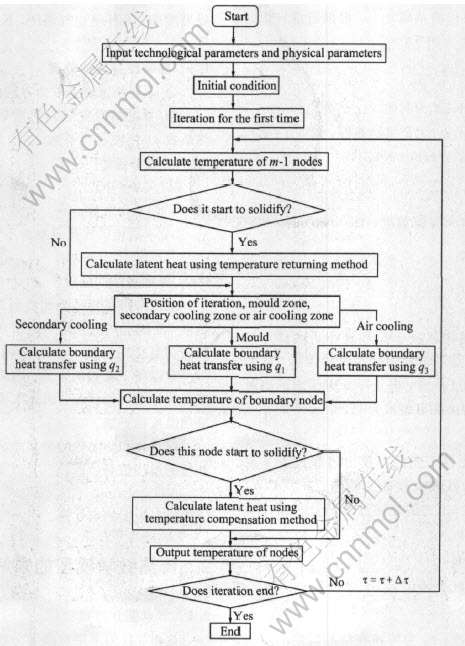
图1 程序流程图
Fig.1 Flow chart
3 计算结果与分析验证
3.1 计算用参数列表(如表1)
表1所列为模型的工艺参数和特性参数。
3.2 模拟结果与分析
3.2.1 不同拉速下铸坯的温度分布
图2所示分别为不同拉速下的温度分布图, 采用渐变色表示温度变化。
图3所示分别为不同拉速下的温度分布曲线。
表1 工艺参数和物性参数表
Table 1 Technological parameters and physical parameters
图2 不同拉速下的温度分布
Fig.2 Temperature distribution at different casting speeds
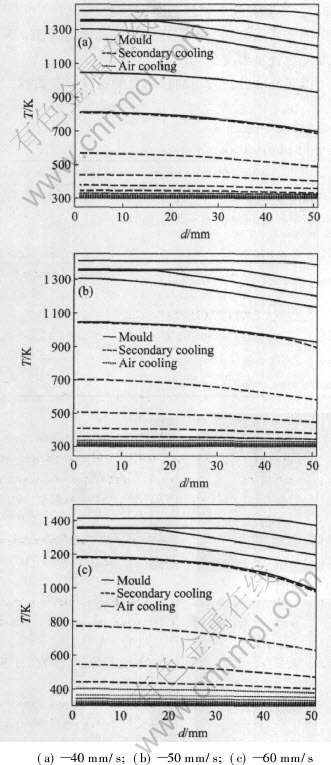
图3 不同拉速下的温度分布曲线
Fig.3 Temperature distribution at different casting speeds
由图2和图3可以看出, 在一定的连铸工艺条件下, 随着拉速的提高, 出坯温度明显升高。 因此为了防止拉漏, 在其他工艺条件不变的情况下, 应合理选择拉坯速率。
3.2.2 不同冷却条件下铸坯的温度分布
表2、 3和4所列为拉速50mm/s时, 不同冷却条件(经验常数B)下铸坯的温度分布情况。 如上文所述, 经验常数B与水流量W以及结晶器进出水温差ΔTw等冷却条件参数密切相关。
表2 B=2.02×104时铸坯中心及表面温度
Table 2 Centre temperature and surface temperature at different measure positions and B=2.02×104
表3 B=3.02×104时铸坯中心及表面温度
Table 3 Centre temperature and surface temperature at different measure positions and B=3.02×104
表4 B=4.02×104时铸坯中心及表面温度
Table 4 Centre temperature and surface temperature at different measure positions and B=4.02×104
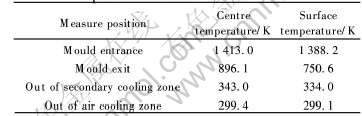
由表2、 3和4可以看出, 随着经验常数B的增大, 铸坯中心温度及表面温度逐渐降低。 经验常数B对出结晶器区温度的影响尤为突出, 随着B值的增大, 温度呈显著降低的趋势。 这是由于B是W和ΔTw的函数, 而W和ΔTw的取值反映了结晶器区的冷却条件。
3.3 模型的验证
为了验证模型的准确性, 在生产中, 采用远红外测温仪进行不同点的温度测试。 表5所列为当B=2.02×104, 拉速为60mm/s时, 铸坯中心及表面温度模拟计算结果与实验结果的比较。
从表5可以看出, 总的来说, 铸坯表面温度的实验值比计算值偏低, 这可能是由于铸坯表面不是理想光滑所致。 计算值与实验值大约相差0~7℃, 在误差允许范围内, 这表明模拟计算结果真实可靠。
表5 铸坯中心及表面温度计算值与实验值的比较
Table 5 Comparison of values of calculated centre temperature and surface temperature with measured ones
REFERENCES
[1]Yamanaka A, Kumakura S, Okamura K, et al. Thin slab casting with liquid core reduction [J]. Ironmaking and Steelmaking, 1999, 26(6): 457-462.
[2]时义祥, 何绪友, 王爱霞, 等. 薄板坯连铸连轧的发展现状及应用探讨[J]. 山东冶金, 2003, 25(2): 1-3.
SHI Yi-xiang, HE Xu-you, WANG Ai-xia, et al. Discussion on current status and application of thin slab continuous casting and rolling [J]. Shandong Metallurgy, 2003, 25(2): 1-3.
[3]丁培道, 蒋斌, 杨春楣, 等. 薄带连铸技术的发展现状与思考[J]. 中国有色金属学报, 2004, 14(1): 192-196.
DING Pei-dao, JIANG Bin, YANG Chun-mei, et al. Development and thought of thin-strip continuous casting [J]. The Chinese Journal of Nonferrous Metals, 2004, 14(1): 192-196.
[4]张炯明, 张力, 王新华, 等. 板坯连铸结晶器热流量分布的研究[J]. 金属学报, 2003, 39(12): 1285-1290.
ZHANG Jiong-ming, ZHANG Li, WANG Xin-hua, et al. Study of heat flux distribution in continuous casting mold [J]. Acta Metallurgica Sinica, 2003, 39(12): 1285-1290.
[5]崔立新, 张家泉, 陈素琼, 等. 连铸板坯在结晶器内凝固行为的研究[J]. 炼钢, 2003, 19(3): 22-25.
CUI Li-xin, ZHANG Jia-quan, CHEN Su-qiong, et al. Research on solidification of continuous casting slab in mould[J]. Steel Making, 2003, 19(3): 22-25.
[6]张富强, 王军, 梁祥远. 中薄板坯高拉速连铸结晶器平均热流研究[J]. 钢铁, 2002, 37(12): 19-20.
ZHANG Fu-qiang, WANG Jun, LIANG Xiang-yuan. Study on average heat flux in mold of medium thin slab caster[J]. Iron and Steel, 2002, 37(12): 19-20.
[7]Thomas G O, Jonathan A D. Modeling the thin-slab continuous casting mould [J].Metall Trans B, 1994, 25: 443-458.
[8]Dvorkin E N. Finite element models in the steel industry Part Ⅰ: Simulation of flat product manufacturing processes [J]. Computer and Structures, 2003, 81: 559-573.
[9]杨建伟, 杜艳平, 史荣, 等. 异形坯连铸结晶器内三维流场的数值模拟[J]. 中国有色金属学报, 2001, 11(2): 248-252.
YANG Jian-wei, DU Yan-ping, SHI Rong, et al. 3D numerical simulation on flowing distribution in mould for beam blank continuous casting [J]. The Chinese Journal of Nonferrous Metals, 2001, 11(2): 248-252.
[10]Lser W, Thiem S, Jurisch M. Solidification modeling of microstructures in near-net-shape casting of steels [J]. Mater Sci Eng A, 1993, 173(1-2): 323-326. 2001, 11(2): 248-252.
[11]Wiwatanapataphee B, Wu Y H, Archapitak J, et al. A numerical study of the turbulent flow of molten steel in a domain with a phase-change boundary [J]. Journal of Computational and Applied Mathematics, 2004, 166: 307-319.
[12]Seyedein S H, Hasan M. A three-dimensional simulation of coupled turbulent flow and macroscopic solidification heat transfer for continuous slab casters [J]. Int J Heat Mass Transfer, 1997, 40(18): 4405-4423.
[13]Shi Z, Guo Z X. Numerical heat transfer modeling for wire casting [J]. Mater Sci Eng A, 2004, 365(1-2): 311-317.
[14]Lally B, Biegler L, Henein H. Finite difference heat-transfer modeling for continuous casting [J]. Metall Trans B, 1990, 21: 716-720.
[15]高家锐. 动量、 热量、 质量传输原理[M]. 重庆: 重庆大学出版社, 1987. 167-171.
GAO Jia-rui. Momentum, Heat and Mass Transfer Theory [M]. Chongqing: Chongqing University Press, 1987. 167-171.
[16]杨全. 金属凝固与铸造过程数值模拟[M]. 杭州: 浙江大学出版社, 1996. 26-31.
YANG Quan. Numerical Simulation of the Solidification of Metals and Casting Process [M]. Hangzhou: Zhejiang University Press, 1996. 26-31.
[17]Wind J S, et al. Solution for the solidification problem of one-dimensional medium by a new numerical method [J]. Journal of Iron and Steel Institute, 1963, 201(7): 594-601.
[18]贺友多. 传输过程的数值方法[M]. 北京: 冶金工业出版社, 1991. 131-132.
HE You-duo. Numerical Methods of Transport Process [M]. Beijing: Metallurgical Industry Press, 1991. 131-132.
(编辑何学锋)
收稿日期: 2004-08-09; 修订日期: 2005-01-02
作者简介: 李金山(1967-), 男, 教授, 博士.
通讯作者: 李金山, 教授; 电话: 029-88491074; E-mail: ljsh@nwpu.edu.cn
