
J. Cent. South Univ. (2019) 26: 3351-3358
DOI: https://doi.org/10.1007/s11771-019-4258-5
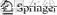
DCS devices based non-linear process control system design for plants with distributed time-delay using particle filter
DENG Ming-cong(邓明聪), FUJII Ryohei(藤井涼平)
The Graduate School of Engineering, Tokyo University of Agriculture and Technology,Tokyo 184-8588, Japan
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Abstract: Remote control process system with distributed time-delay has attracted much attention in different fields. In this paper, non-linear remote control of a single tank process system with wireless network is considered. To deal with the distributed time-delay in a large-scale plant, the time-delay compensation controller based on DCS devices is designed by using operator theory and particle filter. Distributed control system (DCS) device is developed to monitor and control from the central monitoring room to each process. The particle filter is a probabilistic method to estimate unobservable information from observable information. First, remote control system and experimental equipment are introduced. Second, control system based on an operator theory is designed. Then, process system with distributed time-delay using particle filter is carried out. Finally, the actual experiment is conducted by using the proposed time-delay compensation controller. When estimating with the proposed method, the result is close to the case in which the distributed time-delay does not exist. The effectiveness of the proposed control system is confirmed by experiment results.
Key words: non-linear remote control; distributed control system; particle filter; operator theory; distributed time-delay
Cite this article as: DENG Ming-cong, FUJII Ryohei. DCS devices based non-linear process control system design for plants with distributed time-delay using particle filter [J]. Journal of Central South University, 2019, 26(12): 3351-3358. DOI: https://doi.org/10.1007/s11771-019-4258-5.
1 Introduction
In chemical plants and petroleum plants, the temperature, flow rate and liquid level of various processes are controlled to stability and efficiency [1]. In general, there are multiple processes in the large-scale plant since a plurality of sensors and actuators are installed for each process to control. This process equipment is monitored and controlled from the central monitoring room to each process. Distributed control system (DCS) device is developed to satisfy these demands [2]. Recently, the movement of wireless communication of sensors has emerged, as well as remote control between field control station (FCS) and field equipments using wireless communication. The advantages of DCS devices by wireless communication are the reduction of wiring costs and the extension of facilities. However, in practical tank process systems, the distributed time-delays are inherent features and are often the main cause for instability and poor performance. The stability of an equilibrium may be lost when delays are increased. In this study, the distributed time-delay is formulated by the integral of the output. DCS devices by wireless communication are necessary to take time-delays inherent in the remote control system into consideration [3]. Thus, the distributed time-delay must be compensated. Moreover, the compensation for DCS devices with distributed time-delay process system was also discussed in previous work [4-6]. The particle filter is a probabilistic method to estimate unobservable information from the observable information. Thus, the particle filter which is applied to the control system has the distributed output time-delay [7-9]. Operator based non-linear feedback control systems have been also discussed for non-linear analysis, design, stabilization, and control in different fields [10-13].
In this paper, we aim to propose a control system design to suppress deterioration of control performance due to communication delay. Distributed time-delay is considered when process equipment is controlled by a wireless network in a large-scale plant. To prevent a decline of a control performance by the time-delay, the time-delay compensation controller is designed using operator theory and particle filter. Besides, the experimental environment which simulates the DCS devices is made, and the effectiveness of the designed control system is confirmed by experiment results.
The rest paper is organized as follows. In Section 2, remote control system and experimental equipment are reviewed to develop main results of the paper and the problem statements are set up. In Section 3, distributed time-delay control system design using particle filter is conducted. In Section 4, experimental results are given to confirm the effectiveness of the proposed design scheme. Conclusions of this paper are drawn in Section 5.
2 Problem
In this section, remote control system and experimental equipment are recalled for developing the main results of this paper and then the problem statements are set up.
2.1 Remote control system
The remote control system with distributed time-delay, which is considered in this paper, is denoted in Figure 1. In a large-scale plant, a remote control system includes a remote control unit and a controlled unit. The remote control unit is moved in space, and includes a movement detector, selection switch and transmitter. The movement detector detects movement of the remote control unit. The transmitter transmits output of the movement detector and the selection switch. The controlled unit includes of which a display device, receiver, and controller. The controller moves the cursor across the display screen in accordance with the output of the movement detector and the selection switch [2]. However, all wireless modules cannot work simultaneously due to the limit of radio channel. Thus, the time-delay occurs with control input from the central monitoring room to a process equipment and sensor output from t process equipment to the central monitoring room. A decline of control performance due to the time- delay is concerned. In this paper, the compensation of the time-delay is mainly conducted.
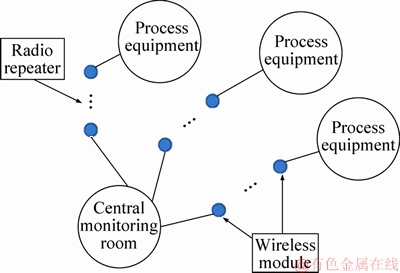
Figure 1 Wireless communication control system in large-scale plant
2.2 Experimental equipment
The configuration of the experimental system handled in this research is shown in Figure 2. DCS device takes on a role of the central monitoring room. In the personal computer, the sensor signal of the process is fed back via the PCI board (Interface Corporation, PCI-3521), and the control input is calculated, and the value is handled. Here, since the electrical signal handled by the personal computer is a voltage of 0-5 V and current handled by the process device is 4-20 mA, there is a signal conversion circuit between the personal computer and the process device. The signal converted from voltage to current is sent to the process by the signal conversion circuit. Distributed time-delay is generated in the interior of PC. Therefore, this research aims to compensate for the bad effect on the control system due to network time-delay.
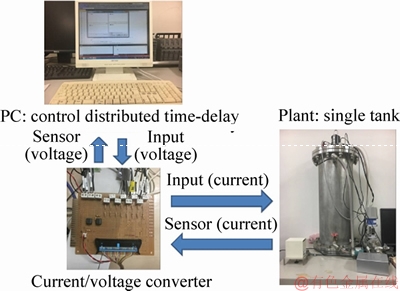
Figure 2 Experimental equipment
In this experimental setup, the control experiment of the liquid level of the tank 1 can be performed. The liquid is pumped up from the tank 3 to the upper part of the tank 1 by the pump (P1) and the liquid flows out from the lower part of the tank 1 and returns to the tank 3. The water level in the tank can be kept at the desired water level or constant by adjusting the motorized valve and the influent of which the outflow rate is controlled by the electric valve. Block diagram of experimental equipment is shown in Figure 3.
Figure 3 Block diagram of experimental equipment
2.3 Problem statement
In this paper, the control system in the case where distributed time-delay occurs in the output of process system is proposed. The output distributed time-delay is Φ, and the output y'(t) influenced by the distributed time-delay is expressed as follows:
 (1)
(1)
where y(t) is the output before being influenced by the distributed time-delay; Td is the upper limit of the integration of which the upper limit of the communication delay generates at the output. When a normal feedback control system is configured for a process with distributed time-delay, the distributed time-delay has a bad influence on the feedback control system, and it leads to depress the performance of control. In this paper, the distributed time-delay compensation controller is designed by using operator theory and particle filter to improve performance of the control system with time-delay.
3 Distributed time-delay control design using particle filter
In this section, a control system based on an operator theory is designed. Particle filter is carried out for process system with distributed time-delay.
3.1 Control system design based on operator theory
In this work, the design of control system is based on operator theory. Appendix A gives additional information to explain some definitions and notations about operator theory in detail. In operator theory, the controlled object P is regarded as the mapping from input u to output y, where y=P(u). This mapping P is a non-linear model of input-output relation of the controlled object. Plant P satisfies a right factorization if there are two stable operators N and D-1. Moreover, plant P is said to have a right coprime factorization if there are two stable operators S and R, which satisfy the Bezout identity SN+RD=I, where I is an identity operator, and u=I(y)=y. The closed-loop system is illustrated in Figure 4.
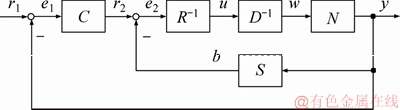
Figure 4 Stability and tracking performance based on operator theory
Based on the procedure of the operator theory described above, P has a right factorization on operators N and D-1, and operators S and R-1 are designed to satisfy the Bezout identity. Operators N, D-1, S and R-1 are given as follows:
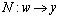
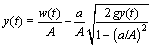 (2)
(2)
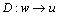
u(t)=w(t) (3)
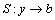
 (4)
(4)
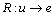
e(t)=Ku(t) (5)
where w(t) is width of flow channel; A and a are the cross-sectional area and the outflow cross-sectional area of tank, respectively; g is the gravitational acceleration; K is a designed parameter.
The controller C is represented by the following equation:
C: e 1 → r2
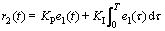 (6)
(6)
Here KP and KI are the proportional gain and the integral gain, respectively.
3.2 Closed-loop system with time-delay
In this subsection, the time-varying delay occurs with input-output of process equipment due to the remote control by using a network. Therefore, the influence of the time-delay with input-output is represented by operators Φ1 and Φ2 in Figure 5. Operators Φ1 and Φ2 are given in Eqs. (7) and (8).
 (7)
(7)
 (8)
(8)

Figure 5 Closed loop system based on an operator theory with input-output time-delay
3.3 Distributed time-delay control system design using particle filter
In remote control system, the present output value is estimated from the feedback output value influenced by distributed time-delay. To compensate for the influence of distributed time-delay, the control system is using a particle filter [14, 15], which is the estimating mechanism. Block diagram of the proposed control system is shown in Figure 6.
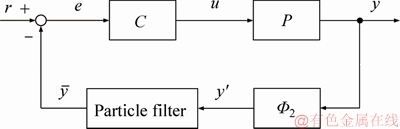
Figure 6 Block diagram of proposed control system
The proposed distributed time-delay control system design is shown in Figure 7. Here, N and D-1 are operators who decompose the plant to the right; S and R-1 are stabilized and designed to satisfy the Bezout identity SN+RD=I; Φ2 is the operator which is denoted the distributed time-delay of the output. The particle filter is a probabilistic method to estimate unobservable information from observable one. Basic theory of particle filter algorithm is given by Appendix B in detail. Thus, the particle filter can be applied to the distributed control system with the output time-delay.

Figure 7 Proposed distributed time-delay control system design
4 Experimental result
In this section, the effectiveness of the distributed time-delay compensation control system using the particle filter was verified by actual experiments, and the parameters are shown in Table 1. According to the Bezout identity, the experimental parameters S and R-1are set up. KP and KI are the proportional gain and the integral gain, respectively.
4.1 Process system without distributed time- delay
In this subsection, we conducted an actual experiment in the case where the distributed time-delay does not occur in the output. The results are shown in Figures 8 and 9. In this case, there is no distributed time-delay in the output, so normal follow-up control is possible. It is understood that it follows the target water level in about 80 s from the beginning of control. The proposed method was evaluated by the actual machine experiment.
Table 1 Experimental parameters

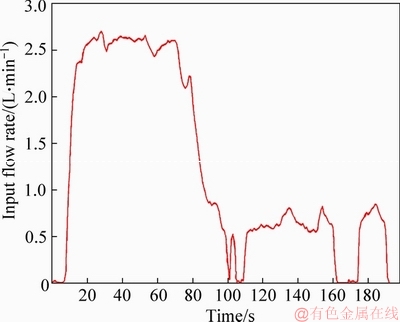
Figure 8 Input of experiment without delay
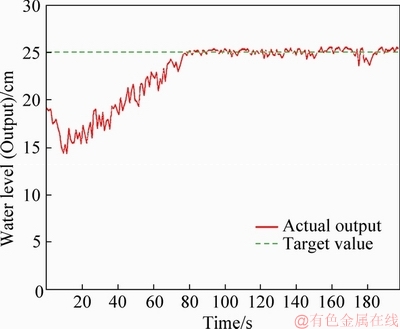
Figure 9 Output of experiment without delay
4.2 Proposed compensation controller for process system with distributed time-delay
Figures 10 and 11 show the results of the experiment using the proposed method when the distributed time-delay is generated in the output.In this case, the initial water level is 17.39 cm.As can be seen from the results in Figure 11, the result is close to that in the case where the distributed time-delay does not exist. It is about 80 s within the range of ±1 cm, which is an error between the actual output value and the estimated value. Therefore, it is verified that the proposed control system is effective against the distributed time-delay generated at the output.
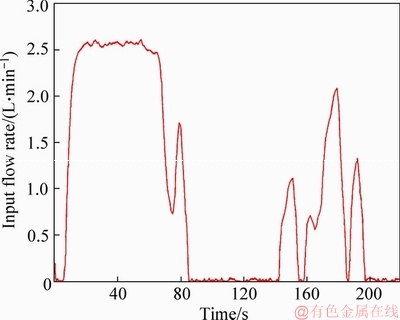
Figure 10 Input of experiment with proposed method
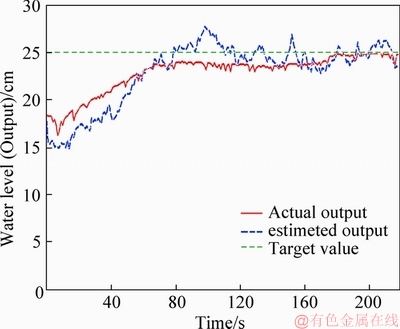
Figure 11 Output of experiment with proposed method
5 Conclusions
In this paper, the time-delay compensation controller is designed by using operator theory and particle filter for non-linear remote control system with the distributed time-delay. The compensation controller with distributed time-delay is used particle filter algorithm. The effectiveness of the proposed method is confirmed by two compassion experiments. In fact, dealing with the design of the tracking filter C, we can select the parameters of C by using the ant colony optimization [16-18], so that optimal controller parameters can be obtained.
Appendix
A Operator theory
Definition 1: Let U and Y be linear spaces over the field of complex numbers, and the normed linear subspaces Us and Ys are also called the stable subspaces of linear spaces U and Y, respectively. Let A: U→Y be an operator. For any defined operator, they are causal, but not necessarily linear or bounded (with a finite operator norm). We always assume that D(Q)=U with R(Q) Y. In this note, an operator Q: U→Y is said to be bounded input bounded output (BIBO) stable or simply stable if Q(Us)
Y. In this note, an operator Q: U→Y is said to be bounded input bounded output (BIBO) stable or simply stable if Q(Us) Ys.
Ys.
Definition 2: Let (U, Y) be the set of stable operators from U to Y. Then(U, Y) contains such a subset defined by u(U, Y)={M:M∈(U, Y), where M is invertible with M-1∈(Y, U)}, and elements of (U, Y) are called unimodular operators.
Definition 3: Let F be the family of real-valued measurable functions defined on [0,∞), which is a linear space. For each constant T∈[0, ∞), let PT be the projection operator mapping from F to another linear space FT, of measurable functions such that
fT(t):=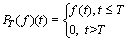
where fT(t)∈FT is called the truncation of f(t) with respect to T. Then, for any given Banach space XB of easurable functions, where a Banach space is a complete vector space with a norm, set
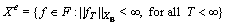
where XB is a linear subspace of F. The defined space is called the extended linear space associated with the Banach space XB.
Definition 4: Let Ue and Ye be two extended linear spaces, which are associated respectively with two given Banach spaces UB and YB of measurable functions defined on the time domain [0, ∞). Let De be a subset of Ue, a non-linear operator A: De→Ye is called a generalized Lipschitz operator on De if there is a constant L such that
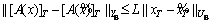
for all x,  and for all T∈[0, ∞). Lip (De) denotes the family of non-linear generalized Lipschitz operators that map De to itself. Note that the least such constant L is given by
and for all T∈[0, ∞). Lip (De) denotes the family of non-linear generalized Lipschitz operators that map De to itself. Note that the least such constant L is given by
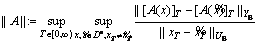
Supposing that the system shown in Figure A1 is well-posed, if the unstable plant has a right coprime factorization, and the Bezout identity is
SN+RD=M
there is satisfied feedback, where M, S and R-1 represent the unimodular operator, and feedforward controllers, respectively, then the system is overall stable [10, 12]. Therefore, the non-linear feedback system shown in Figure A1 can be equivalently transformed as the system shown in Figure A2, then we can find that the plant output tracks to the reference output by satisfying:
NM-1 = I

Figure A1 Non-linear feedback system

Figure A2 Equivalent system
B Particle filter
The particle filter algorithm used in the proposed control system will be explained in detail [7, 8]. Schematic of particle filter is shown in Figure B1.
Let xt be unobservable state variable and ytbe the observed value at time t. The system model f(·) and the observation model h(·) are given as follows:
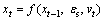 ;
;
 ∈t)
∈t)
where εs and εm are parameters of the system model and observation model, respectively; vtand ∈tare system noise and observation noise which are generated by the Monte Carlo method, respectively.
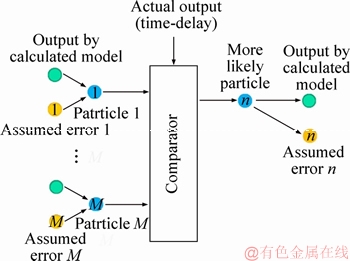
Figure B1 Schematic of particle filter
According to the standard algorithm of the particle filteras follows:
1) Particle set initialization, k=0:
As for i=1, 2, …, M, the sampled particles  are generated from prior probability p(x0).
are generated from prior probability p(x0).
As for k=1, 2, …, cycle through the following steps:
Important sampling: As for i=1, 2, …, M, the sampled particles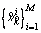 are generated from importance probability density, and then calculate particle weights
are generated from importance probability density, and then calculate particle weights 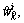 and normalize
and normalize 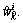
Resampling: replace unlikely samples with more likely ones. After resampling the particle set 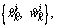 the particle set is
the particle set is 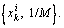
Calculate the state estimate at the time k, .
.
The prior probability distribution is approximated by:
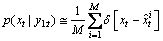
where the number of particles is M, after resampling particles 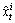 , i={1, 2, …, M}.
, i={1, 2, …, M}.
Acknowledgment
The authors would like to thank Miss LI Xi-mei at Tokyo University of Agriculture and Technology, Japan, for her suggestions and comments.
References
[1] STEFFEN W. Process control in the chemical industry [D]. Chemical Engineering Department, King Saud University, 2002: 132-145.
[2] FUJII R, DENG Ming-cong, WAKITANI S. Nonlinear remote temperature control of a spiral plate heat exchanger [C]// 2015 International Conference on Advanced Mechatronic Systems (ICAMechS). New York, USA: IEEE, 2015: 533-537.
[3] DENG Ming-cong, INOUE A. Networked non-linear control for an aluminum plate thermal process with time-delays [J]. International Journal of Systems Science, 2008, 39(11): 1075-1080.
[4] WANG Ai-hui, DENG Ming-cong. Operator-based robust nonlinear tracking control for a human multi-joint arm-like manipulator with unknown time-varying delays [J]. Applied Mathematics & Information Sciences, 2012, 6(3): 459-468.
[5] MICHIELS W, MORARESCU C I, NICULESCU S I. Consensus problems with distributed delays, with application to traffic flow models [J]. SIAM Journal on Control and Optimization, 2009, 48(1): 77-101.
[6] WEN Sheng-jun, DENG Ming-cong, BI Shu-hui, WANG Dong-yun. Operator-based robust nonlinear control and its realization for a multi-tank process by using a distributed control system [J]. Transactions of the Institute of Measurement and Control, 2012, 34(7): 891-902.
[7] MERWE R V D, DOUCET A, FREITAS N D, WAN E. The unscented particle filter [J]. Advances in Neural Information Processing Systems, 2001(13): 584-590.
[8] YANG Tao, LAUGESEN R S, MEHTA P G, MEYN S P, Multivariable feedback particle filter [J]. Automatica, 2016, 71: 10-23.
[9] CHEN Zeng-qiang, WU Xia, SUN Ming-wei, SUN Qing-lin. Performance analysis of active disturbance rejection generalized predictive control on time-delay systems [J]. Journal of Central South University: Science and Technology, 2018, 49(8): 1960-1970. (in Chinese)
[10] DENG M, INOUE A, ISHIKAWA K. Operator-based nonlinear feedback control design using robust right coprime factorization [J]. IEEE Transactions on Automatic Control, 2006, 51(4): 645-648.
[11] WEN Sheng-jun, DENG Ming-cong. Operator-based robust nonlinear control and fault detection for a Peltier actuated thermal process [J]. Mathematical and Computer Modelling, 2013, 57(1, 2): 16-29.
[12] DENG Ming-cong. Operator-based nonlinear control systems [M]. Hoboken, NJ, USA: John Wiley & Sons, Inc., 2014.
[13] DENG Ming-cong, JIANG Chan-gan, INOUE A, SU Chun-yi. Operator-based robust control for nonlinear systems with Prandtl-Ishlinskii hysteresis [J]. International Journal of Systems Science, 2011, 42(4): 643-652.
[14] ZHANG Tie, MA Qiong. Target location and tracking based on local background feature points [J]. Journal of Central South University: Science and Technology, 2016, 47(9): 3040-3049. (in Chinese)
[15] HU Xiu-hua, GUO Lei, LI Hui-hui, YAN Pan-deng. New method for joint detection and tracking with variable maneuvering target number [J]. Journal of Central South University: Science and Technology, 2016, 47(10): 3424-3435. (in Chinese)
[16] YANG Qiang, CHEN Wei-neng, YU Zheng-tao, GU Tian-long, LI Yun, ZHANG Hua-xiang, ZHANG Jun. Adaptive multimodal continuous ant colony optimization [J]. IEEE Transactions on Evolutionary Computation, 2017, 21(2): 191-205.
[17] CHEN Zong-gan, ZHAN Zhi-hui, LIN Ying, GONG Yue-jiao, GU Tian-long, ZHAO Feng, YUAN Hua-qiang, CHEN Xiao-feng, LI Qing, ZHANG Jun. Multiobjective cloud workflow scheduling: A multiple populations ant colony system approach [J]. IEEE Transactions on Cybernetics, 2019, 49(8): 2912-2926.
[18] GONG Yue-jiao, CHEN En, ZHANG Xing-lin, NI L M, ZHANG Jun. AntMapper: An ant colony-based map matching approach for trajectory-based applications [J]. IEEE Transactions on Intelligent Transportation Systems, 2018, 19(2): 390-401.
(Edited by ZHENG Yu-tong)
中文导读
基于粒子滤波的分布式时滞过程系统的分散控制器
摘要:具有分布式时滞的远程控制处理系统在不同领域备受关注。本文考虑了具有无线网络的单水箱处理系统的非线性远程控制。为了解决大型工厂的分布式时滞问题,采用算子理论和粒子滤波设计了基于DCS器件的延时补偿控制器。分散控制系统(DCS)设备以从中央监控室到每个过程进行监控和控制。粒子滤波是一种概率方法,用于从可观测的信息中估计不可观测的信息。首先,介绍了远程控制系统和实验设备。其次,设计了基于算子理论的控制系统。接着,使用粒子滤波执行具有分布式时滞的处理系统。最后,通过使用所提出的时滞补偿控制器进行实验。通过所提出的方法进行估计,结果接近于不存在分布式时间延迟的情况。实验结果证实了所提出的控制系统的有效性。
关键词:非线性远程控制;分散控制系统;粒子滤波;算子理论;分布型时滞
Foundation item: Project(K117K06225) supported by JSPS KAKENHI, Japan
Received date: 2018-11-01; Accepted date: 2019-06-10
Corresponding author: DENG Ming-cong, PhD, Professor; Tel: +81-42-388-7134; E-mail: deng@cc.tuat.ac.jp; ORCID: 0000-0001- 7411-6602