文章编号:1004-0609(2010)S1-s0352-05
Ti-Zr二元体系BCC相扩散移动性的评估
陈 逸1,钟 宏1,唐 斌1,崔予文2,李金山1,常 辉1,周 廉1
(1. 西北工业大学 凝固技术国家重点实验室,西安 710072;
2. 美国俄亥俄州立大学 材料科学与工程学院,哥伦布市 43210)
摘 要:在丰富实验数据的基础上,结合相关的热力学参数,评估并获得Ti-Zr二元体系BCC相中的扩散移动性数据库。通过扩散移动性数据库计算的扩散系数与实验数据取得很好的一致性。基于Calphad技术,在所获得的扩散移动性数据库的基础上,结合相关的热力学描述,成功地模拟Ti-Zr二元体系半无限扩散偶浓度曲线和Kirkendall面的移动,并计算点阵面的移动距离。
关键词: Ti-Zr二元体系;扩散;Calphad;Dictra模型
中图分类号:TG111.6 文献标志码:A
Assessment of diffusional mobilities of BCC phase in Ti-Zr alloys
CHEN Yi1, ZHONG Hong1, TANG Bing1, CUI Yu-wen2, LI Jin-shan1, CHANG Hui1, ZHOU Lian1
(1. State Key Laboratory of Solidification Processing, Northwestern Polytechnical University, Xi’an 710072, China;
2. Department of Materials Science and Engineering, The Ohio State University, Columbus, OH 43210, USA)
Abstract: Based on the thermodynamic parameters and various experimental diffusion data available in the literature, the atomic mobilities for BCC phase of the Ti-Zr binary system were evaluated. The general agreement is obtained by comprehensive comparisons made between the calculated and experimental diffusion coefficients. The developed mobility database, in conjunction with the CALPHAD-type thermodynamic description, is successfully used to simulate the concentration profiles, such as typical experimental interdiffusion phenomena and the microstructural stability of the Kirkendall plane, and the lattice plane displacement was calculated.
Key words: Ti-Zr binary system; diffusion; Calphad; Dictra–modeling
钛合金由于具有密度低、强度高、耐腐蚀和高温性能好等优点,在航空、航天和石化等领域得到越来越广泛的应用[1]。合金中的许多热处理工艺、强化机制以及绝大多数的相转变取决与复杂的扩散过程。对扩散过程的分析和模拟可以为预测先进材料的相关性能提供帮助。锆是钛合金的一种重要的合金元素,是高强钛合金、耐蚀钛合金、高温钛合金和低温钛合金的一种常用元素。研究Ti-Zr二元体系的扩散可以为研究钛合金多元体系扩散提供基础,进而为研究钛合金热处理工艺和强化机制等提供依据。
计算机模拟是一种成本极低、有效的研究二元体系扩散控制过程的方法。Calphad(Calculation of phase diagram)技术为我们提供一个研究扩散移动性的思 路[2]。在丰富实验数据的基础上,结合相关的热力学参数,可以评估并获得一个体系的扩散移动性参数。并进一步在所获得的扩散移动性参数的基础上,结合以Calphad为基础的热力学描述,可以预测更深层次的扩散行为,如半无限扩散偶浓度曲线、Kirkendall面微观组织的稳定性以及点阵面的移动等。
因此,本研究的目的首先在于评估并获得精确的Ti-Zr二元体系BCC相中的扩散移动性参数,以及完善的Ti基扩散移动性数据库。其次,通过模拟深层次的扩散行为来更好的理解其扩散特性。
1 扩散原子移动性模型
根据绝对反应速率理论,组元B的移动系数(MB)可以被分成两部分,一部分是频率因子(MB0),另一部分是激活焓QB:
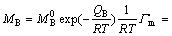
 (1)
(1)
式中:Γm是考虑磁效应的因子,它与合金成分有关;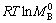 和QB即为所要优化的移动性参数,用Qi表示,它依赖于组分、温度以及压力的变化。根据CALPHAD方法,Qi可以用Redlich-Kister展开:
和QB即为所要优化的移动性参数,用Qi表示,它依赖于组分、温度以及压力的变化。根据CALPHAD方法,Qi可以用Redlich-Kister展开:
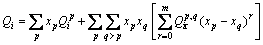 (2)
(2)
式中:xp是组元p的摩尔分数;Qip是纯组元i的Qi,所以它代表成分空间的一个边界值;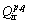 是二元相互作用参数。Qip和
是二元相互作用参数。Qip和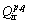 可以通过评估实验数据获得。
可以通过评估实验数据获得。
2 扩散移动性的评估
扩散移动性的评估是建立在获得其热力学描述的基础上的。对于Ti-Zr二元体系,KUMAR等[3]已经给出Ti-Zr二元体系的热力学模型,并评估其热力学参数。本文作者主要使用DICTRA软件中的Parrot模块来进行优化,其原理是运用最小二乘法来拟合实验参数。对于Ti-Zr二元体系BCC相,需要优化的参数有纯组元原子扩散移动性参数以及二元相互作用参数。表1所列为最终获得的扩散移动性参数。
2.1 示踪扩散系数
Ti在β-Ti中的的自扩散以及Zr在β-Zr中的的自扩散由于经过多晶型转变,呈现出不规则的扩散特性,如非线性的Arrhenius曲线、较低的频率因子和激活能。在DICTRA软件中,需要使用更复杂的模型来处理这种反常扩散问题。比如采用线性方程拟合,也可以采用分段线性函数或者是D=D1exp[-Q1/(RT)]+ D2exp[-Q2/(RT)]。采用第一种策略能较好地反映出曲线特性。但它不能区分激活能和频率因子相,也就是说它的物理意义不明显。同时,如果体系有磁性相存在,则不能使用第一种策略。选用第二种策略可以将误差值限定在可以接受的范围内,并且能直接运用到扩散移动性数据库中。它的缺点是不能明显的反映出曲线的特性并且物理意义不明显。选用第三种策略能同时反映出曲线的特性以及有明确的物理意义,但是模型比较复杂。
CHEN[4]和LIU等[5]分别评估Ti在β-Ti中的的自扩散。LIU等[5]采用第一种策略评估Ti在β-Ti中的的自扩散,CHEN[4]采用第三种策略评估了Ti在β-Ti中的的自扩散。图1所示为计算得到的Ti在β-Ti中的自扩散系数的对数值与温度倒数的关系曲线,并且给出了计算值与实验值[6-9]的比较。图中的虚线为LIU等[5]所计算的结果,由此可以看出误差较大,因此本文作者采用了CHEN所获得的Ti在β-Ti中的扩散移动性参数。图2所示为所计算的Zr在β-Zr中的自扩散系数与LUNDY[10]和PATIL[11]得到的实验值的比较。虚线是LIU等[5]所计算的结果,采用分段函数进行拟合,虽然能较好地反应出曲线的特性,但曲线的物理意义不明显。
表1 Ti-Zr二元体系BCC相的扩散移动性参数
Table 1 Mobility parameters for BCC phase in Ti-Zr binary system
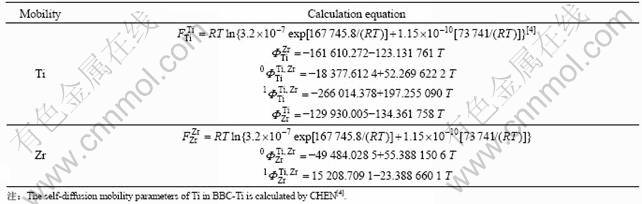
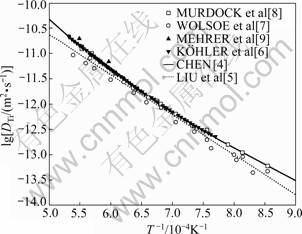
图1 Ti在β-Ti中的自扩散系数
Fig.1 Free diffusion coefficient of Ti in β-Ti
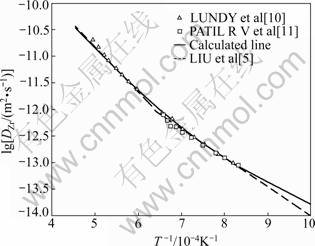
图2 Zr在β-Zr中的自扩散系数
Fig.2 Free diffusion coefficient of Zr in β-Zr
图3所示为所计算的Ti在β-Zr中的杂质扩散系数与ZEE等[12]和RAGHUNATHAN等[13]所获得的实验值的比较。由图3可以看出,计算值能较好地符合实验值。图4所示为运用DICTRA软件所计算的Zr在β-Ti中的杂质扩散系数的对数值与温度倒数的关系曲线。由图4可以看出,所获得的结果能较好的符合ARAKI等[14]的实验结果。
2.2 相互扩散系数
在获得上述扩散移动性数据的基础上,本文作者可以得到Ti-Zr相互扩散的移动性数据。图5对比了计算得到的相互扩散系数与THIBON[15]获得的实验数据。由图5可以看出,优化结果能较好的符合实验数据。由图可以得出以下结论:Ti-Zr二元体系BCC相BCC相的相互扩散系数随成分(Zr的浓度范围在20%~80%时)的变化不大,但在两端的变化很明显。
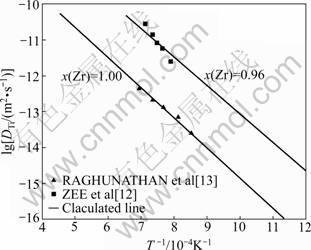
图3 Ti在β-Zr中的杂质扩散系数
Fig.3 Impurity diffusion coefficients of Ti in β-Zr
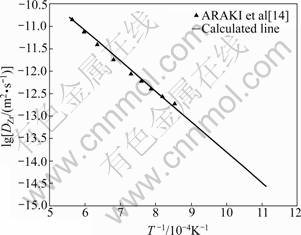
图4 Zr在β-Ti中的杂质扩散系数
Fig.4 Impurity diffusion coefficients of Zr in β-Ti
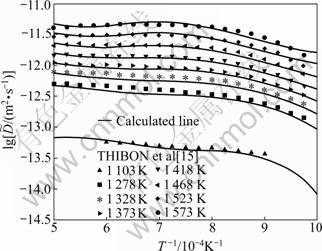
图5 Ti-Zr体系BCC相相互扩散系数的计算值与THIBON[15]获得的实验值的比较
Fig.5 Comparison between calculated and experimentally values obtained by THIBON of interdiffusion coefficients of BCC phase in Ti-Zr system
3 扩散模拟
对获得的扩散参数可靠性的确认不仅仅是与实验获得的扩散系数做比较,同时,需要通过相互扩散来模拟一些更深程度的扩散行为,并与实验进行比较。在已评估的移动性参数的基础上,结合以CALPHAD为基础的热力学可以模拟扩散偶实验中的许多扩散现象。
3.1 Ti-Zr扩散偶的浓度曲线
为了能更好地检验所获得的扩散移动性数据的准确性,需要计算Ti-Zr二元扩散偶的浓度曲线,并与实验数据进行比较。图6所示为计算得到的浓度曲线,其中Ti-Zr扩散偶的扩散退火温度T=1 673 K,时间t= 3 720 s。由图6可以看出,计算值与实验值符合的很好。这进一步证明了所获得的移动性参数的准确性。
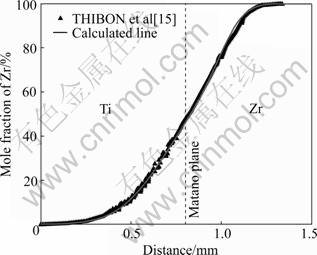
图6 Ti-Zr扩散偶浓度曲线的计算值与实验值的对比
Fig.6 Comparison between calculated and experimentally values measured interdiffusion concentration pro?le
3.2 Ti-Zr体系Kirkendall面的移动
惰性标记面的移动速度取决与组元的本征扩散系数以及扩散区域浓度梯度的变化。图7所示为两种本征扩散系数DTi与DZr随浓度的变化曲线。其DI为Ti在Ti-Zr二元体系中的本征扩散系数;DII为Zr在Ti-Zr二元体系中的本征扩散系数;DC为Ti-Zr二元体系的的扩散系数。由图7中可以看出,在Matano面附近,Ti的本征扩散系数大于Zr的本征扩散系数,也就是在此条件下Kirkendall面将向富Ti一侧移动。图8所示为Ti/Zr扩散偶在1 673 K时的Kirkendall速率曲线。由图8可以看出,Ti/Zr扩散偶在温度T=1 673 K下形成稳定的Kirkendall面,并向富Ti一侧移动,所获得的结果与图7中的一致。
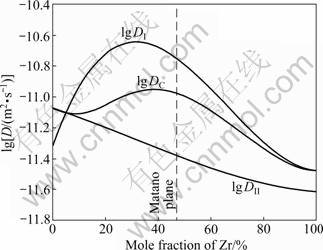
图7 本征扩散与相互扩散随Zr摩尔分数的变化
Fig.7 Changes of intrinsic diffusivities and interdiffusion with mole fraction of Zr
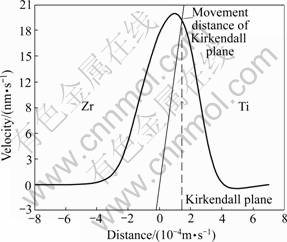
图8 1 673 K时Ti/Zr扩散偶的Kirkendall速率曲线
Fig.8 Kirkendall velocity curves of Zr/Ti diffusion couple at 1 673 K
4 结论
本研究评估文献中Ti-Zr二元体系BCC相的扩散实验结果,应用Calphad方法对其进行优化,建立Ti-Zr二元体系BCC相的扩散移动性数据库。在所获得的扩散移动性数据库的基础上,结合以Calphad为基础的热力学描述,成功地模拟Ti-Zr二元半无限扩散偶实验,获得的浓度分布曲线与实验具有很好的一致性。同时,对Ti-Zr合金的Kirkendall面的微观组织稳定性进行的研究,预测Kirkendall面的移动。通过与文献中实验数据的全面比较,可以看出所获得的扩散移动性数据库能很好地符合实际情况。因此,可以采用本研究所获得的扩散移动性数据库来模拟Ti合金体系的扩散控制过程。
REFERENCES
[1] 王金友, 葛志明, 周彦邦. 航空用钛合金[M]. 上海: 上海科学技术出版社, 1985.
WANG Jin-you, GE Zhi-ming, ZHOU Yan-bang. Titanium for aero application [M]. Shanghai: Shanghai Science and Technology Press, 1985.
[2] CUI Y W, KOYAMA T, OHNUMA I. Simulation of hexagonal- orthorhombic phase transformation in polycrystals [J]. Acta Materialia, 2007, 55(1): 233-241.
[3] KUMARA H C, WOLLANTSP, DELAEYL. Thermodynamic assessment of the Ti-Zr system and calculation of the Nb-Ti-Zr phase diagram [J]. Journal of Alloys and Compounds, 1994, 206(1): 121-127.
[4] CHEN Q, MA Ning, WU Kai-sheng, WANG Yun-zhi. Quantitative phase field modeling of diffusion-controlled precipitate growth and dissolution in Ti-Al-V [J]. Scripta Materialia, 2004, 50(4): 471-476.
[5] LIU Ya-jun, ZHANG Li-jun, YU Di. Computational study of mobilities and diffusivities in bcc Ti-Zr and bcc Ti-Mo alloys [J]. Journal of Phase Equilibria and Diffusion, 2009, 30(4): 334-344.
[6] K?HLER U, HERZING C. On the anomalous self-diffusion in BCC-titanium [J]. Phys Stat Sol (b), 1987, 144: 243.
[7] WALS?E N, de DECA, LIBANATI C M. Autodiffusion de titanio beta y hafnio beta [J]. Acta Metall, 1968, 16: 1297-1305.
[8] MURDOCK J, LUNDY T S, STANSBURY E E. Diffusion of Ti44 and V48 in titanium [J]. Acta Metall, 1964, 12: 1033-1039.
[9] MEHRER H, HERZIG C, STOLWIJK N A, BRACHT H. Titanium self-diffusion and chemical diffusion in bcc Ti-Al alloys [J]. Def Diff Forum, 1997, 143(147): 437-442.
[10] LUNDY T S. Diffusion in bcc metals Zr , Va , Ni, and Ta..Metals and Ceramics Division [D]. Knoxiviue: The University of Tennessee, 1964: 88-126.
[11] PATIL P V. Self-diffusion in Zr-Ag alloys [J]. Journal of Nuclear Materials, 1992, 187(197/203): 197-203.
[12] ZEERH, WATTERSJF, DAVIDSONRD. Diffusion and chemical activity of Zr-Sn and Zr-Ti systems [J]. Physical Review B, 1986, 34(10): 6895-6901.
[13] RAGHUNATHAN V R, TIWARI G R, SHARMA B D. Chemical diffusion in the bcc phase of the Zr-Ti alloy [J]. Metallurgical and Materials Transactions B, 1972, 3: 783-788.
[14] ARAKI H, MINAMINO Y, YAMANE T. Pressure dependence of anomalous diffusion of zirconium in bcc titanium [J]. Metallurgical and Materials Transactions A, 1996, 27(7): 1807- 1814.
[15] THIBON I, ANSEL D, GLORIANT T. Interdiffusion in bcc Ti-Zr binary alloys [J]. Journal of Alloys and Compounds, 2009, 470(1/2): 127-133.
(编辑 李艳红)
基金项目:凝固技术国家重点实验室自主课题资助项目(37-TP-2009)
通信作者:陈 逸; 电话: 15902958903; E-mail: chenyi880815@163.com