Coefficient of thermal expansion of stressed thin films

  WANG Zheng-dao(王正道), JIANG Shao-qing(蒋少卿)

Institute of Mechanics, School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China

Received 10 April 2006; accepted 25 April 2006

Abstract: A new technique was proposed to determine the coefficient of thermal expansion (CTE) of thin films at low temperature. Different pre-stress could be applied and the elastic modulus of materials at different temperatures was measured with CTE simultaneously to eliminate the influence of mechanical deformation caused by the pre-stress. By using this technique, the CTEs of polyimide/silica nanocomposite films with different silica doping levels were experimentally studied at temperature from 77 K to 287 K, and some characteristics related to this new technique were discussed.

Key words: thin film; thermal expansion coefficient; polyimide; elastic modulus; stress

1 Introduction

With the development of micro-electronics and micro-electro-mechanical systems (MEMS), new thin film materials and their related property studies are receiving more attentions since they are regarded as one kind of important functional materials in this field. For instance, considering their low thermal conductivity and high breakdown voltage, organic polymer films are often used as thermal and electrical insulating materials in MEMS[1]. However, the higher CTE of organic polymer films compared with that of the insulated substrates (e.g. ceramics or metals) will cause thermal stress build-up and even results in device failure through peeling and crack between the insulating film and substrates. Therefore, to ensure the reliability of the device in the application, the CTE of thin films must be characterized before time.

Based on the reported studying results, the mechanical properties (e.g. the residual stress[2], elastic constant [3] and Poisson’s ratio [4]) of thin films may not be the same as that of the bulk materials, and it is more reliable to directly characterize the mechanical properties from the thin film to be determined. About CTE measurement, some traditional techniques have been developed for bulk materials[5-9], but they are not suitable for thin films. Although some new techniques  were especially designed for thin films, e.g. the techniques of X-ray diffraction[10], micro-cantilever and micro-bridge[11], they are often limited for some special materials. For instance, the X-ray diffraction method is only appropriate for crystalline structure. Micro-cantilever and other related techniques are not suitable for such specimens, like a paper, that only one dimension is under the order of sub millimeter or microns. Therefore, some more universal CTE testing techniques suitable for thin film materials must be developed. 

About the CTE experiment, there also has another topic deserving to be paid attention. Basically, the present available techniques on CTE measurement can be divided into two types. One is that there is no load applied on specimens during the testing process and the specimen keeps free-state, e.g. strain gauge technique and micro-machined cantilever technique. The other is that a certain pre-load is applied on specimens during the testing process, e.g. a constant compressive force applied through the rigid expansion probe to the specimen for the technique of thermal mechanical analyzer (TMA), the mass of a quartz-rod applied through the rigid expansion probe to the specimen for the technique of quartz-tube dilatometer. For bulk materials, since the cross-sectional area is much larger than that of thin films, the load-induced pre-stress is very small and can be neglected. But for thin films, it may be different. Moreover, pre-stress state, which is caused by thermal and mechanical loads, the question asked here is that whether CTE may change for the case of stressed-body thermal expansion. ZHU et al [12] ever tried to give a study on this topic, but since they neglected the effect of the temperature on elastic modulus of materials, the experimental result is much higher than ever reported value.

In this paper, the theoretical analysis about CTE experiment of pre-stressed body was given and a new CTE testing device suitable for all thin films was introduced. By this device, the CTE of polyimide/silica(PI/SiO₂) nanocomposite films with different silica doping levels from low temperature (77 K) to room temperature (287 K) was researched.

2 Testing techniques

2.1 Testing principle for stressed specimens

Assuming there is no thermal stress at room temperature (T₀), the pre-stress and strain are named σ₀ and ε₀ respectively, which are caused by applied pre-load, then

                                  (1)

where  E corresponds to the elastic modulus of specimens at temperature T₀.

Since the change of the cross-sectional area of film specimen is much smaller than that of their length, σ₀  could be regarded as a constant during the CTE testing process. Therefore, the strain difference at different temperatures of T₀ and T₁ can be calculated by

              (2)

where E₁ and ε₁ are elastic modulus and strain at temperature T₁ espectively; α₀ corresponds to the linear CTE between T₀ and T₁. According to Eqn.(2), the strain difference, Δε₀, consists of two parts. One is caused by the thermal deformation and the other is caused by the chang of the elastic modulus. Eqn.(2) can also be expressed as

                 (3)

Therefore, the linear CTE for a universal differential temperature range, , can be expressed as                  

                     (4)

As stated above, the existing testing techniques for determining CTE include free-body (e.g. strain gauge technique) and constant-stressed-body specimens (e.g. quartz-tube dilatometer technique). In fact, it is impossible that a film like a piece of paper can be expanded effectively in a free state. In order to determine CTE values of thin films accurately, free-body techniques are not suitable and a tensile pre-stress must be applied. However, for CTE specimens with a certain pre-stress, the traditional testing techniques commonly neglect the influence of mechanical deformation and simplify Eqn.(4) as

                                    (5)

In fact, by using Eqn.(5) instead of Eqn.(4) to determine CTE under a constant pre-stress, one of the following conditions must be satisfied.

1) The pre-stress, σ₀, is small enough. This is often satisfied in some traditional CTE tests for bulking materials. However, since the cross-sectional area of thin films is much smaller than that of bulking materials, a larger stress will be existed in the films under the same load. Moreover, up to now, the CTE was calibrated based on free-state specimen or approximate free-state specimen. Although materials in the application are commonly under a certain force, no enough attentions were paid on the potential influence of pre-stress on CTE testing result. As considering this question, the pre-stress will become too larger to be neglected, as shown in Ref.[12].

2) The elastic modulus of specimens does not depend on the testing temperatures and keeps constant during CTE measurement. Unfortunately, the elastic modulus for most materials is temperature-dependence, e.g. the elastic modulus for some metals from room temperature to 77 K might increase about more than 50% and even 1-2 times for some polymer materials. Therefore, as determining CTE of constant-stressed-body thin films, the possible effect caused by the tensile stress-induced-strain must be considered.

2.2 Testing process and apparatus

According to Eqn.(4), in order to determine the linear CTE in a certain temperature range, the strain difference and the elastic modulus at every testing temperature must be known. Unfortunately, the available research results about the elastic modulus of different materials are often limited to some special temperature points, such as at the room temperature and 77 K. Therefore, for determining the CTE of constant-stressed-body films based on Eqn.(4), the elastic modulus of specimens at different temperatures must also be measured simultaneously.

In order to determining CTEs of thin films under different stress levels, a new cryogenic CTE testing device was designed in this study. The scheme of the testing device is shown in Fig.1. The specimen (11) is fixed by four magnets and magnet-sheaths (the magnet and magnet-sheath are shown as part 7 in Fig.1). The left-side magnet and magnet-sheath are installed on the foundation (3) by the supporting rod (6) and cannot move during the experiment. The right side connecting with the weights (13) by a wire can move smoothly along the surface of the temperature-controlled block (10) by the pulley system (12). The pulley system is specially designed for the application in low temperature with all parts made of the same material (stainless steel) to avoid the influence caused by different CTEs. The force level applied on the specimen can be adjusted by selecting different weights (13) (according to our study, the resistance caused by the pulley system can be neglected). The fixed rode (2) and the foundation (3) are made of stainless steel and have a lower thermal conductivity than that of copper. There are two functions for the fixed rode (2). Its upper part is a screw-thread structure, which can ensure that the temperature-controlled block (10) and the foundation (3) contact each other firmly. Another function is to prevent the testing temperature from increase too quickly while the altitude of liquid nitrogen is lower than that of the lower surface of the foundation (3). In this experiment, liquid nitrogen will be used as a cooling medium to decrease the testing temperature. Of course, in order to determine the CTE at lower temperature, some other medium, such as liquid helium, can be used instead of liquid nitrogen for temperature control.

During the experiment, the specimen (11) keeps contacting with the temperature-controlled block (10) tightly through a notch in the middle of the temperature-controlled block (10) so that the temperature of the specimen is more homogeneous, which is not shown in Fig.1. The temperature-controlled block (10) is made of copper which has a very high thermal conductivity. In the experiment, every temperature point was kept for five minutes for achieving good temperature stability. Considering the direct contact between the tem-

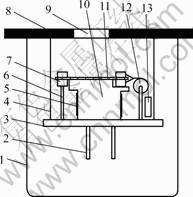
Fig.1 Scheme of device for measuring CTE of thin films at cryogenic temperature: 1—Dewar; 2—Fixed rod;   3—Foundation; 4—Connecting rod; 5—Heater;  6—Supporting rod;  7—Magnet and its sheath;  8—Flange;  9—Glass window;  10—Temperature-controlled block; 11—Specimen;  12—Pulley system; 13—Weight

perature-controlled block (10) and the specimen (11), and the micrometer thickness of the specimen, it is reasonable to believe that there is no temperature difference between (10) and (11). The testing temperature can be controlled by a heater (5) and  recorded by a thermometer, which is installed in the temperature-controlled block (10) and not shown in Fig.1. The power of the heater (5) is controlled by a standard temperature-controller installed in the outside of the liquid nitrogen Dewar (1).

Two reference lines are made on the specimen by optical method in advance. During the testing process, the distance of the two reference parallel lines is recorded by a microscope through the glass window (9), which decreases or increases due to the thermal deformation of the film specimen when the temperature drops or rises. The microscope is fixed in the outside of the liquid nitrogen Dewar (1) and not shown in Fig.1.

Two different weights (13) are used in the experiment, and one of them can be lifted freely. At every testing temperature, the specimen is drawn by respectively one weight and two weights through a simple adjusting setup. Therefore, the elastic modulus at each temperature can be easily calculated by recording the deformation difference of two times. Of course, it must ensure that the deformation is limited in the linear elastic range.

3 Results and discussion

By using this device, the CTE of PI/SiO₂ nanocomposite films were researched in this study. The testing temperature was from 287 to 77 K. PI/SiO₂ nanocomposite films studied here are synthesized by using sol-gel process including two steps [14]: hydrolysis of alkoxides to produce hydroxyl groups, followed by the polycondensation of the hydroxyl groups and residual alkoxides groups to form a three-dimensional network. Five different types of films were finally prepared according to the differences of silica doping levels(in mass fraction): 0, 1 %, 3% , 5%, 8%, 10% and 15%. The size of specimens is 140 mm×9.8 mm×32 μm(length×width×thickness) and the distance of the two reference lines is 80 mm.

Fig.2(a) shows the testing result of the temperatures effect on the elastic modulus for different PI/SiO₂ nanocomposite films. It clearly demonstrates that the elastic modulus of all measured films is strongly dependent on temperatures. With the temperature decreasing from 287 to 77 K, the elastic modulus has a dramatic increase, and a non-linear relationship exists. As the temperature decreases to about 126 K, the increasing tendency becomes slowly with further decrease of temperatures.

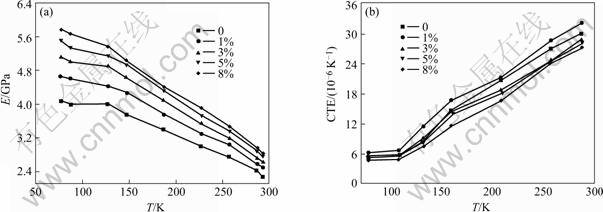
Fig.2 Temperature effect on elastic modulus (a) and CTE (b) of PI/SiO₂ films with different silica doping levels

The relationship of CTEs versus temperatures for different PI/SiO₂ nanocomposite films from 77 to 287 K is shown in Fig.2(b), which was obtained under fixed pre-apply stress of 3%-4.5% material’s UTS (the percentage variation is due to the material’s UTS changing at different temperatures). Plots in Fig. 2(b) indicate that the CTE of PI/SiO₂ composite films decreases quickly from about 110 K to 287 K (room temperature) and a nearly linear relationship between CTE and temperature exists. Further decreasing the testing temperature, the change of CTEs becomes slowly. The CTE value at liquid nitrogen temperature (77 K) is less than one fifth of that at room temperature (287 K).

The average CTE of PI/SiO₂ nanocomposite films with different silica doping levels from 77 K to 287 K is shown in Fig.3(a). Fig.3(b) gives the theoretical and experimental result of CTEs at room temperature. The theoretical result was calculated based on Eshelby theory. It is interesting to find that the theoretical result is much close to that of the experimental values at low silica doping levels, although the potential effect of the nano-size of the reinforcement was not considered and only the traditional meso-mechanical method was used in this study. More introduction about the calculating process of PI/SiO₂ composite CTE can be referred[13]. According to Fig.3(a), with increasing of silica doping levels, the composite CTE increases at first (1% silica), then has a quick decrease. As the silica doping level is higher than 10%, the change becomes slowly. The first increase at 1% SiO₂ is caused by the effect of the volume modulus of the reinforcement which is much higher than that of the PI matrix, because the composite CTE is not only decided by the CTE of the reinforcement and matrix, but also affected by their volume modulus. More detailed analysis can be found in Ref.[14]. As the silica content is higher than 10%, the measured CTE decreases slowly with increasing of silica content (Fig.3(a)) and is much higher than the theoretical prediction (Fig.3(b)), which is

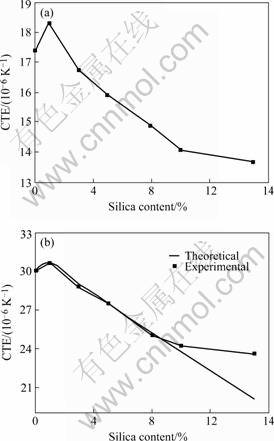
Fig.3 CTE influenced by silica doping levels: (a) Average CTE between 287 K and 77 K; (b) Theoretical and experimental result of CTE at room temperature

caused that it is difficult to disperse silica into PI matrix effectively with too higher silica doping level. As images shown in Figs.4 and 5 examined by SEM technique, there are noticeable white beads in the photographs of 15% silica-content films, which means that the average diameter of the dispersed silica particle is no longer in

Fig.4 Fractured surface morphologies of composite films with different silica contents at 287 K: (a) 1%; (b) 5%; (c) 15%

the nano-size.

4 Conclusions

The paper presents a new experimental method in determining CTE at low temperature. Compared to the traditional CTE testing techniques, the new method has some advantages for thin films, easy to be operated, different stress levels can be applied and the possible effect of the pre-stress on the CTE testing result considered. In this technique, the elastic modulus at every testing temperature point is measured so that the potential experimental error caused by the influence of the elastic modulus can be eliminated, which is very important for small cross-sectional-area specimens.

By using this new device, the CTE of PI/SiO₂ nanocomposite films with different silica contents was researched from 287 to 77 K. The predicted result based on Ashelby theory was also given. It is found that the

Fig.5 Fractured surface morphologies of composite films with different silica contents at 77 K: (a) 1%; (b) 5%; (c) 15%

composite CTE has a quick decrease as the silica content from 1% to 10%, then change slowly. At low silica content (lower than 10%), the testing result is much close to the theoretical value. As the silica content is higher than 10%, since it is difficult to disperse silica particles into PI matrix uniformly, which decreases the function of silica and leads to the real CTE value of composite films to be higher than that of the theoretical prediction. Moreover, with decreasing of the testing temperature, the CTE of PI/SiO₂ composite films decrease quickly at first, then slowly from about 110 to 77 K.

Acknowledgements

The authors are indebted to Professor FU Shao-yun and Mrs. LI Yan for their helping in providing specimens.

[1] WANG Z D, WEBER H W. Kapton film effect on the mechanical strength of ITER TF coil candidate insulation [J]. Mechanics of Materials, 2005, 37: 113-120.

[2] FANG W, WICKERT J A. Determining mean and gradient residual stress in thin films using micromachined cantilevers [J]. Micromech Microeng, 1996, 6: 301-309.

[3] TABATA O, KAWAHATA K, SUGIYAMA S, IGARASHI I. Mechanical property measurements of thin films using load-deflection of composite rectangular membrances [J]. Sensors and Actuators A, 1989, 20: 135-141.

[4] VLASSAK J J, NIX W D. A new bulge test technique for determination of elastic modulus and Poisson’s ratio of thin films [J]. J Mater Res, 1992, 7: 3242-3249.

[5] JONES R V, Recording optical lever [J]. J Sci Instrum, 1959, 36: 90-92.

[6] SHAPIRO J M, TAYLOR D R, GRAHAM G M. A sensitive dilatometer for use at low temperatures [J]. Can J Phys, 1964, 42: 835-847.

[7] KINZLY R E. A new interferometer capable of measuring small optical path differences [J]. Appl Opt, 1967, 6: 137-140.

[8] JACOBS S F, BRADFORD J N, BERTHOLD J W. Ultraprecise measurement of thermal expansion coefficients [J]. Appl Opt, 1970, 9: 2477-2480.

[9] Annual Book of ASTM Standards. Standard Test Method for Linear Thermal Expansion of Solid Materials by Thermomechanical Analysis[R]. E 831-00, 2000: 273-276.

[10] BATCHELDER D N, SIMMONS R O. X-ray lattice constants of crystals by a rotating camera methods: Al, Ar, Au, Ge, Ne, Si [J]. J Chem Appl Phys, 1965, 36: 2864-2868.

[11] FANG W, LO C Y. On the thermal expansion coefficients of thin films [J]. Sensors and Actuators A, 2000, 84: 310-314.

[12] ZHU H, LI W, TSENG A A. Measurement of CTE at reduced temperature for stressed specimens[A]. NETTLES A T, ZUREICK A. American Society for Testing and Materials[C]. West Conshohocken: PA, 2002: 374-377.

[13] JIANG S H. CTE Study of PI/SiO₂ Nanocomposite Thin Films at Low Temperature[D]. Beijing: CAS, 2006. (in Chinese).

[14] WANG Z D, LU J J，LI Y, FU S Y, JIANG S Q, ZHAO X X. Studies on thermal and mechanical properties of PI/SiO₂ nanocomposite films at low temperature [J]. Composite Part A, 2006, 37: 74-79.

(Edited by YANG Hua)

Foundation item: Project (TJJ05005) supported by the National Natural Science Foundation of China and Beijing Jiaotong University

Corresponding author: WANG Zheng-dao; Tel: +86-10-51687257; Fax: +86-10-51682094; E-mail: zhdwang@center.njtu.edu.cn