Optimal selection of annulus radius ratio to enhance heat transfer with minimum entropy generation in developing laminar forced convection of water-Al2O3 nanofluid flow
来源期刊:中南大学学报(英文版)2017年第8期
论文作者:Siavashi Majid Jamali Mohammad
文章页码:1850 - 1865
Key words:nanofluid; heat transfer enhancement; forced convection; entropy generation; annulus; radius ratio
Abstract: Heat transfer and entropy generation of developing laminar forced convection flow of water-Al2O3 nanofluid in a concentric annulus with constant heat flux on the walls is investigated numerically. In order to determine entropy generation of fully developed flow, two approaches are employed and it is shown that only one of these methods can provide appropriate results for flow inside annuli. The effects of concentration of nanoparticles, Reynolds number and thermal boundaries on heat transfer enhancement and entropy generation of developing laminar flow inside annuli with different radius ratios and same cross sectional areas are studied. The results show that radius ratio is a very important decision parameter of an annular heat exchanger such that in each Re, there is an optimum radius ratio to maximize Nu and minimize entropy generation. Moreover, the effect of nanoparticles concentration on heat transfer enhancement and minimizing entropy generation is stronger at higher Reynolds.
Cite this article as: Siavashi Majid, Jamali Mohammad. Optimal selection of annulus radius ratio to enhance heat transfer with minimum entropy generation in developing laminar forced convection of water-Al2O3 nanofluid flow [J]. Journal of Central South University, 2017, 24(8): 1850-1865. DOI: https://doi.org/10.1007/s11771-017-3593-7.
J. Cent. South Univ. (2017) 24: 1850-1865
DOI: https://doi.org/10.1007/s11771-017-3593-7

Siavashi Majid, Jamali Mohammad
Applied Multi-Phase Fluid Dynamics Lab., School of Mechanical Engineering,
Iran University of Science and Technology, Tehran, Iran
 Central South University Press and Springer-Verlag GmbH Germany 2017
Central South University Press and Springer-Verlag GmbH Germany 2017
Abstract: Heat transfer and entropy generation of developing laminar forced convection flow of water-Al2O3 nanofluid in a concentric annulus with constant heat flux on the walls is investigated numerically. In order to determine entropy generation of fully developed flow, two approaches are employed and it is shown that only one of these methods can provide appropriate results for flow inside annuli. The effects of concentration of nanoparticles, Reynolds number and thermal boundaries on heat transfer enhancement and entropy generation of developing laminar flow inside annuli with different radius ratios and same cross sectional areas are studied. The results show that radius ratio is a very important decision parameter of an annular heat exchanger such that in each Re, there is an optimum radius ratio to maximize Nu and minimize entropy generation. Moreover, the effect of nanoparticles concentration on heat transfer enhancement and minimizing entropy generation is stronger at higher Reynolds.
Key words: nanofluid; heat transfer enhancement; forced convection; entropy generation; annulus; radius ratio
1 Introduction
Nowadays nanofluids are well known in industrial applications. Addition of the solid nanoparticles to a base fluid improves thermophysical properties of the fluid. Size, type and concentration of nanoparticles are important parameters affecting the thermal properties of the base fluid. The use of nanofluids instead of conventional fluids such as water, oil and ethylene glycol is one of methods for heat transfer enhancement. The thermal conductivity is a principal parameter of nanofluid which shows that heat transfer characteristics can be improved by means of nanofluids [1-3].  and PRAMUANJAROENKIJ [4] conducted a review of convective heat transfer enhancement with nanofluids. From their literature, capabilities of nanofluids to improve the performance of thermal engineering systems are apparent.
and PRAMUANJAROENKIJ [4] conducted a review of convective heat transfer enhancement with nanofluids. From their literature, capabilities of nanofluids to improve the performance of thermal engineering systems are apparent.
Heat transfer characteristics of nanofluids are studied in many different geometries such as circular tubes [5], exponentially shrinking sheets [6], stretching surfaces [7, 8], and channels [9]. Concentric annular pipe is an important geometry which is used in widespread industrial applications like heat exchangers, gas turbines, oil production wells and so on. IZADI et al [10] studied laminar forced convection of water-Al2O3 nanofluid numerically inside an annulus. They showed that the volume fraction of nanoparticles has a strong effect on the temperature profile. However their effect on the dimensionless axial velocity profile is negligible. ALAWI et al [11] applied two different boundary conditions at the surface of a horizontal concentric annulus. They investigated numerically natural convection heat transfer characteristics of a nanofluid flow in this geometry. MATIN and POP [12] studied mixed convection heat transfer of the water-Al2O3 nanofluid inside an eccentric annulus numerically. They discussed the variation of the mean Nusselt number by the eccentricity, the Reynolds number, the volume fraction of nanoparticles and the Rayleigh number. Laminar mixed convection heat transfer of water-Al2O3 nanofluid inside an annulus with constant heat flux boundary conditions has been investigated by MOGHARIA et al [13]. They studied the effect of the mean diameter of nanoparticles on the hydrodynamics and the thermal characteristics. YANG et al [14] proposed a theoretical analysis of forced convective heat transfer of nanofluids inside a concentric annulus. Beside the effect of nanoparticle volume fraction and nanoparticle type on the pressure gradient and the Nusselt number, they also revealed the effects of Brownian and thermophoretic diffusivity ratios. DAWOODA et al [15] summarized important findings on forced, natural and mixed-convection heat transfer of flows inside annuli and present an overview of recent research on this topic.
Entropy generation analysis can be used as a tool for analyzing thermal systems in order to determine optimal condition of systems [16]. Many researchers applied this tool to investigate nanofluid flow in various geometries with different boundary conditions. BIANCO et al [17] performed a numerical study on developing turbulent convection heat transfer of water-Al2O3 nanofluid inside a square tube. In addition, they used an analytical procedure for entropy generation analysis and compared their results with those of their numerical study. Both approaches could find an optimal Reynolds number to minimize the entropy generation. BIANCOA et al [18] conducted an study on entropy generation of turbulent forced convection of water-Al2O3 nanofluid inside a circular tube. They discussed the effect of different inlet conditions and nanoparticles concentration on the entropy generation and concluded that the optimal concentration of nanoparticles is along with low Reynolds numbers. LEONG [19] conducted an analytical study on entropy generation analysis of nanofluid flow in a circular tube. In their study, the base fluid was water and two types of nanoparticles; alumina and titanium dioxide were utilized. They showed total dimensionless entropy generation of titanium dioxide nanofluids is lower with respect to alumina nanofluids. MOGHADDAMI et al [20] proposed an analytical analysis of entropy generation of nanofluid flow in turbulent and laminar regimes inside a circular pipe. They showed entropy generation increases with an increase in nanoparticles when irreversibility of the fluid flow is dominant. Afterwards, MOGHADDAMI el al [21] presented a numerical analysis to investigate entropy generation of the previous problem. They determined an optimum Reynolds number in turbulent regime to minimize the entropy generation of flow inside a pipe. They concluded that this optimum Reynolds value depends strongly on the volume fraction of the nanofluid and by increasing the volume fraction the value of the optimum Re decreases. Recently, YARMAND et al [22] studied entropy generation of nanofluid in turbulent flow inside a square tube. They reported the effects of nanoparticles volume fraction, inlet conditions, size and type of nanoparticles on entropy generation.
In addition to analysis of entropy generation in tubes, other geometries such as microchannels, parallel disk systems, heat exchangers and stretching sheets have been investigated by many researchers and interested readers are referred to Ref. [23] to review these topics.
Some researchers studied entropy generation of a base fluid inside annuli [24, 25]. MAHMUD and FRASER [26] presented an analytical analysis on entropy generation inside a cylindrical annulus with a relative rotational motion. HADDAD et al [27] studied entropy generation of a base fluid due to laminar forced convection in the entrance region of a concentric annulus. They concluded that an increase in Eckert number or the radius ratio causes entropy generation to increase. SIAVASHI et al [28, 29] studied nanofluid forced convection inside annuli partially filled with porous media and also equipped with porous ribs and found the optimal operating conditions. They also analyzed their problem from the viewpoint of the second law of thermodynamics. Another entropy generation study was done for turbulent flow of TiO2-water nanofluid inside annuli [30]. To further read about different applications of entropy generation study, readers are referred to Refs. [31-34].
From the literature, it can be concluded that parameters such as radius ratio of annulus, Reynolds number, volume fraction of nanoparticles and wall heat flux have strong effects on heat transfer enhancement and entropy generation of flow in annuli. In many heat transfer problems, engineers concern to select an appropriate annulus – to have maximum heat transfer enhancement or minimum entropy generation – from annuli with different radius ratios and the same flowing areas. The question is here that, which radius ratio and what concentration of nanoparticles can provide the maximum heat transfer enhancement or minimum entropy generation. In other words, which combination of radius ratio and nanofluid at a specific Reynolds can lead to the maximum heat transfer enhancement or the minimum entropy generation?
To the knowledge of authors, in developing laminar forced convection flow of nanofluids in annuli with different radius ratios and same cross sectional areas, the effects of the above mentioned parameters on entropy generation and heat transfer have not been investigated yet.
Two different common methods are available to calculate the entropy generation of flow; which we call them the integral and the differential approaches. Results of these two methods to determine entropy generation have not been compared with each other. In some research a formulation proposed by BEJAN [35] are employed that is appropriate to calculate entropy generation in a heat exchanging tube. While, there is a need to specify the capability of this formulation for various geometries.
In this work, the approved fluid mixture models are used to calculate the thermophysical properties of nanofluid and the governing equations are solved numerically. In our study, entropy generation in an annulus is calculated by the integral and the differential approaches and results are compared to select the appropriate approach. Both of the entropy generations due to the friction and heat transfer are considered separately. The optimal conditions to have higher heat transfer enhancement and to minimize the entropy generation are discussed and the effect of different parameters on the optimal conditions are presented.
2 Methodology
2.1 Problem description
In this work, laminar forced convective heat transfer of water-Al2O3 nanofluid, considering combined thermal and hydrodynamic entry regions, inside an annulus subjected to constant surface heat flux at inner/outer wall is investigated. For the first case, the inner surface is adiabatic and the outer surface is exposed to a constant heat flux. Boundary conditions at walls for the second case are opposite to the first one. Figure 1 exhibits a schematic of the geometry of the problem with its boundary conditions.

Fig. 1 Geometrical configuration and boundary conditions of problem
The flow inside the annulus is assumed to be axisymmetric. The length of the annulus is 1 m and different radius ratios–inside radius to outside radius – are considered to be in the range of 0.2-0.8, provided the cross sectional area is fixed.
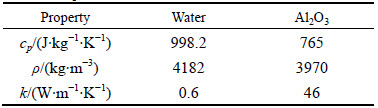
The flow is assumed to be steady, laminar, and incompressible. The study is conducted for a range of Reynolds numbers from 200 to 1500, three volume fractions of nanofluid (0%, 2% and 4%) and wall heat flux of 15000 W/m2. The fluid enters the annulus with uniform temperature of 293 K.The physical property of water and Al2O3 are given in Table 1.
Table 1 Properties of water and Al2O3 at 293 K
2.2 Governing equations and nanofluid properties
With a single phase approach – using the mixture properties–under steady state condition, the continuity, the linear momentum and the energy equations for nanofluid can be written respectively as
 (1)
(1)
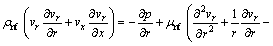
 (2)
(2)

 (3)
(3)
 (4)
(4)
where ρnf, μnf, cp,nf and knf are the density, viscosity, specific heat capacity, and thermal conductivity of the nanofluid, respectively, which are determined using the mathematical formulations presented by Eqs. (5)-(14).
It is assumed that nanoparticles are distributed homogeneously throughout the base fluid and there are no inter-phase interactions in the momentum and the energy transport. Therefore, effective properties are defined as a function of the concentration of nanoparticles, to model properties of the nanofluid.
The density of nanofluid is calculated as follows [36]:
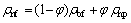 (5)
(5)
where φ is the volume fraction of nanoparticles, and subscripts “nf”, “bf” and “np” refer to nanofluid, base fluid and nanoparticle respectively.
For calculation of the effective specific heat of the nanofluid, it is assumed that the base fluid and nanoparticles are in thermal equilibrium. Using the following formula [37]:
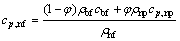 (6)
(6)
The above mentioned relations which are based on mixture rules are validated through numerous experimental studies [37-39].
According to KOO and KLEINSTREUER [40] by adding the effect of Brownian motion to the thermal conductivity of a static dilute suspension, the thermal conductivity of nanofluid can be estimated by
 (7)
(7)
Based on Maxwell’s model [41], the relation for kstatic can be described as
 (8)
(8)
To consider the effect of the temperature on the thermal conductivity of the base fluid, Eq. (9) is proposed by HAGEN [42] for thermal conductivity of water as the base fluid.
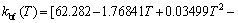
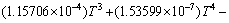
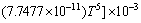 (9)
(9)
For the thermal conductivity due to Brownian motion in Eq. (7), KOO and KLEINSTREUER [40] presented an expression in the following way:
 (10)
(10)
where κ=1.38×10-23 J/K is the Boltzmann constant, D is the nanoparticle diameter and cnp is the effective specific heat of the nanofluid. A correlation for the fraction of the liquid volume β for water-Al2O3 nanofluid is suggested by KOO and KLEINSTREUER [40]:
β=0.0017(100φ)-0.0841 (11)
RAISEE and MOGHADDAMI [43] based on the experimental data of DAS et al [44] expressed the following relation to model f(T, φ):
 (12)
(12)
Based on the experimental study of REA et al [45], the viscosity of the nanofluid is correlated as follows:
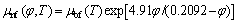 (13)
(13)
HAGEN [42] also suggested a correlation to consider the effect of temperature on the viscosity of water:
 (14)
(14)
2.3 Boundary conditions
The governing Eqs. (1)-(4) are solved subject to the following boundary conditions:
At the inlet of the annulus (x=0):

At the inner wall of the annulus (r=ri):

At the outer wall of the annulus (r=ro):
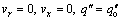
At the outlet of the annulus (x=L), the pressure is assumed to be equal to the outlet pressure.
2.4 Entropy generation
Entropy generation is due to the presence of irreversibilities and consists of two main parts. The volumetric rate of total entropy generation has been expressed by BEJAN [35] as follows:
 (15)
(15)
The first term is heat transfer irreversibility due to finite temperature difference and the second term – sometimes called friction entropy generation – is caused by fluid flow friction. These two independent terms may have either the same order of magnitude or not. The total entropy generation all over the domain can be calculated by integration of 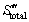 over the fluid domain (D) as follows:
over the fluid domain (D) as follows:
 (16)
(16)
To show the contribution of the heat transfer irreversibility in total irreversibility, a dimensionless parameter, the Bejan number (Be), is considered. The Bejan number (Be) is the ratio of the entropy generation due to heat transfer to total entropy generation. This dimensionless parameter can be described as
 (17)
(17)
When the value of Bejan number is close to 1, irreversibility is dominated by heat transfer.
In two following sub-sections, two different approaches to determine each term of total entropy generation are represented.
2.4.1 Differential approach
To evaluate the rate of entropy generation per unit volume of fluid, BEJAN [35] showed that each term of the total rate of entropy generation can be calculated utilizing the following relations:
 (18)
(18)
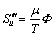 (19)
(19)
where T is the local absolute temperature and Ф is the viscous dissipation function. In 2D Cartesian coordinates, the above mentioned terms become:
 (20)
(20)
 (21)
(21)
Summation of these terms results the total rate of entropy generation and then by integration over the whole domain, the total entropy generation in whole flow field can be determined by Eq. (16).
2.4.2 Integral approach
BEJAN [35] provides the following correlation for fully developed flow inside a heat exchanger tube with flow passage length of dx to calculate the rate of entropy generation per unit length:
 (22)
(22)
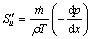 (23)
(23)
where q′, ΔT,  dp/dx, ρ and T are the wall heat transfer per unit length, difference between the wall temperature and the bulk temperature of fluid, the mass flow rate, the pressure gradient, the bulk density of the fluid and the bulk temperature of the fluid, respectively.
dp/dx, ρ and T are the wall heat transfer per unit length, difference between the wall temperature and the bulk temperature of fluid, the mass flow rate, the pressure gradient, the bulk density of the fluid and the bulk temperature of the fluid, respectively.
The bulk temperature of the fluid are expressed as
 (24)
(24)
where Tin and Tout are inlet and outlet temperatures, respectively.
For flow inside a channel with hydraulic diameter of Dh, the heat transfer and friction terms of entropy generation become
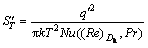 (25)
(25)
 (26)
(26)
where q′, k, Nu and f are the wall heat flux, the bulk thermal conductivity of fluid, the Nusselt number and the friction factor, respectively.
2.5 Numerical method and validation
In the present work, a CFD code is developed to solve our problem. The governing Eqs. (1) to (4) with the prescribed boundary conditions are discretized using the finite volume method. The second order upwind scheme is used for discretization of the convective terms and diffusive terms are approximated with the second order central scheme. The SIMPLE algorithm of PATANKAR and PATANKAR [46] is employed for the velocity-pressure coupling. After solving the flow and heat equations, grid-independency check has been done by refining the solution grids. Proper grid consisted of 750 segments in the axial (x) direction and 15 to 45 segments for different radius ratios in the radial (r) direction.
In order to validate the results of the numerical code, fully developed laminar flow of pure water inside a concentric annular duct subject to constant heat fluxes at walls is simulated numerically and results containing the friction factor and the average Nusselt number are compared with the data presented by ROHSENOW et al [47]. To confirm the validity of friction factor coefficient, a range of Reynolds numbers from 100 to 1500 are studied for an annulus with ri/ro=0.2. Figure 2 compares the friction factor coefficients obtained by the numerical method and the correlation (27) presented by ROHSENOW et al [40]:
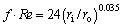 (27)
(27)
Equation (27) represents the average friction factor (f ) of an annulus. The average friction factor in annuli is defined as [32]
 (28)
(28)
where fi and fo represent the friction factor at the inner and the outer walls of an annulus, respectively.
To confirm the validity of the estimated Nusselt number by the CFD code, the results of numerical simulation are compared with the data which are reported by ROHSENOW et al [47]. Hence pure water flow with Re=50, exposed to the following three kinds of thermal boundary conditions:
(1) First kind: Uniform wall heat flux at outer wall; the inner wall is insulated;
(2) Second kind: Uniform wall heat flux at inner wall; the outer wall is insulated;
(3) Third kind: Uniform wall heat flux at both walls.
In Fig. 3, the Nusselt number is exhibited as a function of the radius ratio, for the three above mentioned thermal boundary conditions.
Figures 2 and 3 indicate that for different aspect ratios and boundary conditions, the numerical results are in good agreement with the data of ROHSENOW et al [47]. Therefore, our numerical CFD code is reliable andcan be employed for analysis of entropy generation and heat transfer of forced convection of flow inside an annulus with various radius ratios.
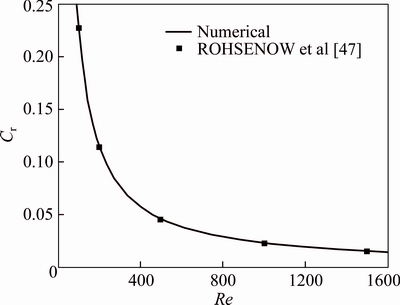
Fig. 2 Comparison of computed friction factor coefficient with data of ROHSENOW et al [47], for fully developed laminar flow of water inside an annulus with ri/ro=0.2

Fig. 3 Comparison of computed Nusselt number with data of ROHSENOW et al [47], for fully developed laminar flow of water inside an annulus (Results are presented as a function of radius ratio of an annulus and for three kinds of thermal boundary conditions)
3 Results and discussion
In this section, results are presented and the effects of different thermal boundary conditions, Reynolds numbers and volume fraction of nanoparticles, on the heat transfer enhancement and entropy generation inside annuli with a specified cross sectional area and different radius ratios are discussed. In addition, the effect of volume fraction of nanoparticles on the Nusselt number and entropy generation are compared with those of the pure water.
3.1 Heat transfer enhancement
After numerical solution of the problem, temperature distribution in each section of the annulus is determined. The local heat transfer coefficient (h) for either the inner or the outer wall is calculated using the following equation:
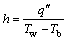 (29)
(29)
where Tw and Tb are the wall temperature and the bulk temperature of the fluid, respectively.
The average heat transfer coefficient is determined by an expression of the form:
is determined by an expression of the form:
 (30)
(30)
In this work, the wall heat flux (q″) is assumed to be constant and uniform along the walls, hence the wall temperature varies along the annulus. Knowing the value of thermal convection coefficient the average Nusselt number can be determined by
 (31)
(31)
In this relation, the thermal conductivity of the nanofluid is calculated at the mean temperature of the nanofluid.
3.1.1 First kind of thermal boundary condition
For the first kind problem introduced at Section 2.5 – insulated inner wall and constant heat flux at the outer boundary – the average Nusselt number for three values of nanoparticle volume fraction, 0%, 2% and 4%, are shown in Figs. 4-6. Obviously, the Nusselt number grows with increasing the Reynolds number, and this value is higher for lower values of the radius ratio. The effect of Re to promote the Nusselt number is much higher than the radius ratio and this effect is higher for lower values of radius ratio. As a consequence, at lower Reynolds numbers the difference between the Nusselt numbers of various radius ratios is small; while for higher Reynolds numbers this difference becomes more significant. For instance, at φ=2% and Re=200, decreasing the radius ratio from 0.8 to 0.2, leads to an increase of approximately 18% in the Nu, while for Re=1500 this figure is more than 30%. Therefore, for annuli with fixed cross sectional area, selection of the radius ratio has an important role in the heat transfer characteristics of the problem. Form Figs. 4-6, it can be seen that increasing the value of nanoparticle volume fraction, causes a noticeable growth in the Nusselt numbers.

Fig. 4 Nusselt number of pure water (φ=0%) on outer wall
The effect of nanoparticle volume fraction on the increment of Nusselt number at radius ratio of 0.2 is illustrated in Fig. 7. For volume fraction of 4% at Re=200, Nu is approximately 40% more than that value of the base fluid and for higher Reynolds numbers, this value increases such that for Re=1500 this figure approaches to 50%.
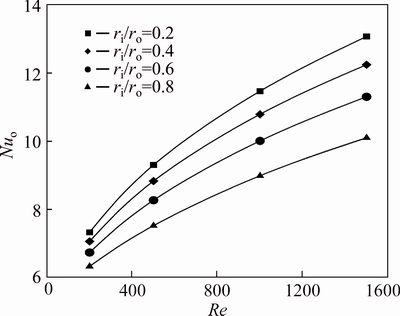
Fig. 5 Nusselt number of water-Al2O3 nanofluid (φ=2%) on outer wall

Fig. 6 Nusselt number of water-Al2O3 nanofluid (φ=4%) on outer wall

Fig. 7 Nusselt number of water-Al2O3 nanofluid on outer wall of annulus at radius ratio of 0.2
To further investigate effects of concentration of nanoparticles, Re and radius ratio on the Nu, the relative Nu number is defined as the ratio of the Nu number of the nanofluid to that of the base fluid. The relative Nu number reflects heat transfer enhancement by use of the nanofluid and compares it with the base fluid.
Figures 8 and 9 generally indicate that an increase in the Reynolds number enhances the effect of concentration on the increment of Nusselt number. For lower Reynolds, the effect of radius ratio on the relative Nu is higher and this effect can decline with increasing the Re. By the way, this effect is still high on heat transfer enhancement. For example for φ=4% at Re= 1500, the radios ratio can increase the relative Nu up to 9%, however at Re=200 this effect is approximately twice. Therefore, although the Nusselt number in lower Reynolds numbers is smaller than the Nusselt number in higher Reynolds values, but the effect of radius ratio on the increment of Nusselt number in lower Reynolds is much higher than higher ones.
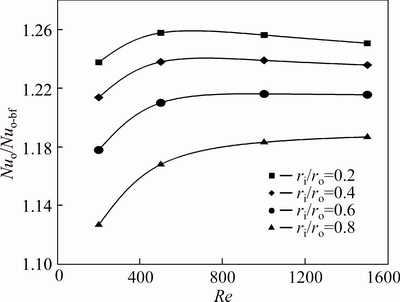
Fig. 8 Relative Nusselt number of water-Al2O3 nanofluid (φ=2%) on outer wall

Fig. 9 Relative Nusselt number of water-Al2O3 nanofluid (φ=4%) on outer wall
3.1.2 Second kind of thermal boundary condition
Figures 10-12 show the Nusselt number of inner surface of the annulus for three different nanoparticle volume fractions as a function of the Reynolds number. The general effects of the radius ratio, the Reynolds number and concentration of nanoparticles on the Nusselt number is similar to the previous case. However, in this case the effect of radius ratio is stronger than the previous problem, even for low Reynolds values. For instance at φ=2%, decreasing the radius ratio of annulus from 0.8 to 0.2, at Re=200 and Re=1500 can respectivelycause an enhancement of approximately 75% and 70% in the Nu. While for the first case, these values were 18% and 30% respectively. Furthermore, the difference between the Nu at radius ratios of 0.2 and 0.4 is higher than the difference at radius ratios of 0.6 and 0.8. This shows that the sensitivity of the Nusselt number to the change of radius ratio is stronger at lower radius ratios in comparison with higher ratios.

Fig. 10 Nusselt number of pure water (φ=0%) on inner wall

Fig. 11 Nusselt number of water-Al2O3 nanofluid (φ=2%) on inner wall

Fig. 12 Nusselt number of water-Al2O3 nanofluid (φ=4%) on inner wall
Figure 13 shows that the effect of nanoparticle volume fraction on the increment of Nusselt number at radius ratio of 0.2 is similar to the first case. But this effect for the first kind of thermal boundary condition is stronger. In this case, the Nusselt number approximately increases 30% by adding nanoparticles (φ=4%) at Re=200 and this value is 10% less than the first case.
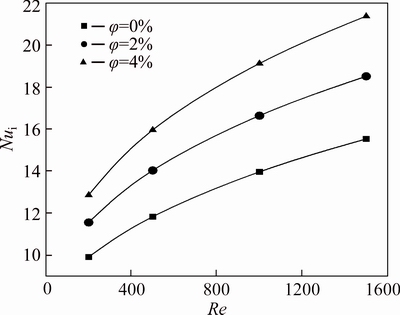
Fig. 13 Nusselt number of water-Al2O3 nanofluid on inner wall of annulus at radius ratio of 0.2
To further investigate the above mentioned effects on the Nu, the relative Nusselt number of the nanofluid to that of the base fluid are illustrated in Figs. 14 and 15. Unlike the first case, in this case the behavior of the relative Nusselt at different radius ratios is peculiar. For Re=200, the maximum effect of addition of nanoparticles on the Nusselt number corresponds to ri/ro=0.4, which for the first case, the relative Nu number is maximum at ri/ro=0.2. At this Re, the minimum Nu corresponds to ri/ro=0.8. Increasing the Re up to 1000, relative Nu of an annulus with ri/ro=0.4 rises with a higher rate than the relative Nu of ri/ro=0.2. Consequently, the highest impact of addition of nanoparticles on the Nu can be observed for ri/ro=0.4, 0.6, 0.2 and 0.8 successively. With more increase in the Re, the relative Nu of ri/ro=0.8 precedes the relative Nu value of ri/ro=0.2. Such that for Re=1500, the relative Nusselt of radius ratios of 0.4 and 0.2 is maximum and minimum, respectively. This phenomenon can be observed for both water-Al2O3 nanofluid slurries with φ=2% and 4%.

Fig. 14 Relative Nusselt number of water-Al2O3 nanofluid (φ=2%) on inner wall
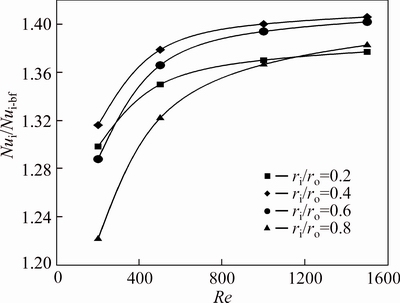
Fig. 15 Relative Nusselt number of water-Al2O3 nanofluid (φ=4%) on inner wall
Therefore, the nanoparticle volume fraction has the maximum effect on the increment of Nusselt number for annuli of ri/ro=0.4 with respect to the other radius ratios considered in this study.
It can be concluded that, for an annulus with constant cross sectional area, Nu and the relative Nu over the outer surface for ri/ro=0.2 are more than the other radius ratios, when the first kind of thermal boundary condition is applied on the wall surfaces. But for the second kind of thermal boundary condition, Nu and the relative Nu on the inner surface of the annulus are highest for radius ratios of 0.2 and 0.4, respectively. Furthermore, the minimum of relative Nu quite depends on the value of Re while the value of the relative Nu in ri/ro=0.4 is maximum.
Comparing Figs. 14 and 15 reveals that the heat transfer enhancement for the slurry with φ=4% is approximately 20% higher than the slurry with φ=2%.
3.2 Entropy generation analysis
In this section, the two methods which presented at Section 2.4 are employed for determination of the entropy generation of fully developed flow of nanofluid. First, results of the two approaches are compared for flows inside a pipe and also an annulus. Next, the effects of radius ratio, the concentration of nanoparticles, the Reynolds number and thermal boundary conditions on the entropy generation inside an annulus are investigated.
3.2.1 Comparison of entropy generation estimation methods
The integral approach for estimation of entropy generation is proposed by MOGHADDAMI et al [20] to be employed for fully developed flow in a circular pipe. In some research, this method has been employed for calculation of entropy generation inside different channels with non-circular cross sections by using the hydraulic diameter of channels. Entropy generation due to local velocity and temperature gradients has a strong effect on the total entropy generation of flow and these effects might be important for flows inside non-circular pipes. Accordingly, application of the hydraulic diameter can cause an error in estimation of the entropy generation in an annulus. In addition, the integral method of entropy generation is capable to estimate the entropy generation of fully developed flows and could not be used in developing flows. Hence, the differential approach should be employed to estimate the entropy generation of developing flows.
In order to compare these two approaches for calculation of entropy generation, first the entropy generation of fully developed laminar flow inside a circular pipe as a function of the Re is estimated using both the integral and the differential approaches. Second, the methods are employed to calculate the entropy generation of flow inside an annulus with the same hydraulic diameter to that of the circular pipe.
The hydraulic diameter of these geometries is set to be 0.006 m and the second kind of thermal boundary condition on an annulus with ri/ro=0.8 is applied. As exhibited in Fig. 16, for flow inside a pipe there is a good agreement between results of the integral and the differential methods for different Re values. But the difference between the total entropy generations in the annulus is extremely high for the exhibited range of Reynolds numbers. Therefore the integral approach for estimation of entropy generation is not capable for calculation of the entropy generation in an annulus.
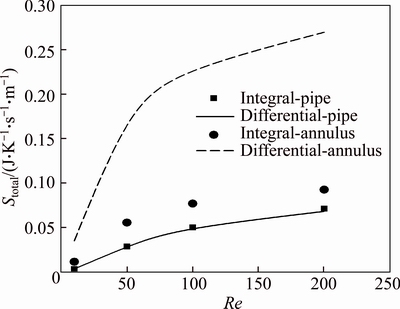
Fig. 16 Comparison of estimated total entropy generations, using integral and differential approaches, for fully developed laminar flow of water inside a pipe and an annulus
In the subsequent sections, the differential method is used for calculation of entropy generation of developing laminar flow inside an annulus.
3.2.2 First kind of thermal boundary condition
Figures 17-19 show the effects of varying radius ratios and Reynolds number on the friction entropy generation of pure water and water-Al2O3 slurry with φ=2% and φ=4%, respectively. Entropy generation due to friction effects depends strongly on the wetted area and the velocity of fluid. Hence, as can be seen inthese figures, higher radius ratios and Reynolds numbers leads to a higher friction entropy generation. Moreover, since the viscosity increases with an increase in the Al2O3 volume fraction, the friction entropy generation rises with increase of the concentration of nanoparticles. Figures 20 and 21 show the ratio of the friction entropy generation of nanofluid to that of the base fluid, for various radius ratios and Reynolds numbers. It can be seen that the volume fraction of nanoparticles has a significant effect on the increment of friction entropy generation. As is exhibited in Fig. 21, at concentration of 4%, the entropy generation ratio Su/Su-bf for ri/ro=0.8 at Re=1500 approaches the value of 24.5.
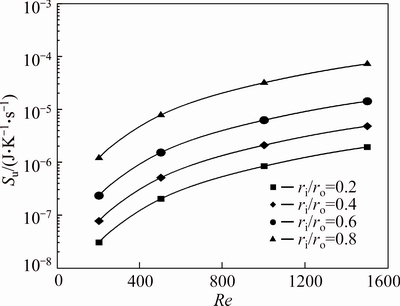
Fig. 17 Friction entropy generation of pure water (φ=0%) for first kind of thermal boundary condition

Fig. 18 Friction entropy generation of water-Al2O3 nanofluid (φ=2%) for first kind of thermal boundary condition
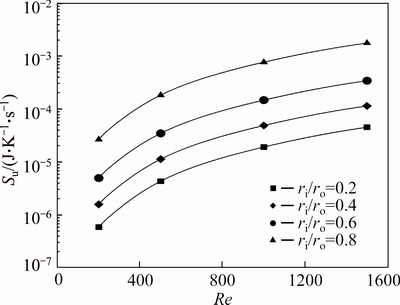
Fig. 19 Friction entropy generation of water-Al2O3 nanofluid (φ=4%) for first kind of thermal boundary condition
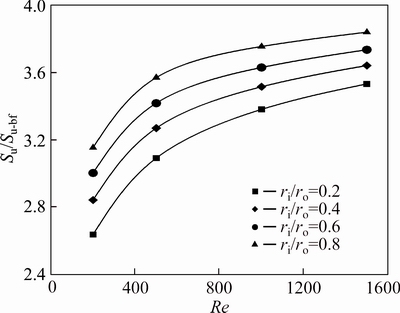
Fig. 20 Relative friction entropy generation of water-Al2O3 nanofluid (φ=2%) for first kind of thermal boundary condition

Fig. 21 Relative friction entropy generation of water-Al2O3 nanofluid (φ=4%) for first kind of thermal boundary condition
The entropy generation due to the heat transfer is shown in Figs. 22-24. These figures compare the heat transfer entropy generation of nanofluids for various concentrations of nanoparticles with different radius ratios as a function of Reynolds number. As depicted, the thermal entropy generation is extremely greater than the frictional entropy generation. Therefore the Bejan number is very close to one for the problems investigated in this research. The same fact was shown by MOGHARIA et al [13] in which for laminar flow inside a circular pipe, the total entropy generation is dominated by the heat transfer entropy generation relative to the frictional irreversibility.
Another interesting outcome of these figures is that addition of nanoparticles reduces the heat transfer entropy generation of nanofluids. The increase of the Reynolds number or nanoparticle volume fraction has a direct effect to decrease the heat transfer entropy generation of flow inside an annulus with a constant radius ratio. But the effect of radius ratio on thermal entropy generation (ST) is somehow complex and for each fluid depends on the value of Re, such that for each Reynolds number and nanoparticle concentration, there is an optimum radius ratio to minimize ST. Generally, the value of ST for nanofluids with volume fraction of 2% and 4% is lowest for an annulus with ri/ro=0.6 over a wide range of investigated Re values. However for pure water at Re=200, the minimum thermal entropy generation corresponds to ri/ro=0.8.

Fig. 22 Heat transfer entropy generation of pure water (φ=0%) for first kind of thermal boundary condition

Fig. 23 Heat transfer entropy generation of water-Al2O3 nanofluid (φ=2%) for first kind of thermal boundary condition
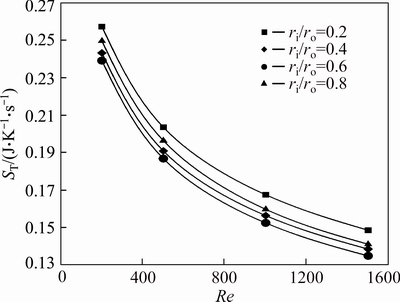
Fig. 24 Heat transfer entropy generation of water-Al2O3 nanofluid (φ=4%) for first kind of thermal boundary condition
Figures 25 and 26 show the relative thermal entropy generation which exhibits the effect of addition of nanoparticle to the pure water on the value of thermal entropy generation. These results are presented as a function of Reynolds number and radius ratio. For ri/ro=0.2, the value of ST is maximum while ST/ST-bf is minimum. It should be noted that the maximum effect of nanoparticle volume fraction on the heat transfer entropy generation is observed for an annulus with ri/ro=0.2, in which the optimum Reynolds numbers are around 700 and 800, for nanofluid slurries with φ=2% and φ=4% respectively. Figure 26 indicates that for volume fraction of 4% and Re>700, ST/ST-bf nearly remains constant.

Fig. 25 Relative heat transfer entropy generation of water-Al2O3 nanofluid (φ=2%) for first kind of thermal boundary condition
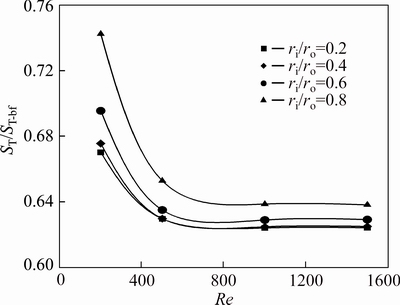
Fig. 26 Relative heat transfer entropy generation of water-Al2O3 nanofluid (φ=4%) for first kind of thermal boundary condition
Figures 27 and 28 show contours of total entropy generation for ri/ro=0.2 at Re=1500 for slurries with φ=2% and φ=4%, respectively. The total entropy generation is higher near the outer wall which temperature gradients are greater. Additionally, comparing these figures indicates that total entropy generation decreases as a consequence of addition of nanoparticles to the base fluid.
In Fig. 29, the total entropy generation of a slurry with φ=4% along an annulus with ri/ro=0.8 and Re=200 is depicted. Obviously in the entrance region of the annulus the entropy generation is smaller than the fully developed region. In addition, the total entropy generation remains constant in the fully developed region and this happens since the temperature profile does not change in this region.

Fig. 27 Total entropy generation of water-Al2O3 nanofluid (φ=2%) for first kind of thermal boundary condition in ri/ro=0.2 and Re=1500
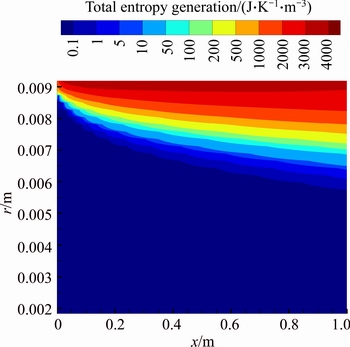
Fig. 28 Total entropy generation of water-Al2O3 nanofluid (φ=4%) for first kind of thermal boundary condition in ri/ro=0.2 and Re=1500
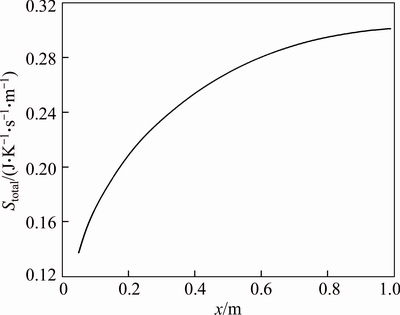
Fig. 29 Total entropy generation of water-Al2O3 nanofluid (φ=4%) in axial direction for the first kind of thermal boundary condition for an annulus with ri/ro=0.8 at Re=200
3.2.3 Second kind of thermal boundary condition
Figures 30-32 show the friction entropy generation (Su) of nanofluids flow inside the annulus for the second kind of thermal boundary condition. The effects of Reynolds number, concentration of nanoparticles and radius ratio on Su is similar to the problem with the first kind of thermal boundary condition. When the inner wall is insulated and the outer wall is exposed to constant heat flux, Su and Su/Su-bf are minimum for ri/ro=0.2 and are maximum in ri/ro=0.8 for all concentrations all over the range of Re investigated in this study. While for the second kind of thermal boundary condition, this manner only can be seen in Su. For this problem, the maximum value of Su/Su-bf is also for the annulus with ri/ro=0.2, while its minimum value depends on the value of Reynolds number and the nanoparticle volume fraction as illustrated in Figs. 33 and 34.

Fig. 30 Friction entropy generation of pure water (φ=0%) for second kind of thermal boundary condition

Fig. 31 Friction entropy generation of water-Al2O3 nanofluid (φ=2%) for second kind of thermal boundary condition

Fig. 32 Friction entropy generation of water-Al2O3 nanofluid (φ=4%) for second kind of thermal boundary condition
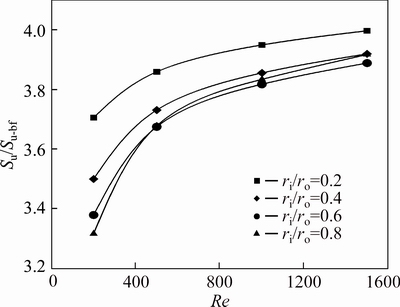
Fig. 33 Relative friction entropy generation of water- Al2O3nanofluid (φ=2%) for second kind of thermal boundary condition

Fig. 34 Relative friction entropy generation of water-Al2O3 nanofluid (φ=4%) for second kind of thermal boundary condition
Figures 35-37 show the thermal entropy generation of water-Al2O3 nanofluids for different annuli as a function of Reynolds number. Similar to the first case, the entropy generation of the second case is also dominated with thermal irreversibility, hence, the Bejan number is very close to one. Obviously, an increase in radius ratio will cause an increase in the heat transfer entropy generation.
The ratio of the heat transfer entropy generation of nanofluids with φ=2% and φ=4% to that of the base fluid are represented in Figs. 38 and 39, respectively. As illustrated in Fig. 38, for the water-Al2O3 nanofluid slurry with φ=2% at Re=200, 500 and 1000, the highest reduction in thermal irreversibility due to addition of nanoparticles is observed for an annulus with ri/ro=0.4. While at Re=1500 the optimum value of ST/ST-bf corresponds to ri/ro=0.8. The interesting point here is that, an annulus with ri/ro=0.8, at Re=200 has maximum value of relative thermal entropy generation while this value at Re=1500 is minimum.
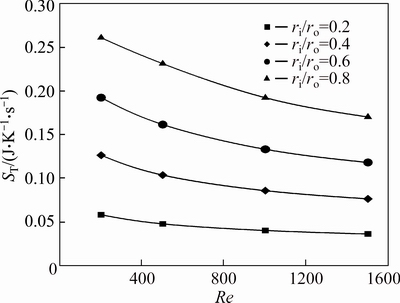
Fig. 35 Heat transfer entropy generation of pure water (φ=0%) for second kind of thermal boundary condition
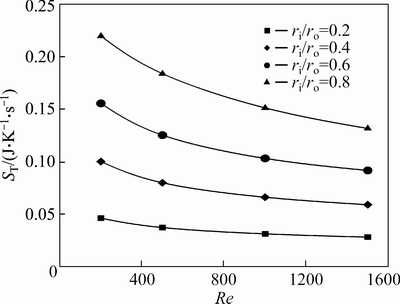
Fig. 36 Heat transfer entropy generation of water-Al2O3 nanofluid (φ=2%) for second kind of thermal boundary condition

Fig. 37 Heat transfer entropy generation of water-Al2O3 nanofluid (φ=4%) for second kind of thermal boundary condition

Fig. 38 Relative heat transfer entropy generation of water-Al2O3 nanofluid (φ=2%) for second kind of thermal boundary condition
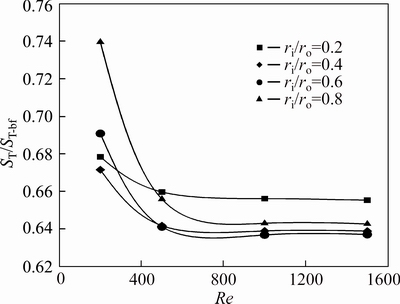
Fig. 39 Relative heat transfer entropy generation of water-Al2O3 nanofluid (φ=4%) for second kind of thermal boundary condition
As depicted in Fig. 39, for the water-Al2O3 nanofluid with φ=4%, at Re=500, 1000 and 1500, the values of ST/ST-bf for annuli with ri/ro=0.8 and 0.2 are respectively minimum and maximum. While at Re=200, the minimum and maximum of ST/ST-bf are respectively connected to radius ratios of 0.4 and 0.8.
Figures 40 and 41 are depicted to show the effect of volume fraction of nanofluid on the total entropy generation. In the same manner as the first case, entropy generation is greater at the vicinity of the walls which are exposed to constant heat flux. Furthermore, addition of nanoparticles can decrease the thickness of the entropy generation layer and leads to lower total entropy generation. Increasing the Reynolds number also has the same effect on the thickness of the entropy generation layer and can cause decline of total entropy generation.
The total entropy generation of water-Al2O3 nanofluid increases in axial direction for ri/ro=0.8 and Re=200, as shown in Fig. 42. Comparing Figs. 29 and 42reveals that at each section of the annulus, entropy generation for the second case is smaller than the first case.

Fig. 40 Total entropy generation of water-Al2O3 nanofluid (φ=2%) for second kind of thermal boundary condition in ri/ro=0.2 and Re=1500
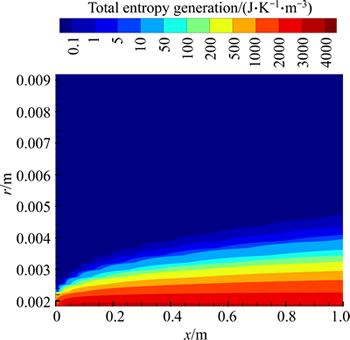
Fig. 41 Total entropy generation of water-Al2O3 nanofluid (φ=4%) for second kind of thermal boundary condition in ri/ro=0.2 and Re=1500

Fig. 42 Total entropy generation of water-Al2O3 nanofluid (φ=4%) in axial direction for second kind of thermal boundary condition for an annulus with ri/ro=0.8 and Re=200
4 Conclusions
In the present work, developing laminar flow of water-Al2O3 nanofluid inside annuli with identical cross sectional area and different radius ratios is simulated numerically in order to investigate the effect of different parameters on the heat transfer and the entropy generation of the flow. The problem is scrutinized for two cases with insulated inner/outer face and constant heat flux on the other face. The analysis of heat transfer enhancement shows that an increase in Reynolds number and the volume fraction of nanoparticles can increase the Nusselt number for the both cases. Generally, it can be concluded that the Nusselt number in higher Reynolds numbers and lower radius ratios of annuli is higher. Relative Nu defined as the ratio of the Nu of nanofluid to that of the pure water, to study the effect of addition of nanoparticles on heat transfer enhancement. For the first case with a constant heat flux on the outer wall of the annulus, the highest relative Nu corresponds to the lowest radius ratio, namely 0.2. However, for the second case, this ratio is 0.4, while the corresponding radius ratio of the lowest heat transfer enhancement depends on the value of Re and the volume fraction of slurry.
Entropy generation of the flow inside an annulus has been computed using two different methods: the differential and the integral approaches. The findings of entropy generation study show that the integral approach is not appropriate for evaluation of entropy generation in annuli and the differential approach have to be employed for our study. Afterwards, the friction and thermal entropy generations computed using the differential approach. With an increase in the Reynolds number and concentration of nanoparticles, it was shown the friction entropy generation increases, while the heat transfer entropy generation decreases. Furthermore, thermal entropy generation is dominant in comparison with the friction irreversibility; hence, the Bejan number is very close to one. In addition, to select a proper radius ratio for an annulus with a specific cross sectional area in order to have minimum total entropy generation at a specific Re, ri/ro=0.2 is the best choice between the investigated radius ratios in this study. However, the optimum radius ratio to minimize the relative entropy generation strongly depends on the thermal boundary conditions, Re and the concentration of nanoparticles.
References
[1] AZARI A. Thermal conductivity modeling of water containing metal oxide nanoparticles [J]. Journal of Central South University, 2015, 22: 1141-1145.
[2] YANG Liu, DU Kai, ZHANG Xiao-song. Influence factors on thermal conductivity of ammonia-water nanofluids [J]. Journal of Central South University, 2012, 19:1622-1628.
[3] HAQUE A K M M, KWON S, KIM J, NOH J, HUH S, CHUNG H, JEONG H. An experimental study on thermal characteristics of nanofluid with graphene and multi-wall carbon nanotubes [J]. Journal of Central South University, 2015, 22: 3202-3210.
[4]  S, PRAMUANJAROENKIJ A. Review of convective heat transfer enhancement with nanofluids [J]. International Journal of Heat and Mass Transfer, 2009, 52: 3187-3196.
S, PRAMUANJAROENKIJ A. Review of convective heat transfer enhancement with nanofluids [J]. International Journal of Heat and Mass Transfer, 2009, 52: 3187-3196.
[5] WUSIMAN Ku-er-ban-jiang, CHUNG H S, NINE M D J, HANDRY A, EOM Y S, KIM J H, JEONG H M. Heat transfer characteristics of nanofluid through circular tube [J]. Journal of Central South University, 2013, 20: 142-148.
[6] ZAIB A, BHATTACHARYYA K, SHAFIE S. Unsteady boundary layer flow and heat transfer over an exponentially shrinking sheet with suction in a copper-water nanofluid [J]. Journal of Central South University, 2015, 22:4856-4863.
[7] ASHRAF M B, HAYAT T, ALSAEDI A, SHEHZAD S A. Convective heat and mass transfer in MHD mixed convection flow of Jeffrey nanofluid over a radially stretching surface with thermal radiation [J]. Journal of Central South University, 2015, 22: 1114-1123.
[8] SHEHZAD S, HUSSAIN T, HAYAT T, RAMZAN M, ALSAEDI A. Boundary layer flow of third grade nanofluid with Newtonian heating and viscous dissipation [J]. Journal of Central South University, 2015, 22: 360-367.
[9] RAFIK S M, KEZZAR M, ADJABI R. Heat transfer of copper/water nanofluid flow through converging-diverging channel [J]. Journal of Central South University, 2016, 23: 484-496.
[10] IZADI M, BEHZADMEHR A, JALALI-VAHIDA D. Numerical study of developing laminar forced convection of a nanofluid in an annulus [J]. International Journal of Thermal Sciences, 2009, 48: 2119-2129.
[11] ALAWIA O A, AZWADI C S N, DAWOOD H K. Natural convection heat transfer in horizontal concentric annulus between outer cylinder and inner flat tube using nanofluid [J]. International Communications in Heat and Mass Transfer, 2014, 57: 65-71.
[12] MATIN M H,
[13] MOGHARIA R M, MUJUMDARB A S, SHARIATA M, TALEBIA F, SAJJADIC S M, AKBARINIAD A. Investigation effect of nanoparticle mean diameter on mixed convection Al2O3-water nanofluid flow in an annulus by two phase mixture model [J]. International Communications in Heat and Mass Transfer, 2013, 49: 25-35.
[14] YANG C, LI W, NAKAYAMA A. Convective heat transfer of nanofluids in a concentric annulus [J]. International Journal of Thermal Sciences, 2013, 71: 249-257.
[15] DAWOODA H K, MOHAMMED H A, AZWADI C S N, MUNISAMY K M, WAHID M A. Forced, natural and mixed-convection heat transfer and fluid flow in annulus: A review [J]. International Communications in Heat and Mass Transfer, 2015, 62: 45-57.
[16] BEJAN A. Entropy generation minimization: The method of thermodynamic optimization of finite-size systems and finite-time processes [M]. CRC press, 1995.
[17] BIANCO V, NARDINI S, MANCA O. Enhancement of heat transfer and entropy generation analysis of nanofluids turbulent convection flow in square section tubes [J]. Nanoscale Research Letters, 2011, 6: 252.
[18] BIANCOA V, MANCAB O, NARDINI S. Entropy generation analysis of turbulent convection flow of Al2O3–water nanofluid in a circular tube subjected to constant wall heat flux [J]. Energy Conversion and Management, 2014, 77: 306-314.
[19] LEONG K Y, SAIDUR R, MAHLIA T M I, YAU Y H. Entropy generation analysis of nanofluid flow in a circular tube subjected to constant wall temperature [J]. International Communications in Heat and Mass Transfer, 2012, 39: 1169-1175.
[20] MOGHADDAMI M, MOHAMMADZADE A, ALEM V E S. Second law analysis of nanofluid flow [J]. Energy Conversion and Management, 2011, 52: 1397-1405.
[21] MOGHADDAMI M, SHAHIDI S, SIAVASHI M. Entropy generation analysis of nanofluid flow in turbulent and laminar regimes [J]. Journal of Computational and Theoretical Nanoscience, 2012, 9: 1586-1595.
[22] YARMAND H, AHMADI G, GHAREHKHANI S, NEWAZ K S, REZA S M, SADAT A M, BAKAR M A. Entropy generation during turbulent flow of zirconia-water and other nanofluids in a square cross section tube with a constant heat flux [J]. Entropy, 2014, 16: 6116-6132.
[23] MAHIAN O, KIANIFAR A, KLEINSTREUER C, AL-NIMRC M A, POPD I, SAHINE A Z, WONGWISES S. A review of entropy generation in nanofluid flow [J]. International Journal of Heat and Mass Transfer, 2013, 65: 514-532.
[24] KUCUK H. Numerical analysis of entropy generation in concentric curved annular ducts [J]. Journal of Mechanical Science and Technology, 2010, 24: 1927-1937.
[25] WU Shuang-ying, CHEN Su-jun, XIAO Lan, LI You-rong. Numerical investigation on developing laminar forced convective heat transfer and entropy generation in an annular helicoidal tube [J]. Journal of Mechanical Science and Technology, 2011, 25: 1439-1447.
[26] MAHMUD S, FRASER A R. Analysis of entropy generation inside concentric cylindrical annuli with relative rotation [J]. International Journal of Thermal Sciences, 2003, 42: 513-521.
[27] HADDAD O M, ALKAM M K, KHASAWNEH M T. Entropy generation due to laminar forced convection in the entrance region of a concentric annulus [J]. Energy, 2004, 29: 35-55.
[28] SIAVASHI M, BAHRAMI H R T, SAFFARI H. Numerical investigation of porous rib arrangement on heat transfer and entropy generation of nanofluid flow in an annulus using a two-phase mixture model [J]. Numerical Heat Transfer, Part A: Applications, 2017, 71: 1174-1196.
[29] SIAVASHI M, BAHRAMI H R T, SAFFARI H. Numerical investigation of flow characteristics, heat transfer and entropy generation of nanofluid flow inside an annular pipe partially or completely filled with porous media using two-phase mixture model [J]. Energy, 2015, 93, Part 2: 2451-2466.
[30] SIAVASHI M, JAMALI M. Heat transfer and entropy generation analysis of turbulent flow of TiO2-water nanofluid inside annuli with different radius ratios using two-phase mixture model [J]. Applied Thermal Engineering, 2016, 100: 1149-1160.
[31] GHASEMI K, SIAVASHI M. Lattice Boltzmann numerical simulation and entropy generation analysis of natural convection of nanofluid in a porous cavity with different linear temperature distributions on side walls [J]. Journal of Molecular Liquids, 2017, 233: 415-430.
[32] GHASEMI K, SIAVASHI M. MHD nanofluid free convection and entropy generation in porous enclosures with different conductivity ratios [J]. Journal of Magnetism and Magnetic Materials, 2017, 442: 474–490.
[33] SIAVASHI M, BORDBAR V, RAHNAMA P. Heat transfer and entropy generation study of non-Darcy double-diffusive natural convection in inclined porous enclosures with different source configurations [J]. Applied Thermal Engineering, 2017, 110: 1462–1475.
[34] TOOSI M H, SIAVASHI M. Two-phase mixture numerical simulation of natural convection of nanofluid flow in a cavity partially filled with porous media to enhance heat transfer [J]. Journal of Molecular Liquids, 2017, 238: 553-569.
[35] BEJAN A. Second law analysis in heat transfer [J]. Energy, 1980, 5: 720-732.
[36]  S, TAM N C, GALANISB N, ROY G. Heat transfer behaviours of nanofluids in a uniformly heated tube [J]. Superlattice Microst, 2004, 35: 543-557.
S, TAM N C, GALANISB N, ROY G. Heat transfer behaviours of nanofluids in a uniformly heated tube [J]. Superlattice Microst, 2004, 35: 543-557.
[37] KHANAFERA K, VAFAI K. A critical synthesis of thermophysical characteristics of nanofluids [J]. International Journal of Heat and Mass Transfer, 2011, 54: 4410-4428.
[38] PAK B C, CHO Y I. Hydrodynamic and heat transfer study of dispersed fluids with submicron metallic oxide particles [J]. Experimental Heat Transfer, 1998, 11: 151-170.
[39] XUANA Y, ROETZEL W. Conceptions for heat transfer correlation of nanofluids [J]. International Journal of Heat and Mass Transfer, 2000, 43: 3701-3707.
[40] KOO J, KLEINSTREUER C. A new thermal conductivity model for nanofluids [J]. Journal of Nanoparticle Research, 2004, 6: 577-588.
[41] XUAN Yi-min, LI Qiang. Heat transfer enhancement of nanofluids [J]. International Journal of Heat and Fluid Flow, 2000, 21: 58-64.
[42] HAGEN K D. Heat transfer with applications [M]. Prentice Hall, 1999.
[43] RAISEE M, MOGHADDAMI M. Numerical investigation of laminar forced convection of nanofluids through circular pipes [J]. Journal of Enhanced Heat Transfer, 2008, 15: 335-350.
[44] DAS S K, PUTRA N, THIESEN P, ROETZEL W. Temperature dependence of thermal conductivity enhancement for nanofluids [J]. Journal of Heat Transfer, 2003, 125: 567-574.
[45] REA U, MCKRELL T, HU Lin-wen, BUONGIORNO J. Laminar convective heat transfer and viscous pressure loss of alumina–water and zirconia–water nanofluids [J]. International Journal of Heat and Mass Transfer, 2009, 52: 2042-2048.
[46] PATANKAR S. Numerical heat transfer and fluid flow [M]. Taylor & Francis, 1980.
[47] ROHSENOW W M, HARTNETT J P, CHO Y I. Handbook of heat transfer [M]. McGraw-Hill, 1998.
(Edited by YANG Bing)
Cite this article as: Siavashi Majid, Jamali Mohammad. Optimal selection of annulus radius ratio to enhance heat transfer with minimum entropy generation in developing laminar forced convection of water-Al2O3 nanofluid flow [J]. Journal of Central South University, 2017, 24(8): 1850-1865. DOI: https://doi.org/10.1007/s11771-017-3593-7.
Received date: 2016-03-04; Accepted date: 2016-09-30
Corresponding author: Siavashi Majid, Assistant Professor, PhD; Tel: +98-21-77240391; E-mail: msiavashi@iust.ac.ir

