文章编号：1004-0609(2008)01-0126-06

Ti-Nb合金β结构稳定性和弹性性质

姚  强，邢  辉，郭文渊，孙  坚

(上海交通大学 材料科学与工程学院，上海 200240)

摘  要：采用基于密度函数理论的缀加平面波加局域轨道(APW+lo)方法和超晶胞方法对Nb含量为6.25%~37.5%Nb(摩尔分数)的Ti-Nb二元合金的能量、电子结构以及弹性性质进行了理论计算，研究Nb含量对Ti-Nb合金的β结构稳定性和弹性性质的影响。结果表明，随着Nb含量的升高，Ti-Nb合金的β结构稳定性提高，正方剪切常数C′以及弹性模量K、E和G呈单调增加。当Nb含量为9.87%时，正方剪切常数大于并接近于零，此时Ti-Nb合金的β结构稳定性最低，并具有最低的弹性模量。

关键词：钛铌合金；结构稳定性；弹性性质；第一性原理

中图分类号：TG146.2　　     文献标识码：A

β phase stability and elastic property of Ti-Nb alloys

YAO Qiang, XING Hui, GUO Wen-yuan, SUN Jian

(School of Materials Science and Engineering, Shanghai Jiao Tong University, Shanghai 200240, China)

Abstract: The energetic, electronic structure and elastic property of Ti-Nb binary alloys with Nb contents ranging from 6.25% to 37.5% (mole fraction) were calculated using the method of supercell and augmented plane waves plus local orbitals within generalized gradient approximation. Based on the calculated results, the influences of Nb content on the β phase stability and elastic property of Ti-Nb alloys were investigated. The results show that the β phase stability, tetragonal shear constant C′, bulk modulus, elastic modulus and shear modulus of Ti-Nb alloys increase monotonously with increasing Nb content. when the Nb content is 9.87%, the tetragonal shear constant C′ of Ti-Nb alloy reaches nearly zero from positive, and meanwhile the alloy achieves the lowest phase stability and the lowest elastic modulus.

Key words: Ti-Nb alloy; phase stability; elastic property; first-principles

钛合金因具有低密度、高强度、耐腐蚀和优良的生物相容性等特点而被广泛应用于各种工业以及生物医学工程领域^[1]。目前医用的钛合金材料主要为Ti-6Al-4V合金，该合金弹性模量高(约110 GPa)且所含的Al和V均为生物毒性元素，长期使用会对人体造成损害^[2]。最近研究表明，添加部分对生物无毒性过渡族元素(如Nb，Mo和Ta等)的β型钛合金，具有低弹性模量、超弹性以及形状记忆效应等特性，作为新型生物医用材料有很广阔的应用前景，因而引起人们的广泛关注^[3?9]。目前应用电子理论针对这类β型钛合金的材料设计问题已经成为研究的热点。例如KURODA等^[10]采用基于DV-Xα Cluster方法的d电子理论对多种β型钛合金进行了系统的研究，研究表明钛合金的键序(Bo)和d电子轨道能级(Md)等重要参数与钛合金的组织结构和弹性性质存在很好的关联性，并由此进行低模量钛合金设计。但这种理论没有能够给出钛合金上述电子结构参数与其性质之间关联的物理本质。最近IKEHATA等^[11]采用超软赝势方法对Ti_1?xX_x合金(x＝0，0.25，0.50，0.75，1，X=V，Nb，Ta，Mo，W)的弹性性质进行了理论计算，研究表明刚性能带模型(Rigid band model)对于Ti-X 合金成立，并由此推导出β结构Ti-X合金价电子浓度与其弹性稳定性的关系。

本文作者采用基于密度函数理论的缀加平面波加局部轨道方法和广义梯度近似，以及超晶胞方法对Nb含量为6.25%~37.5%(摩尔分数)的Ti-Nb合金的能量和弹性性质以及电子结构进行理论计算，系统研究Nb含量对Ti-Nb合金β结构稳定性以及弹性性质的作用规律，为低弹性模量的Ti-Nb合金设计提供理论依据。

1  计算方法

采用基于密度函数理论(DFT)的缀加平面波加局域轨道(APW＋lo)方法，并采用广义梯度近似(GGA)来处理交换关联能，该方法的优点是在获得高计算精度的同时可以得到更快的收敛速度^[12]。平面波的截断点(R_mtK_max)的取值为7.0；经测试k取1 000点。采用四面体方法对布理渊区进行积分^[13]。对Ti-Nb合金进行计算时，Ti和Nb的Muffin-Tin半径均取2.3 a.u.，自洽循环计算的收敛准则为0.000 1 Ry。本研究建立    2×2×2的体心立方结构β-Ti超晶胞，该超晶胞中含有16个原子。采用x(x=1~6)个Nb原子去分别置换立方β结构超晶胞中的Ti原子，此时Ti-Nb合金的名义分子式为Ti_16?xNb_x(Nb元素的摩尔分数为6.25%~ 37.5%)。

2  计算结果与讨论

2.1  晶格常数和内聚能

首先对不同Nb含量的各超晶胞的晶格常数进行了优化，得到的平衡晶格常数如图1所示。从图 中可以看出随着Nb含量的增加，相应β结构晶胞的晶格常数基本以线性关系逐渐增大，这是由于Nb原子的原子半径大于Ti原子的所造成的。为了研究Nb含量与β结构Ti-Nb合金的结构稳定性之间的关系，需进行内聚能E_coh计算。内聚能计算式如下：

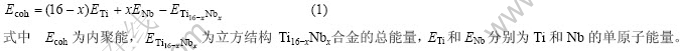
不同Nb含量的Ti-Nb合金的内聚能计算结果如图2所示。可以看出，随着Nb含量的增加，合金的内聚能以线性关系逐渐增大，这说明Nb元素的添加能提高β结构的Ti-Nb合金的稳定性。

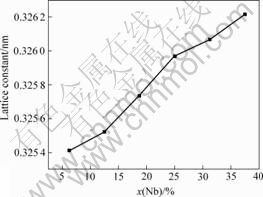
图1  Ti-Nb合金晶格常数与Nb含量的关系

Fig.1  Relationship between lattice constants and Nb content

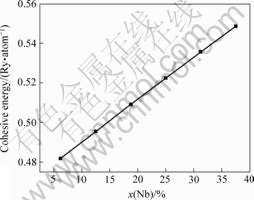
图2  E_coh与Nb含量的关系

Fig.2  Relationship between E_coh and Nb content

2.2  态密度

为了揭示添加Nb元素对Ti-Nb合金β结构稳定性影响的物理本质，本研究计算了β结构Ti_16?xNb_x合金的态密度分布(DOS)。图3所示为β结构Ti_16?xNb_x(x=2，4，6)态密度分布的计算结果，其中虚线表示费米能的位置。由图3可以看出，Ti₁₄Nb₂，Ti₁₂Nb₄和Ti₁₀Nb₆ 三者态密度分布图的峰形十分相似，且态密度分布图中均存在一个能区分出态密度分布中的低能成键态和高能反键态区域的峰谷，而费米能级均处于成键态区域，导致了费米能级处态密度N(E_F)值相对比较高，这也说明了Ti-Nb合金β结构的稳定性相对较低。随着Nb含量的增加，Ti_16?xNb_x(x=2, 4, 6)合金态密度分布图中费米能所处的位置逐渐向峰谷方向移动，成键峰则逐渐向低能方向移动，这说明随着Nb元素含量的增加，TiNb合金β结构的稳定性逐渐提高，这与以上内聚能计算结果是自洽的。

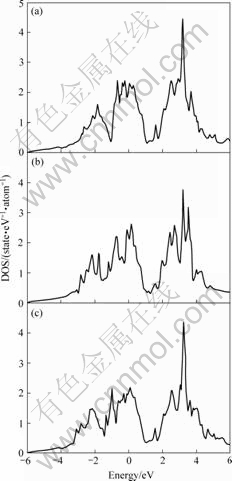
图3  Ti_16?xNb_x (x=2,4,6) 的态密度计算结果

Fig.3  Densities of Ti_16?xNb_x states (x=2, 4, 6): (a) Ti₁₄Nb₂;   (b) Ti₁₂Nb₄; (c) Ti₁₀Nb₆

2.3  弹性性质

β立方结构的Ti-Nb合金存在3个独立的弹性常数即C₁₁、C₁₂和C₄₄。为了计算β结构Ti_16?xNb_x合金的弹性常数，可先对晶胞进行不同的弹性变形然后算出变形后的能量，并通过此能量与未变形晶胞的能量差，求出弹性应变能，进而得到弹性常数。弹性应变能计算式如下：

首先对晶胞进行等体积的正应变变形，此时应变量e₁=?e₂=e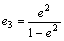，，应变张量ε为

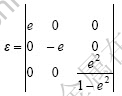
根据此应变张量，得到经正应变变形后的弹性应变能

另外，体模量(可以通过晶胞的体积优化过程得到)和弹性常数存在以下关系：

因此，联立式(3)和式(4)即可计算出C₁₁和C₁₂。

其次，对原始晶胞进行等体积的切应变变形，此时应变量e₆=e，e₃=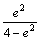，应变张量ε为

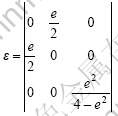
根据此应变张量，得到经切应变变形后的弹性应变能

采用上述方法计算得到的弹性常数可进一步计算出Ti-Nb合金的切变模量和弹性模量。在多晶材料弹性模量的理论计算方面，HILL通过极值原理证明Voigt和Reuss模型的计算结果是弹性常数的上下限，Hill模型则将Voigt和Reuss模型的计算结果取一个简单的算术平均^[14]，其切变模量为

在Voigt模型中，切变模量G_V为

而在Reuss模型中，切变模量G_R为

式中  S_ij为C_ij的逆矩阵。弹性模量的计算式如下：

不同Nb含量的Ti-Nb合金的弹性常数和弹性模量的计算结果分别如图4~7所示。由图可知，随着Nb含量的增加，弹性常数C₁₁和C₁₂呈单调增加趋势，但弹性常数C₄₄则呈下降趋势。Ti-Nb合金的体模量K、切变模量G和弹性模量E均随着Nb含量的增加呈单调增加趋势。根据Born弹性稳定性准则，立方结构晶体的弹性常数必须同时满足：

立方结构晶体才可以存在^[15]。因此，正方剪切常数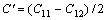可以反映其晶体结构的稳定性，Ti-Nb合金的正方剪切常数与Nb含量之间的关系如图8所示。由图8可以看出随着Nb含量的增加，Ti-Nb合金的正方剪切常数也呈单调增加趋势。这从晶体弹性稳定性角度说明了随着Nb元素含量的增加，Ti-Nb合金β结构的稳定性逐渐提高，这与以上能量以及电子结构的计算结果也是一致的。当Nb含量为6.25%时，正方剪切常数C′＜0，因此Ti₁₅Nb₁合金不能以β立方结构存在，而只能以六方结构或其它亚稳结构的形式存在；从图8可以推出当Nb含量大于9.87%时，正方剪切常数C′＞0，此时Ti-Nb合金满足Born弹性稳定性准则，即理论上该合金可以β结构形式存在。此时Ti-Nb合金的电子浓度e/a为4.10。最近LI等^[16]采用虚晶近似计算方法研究β结构Ti-V二元合金的力学性质时同样发现，当合金的电子浓度e/a大于4.10时β结构的Ti-V合金才能够稳定存在。IKEHATA   等^[11]采用超软赝势方法并结合刚性能带模型近似方法推导出稳定β结构Ti-X合金的临界价电子浓度(e/a)为4.20。这说明合金的电子浓度e/a决定了β结构Ti合金的稳定性，即当e/a大于4.10时β结构Ti合金从晶体弹性稳定性意义上是能够存在的。但在热力学意义上该成分Ti-Nb合金仍处于亚稳定状态，由相图分析可知Nb含量为40%的Ti-Nb合金在热力学上才是稳定的。LEE等^[17]采用X射线衍射方法研究了一系列不同成分的Ti-Nb合金快冷组织后发现，当Nb含量在8.33%时Ti-Nb合金中仅观察到六方结构或正交结构的马氏体亚稳组织；Nb含量为16.35%时合金中出现β以及正交结构的马氏体组织；当Nb含量超过21.72%时合金为单一β结构。因此，在实际合金中β结构最终能否稳定存在取决于合金中不同结构亚稳相的相对稳定性大小。从上述研究结果分析可以看出当正方剪切常数大于并接近于零时，Ti-Nb合金β结构稳定性最低，此时β结构Ti-Nb合金具有最低的弹性模量。在实践中进行低弹性模量Ti-Nb合金设计时，还需进一步进行合金化来抑制马氏体转变或其它亚稳相转变，以获得具有单一β组织的低弹性模量的Ti-Nb合金。

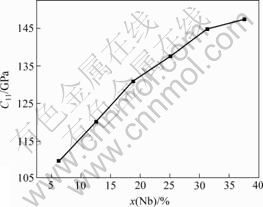
图4  弹性常数C₁₁与Nb含量的关系

Fig.4  Relationship between elastic constant C₁₁ and Nb content

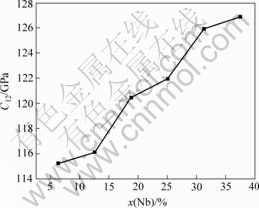
图5  弹性常数C₁₂与Nb含量的关系

Fig.5  Relationship between elastic constant C₁₂ and Nb content

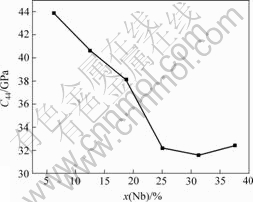
图6  弹性常数C₄₄与Nb含量的关系

Fig.6  Relationship between elastic constant C₄₄ and Nb content

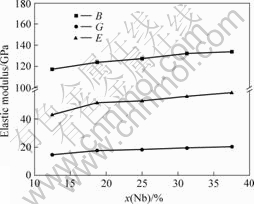
图7  弹性模量与Nb含量的关系

Fig.7  Relationships between elastic modulus and Nb content

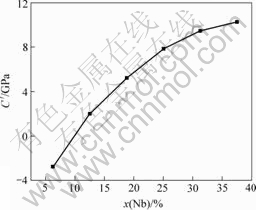
图8  正方剪切常数C′与Nb含量的关系

Fig.8  Relationship between tetragonal shear constant C′ and Nb content

3  结论

1) 理论计算结果表明，随着Nb含量的升高，Ti-Nb合金的β结构稳定性提高，弹性常数C₁₁、C₁₂、正方剪切常数C?以及弹性模量K，E和G均呈单调增加，而弹性常数C₄₄呈下降趋势。

2) 当Nb含量为9.87%(电子浓度e/a为4.10)，正方剪切常数大于并接近于零，此时Ti-Nb合金的β结构稳定性最低，并具有最低的弹性模量。

REFERENCES

[1] LONG M, RACK H J. Titanium alloys in total joint replacement-A materials science perspective[J]. Biomaterials, 1998, 19: 1621?1639.

[2] GEETHA M, SINGH A K, MURALEEDHARAN K, GOGIA A K, ASOKAMANI R. Effect of thermomechanical processing on microstructure of a Ti-13Nb-13Zr alloy[J]. Journal of Alloys and Compounds,2001, 329(1/2): 264?271.

[3] KIM H Y, IKEHARA Y, KIM J I, HOSODA H, MIYAZAKI S. Martensitic transformation, shape memory effect and superelasticity of Ti-Nb binary alloys[J]. Acta Materialia, 2006, 54: 2419?2429.

[4] MIYAZAKI S, KIM H Y, HOSODA H. Development and characterization of Ni-free Ti-base shape memory and superelastic alloys[J]. Mater Sci Eng A, 2006, 438/440: 18?24.

[5] KIM H Y, SASAKI T, OKUTSU K, KIM J I, INAMURA T, HOSODA H, MIYAZAKI S. Texture and shape memory behavior of Ti-22Nb-6Ta alloy[J]. Acta Materialia, 2006, 54: 423?433.

[6] ZHANG L C, ZHOU T, ALPAY S P, AINDOW M. Origin of pseudoelastic behavior in Ti-Mo-based alloys[J]. Applied Physics Letters, 2005, 87: 241909.

[7] 张新平, 于思荣, 何镇明, 韩秋华. 新型Ti-Fe-Mo-Mn-Nb-Zr系钛合金的力学性能[J]. 中国有色金属学报, 2002, 12(S1): 78?82.
ZHANG Xin-ping, YU Si-rong, HE Zhen-ming, HAN Qiu-hua. Mechanical properties of new type Ti-Fe-Mo-Mn-Nb-Zr titanium alloy[J]. The Chinese Journal of Nonferrous Metals, 2002, 12(S1): 78?82.

[8] ZHOU Y L, NIINOMI M, AKAHORI T. Effects of Ta content on Young’s modulus and tensile properties of binary Ti-Ta alloys for biomedical applications[J]. Mater Sci Eng A, 2004, 371: 283?290.

[9] ZHOU T, AINDOW M, ALPAY S P, BLACKBURN M J, WU M H. Pseudo-elastic deformation behavior in a Ti/Mo-based alloy[J]. Scripta Materialia, 2004, 50: 343?348.

[10] KURODA D, NIINOMI M, MORINAGA M, KATO Y, YASHIRO T. Design and mechanical properties of new β type titanium alloys for implant materials[J]. Mater Sci Eng A, 1998, 243:244-249.

[11] IKEHATA H, NAGASAKO N, FURUTA T, FUKUMOTO A, MIWA K, SAITO T. First-principles calculations for development of low elastic modulus Ti alloys[J]. Physical Review B, 2004, 70: 174113.

[12] SCHWARZ K, BLAHA P, MADSEN G K H. Electronic structure calculations of solids using the WIEN2k package for material sciences[J].Computer Physics Communications, 2002,147(1/2): 71?76.

[13] BL?CHL P E, JEPSEN O, ANDERSEN O K. Improved tetrahedron method for Brillouin-zone integrations[J]. Physical Review B, 1994, 49(23): 16223?16233.

[14] ANDERSON O L. A simplified method for calculating the Debye temperature from elastic constants[J]. The Journal of Physics and Chemistry of Solids, 1963, 24: 909?917.

[15] BORN M, HUANG K. Dynamical theory of crystal lattices[M]. Oxford: Clarendon Press, 1954: 141.

[16] LI T S, MORRIS J W, NAGASAKO N, KURAMOTO S, CHRZAN D C. Ideal engineering alloys[J]. Physical Review Letters, 2007, 98: 105503.

[17] LEE C M, JU C P, CHERN LIN J H. Structure-property relationship of cast Ti-Nb alloys[J]. Journal of Oral Rehabilitation, 2002, 29: 314?322.

基金项目：国家自然科学基金资助项目(50571063)；上海市重点基础资助项目(04JC14054)

收稿日期：2007-05-08；修订日期：2007-09-12

通讯作者：孙  坚，教授；电话：021-54745593；E-mail: jsun@sjtu.edu.cn

(编辑 陈爱华)