DOI: 10.11817/j.issn.1672-7207.2016.03.032
下部脱胶界面圆夹杂的弹性动力学反平面分析
齐辉1,高春1, 2,周亚东1, 3,潘向南1,蔡立明1
(1. 哈尔滨工程大学 航天与建筑工程学院,黑龙江 哈尔滨,150001;
2. 哈尔滨学院 土木工程系,黑龙江 哈尔滨,150086;
3. 济宁市建筑设计研究院,山东 济宁,272000)
摘要:针对下部脱胶的界面圆柱夹杂对SH波的散射问题进行稳态研究。按照“分割”和“契合”思想,采用复变函数法、Green函数法与多极坐标法相结合实现边值问题的求解。首先,分别求解沿双相介质交界面剖分的上、下半空间的Green函数;其次,在界面上附加未知力系,将上、下半空间契合在一起,按交界面上的位移和应力的连续条件构造定解积分方程组;再次,采用直接离散法求解积分方程组,反推得到位移和应力场的表达式;最后,按应力场的表达式求得界面夹杂边沿的动应力集中因子。数值研究2个界面脱胶夹杂之间的相互作用,给出夹杂边沿动应力集中因子的分布情况。研究结果表明,界面脱胶夹杂之间的相互影响十分显著。
关键词:SH波散射;Green函数;界面夹杂;脱胶;动应力集中
中图分类号:O343.1;P315.3 文献标志码:A 文章编号:1672-7207(2016)03-0959-08
Anti-plane analysis for steady state elastodynamics of interfacial debonding-bottomed circular inclusions
QI Hui1, GAO Chun1, 2, ZHOU Yadong1, 3, PAN Xiangnan1, CAI Liming1
(1. College of Aerospace and Civil Engineering, Harbin Engineering University, Harbin 150001, China;
2. Department of Civil Engineering, Harbin University, Harbin 150086, China;
3. Jining Institute of Building Design and Research, Jining 272000, China)
Abstract: SH wave scattering problem of interfacial debonding-bottomed circular inclusions was steadily analyzed, by using “split” and “conjunction”, with complex function method, Green function method, and multi-polar coordinate method. Firstly, Green functions of two split half spaces were constructed, respectively. Secondly, the determined integral equations of unknown forces along conjunctive interface were expressed through the "conjunction" condition which claims displacement and stress continuous on the conjunctive interface. Thirdly, displacement and stress fields were presented by using solved integral equations with direct discrete method. Lastly, dynamic stress concentrations factor around the interfacial inclusion was formulated with expressions of stress fields. Numerical examples were calculated to study the interaction of two interfacial debonding-bottomed circular inclusions, and distributions of dynamic stress concentrations factor around inclusion were displayed. The results show that there are significant effects between interfacial debonding inclusions.
Key words: SH wave scattering; Green function; interfacial inclusion; debond; dynamic stress concentration
弹性波的散射问题一直备受科学家和工程师的关注,随着在无损检测、能源勘探、地震工程等领域的广泛应用,关于弹性波散射的研究也越来越多。早期,对弹性波散射的研究主要集中在全空间中单个简单异质体,例如圆柱空洞或夹杂、椭圆柱孔洞或夹杂、球形孔洞或夹杂等[1]。作为最简单的弹性波的形式,SH波的传播和散射问题得到了更系统和全面的研究。刘殿魁等[2]创建了SH波二维散射的复变函数论方法,将弹性静力学的保角变换推广到弹性动力学,从形式上解决了全空间中任意形状柱体的反平面散射问题。考虑界面的反平面散射问题较全空间更复杂,TRIFUNAC等[3-4]按照波函数展开法和镜像法研究了半空间中的散射问题;袁晓铭等[5]研究了半空间中圆柱形的凹陷、夹杂和凸起对SH波的稳态散射;杨在林等[6-7]研究了半空间中椭圆形孔洞、夹杂和裂纹对稳态波的反平面散射。界面夹杂对SH波的散射问题是一类更为复杂的弹性动力学界面问题,刘殿魁等[8]运用Green函数方法,研究了界面圆柱形孔洞和夹杂的反平面稳态散射;汪越胜等[9]用积分方程的方法讨论了局部脱胶情况下的散射问题;齐辉等[10-17]按照“契合”思想结合Green函数和积分方程的方法系统地研究了稳态SH波的弹性动力学界面问题。本文作者按“分割”与“契合”的思想,通过Green函数法、复变函数法与多极坐标法相结合的方法,研究全空间中含下部脱胶界面夹杂对平面SH波的稳态响应,给出圆柱夹杂边沿的动应力集中因子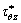 的分布情况。
的分布情况。
1 模型的描述
采用“分割”的思想,将全空间模型分割成上、下2个半空间模型,上半空间为含半圆柱形凸起的半空间,下半空间为含半圆形凹陷的半空间。全空间模型如图1所示。图中:介质I为下半空间;介质Ⅱ为上半空间;介质Ⅲ为界面圆柱夹杂;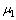 ,
,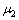 和
和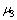 分别为3种介质的剪切弹性模量;
分别为3种介质的剪切弹性模量;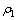 ,
,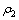 和
和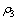 分别为3种介质的质量密度;Oj为圆柱夹杂的圆心;dj为第j个半圆形凹陷的圆心坐标;Rj为半径,坐标系XjOjYj是以Oj为原点建立的局部坐标系,坐标系XOY是以某个局部坐标系为基准建立的全局坐标系;
分别为3种介质的质量密度;Oj为圆柱夹杂的圆心;dj为第j个半圆形凹陷的圆心坐标;Rj为半径,坐标系XjOjYj是以Oj为原点建立的局部坐标系,坐标系XOY是以某个局部坐标系为基准建立的全局坐标系;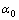 为稳态SH平面波的入射角;S,C为边界。
为稳态SH平面波的入射角;S,C为边界。
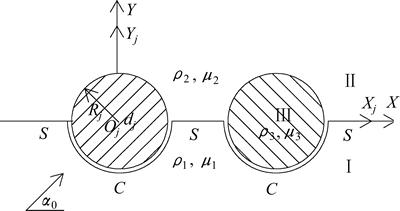
图1 全空间模型
Fig. 1 Whole space model
2 Green函数的构造
2.1 上半空间的Green函数
将上半空间模型沿公共边界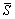 (或
(或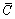 )分割成介质Ⅱ与界面圆柱夹杂Ⅲ 2部分,其示意图如图2和图3所示。
)分割成介质Ⅱ与界面圆柱夹杂Ⅲ 2部分,其示意图如图2和图3所示。
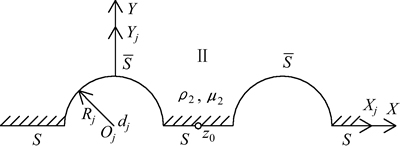
图2 格林函数的上半空间模型
Fig. 2 Upper half space model of green function
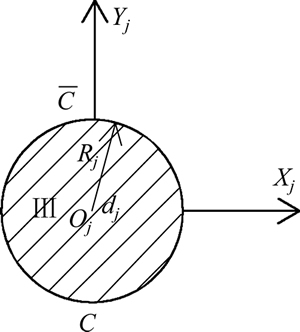
图3 界面圆形夹杂模型
Fig. 3 Interfacial circular inclusion model
半空间作用线源荷载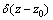 时,入射波
时,入射波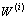 可以表示为
可以表示为
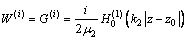 (1)
(1)
满足上半空间界面上应力自由的散射波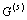 的表达式为
的表达式为
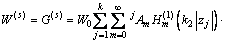
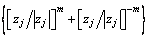 (2)
(2)
其中: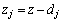 ;W0为位移幅值,一般取1.0;k为半圆形凹陷的数量。在区域Ⅱ内G2可以表示为
;W0为位移幅值,一般取1.0;k为半圆形凹陷的数量。在区域Ⅱ内G2可以表示为
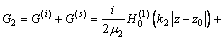
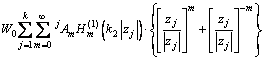 (3)
(3)
如图3所示,夹杂Ⅲ内的驻波满足边界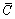 上应力任意与边界C上应力自由,这个边界条件在局部坐标系
上应力任意与边界C上应力自由,这个边界条件在局部坐标系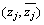 下可以表示为
下可以表示为
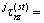
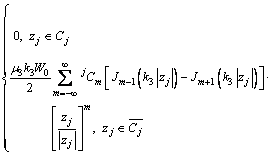 (4)
(4)
其解为
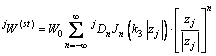 (5)
(5)
式(4)在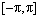 内展开成Fourier级数的形式如下式所示:
内展开成Fourier级数的形式如下式所示:
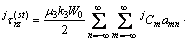
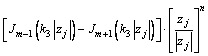 (6)
(6)
其中:
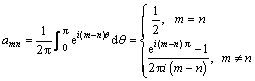 (7)
(7)
当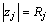 时,将由式(5)求得的应力表达式与式(4)进行对应,得到:
时,将由式(5)求得的应力表达式与式(4)进行对应,得到:
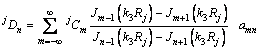 (8)
(8)
将式(8)代入式(5)中,得到驻波解的具体表达式为
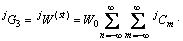
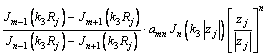 (9)
(9)
介质Ⅱ与夹杂Ⅲ中Green函数的表达式含有2k个未知数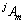 和
和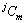 ,对上半空间Green函数的求解即对未知数
,对上半空间Green函数的求解即对未知数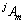 和
和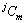 的求解,采用“契合”的思想解答,将夹杂Ⅲ与区域Ⅱ契合在一起,利用契合边界
的求解,采用“契合”的思想解答,将夹杂Ⅲ与区域Ⅱ契合在一起,利用契合边界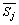 上位移、应力的连续性条件,构造以下方程组:
上位移、应力的连续性条件,构造以下方程组:
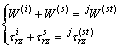 ,j=1, 2, …, k (10)
,j=1, 2, …, k (10)
按多极坐标的方法求解,将全局坐标系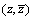 用局部坐标系
用局部坐标系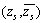 表达,将按全局坐标
表达,将按全局坐标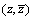 表示的位移和应力方程转化为局部坐标
表示的位移和应力方程转化为局部坐标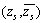 的方程。定义
的方程。定义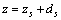 ,
,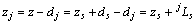 ,则
,则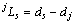 ,且
,且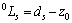 ,相应的位移和应力表达式变为
,相应的位移和应力表达式变为
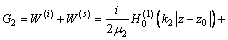
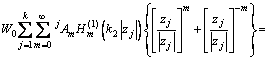
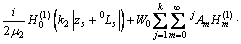
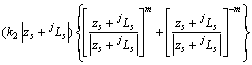 (11)
(11)
当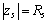 时,边界条件可以表示为
时,边界条件可以表示为
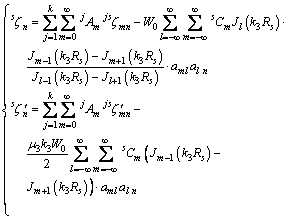 (12)
(12)
这就是求解未知系数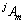 和
和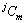 的无穷代数方程组,其中:
的无穷代数方程组,其中:
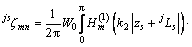
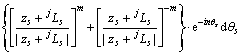 ;
;
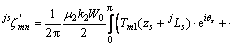
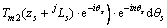 ,
,
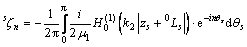 ;
;
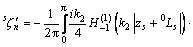
 ;
;
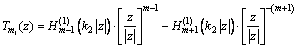 ;
;
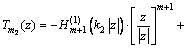
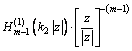 。
。
求解得到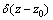 作用下介质Ⅱ的Green函数
作用下介质Ⅱ的Green函数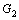 和界面夹杂的Green函数
和界面夹杂的Green函数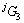 :
:
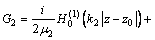
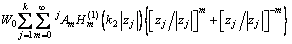 (13)
(13)
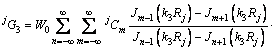
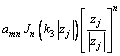 (14)
(14)
2.2 下半空间的Green函数
下半空间的模型如图4所示。
按同样的方法构造下半空间的Green函数,
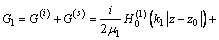
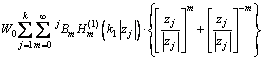 (15)
(15)
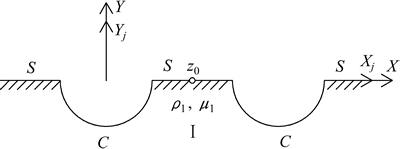
图4 Green函数的下半空间模型
Fig. 4 Lower half space model of Green function
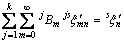 (16)
(16)
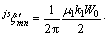
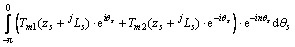 (17)
(17)
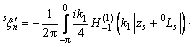
 (18)
(18)
其中: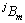 为散射波内的未知系数:
为散射波内的未知系数: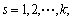
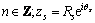 。
。
3 稳态SH波的入射
稳态SH波的全空间模型如图5所示,稳态SH波以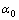 角入射,产生的入射波、反射波、折射波和散射波构成了介质中的总波场。入射波
角入射,产生的入射波、反射波、折射波和散射波构成了介质中的总波场。入射波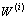 的表达式为:
的表达式为:
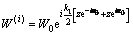 (19)
(19)
其中: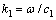 为入射波数;
为入射波数;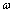 为圆频率;
为圆频率;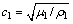 为入射波的相速度;
为入射波的相速度;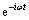 为时间谐和因子。
为时间谐和因子。
反射波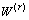 和折射波
和折射波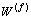 分别按(20)和(21)式定义:
分别按(20)和(21)式定义:
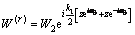 (20)
(20)
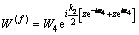 (21)
(21)
其中: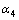 为折射角;
为折射角;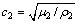 为介质Ⅱ的剪切波速;
为介质Ⅱ的剪切波速;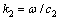 为介质Ⅱ的波数。
为介质Ⅱ的波数。
按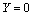 界面处的位移和应力的连续条件,得到折射角
界面处的位移和应力的连续条件,得到折射角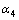 、反射波的位移幅值W2和折射波的位移幅值
、反射波的位移幅值W2和折射波的位移幅值
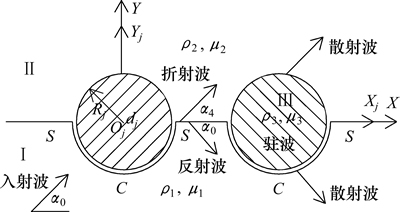
图5 稳态SH波的全空间模型
Fig. 5 Whole space model of steady state SH wave
W4的关系为
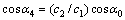
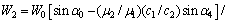
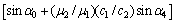
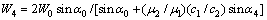 (22)
(22)
按上、下交界面S上剪应力的自由条件,得到介质Ⅱ内散射波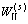 的表达式为
的表达式为
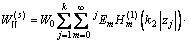
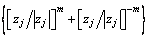 (23)
(23)
按波函数展开法,得到界面圆柱夹杂Oj内驻波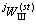 的表达式为
的表达式为
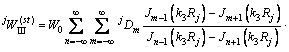
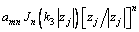 (24)
(24)
由公共边界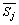 (或者
(或者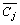 )上位移和应力的连续条件,得到:
)上位移和应力的连续条件,得到:
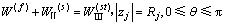 (25)
(25)
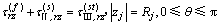 (26)
(26)
参考上半空间的Green函数,它们有相同的系数矩阵,得到:
 (27)
(27)
其中:
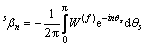
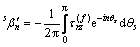 (28)
(28)
同理,得到介质Ⅰ内相应散射波 的表达式为
的表达式为
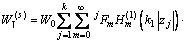
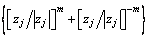 (29)
(29)
由入射波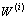 、反射波
、反射波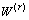 和介质Ⅰ内散射波
和介质Ⅰ内散射波 表达式可得
表达式可得
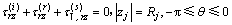 (30)
(30)
参考下半空间的Green函数,得到与求解下半空间Green函数相同的系数矩阵:
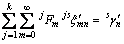 (31)
(31)
其中:
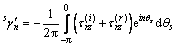 (32)
(32)
4 定解积分方程组
“契合”模型如图6所示,利用交界面S上位移和应力的连续条件,在交界面S上附加未知力系f1和f2,按求得的Green函数构造求解未知力系f1和f2的定解积分方程组:
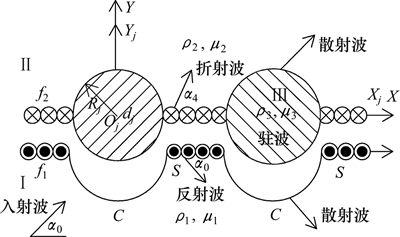
图6 “契合”模型
Fig. 6 Conjunction model
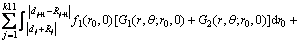

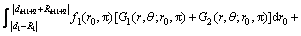

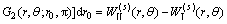 (33)
(33)
式中: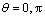 。
。
5 算例和结果分析
取界面圆柱夹杂Oj数k=2,给出了夹杂Oj边沿的动应力集中因子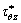 的分布状况。按坐标系
的分布状况。按坐标系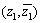 (或
(或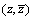 )下的应力场
)下的应力场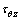 来计算。这里,假定两界面圆柱夹杂的半径相等,且为1.0,即
来计算。这里,假定两界面圆柱夹杂的半径相等,且为1.0,即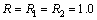 。
。
界面夹杂周围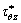 的分布如图7所示。由图7可知:在弹性SH波垂直入射,剪切模量比
的分布如图7所示。由图7可知:在弹性SH波垂直入射,剪切模量比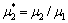 ,
,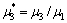 与波数比
与波数比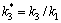 不变且入射波数
不变且入射波数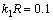 ,上半空间介质Ⅱ与下半空间介质Ⅰ的波数比
,上半空间介质Ⅱ与下半空间介质Ⅰ的波数比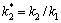 分别取0.5和4.0的条件下,当界面2个圆夹杂的距离参数
分别取0.5和4.0的条件下,当界面2个圆夹杂的距离参数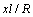 不变时,随着
不变时,随着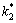 的增加,左端夹杂周围的动应力集中系数有所增加,同时,当
的增加,左端夹杂周围的动应力集中系数有所增加,同时,当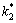 为恒量时,左端夹杂周围的动应力集中系数随着
为恒量时,左端夹杂周围的动应力集中系数随着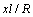 的增大而减小,说明右端夹杂对左端夹杂周围的动应
的增大而减小,说明右端夹杂对左端夹杂周围的动应
力集中系数有明显影响,由于右端夹杂的存在,左端夹杂周围的动应力集中系数增加,并且在区间315°≤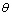 <360°时增加的幅度最明显,在区间180°≤
<360°时增加的幅度最明显,在区间180°≤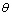 <225°时增加的幅度次之,但是,当
<225°时增加的幅度次之,但是,当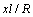 增大到3.0时,在区间315°≤
增大到3.0时,在区间315°≤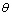 <360°与180°≤
<360°与180°≤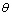 <225°左端夹杂周围的动应力集中系数的增加幅度,都比
<225°左端夹杂周围的动应力集中系数的增加幅度,都比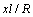 =0.5时小,并逐渐趋近于单个夹杂时的情况。
=0.5时小,并逐渐趋近于单个夹杂时的情况。
图8所示为当弹性SH波垂直入射且剪切模量比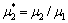 ,
,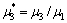 与波数比
与波数比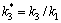 不变的情况下,入射波数k1R=0.5,k1R=1.0,上半空间介质Ⅱ与下半空间介质Ⅰ的波数比
不变的情况下,入射波数k1R=0.5,k1R=1.0,上半空间介质Ⅱ与下半空间介质Ⅰ的波数比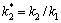 分别取0.5和4.0时,界面2个圆夹杂的距离参数
分别取0.5和4.0时,界面2个圆夹杂的距离参数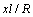 对界面夹杂周围
对界面夹杂周围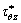 的影响。如图8可见:由于SH波入射波数k1R的影响,左端界面夹杂周围的动应力集中系数有明显增加,动应力集中系数的最大值点均发生在双相介质的界面上,即
的影响。如图8可见:由于SH波入射波数k1R的影响,左端界面夹杂周围的动应力集中系数有明显增加,动应力集中系数的最大值点均发生在双相介质的界面上,即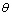 =0°,180°,但随着
=0°,180°,但随着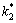 的增加,左端夹杂周围的动应力集中系数在
的增加,左端夹杂周围的动应力集中系数在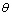 =180°时逐渐减小,但是在区间180°<
=180°时逐渐减小,但是在区间180°<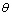 ≤225°与315°≤
≤225°与315°≤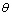 ≤360°呈增加趋势。
≤360°呈增加趋势。
图9所示为SH波以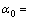 45°入射时,且入射波数
45°入射时,且入射波数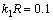 ,界面2个圆夹杂的距离参数分别取
,界面2个圆夹杂的距离参数分别取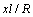 =0.5,1.0,3.0,剪切模量比
=0.5,1.0,3.0,剪切模量比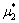 ,
,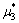 与波数比
与波数比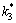 不变的情况下,上半空间介质Ⅱ与下半空间介质Ⅰ的波数比
不变的情况下,上半空间介质Ⅱ与下半空间介质Ⅰ的波数比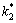 对左端界面夹杂动应力集中系数的影响。由图9可见:在
对左端界面夹杂动应力集中系数的影响。由图9可见:在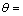 90°,270°时,左端界面夹杂动应力集中系数出现了突增的现象;随着上半空间介质Ⅱ与下半空间介质Ⅰ的波数比
90°,270°时,左端界面夹杂动应力集中系数出现了突增的现象;随着上半空间介质Ⅱ与下半空间介质Ⅰ的波数比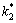 的增大,这种突增现象 从
的增大,这种突增现象 从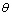 为90°和270°逐渐转变到
为90°和270°逐渐转变到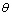 为135°和315°,
为135°和315°,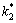 增大到一定程度的时候趋于稳定;在
增大到一定程度的时候趋于稳定;在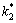 一定的条件下,随着
一定的条件下,随着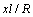 的增大,左端界面圆形夹杂周围的
的增大,左端界面圆形夹杂周围的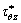 反而呈减小的趋势。
反而呈减小的趋势。
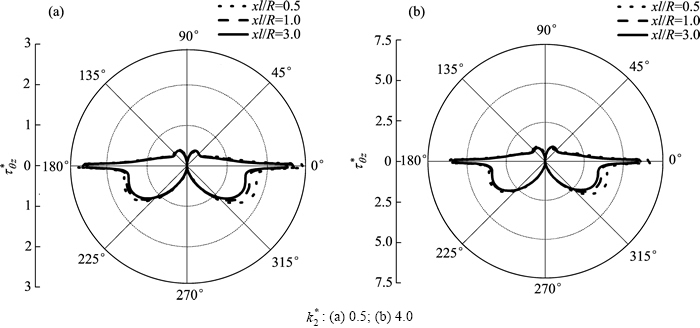
图7 界面夹杂周围 的分布(
的分布(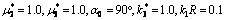 )
)
Fig. 7 Distribution of  around interfacial inclusion
around interfacial inclusion
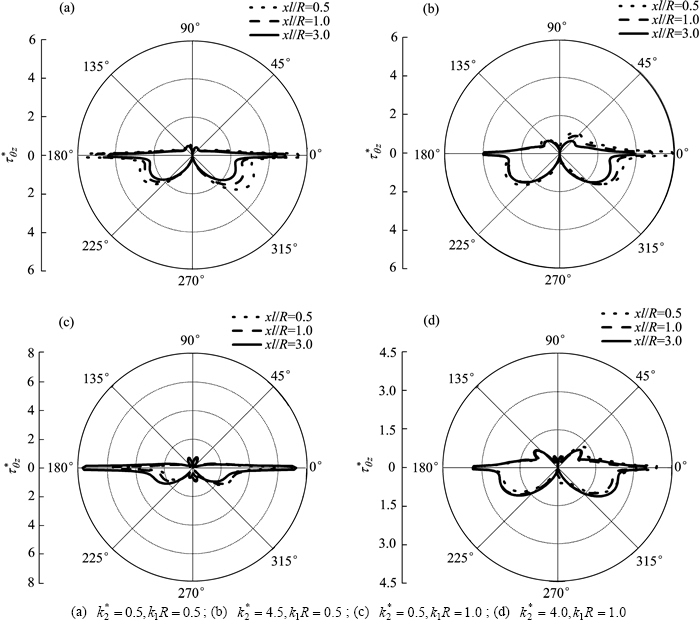
图8 界面夹杂周围 的分布(
的分布( )
)
Fig. 8 Distribution of  around interfacial inclusion
around interfacial inclusion
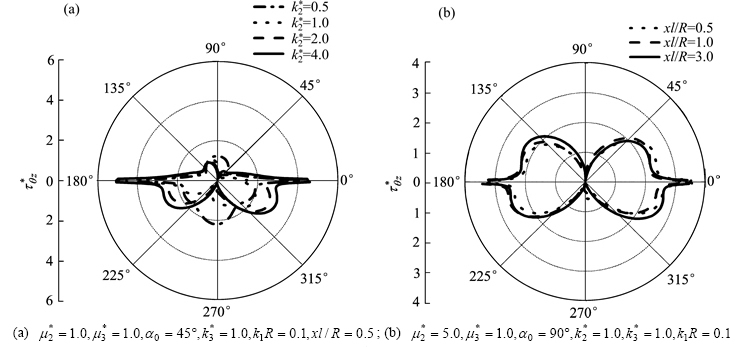
图9 界面夹杂周围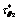 的分布
的分布
Fig. 9 Distribution of 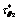 around interfacial inclusion
around interfacial inclusion
6 结论
1) 右端界面圆柱夹杂的存在使左端界面圆柱夹杂边沿的动应力集中因子有增大的趋势。
2) 动应力集中因子的最大值点均发生在脱胶界面上。
3) 右端夹杂对动应力集中系数的影响随着距离的增大而逐渐消失。
4) 随着介质波数比的增大,即当介质Ⅱ相对较“硬”时,动应力集中因子呈现递增的趋势,随着入射波数的增大,动应力集中因子呈现减小的趋势。这就表明,在工程实践中,尤其是在界面存在局部脱胶的情况下,需要格外注意多个界面夹杂之间的相互作用,这种作用可能造成较大的应力集中。
参考文献:
[1] PAOY H, MOW C C. Diffraction of elastic waves and dynamic stress concentrations[M]. New York: Crane and Russak, 1973: 15-50.
[2] LIU D K, GAI B Z, TAO G Y. Applications of the method of complex functions to dynamic stress concentrations[J]. Wave Motion, 1982(4): 293-304.
[3] TRIFUNAC M D. Scattering of plane SH waves by a semi-cylindrical canyon[J]. Earth Engineering and Structural Dynamics, 1973(1): 267-281.
[4] LEE V W, TRIFUNAC M D. Response of tunnels to incident SH-waves[J]. Journal of Engineering Mechanics, ASCE, 1979, 105: 643-659.
[5] 袁晓铭. 地表下圆形夹塞区出平面散射对地面运动的影响[J]. 地球物理学报, 1996, 39(3): 373-381.
YUAN Xianming. Effect of a circular underground inclusion on surface motion under incident plane SH waves[J]. Chinese Journal of Geophysics, 1996, 39(3): 373-381.
[6] 杨在林, 许华南, 黑宝平. 半空间椭圆夹杂与裂纹对SH波的散射[J]. 振动与冲击, 2013, 32(11): 56-61.
YANG Zailin, XU Huanan, HEI Baoping. Interaction of elliptical inclusion and crack under incident SH-wave in a half-space[J]. Journal of Vibration and Shock, 2013, 32(11): 56-61.
[7] 杨在林, 许华南, 黑宝平. SH波上方垂直入射时界面附近椭圆夹杂与裂纹的动态响应[J]. 岩土力学, 2013, 34(8): 2378-2384.
YANG Zailin, XU Huanan, HEI Baoping. Dynamic response of elliptical inclusion and crack near interface under vertically incident SH-wave from above[J]. Rock and Soil Mechanics, 2013, 34(8): 2378-2384.
[8] 刘殿魁, 刘宏伟. SH波散射与界面圆孔附近的动应力集中[J]. 力学学报, 1998, 30(5): 597-604.
LIU Diankui, LIU Hongwei. Scattering and dynamic stress concentration of SH wave by interface circular hole[J]. Acta Mechanica Sinica, 1998, 30(5): 597-604.
[9] 汪越胜, 王铎, 马兴瑞, 等. 奇异积分方程在裂纹体弹性波散射问题中的应用[J]. 力学进展, 1997, 27(1): 39-55.
WANG Yuesheng, WANG Duo, MA Xingrui, et al. On the application of singular integral equation to the scattering problems of elastic waves by cracks[J]. Advances in Mechanics, 1997, 27(1): 39-55.
[10] 齐辉, 杨杰. SH波入射双相介质半空间浅埋任意位置圆形夹杂的动力分析[J]. 工程力学, 2012, 29(7): 320-327.
QI Hui, YANG Jie. Dynamic analysis for shallowly buried circular inclusions of arbitrary positions impacted by SH-wave in bi-material half space[J]. Engineering Mechanics, 2012, 29(7): 320-327.
[11] QI H, YANG J, SHI Y, TIAN J Y. Dynamic analysis for circular inclusion near interfacial crack impacted by SH wave in half space[J]. Journal of Mechanics, 2012, 28(1): 143-151.
[12] QI H, YANG J. Dynamic analysis for circular inclusions of arbitrary positions near interfacial crack impacted by SH-wave in half-space[J]. European Journal of Mechanics-A/Solids, 2012, 36: 18-24.
[13] 齐辉, 赵春香, 黄敏. 出平面线源荷载作用下半空间内浅埋圆孔对半圆形凸起的圆柱形弹性夹杂的动力影响[J]. 振动与冲击, 2013, 32(17): 109-112.
QI Hui, ZHAO Chunxiang, HUANG Min. Dynamic effect of a subsurface cavity in half space under out-of-plane line source load on a cylindrical elastic inclusion with a semi-cylindrical hill[J]. Journal of Vibration and Shock, 2013, 32(17): 109-112.
[14] 齐辉, 蔡立明, 潘向南, 等. 直角域中凸起和孔洞对SH波的散射与地震动[J]. 岩土力学, 2015, 36(2): 347-353.
QI Hui, CAI Liming, PAN Xiangnan, et al. Scattering and seismic ground motion of circular cavity and semi-circular hill with SH wave in a quarter space[J]. Rock and Soil Mechanics, 2015, 36(2): 347-353.
[15] 齐辉, 蔡立明, 潘向南, 等. 含半圆形凸起的直角域对平面SH波的地震动[J]. 岩土工程学报, 2015, 37(7): 1294-1299.
QI Hui, CAI Liming, PAN Xiangnan, et al. Seismic ground motion of an elastic quarter space subjected by plane SH wave with a semi-circular cylindrical hill[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(7): 1294-1299.
[16] 齐辉, 蔡立明, 罗广龙, 等. 双相介质半空间中圆孔对透射SH波的稳态分析[J]. 爆炸与冲击, 2015, 35(4): 591-598.
QI Hui, CAI Liming, LUO Guanglong, et al. Steady state analysis for circular cavity impacted by transmitted SH wave in a bi-material half space[J]. Explosion and Shock Waves, 2015, 35(4): 591-598.
[17] 高春, 齐辉, 潘向南, 等. 界面点源和半圆柱在直角域中的反平面散射[J]. 哈尔滨工业大学学报, 2015, 47(10): 94-99.
GAO Chun, QI Hui, PAN Xiangnan, et al. Anti-plane scattering of interfacial point source load and semi-circular cylinder in an elastic quarter space[J]. Journal of Harbin Institute of Technology, 2015, 47(10): 94-99.
(编辑 赵俊)
收稿日期:2015-03-26;修回日期:2015-06-09
基金项目(Foundation item):国家自然科学基金资助项目(51379048) (Project(51379048) supported by the National Natural Science Foundation of China)
通信作者:齐辉,博士,教授,从事弹性波动理论及应用研究;E-mail:qihui205@sina.com