DOI: 10.11817/j.issn.1672-7207.2017.11.032
基于离散元分析盾构动态掘进引起的无黏性地层主应力特征
瞿同明1,王树英1, 2,傅金阳1,阳军生1
(1. 中南大学 土木工程学院,湖南 长沙,410075;
2. 重载铁路工程结构教育部重点实验室,湖南 长沙,410075)
摘要:为阐明土压平衡盾构掘进引起无黏性地层主应力响应特征,采用离散元方法建立土压平衡盾构动态掘进二维数值模型。在同一盾构掘进速率下,考虑不同土仓排土速率,分析盾构掘进引起的地表沉隆变化;取上、下2组极限排土工况,研究盾构掘进过程中排土速率引起的砂土地层主应力变化特征。研究结果表明:盾构掘进引起的地层主应力大小和方向的变化与土仓排土速率密切相关;在不排土工况下, 地层主应力的量值和偏转明显,掘进引起地层主应力响应的范围要比排土工况的大,且主应力比排土工况的更不容易达到稳定状态。在排土工况下,掌子面前方会形成明显的应力释放区;在同一排土速度下,掘进过程中地层大、小主应力随盾构掘进变化趋势相似,但变化的程度不同。
关键词:土压平衡盾构;离散元;排土速度;主应力
中图分类号:U455.4 文献标志码:A 文章编号:1672-7207(2017)11-3083-09
Study on characteristics of principal stresses induced by dynamic EPB shield tunneling in non-cohesive stratum based on DEM
QU Tongming1, WANG Shuying1, 2, FU Jinyang1, YANG Junsheng1
(1. School of Civil Engineering, Central South University, Changsha 410075, China;
2. Key Laboratory of Engineering Structure of Heavy Railway, Ministry of Education, Changsha 410075, China)
Abstract: Two dimensional numerical simulations based on the discrete element method (DEM) were carried out to analyze the response characteristics of principal stress in non-cohesive stratum during the tunneling of the earth pressure balance (EPB) shield. Groups of shield tunneling cases with various soil-discharging speeds in the chamber and an identical advancing velocity were numerically conducted to investigate the changes of vertical displacement at ground surface. Two limit cases among those discharge speeds were determined to demonstrate the variations of principal stresses caused by tunneling. The results show that magnitudes and rotation angles of principal stress in stratum constantly vary and are closely related with soil-discharging speeds in chamber. In the case without discharging soil, magnitudes and directions of principal stress dramatically change and this affected area of stress is larger than that in the soil-discharging case, with a greater difficulty of keeping stress stable during tunneling. In the soil-discharging case, a remarkable stress release area forms in front of tunnel face. Furthermore, the variation tendencies of both major and minor principal stresses are similar in the case of identical discharge speeds, but the values of variation remain different from each other.
Key words: earth pressure balance shield; discrete element method; soil-discharging speed; principal stress
主应力轴旋转是一个在工程建设中普遍存在又常被忽略的问题。主应力轴旋转是指主应力方向相对于土的沉积方向(或某固定方向)发生旋转,产生与方向固定条件下不同的力学特性,例如造成土体的黏聚力和内摩擦角显著变化,土体强度下降等。盾构开挖前,盾构隧道所处地层初始最大主应力方向通常为竖直方向,初始最小主应力方向为水平方向。在盾构掘进过程中,土体所受大主应力方向沿水平方向旋转。由于一般沉积土层的各向异性明显,竖直向强度大于水平向强度,主应力方向的旋转造成土体强度降低,容易导致土体出现更加明显的塑性变形,在不排水情况下,甚至会使砂土液化破坏[1],因此,有必要加强对隧道开挖过程中土体主应力变化的研究。在模型试验和现场实践中,受制于监测仪器的布置难度和布设数量,很难全面记录盾构掘进引起的地层应力变化过程,也无法监测主应力相关的参数变化,因而,以往关于隧道开挖过程中引起土体的应力状态变化的研究多通过数值模拟来完成[2-6]。EBERHARDT[2]使用有限元方法对隧道掌子面前方主应力变化引起的岩石断裂及裂缝扩展问题进行了研究;WANG[3]采用有限单元方法对硬岩地层条件下隧道开挖过程主应力轴旋转变化引起周边围岩的稳定性和位移变化进行分析;ZHANG等[4]依托锦屏2号引水隧洞,研究了隧道开挖时主应力旋转引起的岩石分层断裂现象;肖军华等[5]结合有限元模拟与现场实测方法,研究了主应力轴旋转对地铁荷载作用下隧道下卧软黏土累积变形的影响;熊良宵[6]通过FLAC3D数值仿真技术研究了深埋隧道采用矿山法开挖引起的应力变化过程。常规的有限元方法基于连续的弹塑性体假定,无法对动态大变形问题进行数值仿真,而土压平衡盾构隧道掘进过程伴随着土仓排土等动态大变形现象,将其粗放地当作连续介质问题,必然存在着许多不足。离散单元法克服了有限单元法的连续性假定问题,对具有明显离散特性的砂卵石等地层和动态大变形问题的研究具有较大优势。目前离散元方法虽然也被越来越多地引入到盾构隧道的研究中[7-16],但较少考虑盾构掘进过程中的土仓排土过程。事实上,对于土压平衡盾构而言,土仓的排土速率作为重要的掘进参数,直接影响到掌子面的稳定和前方地层的扰动程度。瞿同明等[17]考虑盾构动态排土,基于PFC2D分析了掘进引起的地层位移响应规律和掌子面应力的分布与变化趋势,但并未考虑模型的缩尺效应。模型地层应力与实际地层应力差别较大,且盾构排土方式偏于粗放,难于控制。本文作者基于改进的盾构隧道离散元数值仿真掘进模型,分析土压平衡盾构在同一掘进速度、不同土仓排土速度下掘进引起的地表隆沉响应。基于2组极限排土工况,研究掘进引起的砂土地层主应力量值、主应力轴旋转角度的变化规律。
1 离散元模型
1.1 颗粒材料属性
PFC通过一定数目的颗粒或颗粒簇来模拟土体颗粒,颗粒间的细观参数与土体宏观参数并不存在一一对应的关系。为明确离散元所用细观参数对应的宏观力学特性,建立双轴数值试验:令σ1为大主应力,σ3为小主应力,分别在围压(σ3)为50,100,200和500 kPa的条件下进行加载,得出模拟土体的应力-应变关系。
双轴数值试验的建立过程为:1) 建立上、下、左、右4面墙体,生成宽×高为150 mm×300 mm的试样空间;2) 按级配曲线(见图1)生成试样颗粒,中值粒径d50为7.6 mm,不均匀系数Cu为1.21,孔隙率为0.191;3) 施加围压;4) 加载顶板,直至试样轴向应变达到20%。双轴数值模型如图2所示,颗粒本构选择线性接触模型,所用细观参数如表1所示。在不同围压条件下的主应力差(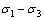 )与轴向应变(
)与轴向应变( )曲线如图3所示。
)曲线如图3所示。
当所有试样轴向应变达到15%后,主应力差趋于稳定,此时可认为试样达到临界破坏状态。取轴向应变为15%时的主应力差作为破坏点,将每个围压下的强度值绘制成莫尔强度包络曲线,得出模拟土体颗粒的黏聚力为0 kPa,内摩擦角为17.8°。
1.2 盾构掘进离散元模型
基于离散元商业软件PFC2D,首先生成左、右、下3面墙体边界,上侧为自由边界;初始地层采用“落雨法”生成,即首先在墙体内生成颗粒,颗粒在重力作用下堆积形成静止土压力系数为0.75的初始地层。由于土体颗粒数目和计算机能力的限制,将实际模型缩小40倍,模型生成土层长×宽为1.2 m×0.8 m,颗粒数目22 558个,颗粒和墙体的细观参数与双轴数值模型一致,孔隙率为0.189(与双轴试样仅存在0.002的差异)。依据相似原理[18],当尺寸缩小N倍而重力加速度放大N倍时,模型地层与原型具有相同的有效应力。GARNIER等[19]的研究表明,为减少由于模型缩尺带来的尺寸效应问题,可将重力加速度放大40倍;通过这种方法,仿真模型将保持和实际工况同样的应力,但模型发生的位移和变形需要相应放大40倍。离心机缩尺模型与实际模拟模型的换算如表2[18]所示。

图1 级配曲线
Fig. 1 Grading curve

图2 双轴试样
Fig. 2 Biaxial test sample
表1 离散元材料参数
Table 1 Material parameters of DEM sample


图3 主应力差与轴向应变曲线
Fig. 3 Major principal deviator stress versus major axial strain
表2 主要物理量比尺关系
Table 2 Scales of main parameters

采用PFC墙体来模拟盾壳,盾构直径为0.2 m,埋深为0.4 m。因研究重点在盾构前方和上方,盾构下方保留1.5倍洞径,前方保留5倍洞径,盾构土仓长×高为0.06 m×0.2 m。在40g重力加速度下,根据相似准则[18-19],模拟实际原型盾构(直径为8 m,埋深为16 m)。由于是二维模型,不能有效考虑刀盘开口率布置情况,这里忽略刀盘开口率的影响,刀盘完全敞开。盾构的掘进通过赋予墙体一定的速度来实现,在排土区域一定的情况下,盾构掘进速度选定为0.01 m/s。遍历土仓下部靠近隔板的螺旋输送机位置处颗粒,设置向土仓内运动的速度以模拟螺旋输送机的排土过程,排土区域与盾构相对位置保持不变,排土区域长×高为0.03 m×0.03 m,通过控制颗粒移动速率来模拟不同的螺旋输送机排土速度。当颗粒到达盾构隔板之后,为减少浮点颗粒对计算速度的影响,删除排出土仓的颗粒。盾构模型如图4所示。为明确描述盾构的实际掘进情况,下面所有的物理量都将数值模型还原为实际模型尺度来进行分析。
为确定数值盾构模型在不同排土速度下地表位移的响应规律,在盾构掘进速度为0.4 m/s的条件下,对先前设定的排土区域分别选择排土速度为0,0.04,0.40,2.00,3.20和4.00 m/s,使盾构连续推进1.2 m。需要说明的是,为获得准静态环境,模型的时步必须控制在1个较小值,这导致每模拟现实的1 s就需要12 h左右(处理器为Intel Core i5,CPU内存为2.8 GHz,RAM内存为4 GB)。鉴于离散元巨大的计算量,本模拟选定的盾构掘进速度相对于实际情况要大得多。为获得隆起和沉降的地表响应,相应地,盾构排土速度也比现实工况的大。

图4 盾构数值模型
Fig. 4 EPB shield model
1.3 离散元中的主应力计算原理
应力属于连续介质范畴,在离散介质中只存在颗粒间的接触力和颗粒位移,空隙区域不存在力。由于应力概念对于描述材料行为具有重要意义,因此,通过平均化的方法,在离散元中引入应力概念。具体引入方法[20]为
 (1)
(1)
其中: 为作用在一定区域内的应力张量,Pa,
为作用在一定区域内的应力张量,Pa, 为颗粒中的平均应力张量,Pa;
为颗粒中的平均应力张量,Pa; 为区域内的颗粒数;
为区域内的颗粒数; 为颗粒体积,m3。颗粒的平均应力通过接触力来确定:
为颗粒体积,m3。颗粒的平均应力通过接触力来确定:
 (2)
(2)
其中: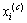 为颗粒与颗粒间的接触位置,m;
为颗粒与颗粒间的接触位置,m; 为颗粒中心位置,m;
为颗粒中心位置,m; 是从颗粒中心指向接触位置的单位法向量;
是从颗粒中心指向接触位置的单位法向量; 是接触力,N;
是接触力,N; 为颗粒间接触的数量。通过颗粒应力平均化与区域应力平均化方法,可以在离散元中得到作用在一定区域的水平应力
为颗粒间接触的数量。通过颗粒应力平均化与区域应力平均化方法,可以在离散元中得到作用在一定区域的水平应力 和竖直应力
和竖直应力 。
。
根据材料力学原理,最大主应力 和最小主应力
和最小主应力 的计算公式为
的计算公式为
 (3)
(3)
式中: 为切应力。
为切应力。
大主应力方向与竖直方向的夹角计算公式为
 (4)
(4)
盾构在掘进前初始地层大主应力方向为竖直方向,小主应力方向为水平方向,盾构掘进引起的主应力轴偏转角度可用掘进过程中大主应力方向与竖直方向的夹角 减去其初始夹角来计量。偏转角度为正,表示主应力轴往逆时针方向旋转;偏转角度为负,表示主应力轴往顺时针方向旋转。
减去其初始夹角来计量。偏转角度为正,表示主应力轴往逆时针方向旋转;偏转角度为负,表示主应力轴往顺时针方向旋转。
2 不同排土速度下盾构掘进引起地表隆沉响应
在一般情况下,土压平衡盾构掘进过程中,当土仓进土量少于排土量时,土仓内土压力降低,掌子面附近土体向土仓内移动导致地表沉降;当土仓进土量超过排土量时,土仓内土压力增加,掌子面附近土体被挤压引起地表隆起。提取盾构在6种排土速度下掘进1.2 m时地表的竖向位移,绘出不同排土速度下地表竖向位移响应曲线,如图5所示。由图5可知:当不排土和排土速度为0.04 m/s时,掌子面前方土体会发生隆起,排速越小则隆起量越大;当排土速度分别为0.40,2.00,3.20和4.00 m/s时,掌子面前方地表会发生沉降,排速越大则地表沉降越大。为展现盾构不同排速掘进引起的地表位移特征,当盾构掘进停止时,以掌子面前方1.5倍洞径位置(水平坐标x=21.2 m)地表的颗粒为例,将此颗粒在不同排土速度下的竖向位移拟合成曲线,如图6所示。根据拟合结果,当盾构排土速度为0.26 m/s时,此处地表的沉降为0 m,说明此时掌子面土压力基本保持平衡。当排土速度远离平衡排速(0.26 m/s)时,地表竖向位移相应的发生隆起或沉降,排速增大则地表沉降;排速减小则地表隆起。在同一掘进速度、不同排速下地表的竖向位移变化曲线表明:土压平衡盾构数值模型具备反映盾构掘进引起地层响应的能力;当排土速度为4 m/s时,地表沉降值趋于极限;当土仓不排土时,地表隆起值趋于极限。为表征盾构掘进中土仓排土引起的力学响应特征,在2种极限排速下对盾构引起的主应力变化进行分析。

图5 不同排速下地表竖向位移响应曲线
Fig. 5 Vertical displacement of ground surface due to tunneling with various discharging speeds

图6 特征点竖向位移与排土速度相对关系
Fig. 6 Relation between vertical displacement and soil-discharging speeds at characteristic position
3 不同排土速度下盾构掘进引起地层主应力变化特征
3.1 盾构掘进引起的主应力偏转现象
盾构掘进前的应力场如图7(a)所示。盾构掘进前,模型中除边界处颗粒存在边界效应外,初始地层的大主应力方向为竖直方向,小主应力为水平方向。盾构在不排土工况下掘进1.2 m时地层应力场如图7(b)所示。在掌子面前方,大、小主应力均比初始地层增大许多,增大值随距离掌子面越远而逐渐减小。在其他位置,主应力的方向会发生偏转,但在量值上的变化并不明显。在排土速度为4 m/s的条件下,盾构掘进1.2 m时地层应力场如图7(c)所示。在掌子面前方会发生明显的应力释放,主应力明显减小,在距离掌子面较远处,主应力与初始地层相似,主应力方向会发生轻微偏转。从图7(b)和7(c)可以看出:在掌子面前方,主应力轴的大小变化明显;在掌子面前上方,主应力轴往逆时针方向偏转;在掌子面前下方,主应力轴往顺时针方向偏转。

图7 地层应力场
Fig. 7 Stress fields of stratum
3.2 盾构掘进引起的主应力分析
为进一步研究盾构掘进引起地层主应力的变化情况,在盾构掌子面前方土体潜在破坏区附近[21]选取4个监测区域(见图4),监测中心与盾构掌子面中心的相对位置分别为(D/4, 3D/2),(5D/4, 3D/2),(D/4, 0), (5D/4, 0) (D为盾构直径),并依次编号为第1~4监测区。监测区在盾构掘进过程中与盾构的相对位置保持不变,分别对主应力的量值变化和偏转角度变化进行分析。
3.2.1 随盾构掘进主应力量值变化
由于地层应力与埋深和土体质量有关,为更明确地描述不同位置地层主应力随盾构掘进的变化趋势,将盾构掘进过程中土体的大、小主应力 和
和 除以相应位置初始地层大主应力
除以相应位置初始地层大主应力 ,以克服不同埋深和土体质量的影响。在土仓不排土和土仓排土速度为4 m/s的工况下,分别记录地层主应力大小随盾构掘进变化关系,如图8~9所示。
,以克服不同埋深和土体质量的影响。在土仓不排土和土仓排土速度为4 m/s的工况下,分别记录地层主应力大小随盾构掘进变化关系,如图8~9所示。
从图8可以看出:在盾构掌子面上方的第1监测区域内,掘进过程中不论是否排土,大主应力均比初始地层主应力稍大,二者比值在1.1~1.3之间波动;在第2监测区域内,在排土与不排土工况下,大主应力比变化很小,比值在1.0附近,这说明在这个区域内,盾构掘进引起的地层主应力变化不大。第3监测区域为盾构掌子面前方,这是盾构掘进引起地层响应最剧烈的区域。在排土工况下,区域内土体应力得到释放,主应力变小,大主应力比随盾构掘进逐渐稳定,并降低至0.4左右;在不排土工况下,大主应比随盾构掘进逐渐上升,并最终稳定在2.3左右,应力比值变化明显。在第4监测区域内,在排土工况下,大主应力会稍大于初始地层应力,应力比平均值约为1.1,盾构的掘进对地层影响已经不大;在不排土工况下,大主应力比随盾构掘进明显增大,最终稳定在2.0左右,与第3监测区相比,应力比有所下降,但依然变化较大。

图8 大主应力比随盾构掘进变化曲线
Fig. 8 Variation curves of major principal stress ratio during tunneling

图9 小主应力比随盾构掘进变化曲线
Fig. 9 Variation curves of minor principal stress ratio during tunneling
盾构掘进前地层小主应力与初始地层大主应力的比值可看作是初始地层静止土压力系数。由图9可知:在4个监测区域内,静止土压力系数基本相同,都为0.75左右。在第1和第2监测区内,小主应力比 ( )随盾构掘进变化不大:在排土工况下,2个区域内的小主应力比值基本小于初始地层的静止土压力系数值,约为0.70;在不排土工况下,2个区域的小主应力比值稍大于初始地层的静止土压力系数值,约为0.80。第3监测区是盾构掘进土体应力响应最明显的区域:在不排土工况下,小主应力比随盾构掘进上升明显,并逐渐稳定在1.5左右;在排土工况下,小主应力比随盾构掘进下降明显,并很快稳定在0.25左右。第4监测区内小主应力比也呈现较大的变化:在不排土工况下,小主应力比上升明显,最后逐渐稳定在1.25左右,但上升的幅度比第3监测区的小,这说明距离盾构越远则盾构掘进对掌子面前方土体的影响越小;排土工况下,小主应力比随盾构掘进略微减小,很快稳定在0.62左右。
)随盾构掘进变化不大:在排土工况下,2个区域内的小主应力比值基本小于初始地层的静止土压力系数值,约为0.70;在不排土工况下,2个区域的小主应力比值稍大于初始地层的静止土压力系数值,约为0.80。第3监测区是盾构掘进土体应力响应最明显的区域:在不排土工况下,小主应力比随盾构掘进上升明显,并逐渐稳定在1.5左右;在排土工况下,小主应力比随盾构掘进下降明显,并很快稳定在0.25左右。第4监测区内小主应力比也呈现较大的变化:在不排土工况下,小主应力比上升明显,最后逐渐稳定在1.25左右,但上升的幅度比第3监测区的小,这说明距离盾构越远则盾构掘进对掌子面前方土体的影响越小;排土工况下,小主应力比随盾构掘进略微减小,很快稳定在0.62左右。
由图8~9可知:地层主应力在排土工况下比在不排土工况下更快趋于稳定,同时,在同一监测区域内,不排土工况下盾构掘进引起地层主应力的响应值要比排土工况的大。这说明对于土压平衡盾构而言,排土速度对于掘进引起的力学响应差别很大。在连续介质力学中,摩尔-库伦强度理论认为土体的破坏是在大、小主应力共同作用下的结果。令 ,
, (其中,F为土体的安全系数,λ为小主应力与大主应力的比值)。对于黏聚力为0的砂性土体,当主应力满足F>1时,土体处于弹塑性状态;当大、小主应力关系满足F=1时,可认为土体达到极限强度,发生剪切破坏。图10所示为掌子面前方(第3监测区)F与λ变化曲线。由图10可知:在只考虑主应力量值变化的情况下,掌子面前方土体F趋近于1,即土体有破坏的趋势。在排土工况下,盾构掘进引起安全系数F与主应力比值λ波动较剧烈;随着掘进距离增加,F与λ波动幅度变小。这表明盾构在排土工况下,特别是在盾构始发或者停机后掘进时,掌子面前方土体伴随着盾构挤压加载和土仓排土卸载,应力状态非常复杂。不排土工况下,F与λ先增加然后逐渐降低,并趋于稳定。这是因为盾构掘进时挤压前方土体,主要增加土体的水平向应力。图11所示为莫尔圆变化情况。由图11可知:在土体的库仑强度线和竖向应力
(其中,F为土体的安全系数,λ为小主应力与大主应力的比值)。对于黏聚力为0的砂性土体,当主应力满足F>1时,土体处于弹塑性状态;当大、小主应力关系满足F=1时,可认为土体达到极限强度,发生剪切破坏。图10所示为掌子面前方(第3监测区)F与λ变化曲线。由图10可知:在只考虑主应力量值变化的情况下,掌子面前方土体F趋近于1,即土体有破坏的趋势。在排土工况下,盾构掘进引起安全系数F与主应力比值λ波动较剧烈;随着掘进距离增加,F与λ波动幅度变小。这表明盾构在排土工况下,特别是在盾构始发或者停机后掘进时,掌子面前方土体伴随着盾构挤压加载和土仓排土卸载,应力状态非常复杂。不排土工况下,F与λ先增加然后逐渐降低,并趋于稳定。这是因为盾构掘进时挤压前方土体,主要增加土体的水平向应力。图11所示为莫尔圆变化情况。由图11可知:在土体的库仑强度线和竖向应力 不变的情况下,水平应力
不变的情况下,水平应力 从
从 到
到 逐渐变大,莫尔圆变小且远离库伦强度线,因此安全系数变大;当
逐渐变大,莫尔圆变小且远离库伦强度线,因此安全系数变大;当 在数值上超过
在数值上超过 并继续增加到
并继续增加到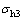 和
和 时,
时, 从小主应力转变为大主应力,莫尔圆变大且逐渐接近库伦强度线,因而安全系数变小。这解释了不排土工况下土体F在盾构掘进中开始增加,而后稳定降低的现象(见图10)。
从小主应力转变为大主应力,莫尔圆变大且逐渐接近库伦强度线,因而安全系数变小。这解释了不排土工况下土体F在盾构掘进中开始增加,而后稳定降低的现象(见图10)。

图10 掌子面前方(第3监测区)F与λ变化曲线
Fig. 10 Changing curves of F and λ at front of tunnel face (in the third monitoring area)
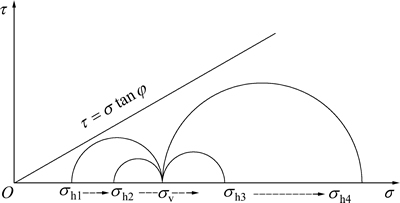
图11 莫尔圆变化情况
Fig. 11 Changing condition of mohr’s circle
3.2.2 随盾构掘进主应力轴偏转角度变化
选取4个测量区域(见图4)对盾构掘进引起土体主应力轴偏转角度发生变化的情况进行分析。由于式(4)中得到的角度范围仅限于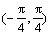 ,为对主应力轴偏转角度超过45°的情况进行说明,结合莫尔圆原理将主应力偏转的角度范围扩充为(-90°, 90°)。以初始地层主应力轴的位置作为初始位置,统计各个区域内主应力轴偏转的角度随盾构掘进的变化情况,如图12所示。
,为对主应力轴偏转角度超过45°的情况进行说明,结合莫尔圆原理将主应力偏转的角度范围扩充为(-90°, 90°)。以初始地层主应力轴的位置作为初始位置,统计各个区域内主应力轴偏转的角度随盾构掘进的变化情况,如图12所示。

图12 主应力轴偏转角度随盾构掘进变化曲线
Fig. 12 Changes in deflection angles of principal stress axis during the tunneling
由图12可知:在第1测量区,2种工况下的主应力偏转角度均为负值,即主应力轴均往顺时针方向旋转;当不排土时,应力轴的旋转角度总体要比排土时的稍大,但角度变化幅度要比排土工况时的小,旋转角度随盾构掘进基本稳定在15°左右。在第2测量区,土仓排土对主应力轴偏转角度的方向影响较大;在排土工况下,土体主应力轴往逆时针方向旋转,偏转角度随盾构掘进逐渐稳定在45°左右;在不排土工况下,主应力轴沿顺时针方向旋转,随盾构掘进,偏转角度波动幅度较大,但基本小于25°。在第3测量区,主应力轴偏转角度变化最剧烈:不排土工况下,随盾构掘进主应力轴偏转角度增加明显,并最终稳定在65°左右;在排工工况下,主应力轴偏转角度波动很大,时而往逆时针方向偏转,时而往顺时针方向偏转,这主要是土仓排土引起掌子面地层应力释放,土体颗粒受力复杂所致。在第4测量区内,2种工况下的主应力轴均向逆时针方向偏转,偏转角度随盾构掘进均稳定在30°左右。
图12表明盾构掘进引起的地层主应力偏转方向与排土速度、距掌子面相对位置有关。在第2和第3监测区内,排土速度对地层主应力轴偏转方向影响很大,而在第1和第4监测区内,2种极限排速下的主应力轴偏转方向一致,角度接近;说明在第2和第3监测区连线方向(掌子面的斜上方)是盾构排速对地层主应力轴偏转的主要影响区域。当盾构不排土时,掌子面前方土体的主应力轴偏转现象最严重,偏转角度稳定在75°左右;这是盾构土仓内压力过大,土仓内土体挤压前方土体所致。当排土速度很大时,掌子面上方土体主应力轴偏转角度最大,在45°左右,这是掌子面土体颗粒流入土仓,掌子面上方颗粒向下滑动所致。根据摩尔-库仑理论,土体在发生剪切破坏时,剪切方向与大主应力方向的夹角为(45°+φ/2)。土体主应力轴旋转,会引起剪切破坏的方向发生变化。因此,盾构在掘进过程中,掌子面前方土体破坏的模式和形态在不同排土速率下会表现出很大差异。
4 结论
1) 盾构掘进引起初始地层主应力变化,主要表现为主应力的变化和主应力轴方向的偏转。在盾构掘进过程中,螺旋输送机的排土速度对地层应力影响较大。当盾构不排土时,盾构对土体的挤压力从掌子面向前方地层远处扩散,对掌子面前方主应力扰动明显。在排土速度较大时,掌子面附近土体形成一个应力释放区,对原始地层应力扰动范围远比不排土时的小。土仓的排土对保持前方土体应力的稳定有着重要的影响。
2) 在不排土工况下,盾构掘进引起的地层主应力响应值要比排土工况下的大,且主应力比排土工况下的更不容易达到稳定。在同一排土速度下,在掘进过程中,地层大、小主应力的变化趋势相似,但量值变化的程度不同;当应力满足 时,土体将发生剪切破坏。在排土工况下,伴随着盾构挤压加载和土仓排土卸载,掌子面前方区域土体的应力状态复杂,土体安全系数变化幅度大,但变化平均值比不排土工况下的高。
时,土体将发生剪切破坏。在排土工况下,伴随着盾构挤压加载和土仓排土卸载,掌子面前方区域土体的应力状态复杂,土体安全系数变化幅度大,但变化平均值比不排土工况下的高。
3) 盾构掘进引起的地层主应力偏转方向与排土速度、距掌子面相对位置有关。当盾构不排土时,掌子面前方土体主应力轴发生逆时针大角度偏转,偏转角度可达75°;当排土速度较大时,掌子面前方土体主应力轴顺时针旋转。不论盾构是否排土,在盾构前上方地层,主应力轴逆时针旋转;在盾构前下方地层,主应力顺时针旋转。主应力的偏转将引起盾构掌子面破坏模式和破坏形态的变化。
参考文献:
[1] 刘元雪, 郑颖人. 考虑主应力轴旋转对土体应力-应变关系影响的一种新方法[J]. 岩土工程学报, 1998, 20(2): 45-47.
LIU Yuanxue, ZHENG Yingren. A new method to analyze the influence of principal stress axes rotation on the stress-strain relation of soils[J]. Chinese Journal of Geotechnical Engineering, 1998, 20(2): 45-47.
[2] EBERHARDT E. Numerical modelling of three-dimension stress rotation ahead of an advancing tunnel face[J]. International Journal of Rock Mechanics & Mining Sciences, 2001, 38: 499-518.
[3] WANG Junqi. Numerical study on the relationship of the axis orientation of deeply buried circular tunnel and the direction of horizontal in-situ stress[J]. Applied Mechanics and Materials, 2012, 117/118/119(3): 1723-1727.
[4] ZHANG C, ZHOU H, FENG X, et al. Layered fractures induced by principal stress axes rotation in hard rock during tunnelling[J]. Materials Research Innovations, 2011, 15(S1): 527-530
[5] 肖军华, 许世芹, 韦凯, 等. 主应力轴旋转对地铁荷载作用下软黏土累积变形的影响[J]. 岩土力学, 2013, 34(10): 2938-2944.
XIAO Junhua, XU Shiqin, WEI Kai, et al. Influences of rotation of principal stress axis on accumulative deformation of soft clay under subway cyclic loading[J]. Chinese Journal of Rock and Soil Mechanics, 2013, 34(10): 2938-2944.
[6] 熊良宵, 杨林德. 深埋隧洞开挖造成的应力变化过程[J]. 中南大学学报(自然科学版), 2009, 40(01): 236-242.
XIONG Liangxiao, YANG Linde. Stress evolution of deep cavern induced by excavating[J]. Journal of Central South University (Science and Technology), 2009, 40(1): 236-242
[7] MAYNAR M, RODRIGUEZ M. Discrete numerical model for analysis of earth pressure balance tunnel excavation[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2005, 131(10): 1234-1242.
[8] 朱伟, 钟小春, 加瑞. 盾构隧道垂直土压力松动效应的颗粒流模拟[J]. 岩土工程学报, 2008, 30(5): 750-754.
ZHU Wei, ZHONG Xiaochun, JIA Rui. Simulation on relaxation effect of vertical earth pressure for shield tunnels by particle flow code[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(5): 750-754.
[9] CHEN Renpeng, TANG Lujun, LING Daosheng, et al. Face stability analysis of shallow shield tunnels in dry sandy ground using the discrete element method[J]. Computers and Geotechnics, 2011, 38(2): 187-195.
[10] ZHANG Z X, HUA X Y, SCOTT K D, et al. A discrete numerical approach for modeling face stability in slurry shield tunnelling in soft soils[J]. Computers and Geotechnics, 2011, 38(1): 94-104.
[11] FANG Yong, WANG Jun, JIANG Yinchao, et al. Study on ground settlement induced by shield tunnel construction in sandy gravel stratum[C]// International Conference on Pipelines and Trenchless Technology. Wuhan: ASCE, 2013: 1567-1573.
[12] JIANG Mingjing, YIN Zhenyu. Analysis of stress redistribution in soil and earth pressure on tunnel lining by discrete element method[J]. Tunnelling and Underground Space Technology, 2012, 32(6): 251-259.
[13] JIANG Mingjing, YIN Zhenyu. Influence of soil conditioning on ground deformation during longitudinal tunneling[J]. Comptes Rendus Mecanique, 2014, 342(3): 189-197.
[14] 江英超, 何川, 方勇, 等. 盾构施工对黄土地层的扰动及管片衬砌受荷特征[J]. 中南大学学报(自然科学版), 2013, 44(7): 2934-2941.
JIANG Yinchao, HE Chuan, FANG Yong, et al. Soil disturbance caused by shield tunneling and segment lining loading characteristics in loess strata[J]. Journal of Central South University (Science and Technology), 2013, 44(7): 2934-2941.
[15] 江英超, 方勇, 何川, 等. 砂卵石地层盾构施工滞后沉降形成的细观研究[J]. 地下空间与工程学报, 2015, 11(1): 171-177.
JIANG Yinchao, FANG Yong, HE Chuan, et al. Study on delayed settlement formation induced by shield tunneling in sandy cobble strata[J]. Chinese Journal of Underground Space and Engineering, 2015, 11(1): 171-177.
[16] 王俊, 何川, 封坤, 等. 砂卵石地层中大断面泥水盾构泥膜形态研究[J]. 现代隧道技术, 2014, 51(6): 108-115.
WANG Jun, HE Chuan, FENG Kun, et al. Research on the dynamic behavior of the slurry membrane of a large section slurry shield in a sandy cobble stratum[J]. Modern Tunnelling Technology, 2014, 51(6): 108-115.
[17] 瞿同明, 王树英, 刘朋飞. 土压平衡盾构土仓排土引起的干砂地层响应分析[J]. 郑州大学学报(工学版), 2017, 38(1): 16-21.
QU Tongming, WANG Shuying, LIU Pengfei. Characteristic analysis on response of dry sand stratum due to soil extracting in EPB shield chamber[J/OL]. Journal of Zhengzhou University (Engineering Science). 2017, 38(1): 16-21.
[18] TAYLOR R N. Geotechnical centrifuge technology[M]. 1st ed. London: Chapman & Hall, 1995: 20-34.
[19] GARNIER, GAUDIN C, SPRINGMAN SM, et al. Catalogue of scaling laws and similitude questions in geotechnical centrifuge modeling[J]. International Journal of Physical Modelling in Geotechnics, 2007, 3(3): 1-23.
[20] Itasca Consulting Group. Manual of particle flow code in 2-dimension: theory and background[M]. 3.1 ed. Minneapolis: Itasca Consulting Group Inc, 2004: 9-14.
[21] CHAMBON P, CORTE J F. Sallow tunnels in cohesionless soil stability of tunnel face[J]. Journal of Geotechnical Engineering, 1994, 120(7): 1148-1164.
(编辑 伍锦花)
收稿日期:2016-12-13;修回日期:2017-01-18
基金项目(Foundation item):中国博士后科学基金项目(2015T80887);中南大学创新驱动资助项目(2015CXS015);中南大学研究生创新项目(2016zzts414) (Project(2015T80887) supported by the China Postdoctoral Science Foundation; Project(2015CXS015) supported by the Innovation Driven Projects of Central South University; Project(2016zzts414) supported by the Innovation Projects for Graduate Student of Central South University)
通信作者:王树英,博士,副教授,从事岩土与隧道相关研究;E-mail: sywang@csu.edu.cn