Forced response characteristics of bladed disks withmistuning non-linear friction
来源期刊:中南大学学报(英文版)2011年第3期
论文作者:王艾伦 龙清
文章页码:679 - 684
Key words:bladed disk; dry friction damping; random mistuning; incremental harmonic balance method; vibration localization
Abstract: Aimed at the difficulty in revealing the vibration localization mechanism of mistuned bladed disks by using simple non-linear model, a mechanical model of the bladed disk with random mistuning of hysteretic dry friction damping was established. Then, the incremental harmonic balance method was used to analyze the effects of the parameters of bladed disks, such as the mistuning strength of dry friction force, coupled strength, viscous damping ratio and friction strength, on the forced response of the bladed disks. The results show that the vibrational energy localization phenomenon turns up in the tuned bladed disks if the nonlinear friction damping exists, and the random mistuning of the dry friction force intensifies this kind of vibration localization.
J. Cent. South Univ. Technol. (2011) 18: 679-684
DOI: 10.1007/s11771-011-0747-x![]()
WANG Ai-lun(王艾伦)1, 2, LONG Qing(龙清)1, 2
1. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China;
2. State Key Laboratory of High Performance and Complex Manufacturing,
Central South University, Changsha 410083, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2011
Abstract: Aimed at the difficulty in revealing the vibration localization mechanism of mistuned bladed disks by using simple non-linear model, a mechanical model of the bladed disk with random mistuning of hysteretic dry friction damping was established. Then, the incremental harmonic balance method was used to analyze the effects of the parameters of bladed disks, such as the mistuning strength of dry friction force, coupled strength, viscous damping ratio and friction strength, on the forced response of the bladed disks. The results show that the vibrational energy localization phenomenon turns up in the tuned bladed disks if the nonlinear friction damping exists, and the random mistuning of the dry friction force intensifies this kind of vibration localization.
Key words: bladed disk; dry friction damping; random mistuning; incremental harmonic balance method; vibration localization
1 Introduction
In the bladed disks of modern turbo-machinery, the structures such as shrouding wire, shroud, surrounding strap and blade root damper are widely used to restrain the blade vibration by artificially increasing the dry friction damping of the structures. However, the dry friction damping force is non-linear [1], and the random mistuning of different blade dry friction (the dry friction of each blade is no longer identical) caused by the installation and abrasion of dampers would lead to the vibration localization. These brought a lot of problems to study the vibration characteristics of bladed disks and to design the optimal structure of dry friction damper. The difficulty mainly lays on the establishment of a nonlinear mechanical model and how to solve the nonlinear vibratory response [2].
WEI and PIERRE [3] analyzed the influence of dry friction damping on the localization of vibration resembling cycle period structure with the harmonic balance method. Then, PETROV [4-5], CIGEROGLU and OZGUVEN [6], CHA and SINHA [7] conducted researches on the forced vibratory response of bladed disks with different dry friction models. However, all the researches mentioned above did not take the mistuning of dry friction into consideration. Actually, the pressure between the friction surfaces of dampers is adjusted when they are installed, and the installation and abrasion would bring about random mistuning of pressure, leading to the random mistuning of the dry friction. PETROV and EWINS [8], WANG et al [9] studied the forced response of bladed disks with random mistuning of dry friction. However, because of the difficulty in numeric calculation, the friction studied is viscous sliding friction which is much different from the actual friction. In addition, in the past, the major method used to analyze the vibratory response of bladed disks with mistuned nonlinear dry friction was the harmonic balance method [3-4, 8-11], but it was difficult to analyze the multidimensional nonlinear problems with this method.
In this study, a dynamical model of bladed disk with randomly mistuned hysteresis nonlinear friction damping was established. And a simulation analysis was carried out to study the influence of systematical parameters like mistuning strength, coupling stiffness, viscous damping ratio and friction strength on the forced response of the bladed disks under the circumstance of random mistuning of dry friction with the IHB method [12-13], which can solve the multi-dimensional nonlinear vibration more effectively.
2 Model of mistuned bladed disk and solution of motion equation
In the bladed disks, the dry friction damping mainly exists in two forms. One is the dry friction damping of blade (B-G dry friction damping), such as the dry friction damping of listrium, where the relative location of circumferential direction between the damper and the turntable is fixed. The other is the dry friction damping between the blades (B-B dry friction damping), such as the friction damping among the shrouding wire, shroud and surrounding strap.
In this work, the vibratory response of mistuned bladed disk with B-G dry friction damping (as shown in Fig.1) was analyzed, and the vibratory response of mistuned bladed disk with the B-B dry friction damping was also discussed.
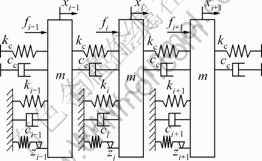
Fig.1 Model of bladed disks with B-G friction dampers
The parameters in Fig.1 are defined as follows. n is the number of blades; m is the mass of blade; ki is the stiffness of the i-th blade (ki=k when tuned); kc is the coupling stiffness between blades; ci is the viscous damping of the i-th blade (ci=c when tuned); cc is the viscous damping between blades; zi is the dry friction of the i-th blade; fi is the incentive performed on the i-th blade; ω is the frequency of the exciting force; ![]() is the inherent frequency of the tuned blade; Ω=ω/ωb, is the frequency parameter; σ is the standard deviation of mistuned items;
is the inherent frequency of the tuned blade; Ω=ω/ωb, is the frequency parameter; σ is the standard deviation of mistuned items; ![]() is the viscous damping ratio; R2=kc/k, is the coupling strength between the blades; xi is the displacement of the i-th blade.
is the viscous damping ratio; R2=kc/k, is the coupling strength between the blades; xi is the displacement of the i-th blade.
Then, the equation of vibration of the i-th blade can be illustrated as
![]()
![]() (1)
(1)
The overall equations of bladed disk can be derived as
![]() (2)
(2)
In Eq.(2), x is the column matrix of displacement; M, Cc, K, Kc, z(t) and f(t) are the quality, viscous damping of blades, viscous damping between the blades (because its influence is very small, Cc=0 is often taken), blade stiffness, coupling stiffness, nonlinear friction and column matrix of exciting force, respectively.
The air is disturbed at the non-rotating parts and rotating parts when it flows through air intake, and usually forms a harmonic exciting force on the blades. Therefore, the exciting force on the blades is often described as the harmonic force:
![]() (3)
(3)
τ=ωt, ![]() i=1, 2, 3, …, n
i=1, 2, 3, …, n
where ω is the exciting frequency, n is the number of blades, and E is the order of exciting force.
The hysteresis restoring force produced in the segment of dry friction damping is z(τ)i=z(ωt)i. If the mutation of pressure Ni of contact surface happened in the process of the blade vibration is not taken into account, the dry friction z(τ)i and the relative displacement qi would form a constitutive relation of sectional linear hysteresis line, as shown in Fig.2.

Fig.2 Corresponding hysteresis curve between friction and displacement
The relative motion between two contact surfaces is supposed to be a simple harmonic motion, that is to say, the relative displacement qi could be illustrated as
![]() (4)
(4)
where τ=ωt, qim is the steady-state relative amplitude between friction surfaces in the segment of dry friction damping of the i-th blade, and φi is the phase difference of the dry friction of the i-th blade.
Then, according to the constitutive relation in Fig.2, the mathematical expression of the hysteresis dry friction could be derived as
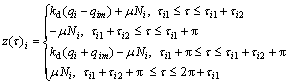 (5)
(5)
![]()
![]()
where μ is the friction coefficient between the friction surfaces, Ni is the normal pressure between the friction surfaces in the segment of the dry friction damping in the i-th blade, namely the positive pressure (Ni=N+δN, N is the pressure of harmonic system, δN is the mistuned pressure introduced), and kd is the shear stiffness between the contact surfaces.
3 Application examples and vibration localization analysis
The lumped parameter model of bladed disk with the dry friction damping (as shown in Fig.1) was used to study the vibration characteristics of a bladed disk with twelve blades under the influence of various parameters.
3.1 Vibrational energy localization of bladed disks with tuned nonlinear friction damping
Figure 3 shows the amplitude-frequency response of the tuned bladed disk with twelve blades. The X, Y, Z axes represent the ratio of exciting frequency to natural frequency of blades, serial numbers of blades (arranged according to the phase difference of exciting force) and vibration amplitude of blades, respectively.
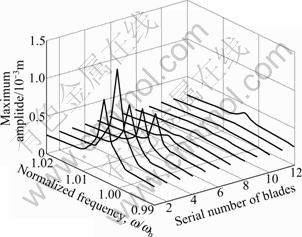
Fig.3 Amplitude-frequency curves for twelve blades of tuned bladed disk
It is known that if the amplitude-frequency responses of all the blades in linearly tuned bladed disk are identical, vibration energy localization would not emerge; in most cases, the location is caused by mistuning. But in the study of GEORGIADES et al [14-15], the localization of vibration might appear in tuned bladed disk with cubic nonlinear stiffness. As shown in Fig.3, it is known that the tuned bladed disk with nonlinear friction damping might also cause the localization of the vibrational energy. This indicates that the localization of the vibrational energy caused by the factors like nonlinear friction should also be taken into account.
3.2 Vibration characteristics of bladed disks with random dry friction mistuning
3.2.1 Influence of random mistuning strength of dry friction
Figure 4 shows the amplitude-frequency responses for the mistuned bladed disks with random dry friction. It can be noticed that the resonant amplitude of Blade 2 is the largest. In order to analyze the vibrational characteristics of the mistuned bladed disks more visually, Figs.5-9 show the amplitude-frequency response of the second blade, whose amplitude is the largest. Figure 5 shows the amplitude-frequency response under the influence of random mistuning strength of dry friction damping.
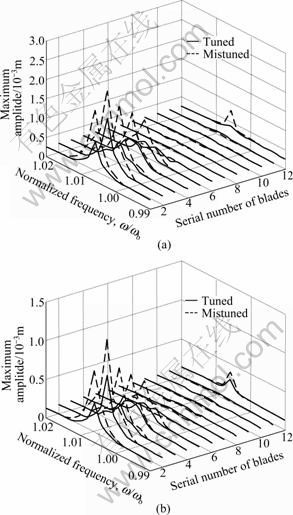
Fig.4 Amplitude-frequency curves for twelve blades of randomly mistuned bladed disks: (a) R=0.1, ζ=0.004, P=1.5; (b) R=0.1, ζ=0.008, P=1.5
Figures 4 and 5 show that the localization of vibration in the bladed disk is exacerbated with random mistuning of dry friction, and it would be further exacerbated with increasing the mistuning strength. Moreover, the mistuning also expands the resonant region and enhances the resonant frequency of the bladed disk to some extent. This indicates that the random mistuning of the dry friction restrains the vibration reduction capacity of dampers, and this capacity would be further decreased with the increase of the random mistuning strength.

Fig.5 Effect of random mistuning strength of dry friction damping on amplitude-frequency response: (a) R=0.1, ζ=0.004, P=1.5; (b) R=0.1, ζ=0.008, P=1.5
3.2.2 Influence of coupling stiffness
Figure 6 shows the influence of coupling stiffness on the largest resonant amplitude of mistuned bladed disks when the viscous damping ratio is 0, 0.004 and 0.008, respectively.
It is indicated that under different coupling stiffnesses, the influence of random dry friction mistuning on the amplitude differs sharply. The weaker the coupling stiffness is, the more sensitive the bladed disk is to random dry friction mistuning; while the random dry friction mistuning can hardly affect the bladed disk with strong coupling stiffness.
3.2.3 Influence of viscous damping ratio
Figure 7 indicates that the largest resonant amplitude of mistuned bladed disk with weak and strong coupling stiffness changes with the viscous damping ratio. Figure 8 shows the increased percentage of the largest resonant amplitude under the influence of viscous damping ratio.
In Fig.8, the amplitude magnification factor is defined as
![]() (6)
(6)
where Atuned denotes the maximum amplitude of the tuned bladed disks; Amistuned is the maximum amplitude of the mistuned bladed disks.
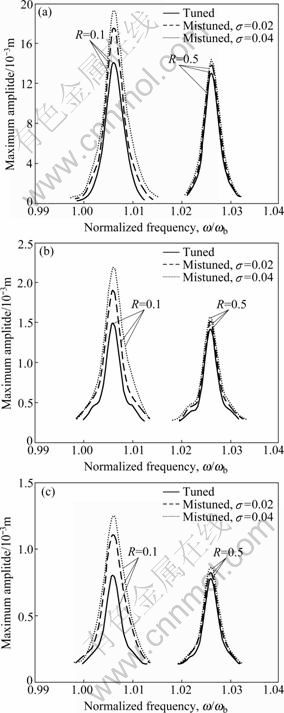
Fig.6 Effect of coupled stiffness on largest resonant amplitude of bladed disks: (a) ζ=0, P=1.5; (b) ζ=0.004, P=1.5; (c) ζ= 0.008, P=1.5
Figure 7(a) shows that in the bladed disk with weak coupling, the random dry friction mistuning reduces the restraint of viscous damping to resonant amplitude, and the bladed disk with large viscous damping is more sensitive to the random dry friction mistuning (Fig.8). While in the bladed disk with strong coupling, random dry friction mistuning hardly affects the restraint of viscous damping to the bladed disk (Fig.7(b)).

Fig.7 Effect of viscous damping ratio (ζ) on largest resonant amplitude: (a) R=0.1, P=1.5; (b) R=0.5, P=1.5
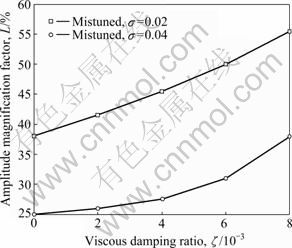
Fig.8 Increased percentage of maximum resonant amplitude under influence of viscous damping ratio
3.2.4 Influence of ratio of exciting force amplitude on friction force amplitude
Figure 9 shows the amplitude-frequency response under the influence of the ratio of exciting force amplitude to the friction force amplitude.
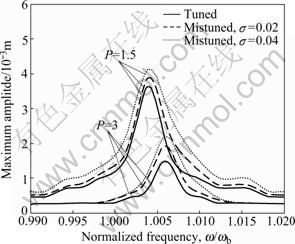
Fig.9 Effect of amplitude ratio of excitation to dry friction damping on amplitude-frequency (R=0.1, ζ=0.004)
As shown in Fig.9, with the decrease of the ratio of amplitude of exciting force to the friction force (P=f0/μN), the bladed disk is more sensitive to random dry friction mistuning, and the resonant frequency will increase (the friction enhances the equivalent stiffness). This indicates that the random dry friction mistuning mainly affects the bladed disk with larger friction, and the resonant frequency may be avoided properly through changing the friction forces.
4 Conclusions
1) The localization of vibrational energy may be caused not only by the mistuning and nonlinear stiffness, but also by the nonlinear friction damping of the tuned bladed disk.
2) The random mistuning of dry friction exacerbates the localization of harmonic bladed disk and restrains the vibration reduction capacity of friction dampers. Such vibration reduction ability will be further reduced with the increase of the random mistuning.
3) The bladed disk with weak coupling and large viscous damping ratio is more sensitive to random mistuning of dry friction, and the random mistuning of dry friction mainly affects the bladed disk with large friction.
References
[1] SINHA A, GRIFFIN J H. Effects of static friction on the forced response of frictionally damped turbine blades [J]. Journal of Engineering for Gas Turbines and Power, 1984, 106 (1): 65-59.
[2] XU Zi-li, CHANG Dong-feng, LIU Ya-lin. Forced response analysis of blade system with dry friction damper using one-bar microslip analytic model [J]. Journal of Vibration Engineering, 2008, 21(5): 505-510. (in Chinese)
[3] WEI S T, PIERRE C. Effect of dry friction damping on the occurrence of localized forced vibrations in nearly cyclic structures [J]. Journal of Sound and Vibration, 1989, 129(3): 397-416.
[4] PETROV E P. A method for use of cyclic symmetry properties in analysis of non-linear multi-harmonic vibrations of bladed disks [J]. Journal of Turbomachinery, 2004, 126(1): 175-183.
[5] PETROV E P. Method for direct parametric analysis of non-linear forced response of bladed disks with friction contact interface [J]. Journal of Turbomachinery, 2004, 126(4): 654-662.
[6] CIGEROGLU E, OZGUVEN H N. Non-linear vibration analysis of bladed disks with dry friction dampers [J]. Journal of Sound and Vibration, 2006, 295(3): 1028-1043.
[7] CHA D, SINHA A. Statistics of responses of a mistuned and frictionally damped bladed disk assembly subjected to white noise and narrow band excitations [J]. Probabilistic Engineering Mechanics, 2006, 21(4): 384-396.
[8] PETROV E P, EWINS D J. Generic friction models for time-domain vibration analysis of bladed disks [J]. Journal of Turbomachinery, 2004, 126(1): 84-192.
[9] WANG Hong-jian, HE Er-ming, YU Shi-xia. Forced response characteristics of bladed disk with disordered dry friction [J]. Journal of Aerospace Power, 2006, 21(4): 711-715. (in Chinese)
[10] CAMERON T M, GRIFFIN J H. An alternating frequency/time domain method for calculating the steady-state response of non-linear dynamic systerms [J]. Journal of Applied Mechanics, 1989, 56(1): 149-154.
[11] CARDONA A. A multiharmonic method for non-linear vibration analysis [J]. International Journal for Numerical Methods in Engineering, 1994, 37(9): 1593-1608.
[12] CHEUNG Y K, CHEN S H, LAU S L. Application of the incremental harmonic balance method to cubic non-linearity systems [J]. Journal of Sound and Vibration, 1990, 140 (2): 273-286.
[13] CHEN Shu-hui. Quantitative analysis methods for strongly nonlinear vibration system [M]. Beijing: Science Press, 2007: 171-178. (in Chinese)
[14] GEORGIADES F, PEETERS M, KERSCHEN G, GOLINVAL J C, RUZZENE M. Localization of energy in a perfectly symmetric bladed disk assembly due to nonlinearities [C]// Proceedings of IMECE2007. Washington: ASME, 2007: 229-237.
[15] GEORGIADES F, PEETERS M, KERSCHEN G, GOLINVAL J C. Modal analysis of a non-linear periodic structure with cyclic symmetry [J]. AIAA Journal, 2009, 47(4): 1014-1024.
(Edited by YANG Bing)
Foundation item: Project(2007CB707706) supported by the National Basic Research Program of China
Received date: 2010-01-27; Accepted date: 2010-08-03
Corresponding author: WANG Ai-lun, Professor, PhD; Tel: +86-731-88876764; E-mail: walwlz@sohu.com

