J. Cent. South Univ. (2016) 23: 2296-2304

DOI: 10.1007/s11771-016-3287-6

Fuzzy robust sliding mode control of a class of uncertain systems

REN Li-tong(任立通)¹, XIE Shou-sheng(谢寿生)¹, MIAO Zhuo-guang(苗卓广)²,

TIAN Hu-sen(田虎森)¹, PENG Jing-bo(彭靖波)¹

1. Aeronautics and Astronautics Engineering Institute, Air Force Engineering University, Xi’an 710038, China;

2. Beijing Aeronautical Engineering Technical Research Center, Beijing 100076, China

Central South University Press and Springer-Verlag Berlin Heidelberg 2016

Abstract: Aiming at a class of systems under parameter perturbations and unknown external disturbances, a method of fuzzy robust sliding mode control was proposed. Firstly, an integral sliding mode surface containing state feedback item was designed based on robust H_∞ control theory. The robust state feedback control was utilized to substitute for the equivalent control of the traditional sliding mode control. Thus the robustness of systems sliding mode motion was improved even the initial states were unknown. Furthermore, when the upper bound of disturbance was unknown, the switching control logic was difficult to design, and the drawbacks of chattering in sliding mode control should also be considered simultaneously. To solve the above-mentioned problems, the fuzzy nonlinear method was applied to approximate the switching control term. Based on the Lyapunov stability theory, the parameter adaptive law which could guarantee the system stability was devised. The proposed control strategy could reduce the system chattering effectively. And the control input would not switch sharply, which improved the practicality of the sliding mode controller. Finally, simulation was conducted on system with parameter perturbations and unknown external disturbances. The result shows that the proposed method could enhance the approaching motion performance effectively. The chattering phenomenon is weakened, and the system possesses stronger robustness against parameter perturbations and external disturbances.

Key words: uncertain systems; robust control; fuzzy sliding mode control; chattering

1 Introduction

Parameter perturbations and external disturbances are common phenomena in actual systems. Sufficient considerations should be taken for the above-mentioned uncertain ingredients when a controller is designed, thus the system robustness could be guaranteed. Otherwise, unpredictable performance deterioration might occur to the system, even the whole closed loop system would sink into the unstable states [1]. The control strategies research for uncertain systems involves in multiple hot areas, such as information transmission [2], chaos system [3-5], motion control [6-7], and structural vibration control [8]. Mature algorithms including robust control [9], generalized predictive control and sliding mode control were already proposed. The sliding mode control [10-12] was proved an ideal method for uncertain system control. The method has an outstanding advantage of quick response, lower requirement for model accuracy, and easy in realization of projects. More important is the truth that sliding mode control presents insensitivity to parameter perturbations and external disturbances. Consequently, it has been widely adopted in practical issues as robot control, aircraft control and motor control [13], serving as an excellent robust control strategy.

There are two phases in typical sliding mode control, the reaching phase which was defined as the motion process from the initial state to the sliding mode, and the sliding phase on the sliding mode surface. Generally speaking, the robustness of sliding mode control is only impactful during the sliding phase. However, the invariant condition is not satisfied during the reaching phase, resulting in the system’s sensitivity to uncertain factors, which would influence the control effect greatly [14-15]. To solve the problem, an advisable solution is to shorten or eliminate the reaching phase, which could drive the system state approaching the sliding mode against time. And this is the fundamental of global sliding mode control [16]. Aiming at the control of motor ABS system, Ref. [17] put forward a global sliding mode control based on RBF network. A dynamic sliding mode surface was designed, through which the system state stays on the ideal sliding mode initially. References [18] and [19] designed an integral sliding mode surface including time delay for uncertain system with state time delay and input time delay, respectively. The global robustness to uncertain was confirmed by adding time delay compensation in the controller. Reference [20] proposed a global robust sliding mode control for a class of uncertain affine nonlinear systems. The nonlinear system was transformed to a linear one using exact linearization technique. Then a global sliding mode control strategy was designed to obtain the optimal regular, through which the system exhibits global robustness to uncertainties. In the synthesis, global sliding control could eliminate the reaching phase by designing a nonlinear sliding mode surface in the form of s=Hx(t)-f(t). However, f(t) must satisfy the condition of f(0)=Hx(0), which means the initial system state should be known. Otherwise, the condition that the system state lies on the sliding mode surface initially could not be guaranteed.

Besides, sliding mode control contains the switching control item of M sgn(s), which could confirm the invariability of sliding mode control. Whereas, the value of M is somewhat difficult to define. First of all, M must be larger than the upper bound of uncertainties to achieve desirable control effect. Although the problem could be overcome by setting M large enough, severe chattering phenomenon always happens caused by overlarge switching control item [21], resulting in low control accuracy. Simultaneously, control signals switching frequently is unattainable in actual control design.

Aiming at the above mentioned issues, and enlightened by Ref. [14], a fuzzy global sliding mode control method is designed in this work. First, an integral sliding mode surface containing state feedback item is put forward based on robust H_∞ control theory and linear matrix inequality (LMI) method. The robust state feedback control is applied to take the place of equivalent control. The robustness of reaching phase is improved when the system initial state is unknown. Then the reaching phase obtains global robustness, and the control design process gets simplified meanwhile. Additionally, the fuzzy system approximation method is utilized to design a stable sliding mode controller in condition of unknown uncertain upper bound. The fuzzy control item is used to replace the switching control one. By this way, the chattering phenomenon could be improved effectively, and the control effect is desirable contemporarily. A numerical simulation is conducted on the uncertain system with parameter perturbations and external disturbances, and the result shows the effectiveness of the proposed method.

2 Robust state feedback sliding mode control design

Considering the general uncertain system as

         (1)

whereis the state variable; is the control input; is the external disturbance; andare known matrixes with corresponding dimension, and (A, B) satisfies the condition of full-controlled rank(B)=m;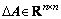and 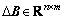are respectively the perturbation matrixes of A and B.

Assumption 1: For uncertain systems as Eq. (1), the parameter perturbations and external disturbances satisfy the matching condition, ie △A=BE_A, △B=BE_B and d=BE_d. Let

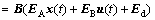
                            (2)

where is the equivalent disturbance value of the uncertain system, and is time varying and unknown. Assuming and the upper bound of disturbance L is an unknown positive constant.

Under the assumption above, system (1) is equivalent to

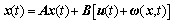                 (3)

2.1 Design of integral sliding mode surface

For uncertain systems as Eq. (1), considering the following integral sliding mode surface, it is obtained

               (4)

Theorem 1: For uncertain systems as Eq. (1) with assumption 1, if existing positive definite matrix satisfies the following linear matrix inequality defined as

then the sliding mode dynamics is asymptotic stable.

Proof: Differentiating Eq. (4) and considering Eq. (1), there is

    (5)

When the system slides on the sliding mode surface, S=0,then the equivalent control of system (1) could be achieved:

  (6)

Substituting Eq. (6) into Eq. (1) yields the sliding mode motion equation

                         (7)

From Eq. (7), we can see that the sliding mode motion is absolutely invariable to parameter perturbations and external disturbances, when the matching condition is satisfied.

Construct the Lyapunov function as

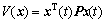                           (8)

Differentiating Eq. (8) along Eq. (7) yields

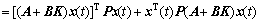
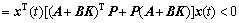   (9)

Based on the Lyapunov stability theory, the sliding mode motion will converge to equilibrium state asymptotically.

2.2 Design of state feedback sliding mode control law

Design the sliding mode control law as:

u(t)=u_K+△u                                 (10)

where △u=-(HB)^-1[η+L||HB||]sgn(S); η is a positive constant; u_K=Kx(t) is the continuous control item with the form of state feedback control.

Theorem 2: For uncertain system (1) satisfying the matching assumption 1, the integral sliding mode surface is designed as Eq. (4). Driven by the control law Eq. (10), the system could reach the sliding mode surface in finite time and maintain on it thereafter.

Proof: Define the Lyapunov function as

                          (11)

Differentiating Eq. (11) with respect to t, we obtain

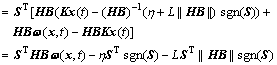
    (12)

where ||S||₁=S^Tsgn(S).

As ||S||₁≥||S||, when ||S||≠0, Eq. (12) becomes

                          (13)

Thus system (1) could reach the sliding mode surface Eq. (4) in finite time and maintain on it under the function of control law (10).

2.3 Robust state feedback matrix calculation

Equation (10) merely gives the form of control law, however, the matrix K is still an unknown parameter. Thus the following work is to calculate an appropriate state feedback matrix K. Generally speaking, system’s feedback matrix could be obtained through methods as pole assignment. Additionally, if (A, B) is controllable, the pole could be assigned arbitrarily. However, the robustness of these controllers is not under consideration. To assure the system states’ fast convergence to the ideal sliding mode surface, as well as somewhat robust to uncertain factors, a robust H_∞ state feedback control law is designed using the LMI method [22] in this work.

For Eq. (3), define the generalized controlled plant as

            (14)

where is the controlled output; C_p, D_p and H_p are constant matrixes with the corresponding dimension. The other variables share the same meaning with Eq. (3).

Here the state feedback matrix is designed applying the LMI method. By which the controller u_K=Kx(t) is designed to insure that the closed loop system (14) is asymptotically stable. And the closed-loop transfer function T_ωz(s) should meet the following expression:

                            (15)

where γ is a given positive constant. The control law u_K=Kx(t) with this quality will be called as a state feedback H_∞ control law of system (14). This is a typical robust H_∞ state feedback control problem.

Theorem 3: For system (14), there exists a state feedback matrix H_∞ controller, if and only if a symmetric positive definite matrix X and a matrix W exist, making the following matrix inequality holds

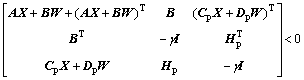 (16)

If Eq. (16) has an optimal solution (γ^*, X^*, W^*), then there exists a state feedback controller u_K=W^*(X^*)^-1x(t) making system (14) asymptotically stable, and ensuring the feasibility of H_∞ condition as Eq. (15) simultaneously.

Proof: According to robust H_∞ control theory, the closed loop system (14) is asymptotically stable and meets the robust H_∞ performance index γ, if and only if a symmetric positive definite matrix P exists, satisfying

 (17)

Using matrix diag{P^-1, I, I} for left and right multiplication with the left side of equation (17), we will get the equivalent form as:

 (18)

Substituting X=P^-1 and W=KX into inequation (18), the matrix inequality (16) is obtained. As for the solution of matrix X and W in matrix inequality (16), the mincx solver of LMI toolbox in MATLAB will be applied. And the robust state feedback controller could be obtained.

3 Fuzzy robust state feedback sliding mode controller design

The form of controller in Eq. (10) is based on the assumption that the interference upper bound L has been known. However, the actual systems are located in fairly complex environment, thus the system parameter perturbation and external disturbance are always unknown. In this circumstance, the switching control gain is somewhat difficult to set. The system could not be controlled to the stable state if the gain is set to an excessively small value. When the gain value is overlarge, the system stability could be confirmed, at the cost of severe chattering phenomenon. Aiming at the above problems, a fuzzy controller is designed here, which is utilized to take the place of switching control in Eq.(10), thus to improve the control accuracy, as well as weaken the chattering.

3.1 Fuzzy logic approximation principle

Suppose that the fuzzy system is constituted with fuzzy If-Then rules in the form:

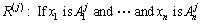
    (19)

By using strategy of product inference, singleton fuzzification and center-average defuzzification, the system output is

     (20)

whereis the membership function of the variable x_i.

Setting

                     (21)

Then Eq. (20) becomes

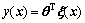                             (22)

where θ=[θ₁, θ₂, …, θ_m]^T, ξ=[ξ₁, ξ₂, …, ξ_m]^T.

3.2 Design of fuzzy robust state feedback sliding mode controller

Using the output of the fuzzy system to approximate △u in Eq.(10), then the control law Eq. (10) becomes

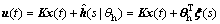         (23)

where is the output in the same form with Eq. (20); is the fuzzy vector in the same form with Eq. (21) and vector can be adjusted to the optimal according to the adaptive law.

It could be seen from the controller in Eq. (23) that the known upper bound of the uncertainty is no longer necessary. The switch term is substituted with the continuous fuzzy output and the chattering could be greatly weakened.

Set

                (24)

Theorem 4： For uncertain multivariable system (1), designing the integral sliding mode surface as Eq. (4), the control law (23) is adopted, whose parameter vector is adjusted by the following adaptive law (25), then the system will be stable

                    (25)

where 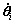is the adaptive law parameter, parameter r_i>0 is a fixed constant.

Proof: Define the optimal parameter as

             (26)

where Ω_h is the aggregation of θ_h. Then differentiating S yields

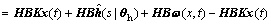
       (27)

where

Define the Lyapunov function as

              (28)

Calculating the derivative of V yields

 (29)

where 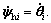Substituting Eq. (25) into Eq. (29) yields

           (30)

Since ||S||₁≥||S||, ||HB||≥1, when ||S||≠0, Eq. (30) results in

                            (31)

The system could be driven to stable system under the function of the proposed fuzzy robust sliding mode controller.

Remark 1: In control law (10), the robust state feedback control u_K(t)=Kx(t) is designed aiming at the generalized system (14), which could ensure that the controlled output z is robust to disturbance value ω in some degree. As the sliding mode surface S is also a function of the system state x, S is more insensitive to ω under the control of u_K(t). Consequently, the anti- jamming capability of reaching phase is improved. And the reaching phase is global robust even the initial system state is unknown.

Remark 2: When the fuzzy control item is applied to replace the switching control item, the control input is defined as a continuous one based on the approximation ability of fuzzy logic. And the chattering phenomenon could be weakened greatly. Meanwhile, the known disturbance upper bound is no longer a necessary condition during the design of controller. The fuzzy role in this work takes the sliding mode surface S as the input, and the output is the fuzzy control u_F(t).

4 Numerical simulations

Consider the following uncertain system in the form of Eq. (1):

                   (32)

Firstly, the robust state feedback matrix K should be solved. Choose the parameter of the generalized system (14) as

Then the mincx solver is used to solve the following minimization problem:

min γ

s.t. X>0

₍₃₃₎

We can get γ=0.0074,

According to Theorem 1, a matrix P could be obtained using the feasp solver, which is

It is obvious that P>0, the Theorem 1 holds for the previous matrix K.

Defining the parameter H in Eq. (4) as H is nonsingular obviously, and ||HB||=1.6156>1. Defining the membership function of S as

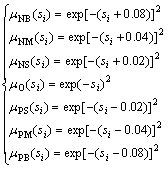                 (34)

where the adaptive parameters are set as r_i=6, i=1, 2, and the initial value of fuzzy system parameter is i=1, 2.

Defining the system disturbance parameter as

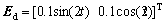
That is

 (35)

An uncertain system satisfying the matching condition is defined based on Eq. (32) and Eq. (35). The control effect of controller (23) and controller (10) will be respectively validated next. Parameters in control law (10) are chosen as η=0.1, L=0.6.

Remark 3: It can be deduced from Eq. (35) that

|||ω(x,t)||≤||E_A|| ||x(t)||+||E_B|| ||u(t)||+||E_d||≤0.3||x(t)||+ 0.2||u(t)||+0.1   (36)

As ||x(t)|| and ||u(t)|| are unknown, it is difficult to get the exact value of disturbance upper bound L. To avoid serious chattering engendered from an oversized L, a more conservative value is assigned.

The initial value is set as x(0)=[1 1]^T. The simulation results are shown in Figs. 1-4. Controller 1 represents the proposed fuzzy robust sliding mode controller (23). Controller 2 represents the traditional integral sliding mode controller (10). The results show that both of the selected controllers could drive the system to the stable state in finite time. However, Fig. 4 shows that an obvious high-frequency exists in thecontrol input of Controller 2, which derives from the discontinuous switching control item. And the situation is much better for Controller 1. As the fuzzy control item endues the control inputs with a continuous format, the chattering is eliminated effectively. It should also be noticed that the convergence procedure of the sliding mode S and system states is somewhat slower than that of Controller 2. The reason is that adaptive law (25) needs some time to reach the optimal value, on which an ideal approximation result could be acquired. The dynamic performance of the system may be influenced in some degree during the process of parameter adjusting.

Fig. 1 Changing curve of sliding surface

Fig. 2 Curve of states response

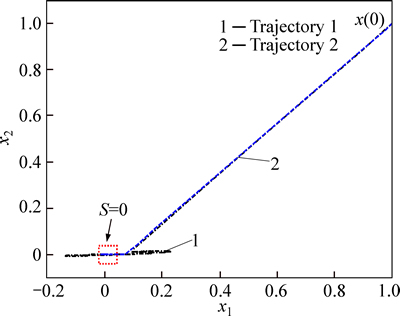
Fig. 3 Curve of system phase trajectory

Fig. 4 Changing curve of control inputs

In order to validate the control effect of the proposed robust state feedback control, the pole assignment method is used to get the state feedback matrix K_p in Eqs. (23) and (10), thus two new controllers could be obtained

u₃(t)=K_px(t)+-(HB)^-1[η+L||HB||]sgn(S) =K_px(t)+△u           (37)

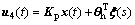                      (38)

The pole values are set as -5 and -1, then the matrix K_p could be assigned as

The other parameters remain the same as before. Four control laws (control law (23)[Controller 1], control law (10)[Controller 2], control law (37)[Controller 3], control law (38)[Controller 4]) are adapted on the uncertain system. And the convergence curve of sliding mode S is shown in Figs. 5 and 6. As depicted in the figures, the convergence procedure of Controller 1 is better than Controller 3, and the convergence procedure of Controller 2 is better than Controller 4. The results above show the advantage of robust H_∞ design method over the pole assignment method. According to the adaptive control theory, when (A, B) is absolutelycontrollable, system poles could be assigned arbitrarily. Thus the matrix K satisfying the robustness condition could also be obtained using the pole assignment method. But the selection of target pole is quite unquestioning. However, the design of matrix K could be simplified greatly while the system robustness is guaranteed.

Fig. 5 Changing curve of S₁ under different control laws

Fig. 6 Changing curve of S₂ under different control laws

To verify the controllers’ robustness to uncertain disturbance, redefining

E_d=[sin(2t) cos(2t)]^T

The other parameters remain the same as before. Simulation results are shown from Fig. 7 to Fig. 9. When the disturbance upper bound increases, the proposed method could still achieve ideal effects. The sliding mode S and system states could converge in finite time. And there is no chattering phenomenon in the control inputs. For the sake of traditional integral sliding mode controller, the disturbance upper bound has changed while the controller parameters are fixed, thus the control effect is influenced. From Figs. 7 and 8, it could be seen that oscillation has occurred in S and state value. Consequently, it could be deduced that when the disturbance upper bound is unknown, the traditional integral sliding mode control has a poor robustness to uncertain factors.

Fig. 7 Changing curve of sliding surface

Fig. 8 Curve of states response

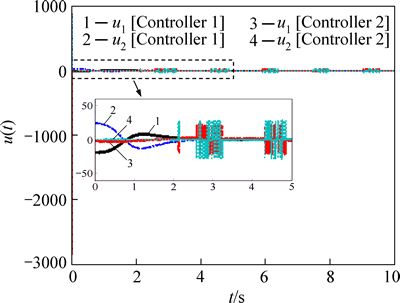
Fig. 9 Changing curve of control inputs

5 Conclusions

Aiming at a class of uncertain systems containing parameter perturbations and external disturbances, a fuzzy robust sliding mode control method is proposed based on robust control theory and fuzzy approximation method.

1) The state feedback matrix ensuring the system’s robustness to unknown uncertainties is designed based on the robust H_∞ method. As matrix K could be figured out using the LMI toolbox of MATLAB, the controller design procedure is simplified greatly. Additionally, the LMI method is more specialized than pole assignment method, the controller’s robustness is more easily to be achieved.

2) The fuzzy control designed using fuzzy system approximation method is employed to replace the switching control. Then the controller design will not rely on the disturbance upper bound L any more. The fuzzy robust sliding mode controller is achieved integrating the robust state feedback controller and the fuzzy controller. The former could improve system’s robustness to uncertain factors. And the latter could reduce the impact of disturbance upper bound change on control effect. The proposed controller is appropriate for uncertain systems satisfying the matching condition. The controller could ensure the systems’ stabilization in finite time even if the disturbance upper bound is unknown. The chattering phenomenon could also be weakened effectively, thus the proposed controller is more practical.

3) As for the fuzzy control item, a certain amount of time is required for the parameter adjusting of adaptive law. During the adjusting process, the controller parameters are not optimal, which will affect the system dynamic performance. More meticulous research will be conducted on the membership and adaptive law parameter design of the fuzzy control in future works. And the further improvement of the control performance is hopeful.

References

[1] SANJOY M, CHITRALEKHA M. Chattering free adaptive multivariable sliding mode controller for systems with matched and mismatched uncertainty [J]. ISA Transactions, 2013, 52: 335-341.

[2] ROBERT S, DOUGLAS L, PETER W. An adaptive AIMD congestion control protocol for communication networks [J]. Networking, 2004, 3042: 699-711.

[3] WU Xue-li, LIU Jie, ZHANG Jian-hua, WANG Ying. Synchronizing a class of uncertain and variable time-delay fractional-order hyper- chaotic systems by adaptive sliding robust mode control [J]. Acta Phys Sin, 2014, 63(16): 160507. (in Chinese)

[4] ZHANG Xu-xi, LIU Xian-ping, ZHU Qi-dan. Adaptive chatter free sliding mode control for a class of uncertain chaotic systems [J]. Applied Mathematics and Computation, 2014, 232: 431-435.

[5] MEHDI R, BIJAN R S, TSUNG-CHIH L. Adaptive sliding mode control in a novel class of chaotic systems [J]. Commun Nonlinear Sci Numer Simulat, 2010, 15: 4158-4170.

[6] CHEN Zhi-mei, MENG Wen-jun, ZHANG Jing-gang. Intelligent anti-swing control for bridge crane [J]. Journal of Central South University, 2012, 19: 2774-2781.

[7] MOHAMMAD M F, SAEED K. Robust control of electrically driven robots by adaptive fuzzy estimation of uncertainty [J]. Nonlinear Dyn, 2012, 69: 1465-1477.

[8] LIU Lei, WANG Ben-li. Multi objective robust active vibration control for flexure jointed struts of stewart platforms via H_∞ and μ synthesis [J]. Chinese Journal of Aeronautics, 2008, 21: 125-133.

[9] IAN R P, ROBERTO T. Robust control of uncertain systems: Classical results and recent developments [J]. Automatica, 2014, 50: 1315-1335.

[10] NAVID N, MEHDI R, ZOLGHADRI J. Adaptive fuzzy sliding mode control scheme for uncertain systems [J]. Commun Nonlinear Sci Numer Simulat, 2009, 14: 3978–3992.

[11] LIU Shuang, CHEN Li-qun. Chaos synchronization of a chain network based on a sliding mode control [J]. Chin Phys B, 2013, 22(10): 100506.

[12] LIU Jin-kun, SUN Fu-chun. Research and development on theory and algorithms of sliding mode control [J]. Control Theory and Applications, 2007, 24(3): 407-418. (in Chinese)

[13] YAO Qiong-hui, HUANG Ji-qi, WU Han-song. Variable structure control system [M]. Chongqing: Chongqing University Press, 1997: 7-9. (in Chinese)

[14] LIU Jin-kun, SUN Fu-chun. Global sliding mode control with adaptive fuzzy chattering free method for nonlinear system [C]// IMACS Multiconference on Computational Engineering in Systems Applications. Beijing, China, 2006: 541-546.

[15] LIU Yun-feng, YANG Xiao-gang, MIAO Dong, YUAN Run-ping. Chaotic synchronization problem of finite-time convergence based on fuzzy sliding mode [J]. Acta Phys Sin, 2007, 56(11): 6250-6257. (in Chinese)

[16] LIU Lei-po, HAN Zheng-zhi, LI Wen-lin. Global sliding mode control and application in chaotic systems [J]. Nonlinear Dyn, 2009, 56: 193-198.

[17] JING Yuan-wei, MAO Yan-e, GEORGI M D, ZHENG Yan, ZHANG Si-ying. Adaptive global sliding mode control strategy for the vehicle antilock braking systems [C]// 2009 American Control Conference. St. Louis, MO, USA, 2009: 769-773.

[18] LI Xiao-qian, JING Li, LIU Chang. Global sliding mode control for uncertain linear systems with state time-delays [C]// Proceedings of the 29th Chinese Control Conference. Beijing, China, 2010: 2234-2239.

[19] LI Xiao-qian, JING Li. Global sliding mode control for uncertain linear systems with input time-delays [C]// Proceedings of the 8th World Congress on Intelligent Control and Automation. Ji’nan, China, 2010: 838-842.

[20] PANG Hai-ping, CHEN Xia. Global robust optimal sliding mode control for uncertain affine nonlinear systems [J]. Journal of Systems Engineering and Electronics, 2009, 20(4): 838-843.

[21] FENG Yong, HAN Feng-ling, YU Xing-huo. Chattering free full- order sliding-mode control [J]. Automatica, 2014, 50: 1310-1314.

[22] WANG Juan, ZHANG Tao, XU Guo-kai. Theory and application of robust control [M]. Beijing, China: Publishing House of Electronics Industry, 2011: 178-191. (in Chinese)

(Edited by FANG Jing-hua)

Foundation item: Project(51476187) supported by the National Natural Science Foundation of China

Received date: 2015-04-28; Accepted date: 2015-09-17

Corresponding author: REN Li-tong, PhD; Tel: +86-18192502997; E-mail: ren_tt521@163.com