自锚式悬索桥地震响应及减震控制分析
宋旭明,戴公连,曾庆元
(中南大学 土木建筑学院,湖南 长沙,410075)
摘 要:以长沙三汊矶湘江大桥为研究对象,对自锚式悬索桥的动力特性、地震响应及粘滞阻尼器的减震效果进行分析。基于结构非一致激励地震动方程,建立空间非线性有限元模型,探讨一致输入、行波输入下结构的地震响应。分别以主梁纵向位移、塔底内力为控制目标,研究粘滞阻尼器参数变化对结构减震效果的影响。计算结果表明:地震作用下塔底顺桥向弯矩达117.492 MN?m,对自锚式悬索桥的设计起控制作用;行波效应使得主梁跨中横向位移增大90%,横向弯矩减小60%;结构纵向位移及塔底内力在考虑行波效应后减小10%左右,安装参数合理的阻尼器使主梁纵向位移减小83%,塔底纵向弯矩减小62%,达到良好的减震效果。
关键词:自锚式悬索桥;地震响应;行波效应;粘滞阻尼器
中图分类号:U448.25 文献标识码:A 文章编号:1672-7207(2009)04-1079-07
Seismic response analysis and control of
self-anchored suspension bridge
SONG Xu-ming, DAI Gong-lian, ZENG Qing-yuan
(School of Civil and Architectural Engineering, Central South University, Changsha 410075, China)
Abstract: Taking the project of Sanchaji Bridge as object, the dynamic characteristics and seismic response of self-anchored suspension bridge was calculated. The seismic response after installing viscous dampers was analyzed. Based on the equation of multi-support excitation, a spatial nonlinear finite element model was established and the seismic response of the bridge under synchronous excitation and traveling seismic excitation were discussed. In order to reduce the longitudinal displacement of the girder and the inner force of the pylon bottom, parameters of the viscous damper was studied. The results show that transverse displacements in mid-span increase by 90% and the transverse moment reduces by 60% under traveling seismic excitation. The longitudinal displacement and inner force of the pylon bottom reduces about 10% considering the effect of the traveling seismic excitation. The longitudinal displacement of the girder reduces by 83% and longitudinal moment of the pylon bottom reduces by 62% through installing viscous damper with appropriate parameters. The seismic response can be controlled effectively.
Key words: self-anchored suspension bridge; seismic response; traveling seismic excitation; viscous damper
自锚式悬索桥以其结构新颖、对地形及地质状况适应性强等优点越来越受到工程界的广泛关注,成为城市有效的桥型方案。自锚式悬索桥主缆锚固于加劲梁上,形成纵向自平衡体系,其受力体系及施工方法均与地锚式悬索桥有很大差别[1-3]。为了减小温度效应,平衡塔柱受力,双塔自锚式悬索桥一般采用纵向飘浮体系。在纵向地震作用下,主梁将产生较大的纵向位移,塔底承受的弯矩也很大。因此,通过对结构的动力特性进行分析,采用合理的计算模型得到地震作用下结构的位移及内力响应,并寻求有效的减震措施成为自锚式悬索桥抗震设计的主要工作。在各种减震控制技术中,采用阻尼减震技术,能够提高结构阻尼,抑制地震响应,在实际工程中得到广泛应用[4]。设置粘滞阻尼器为控制结构地震响应提供了一个实用而简便的方法,但必须合理选择粘滞阻尼器参数。长沙三汊矶湘江大桥是跨径组合为(70+132+328+132+ 70) m的双塔钢主梁自锚式悬索桥,桥宽为33.0 m,主跨矢跨比为1/5,吊索间距为9.0 m,桥塔高为104.2 m。本文作者以三汊矶大桥为工程背景,建立空间非线性有限元模型,计算自锚式悬索桥的动力特性,并基于结构非一致激励地震动方程,探讨一致输入、行波输入下结构的地震响应。以主梁纵向位移、塔底内力为控制目标,设置粘滞阻尼器对结构进行减震控制,并通过参数分析方法得到合理的阻尼器参数。
1 自锚式悬索桥动力特性分析
桥梁自振频率、振型等动力特性与结构的地震反应密切相关,通过桥梁动力特性的计算,确定合理的计算模式,是进行地震响应计算的基础。
1.1 空间有限元模型
利用通用有限元程序ANSYS建立三汊矶大桥空间有限元模型,采用全桥脊梁模式。主梁、桥塔及桥墩采用空间梁单元进行模拟,主缆及吊索采用只受拉的杆单元,桥面二期恒载及箱梁内压重块分别用附加质量及质量单元进行模拟[5-6]。考虑到主缆索段垂度的影响,主缆弹性模量用Ernst公式修正。由静力计算及文献[7]可知,该桥桩基刚度较大,桩-土相互作用对桥梁动力特性影响很小,因此,将桩基础模拟成固结。主梁与桥塔及桥墩横桥向位移均进行耦合,主梁与桥塔、桥墩间顺桥向均可自由滑动。三汊矶大桥空间有限元模型如图1所示。
图1 三汊矶大桥空间有限元模型
Fig.1 Spatial FE model of Sanchaji Bridge
1.2 动力特性计算结果
对于几何非线性效应突出的大跨度悬索桥,索的初始应力对桥梁的平衡构形有很大的影响,进而影响桥梁的自振特性。因此,在动力分析前,必须进行恒载状态下的非线性迭代计算,通过调整主缆及吊索的初张力,获得合理的成桥状态及结构刚度矩阵,然后,进行动力特性及地震响应计算。对桥梁前100阶振型及相应频率进行计算,表1所示为前10阶振型及其相应频率。
表1 前10阶振型及频率
Table 1 The first 10 modes and natural frequency
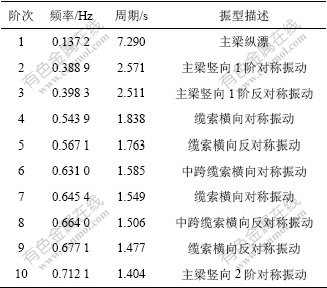
计算结果表明,由于桥梁纵向联系较弱,第1阶振型为主梁纵漂,周期为7.29 s。自锚式悬索桥主梁承受主缆巨大的水平力,使得主梁的切线刚度降低。以主梁竖向振动为主的振型较早出现,第2,3,10和25阶振型均为主梁竖向振动。缆索的振型数量较多,第4~9,13,14,16和17阶等均为缆索振动。以桥塔和桥墩为主的振动出现较晚,桥塔顺桥向振动出现在第15阶。由于主梁扭转刚度较大,一阶扭转振型出现在第40阶。
桥梁的频谱分布密集,缆索的振型所占数量较多,因此,前100阶振型对顺桥向总有效振型贡献率为83.2%,对横桥向总有效振型贡献率为87.3%,对竖向总有效振型贡献率仅为28.9%。若期望竖向总振型贡献率大于90%,则需要前800阶振型参与。振型贡献率在一定程度上反映了振型在地震反应中所占的比 例[6-7],我国《公路工程抗震设计规范》(JTJ 004—89)对此尚无相关条款,但《建筑抗震设计规范》(GB 50011—2001)、欧洲规范EUROCODE8均规定总振型贡献率应大于90%。若采用反应谱进行抗震计算,则为了获得较高的计算精度,必须计入更多的振型并采用CQC组合。
2 结构非一致地震动方程及地震波
2.1 结构非一致地震动方程
采用集中质量法,桥梁结构非一致地震动方程可表示为[8-9]:

基于拟静力位移的概念,多点激励下的总结构反应位移可分离为动力反应位移和拟静力位移,即

对于给定地面运动位移[Xb],拟静力位移[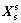 ]可由下式求得:
]可由下式求得:
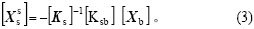
忽略由于支承运动速度[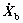 ]产生的阻尼力,式(1)可简化为:
]产生的阻尼力,式(1)可简化为:

由式(3)和(4)可分别求得拟静力位移和动力位移,然后,由式(2)得到结构总位移。
2.2 地震波
根据《长沙市三汊矶湘江大桥地质勘察报告》,三汊矶湘江大桥位于华南地震区北部、江汉地震带东南隅,处于地震烈度区划图的Ⅵ度区。考虑到特大桥梁其设防烈度可提高1度,因此,取基本烈度为7度,水平基本地震加速度峰值为0.10g(1g=9.8 m/s2)。场地类别为建筑Ⅱ类场地,设计地震分组为第1组,场地特征周期为0.35 s。缆索承重桥梁的实测阻尼比多为0.5%~1.5%。参照文献[8],取阻尼比为1.0%。由于《公路工程抗震设计规范》小于0.1 s的谱值空缺,实际计算时参照《建筑抗震设计规范》对标准反应谱进行适当调整,将其作为合成人工地震波的目标反应 谱[10-12]。利用具有变幅值三角级数迭加的非平稳随机过程数学模型,生成满足设计要求的地震波。图2所示为生成的1条人工地震波。

图2 地震加速度时程
Fig.2 Acceleration time history under earthquake
3 动力时程分析计算结果
对三汊矶大桥进行地震时程响应分析时考虑2种地震波的输入模式,即一致输入和行波输入。根据地质勘察报告,取波速分别为500,800和1 000 m/s,考虑顺桥向和横桥向分别输入,研究结构地震响应的变化情况。采用时域内逐步积分的Newmark 无条件稳定隐式积分方法, 时间步长取0.02 s , 每步迭代次数为50。考虑到结构响应相对于地震激励滞后,将进行时程分析的地震波延长至25 s,以保证获得结构的最不利响应。
3.1 顺桥向地震响应
地震波顺桥向输入时,结构控制截面的最大位移和最不利内力响应如表2所示。图3和图4所示分别为一致激励和波速为500 m/s时主梁纵向位移和塔底顺桥向弯矩的时程曲线。从表2及图3和图4可以看到:
表2 顺桥向输入时结构位移及内力响应
Table 2 Displacement and force response under longitudinal earthquake action
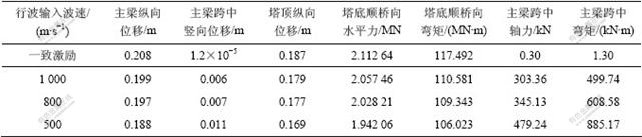
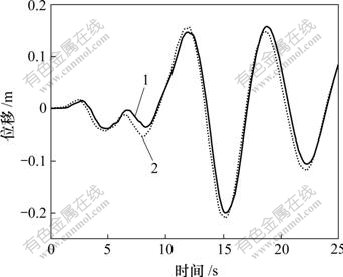
1—一致激励;2—波速500 m/s
图3 主梁纵向位移时程
Fig.3 Longitudinal displacement time history of main girder
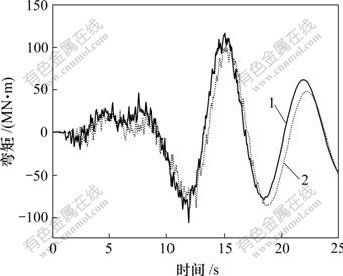
1—一致激励;2—波速500 m/s
图4 塔底顺桥向弯矩时程
Fig.4 Moment time history in pylon bottom
a. 在一致激励地震作用下,主梁纵向位移为0.208 m,塔底顺桥向弯矩达117.492 MN?m,对自锚式悬索桥的设计起控制作用,应采取有效的减震措施。
b. 考虑行波效应后,随着波速降低,主梁及塔顶纵向最大位移有减小的趋势,波速为500 m/s时纵向位移比一致激励时减小约9.6%;主梁跨中竖向位移则有所增大,但其值较小。
c. 随着波速降低,塔底顺桥向水平力及弯矩均减小,波速为500 m/s时塔底内力比一致激励时约减小10%;主梁跨中轴力及弯矩则增长明显,但其量很小,对结构设计影响不大。
3.2 横桥向地震响应
地震波横桥向输入时,结构控制截面的最大位移和最不利内力响应如表3所示。可见:
表3 横桥向输入时结构位移及内力响应
Table 3 Displacement and force response under longitudinal earthquake action
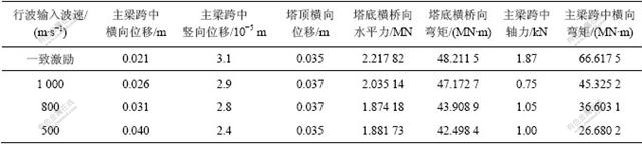
a. 由于结构横向刚度较大,地震波横桥向输入时主梁横向最大位移为0.04 m。行波效应对塔顶横桥向位移的影响很小,但对主梁横向位移的影响较大,波速为500 m/s时主梁跨中横向位移为一致激励时的1.9倍。
b. 考虑行波效应后塔底横向水平力和弯矩均有所减小,波速为500 m/s时塔底内力比一致激励时减小约15%。
c. 地震波横桥向输入时主梁跨中轴力很小,可以忽略。主梁跨中横向弯矩在一致激励时达到最大值66.617 5 MN?m,由于主梁横向抵抗矩较大,横向弯矩并不控制设计。考虑行波效应后其值显著减小,波速为500 m/s时跨中横向弯矩仅为一致激励时的40%。
4 纵向减震控制分析
在地震作用下,主梁纵向位移和塔顶顺桥向弯矩均较大。为了减小地震作用下结构的位移及内力,通过在主梁与2个桥塔间设置粘滞阻尼器对结构的地震响应进行控制。每个桥塔处横桥向设置2个阻尼器,间距为22.8 m,全桥共置4个阻尼器。
4.1 液体粘滞阻尼器参数选择
液体粘滞阻尼器是一种柱状孔隙式阻尼装置,所提供的阻尼力取决于活塞的运动速度。阻尼力F与活塞运动速度v的关系为[13-14]:
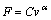 。 (5)
。 (5)
式中:C为阻尼系数;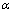 为速度指数,其常用值为0.3~1.0。在ANSYS有限元计算模型中,选择具有非线性阻尼特性的COMBIN37单元对粘滞阻尼器进行模拟。
为速度指数,其常用值为0.3~1.0。在ANSYS有限元计算模型中,选择具有非线性阻尼特性的COMBIN37单元对粘滞阻尼器进行模拟。
由式(5)可知,阻尼器参数C和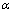 的变化对结构响应有一定影响。在计算过程中,对液体粘滞阻尼器进行参数分析,速度指数
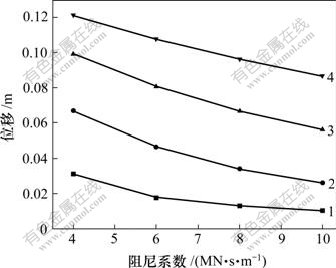
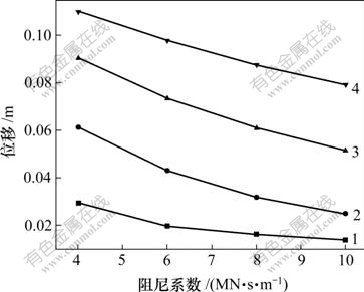
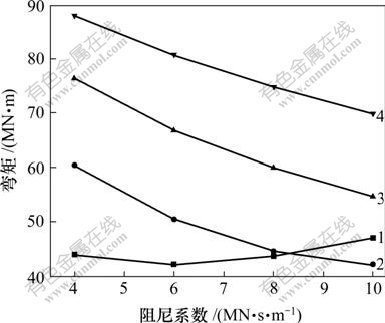
的变化对结构响应有一定影响。在计算过程中,对液体粘滞阻尼器进行参数分析,速度指数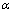 取值范围为0.4~1.0,步长为0.2,阻尼系数C的取值范围为4~10 MN?s/m,步长取2 MN?s/m。主梁纵向位移、塔顶纵向位移、塔底顺 桥向剪力及弯矩最大值随参数的变化情况如图5~8 所示。
取值范围为0.4~1.0,步长为0.2,阻尼系数C的取值范围为4~10 MN?s/m,步长取2 MN?s/m。主梁纵向位移、塔顶纵向位移、塔底顺 桥向剪力及弯矩最大值随参数的变化情况如图5~8 所示。
速度指数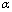 : 1—0.4; 2—0.6; 3—0.8; 4—1.0
: 1—0.4; 2—0.6; 3—0.8; 4—1.0
图5 主梁纵向位移
Fig.5 Longitudinal displacement of girder
速度指数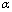 : 1—0.4; 2—0.6; 3—0.8; 4—1.0
: 1—0.4; 2—0.6; 3—0.8; 4—1.0
图6 塔顶纵向位移
Fig.6 Longitudinal displacement of pylon top
速度指数 : 1—0.4; 2—0.6; 3—0.8; 4—1.0
: 1—0.4; 2—0.6; 3—0.8; 4—1.0
图7 塔底纵向剪力
Fig.7 Longitudinal shearing force of pylon bottom
速度指数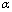 : 1—0.4; 2—0.6; 3—0.8; 4—1.0
: 1—0.4; 2—0.6; 3—0.8; 4—1.0
图8 塔底纵向弯矩
Fig.8 Longitudinal moment of pylon bottom
从图5~8可以看到,随着阻尼系数的增加,主梁及塔顶纵向位移均减小,结构的纵向变形接近于塔梁固结的变形。随着速度指数的增大,主梁及塔顶纵向位移均增大。这是因为地震作用时桥塔和主梁间的相对速度远小于1.0 m/s,因此,阻尼器的出力随其速度指数增大而减小。对于塔底纵向剪力及弯矩,其值随阻尼系数的变化不是单调变化。综合考虑结构位移、内力及阻尼器出力等因素,确定采用阻尼系数为8 MN?s/m,速度指数为0.6的阻尼器。
4.2 控制截面减震效果
选定阻尼器参数C和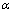 后,减震前、后主梁纵向位移及塔底顺桥向弯矩的时程曲线如图9和图10所示。
后,减震前、后主梁纵向位移及塔底顺桥向弯矩的时程曲线如图9和图10所示。
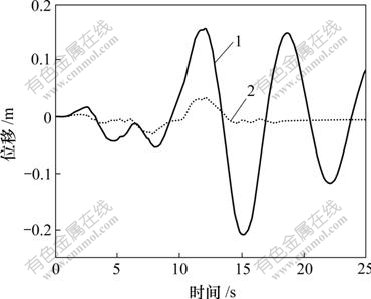
1—减震前;2—减震后
图9 主梁纵向位移时程
Fig.9 Longitudinal displacement time history
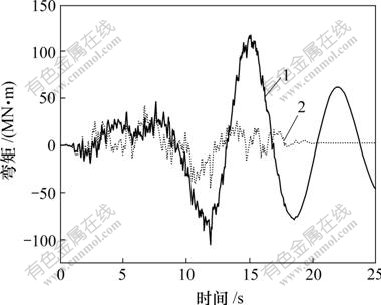
1—减震前;2—减震后
图10 塔底纵向弯矩时程
Fig.10 Longitudinal moment time history
图9和图10表明,采用粘滞阻尼器在地震过程中有效地减小了结构纵向位移和塔底纵向弯矩,达到了良好的减震效果。定义减震率f的计算公式为:
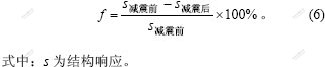
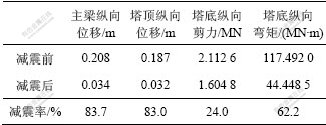
各控制参数减震前、后的最大响应值及减震率如表4所示。
从表4可以看到,安装阻尼器后,主梁及塔顶纵向位移的减震率为83%,塔底纵向弯矩减小62%,塔底纵向剪力的减小幅度也达到24%。
表4 减震前后结构响应
Table 4 Seismic Response before and after damping
5 结 论
a. 自锚式悬索桥频谱分布密集,缆索的振型所占数量较多,采用反应谱进行抗震计算时应充分衡量计入的振型数量,以满足总的振型贡献率的要求。
b. 考虑行波效应后,主梁及塔顶纵向位移有减小的趋势,但其减小幅度不大。行波效应对塔顶横桥向位移的影响不大,但对主梁跨中横桥向位移有较大影响,波速为500 m/s时跨中横向位移为一致激励时的1.9倍。
c. 在地震作用下,塔底内力尤其是塔底顺桥向弯矩响应较大,但行波效应对其影响较小。地震波横桥向输入时主梁跨中横向弯矩较大,考虑行波效应后其值显著减小。
d. 随着阻尼系数增加,结构的纵向位移接近于塔梁固结的纵向位移,主梁及塔顶纵向位移均减小;随速度指数的增大,阻尼器的出力减小,主梁及塔顶纵向位移均增大。
e. 选择参数合理的粘滞阻尼器能够有效地控制结构位移及内力,达到减小结构地震响应的目的。
参考文献:
[1] 张元凯, 肖汝诚, 金成棣. 自锚式悬索桥的设计[J]. 桥梁建设, 2002, 22(5): 30-32.
ZHANG Yuan-kai, XIAO Ru-cheng, JIN Cheng-di. Design of self-anchored suspension bridge[J]. Bridge Construction, 2002, 22(5): 30-32.
[2] 张 哲. 混凝土自锚式悬索桥[M]. 北京: 人民交通出版社, 2005.
ZHANG Zhe. Self-anchored concrete suspension bridge[M]. Beijing: China Communications Press, 2005.
[3] John A O, David P B. Self-anchored suspension bridges[J]. Journal of Bridge Engineering, 1999, 4(3): 151-156.
[4] 吴斌暄, 王 磊, 王歧峰. 使用非线性粘滞阻尼器的桥梁在地震反应中的响应分析[J]. 公路交通科技, 2007, 24(10): 76-80.
WU Bin-xuan, WANG Lei, WANG Qi-feng. A method of seismic response analysis for bridge with nonlinear viscous damper[J]. Journal of Highway and Transportation Research and Development, 2007, 24(10): 76-80.
[5] 郝南海, 王全聪. 等径侧向挤压变形均匀程度的有限元分析[J]. 中国有色金属学报, 2001, 11(2): 230-233.
HAO Nan-hai, WANG Quan-cong. Finite element analysis of deformation uniformity of equal cross section lateral extrusion[J]. The Chinese Journal of Nonferrous Metals, 2001, 11(2): 230-233.
[6] 陈仁福. 大跨悬索桥理论[M]. 成都: 西南交通大学出版社, 1994.
CHEN Ren-fu. Theory of long-span suspension bridge[M]. Chengdu: South-West Jiaotong University Press, 1994.
[7] 刘忠平. 三汊矶湘江大桥自锚式悬索桥地震反应研究[D]. 中南大学土木建筑学院, 2007.
LIU Zhong-ping. Study on seismic response of Sanchaji Xiangjiang Self-Anchored Bridge[D]. School of Civil and Architectural Engineering, Central South University, 2007.
[8] 范立础, 胡世德, 叶爱君. 大跨度桥梁抗震设计[M]. 北京: 人民交通出版社, 2001.
FAN Li-chu, HU Shi-de, YE Ai-jun. Aseismic design of large-span bridge[M]. Beijing: China Communication Press, 2001.
[9] 陆铁坚, 李 芳, 余志武. 在地震动水平与摇摆分量作用下高层结构随机地震反应[J]. 中南大学学报: 自然科学版, 2006, 37(3): 623-627.
LU Tie-jian, LI Fang, YU Zhi-wu. Random response of high-layer structures in combined action of horizontal and rocking ground motions[J]. Journal of Central South University: Science and Technology, 2006, 37(3): 623-627.
[10] 丰 硕, 项贻强, 谢 旭. 超大跨度悬索桥的动力特性及地震反应分析[J]. 公路交通科技, 2005, 22(8): 31-35.
FENG Shuo, XIANG Yi-qiang, XIE Xu. Dynamic characteristics and multi-support seismic response analysis of a super-large-span suspension bridge[J]. Journal of Highway and Transportation Research and Development, 2005, 22(8): 31-35.
[11] Abdel G A M, Rubin L I. Lateral earth-quake response of suspension bridges[J]. Journal of Structural Engineering, 1983, 109(3): 664-675.
[12] 张 卉, 王志清, 彭元诚, 等. 四渡河大跨悬索桥空间地震响应分析[J]. 地震工程与工程振动, 2007, 27(3): 70-76.
ZHANG Hui, WANG Zhi-qing, PENG Yuan-cheng, et al. Spatial seismic response analysis of long-span suspension bridge across Sidu River[J]. Journal of Earthquake Engineering and Engineering Vibration, 2007, 27(3): 70-76.
[13] Nicos M, Constantinous M C, Dargush G F. Analytical model of viscoelastic fluid dampers[J]. Journal of Structural Engineering, 1993, 119(11): 3310-3325.
[14] 王志强, 胡世德, 范立础. 东海大桥粘滞阻尼器参数研究[J]. 中国公路学报, 2005, 18(3): 37-42.
WANG Zhi-qiang, HU Shi-de, FAN Li-chu. Research on viscous damper parameters of Donghai Bridge[J]. China Journal of Highway and Transport, 2005, 18(3): 37-42.
收稿日期:2008-09-10;修回日期:2008-12-09
基金项目:国家自然科学基金资助项目(50078006)
通信作者:宋旭明(1974-),男,湖南醴陵人,博士,讲师,从事桥梁抗震及极限承载力研究;电话:0731-82656635;E-mail: ctysxm@163.com