J. Cent. South Univ. Technol. (2008) 15(s1): 520-524

DOI: 10.1007/s11771-008-413-0

Viscous-flow properties and viscosity-average molecular mass of orange peel pectin

ZHOU Jin-hua(周尽花), WU Yu-xiong(吴宇雄), SHEN Zhi-qiang(沈志强)

(Science School, Central South University of Forestry and Technology, Changsha 410004, China)

Abstract: The viscous-flow properties of pectin from the residue of orange peel after extraction of essential oil and flavonoid were studied and the viscosity-average molecular mass (M_{v, ave}) of this kind of pectin was determined. Experimental results show that Arrhenius viscous-flow equation can be applied to describing the effect of temperature on viscosity of this kind of orange peel pectin solutions with the average viscous-flow activation energy being 17.91 kJ/mol (depending on the concentration). Neither power equation, 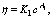 nor exponential equation, η=K₂exp(A₂c) can describe the effect of concentration on viscosity of this kind of orange peel pectin solutions well. However, it seems that exponential equation model is more suitable to describe their relation due to its higher linear correlation coefficient. Schulz-Blaschke equation can be used to calculate the intrinsic viscosity of this kind of orange peel pectin. The M_{v, ave} of the orange peel pectin is 1.65×10⁵ g/mol.

Key words: pectin; viscous-flow properties; viscosity-average molecular mass; orange peel

1 Introduction

Pectins are commonly used as gelling agents in desserts, yoghurts, confectioneries and jams. Commercial pectin preparations are divided into high- methoxyl(HM) and low-methoxyl(LM) pectins according to the degree of esterification(DE). Pectins with DE less than 50% are considered to be LM pectins^[1]. It is the hydrocolloid character of pectin that makes it such an important and versatile additive in food systems.

Viscous-flow properties are very important during the production and applications of pectin. Viscosity is a measure of molecular mass, and the higher the molecular mass is, the higher the viscosity is. Viscosity depends not only on the molecular mass but also on concentration and temperature^[2].

Citrus peels, including shaddock, orange, lemon and lime as well as apple pomace and sugar beet pulp, represent substantial sources of pectins^[3]. China is abundant in citrus fruits, especially the orange. However, the majority of orange is only processed to extract juice while the orange peel is discarded. It is not only wasting resources but also polluting the environment. To solve this problem and thus to improve the economic value of orange, essential oil has been extracted from orange peel, and then, flavonoid has been extracted from the residue, at last, pectin has been extracted.

The objectives of the present study were to determine the viscosity-average molecular mass and to study the viscous-flow properties of orange peel pectin extracted from the residue of orange peel after extraction of essential oil and flavonoid.

2 Experimental

2.1 Apparatus and materials

Orange peel pectin was extracted from the residue of orange peel after extraction of essential oil and flavonoid. 0.1 mol/L sodium phosphate buffer (pH value 7.0) and distilled water were used.

Main equipment and apparatus included Ubbelohde capillary viscometer, EM-WT501 stopwatch, ExpLorer OHAUS electric balance, PHS-3C acidometer, glass thermostated water bath and pycnometer.

2.2 Viscosity measurement

Orange peel pectin solution with certain concentration was prepared by dissolving the pectin in 0.1 mol/L sodium phosphate buffer. Then, distilled water, solvent sodium phosphate buffer and pectin solution were pipetted into the Ubbelohde capillary viscometer for viscosity measurements, respectively. The intrinsic viscosity of pectin was measured by dilution method^[4].

The viscosities of each fluid were determined at 20, 25, 30, 35, 40 and 45 ℃, respectively. Densities of all kinds of fluids were measured by means of pycnometer also at above-mentioned temperatures.

The absolute viscosities of solvent and orange peel pectin solutions were calculated on the basis of Poiseuille equation^[5] and the standard value of densities and viscosities of distilled water at above-mentioned different temperatures.

Poiseuille equation:

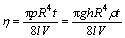                         (1)

where  η is the absolute viscosity of the measured solution; p is the difference in external pressure between the ends of the capillary tube; R and l are the radius and length of the tube, respectively; t is flowing time; h is the average height of the fluid during measurement; g is the acceleration due to gravity; ρ is the density; V is the volume of fluid that flows through the tube. If viscosities were measured by the same Ubbelohde capillary viscometer and at the same temperature, πghR⁴/(8lV) would be constant. Let it be A, then Eqn.(1) will be changed into

η=Aρt                                      (2)

The following equations can be achieved:

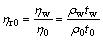                            (3)

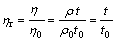                          (4)

where  η_w, η₀, η and ρ_w, ρ₀, ρ and t_w, t₀, t are viscosities, densities and flowing times of distilled water, solvent and pectin solutions, respectively; η_r0 and η_r are the relative viscosities of solvent and pectin solutions, respectively.

In Eqn.(4), because pectin solutions are very dilute, it is supposed that ρ₀≈ρ, and they can be cancelled. From the equation, viscosities of pectin solutions with different concentrations can also be calculated.

It is appropriate, then, to define the specific viscosity, η_sp as the fractional increase in viscosity caused by the presence of the dissolved pectin in the solvent^[6], as shown in Eqn.(5):

η_sp=η_r-1                                    (5)

η_sp and η_r clearly depend on the concentration of the pectin in solutions. However, the intrinsic viscosity^[4],  [η], defined as the limit of η_sp/c or ln η_r/c as the concentration approaches zero, is independent on the concentration of the solutions and is given by

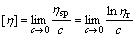                       (6)

2.3 Determination of viscosity-average molecular mass

Intrinsic viscosity is one of the characteristic values of molecules. When the sample, measuring conditions (solvent and temperature) are set, intrinsic viscosity only depends on the molecular mass of the measured sample. The relationship between intrinsic viscosity and molecular mass is described by Mark-Houwink-Sakurada equation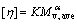^[7]:

                                (7)

where  K and α are constants and they depend on the nature of the sample and solvent, and on measuring temperature; M_v,ave is the viscosity-average molecular mass. At room temperature (25 ℃)，for pectin, K and α are 1.4×10^-6 and 1.34^[8], respectively.

3 Results and discussion

3.1 Effect of temperature on viscosity

The relationship between temperature and viscosity of orange peel pectin solutions with different concentrations is shown in Fig.1. Viscosity decreases as the temperature increases. The dropping of viscosity is due to the increasing of intermolecular distances which increase with the thermal energy of the molecules increasing when the pectin solutions are heated. At the same time, the viscosity also goes up with the rise of pectin concentration. Temperature has stronger effect on viscosity with higher pectin concentration.

3.2 Calculation of viscous-flow activation energy

The effect of temperature on viscosity of pectin

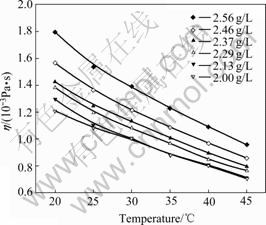
Fig.1 Relationship between temperature and viscosity of orange peel pectin solutions at different concentrations

solutions can be expressed by Arrhenius equation^[9]:

η=η₀exp[E_a/(RT)]                             (8)

where  η is the viscosity of pectin solutions (Pa?s); η₀ is the pre-exponential factor (Pa?s); E_a is the viscous-flow activation energy. The natural logarithm formation of Eqn.(8) is:

ln η=ln η₀+E_a/(RT)                            (9)

Since a plot of ln η versus (1/T) is linear, E_a and η₀ can be obtained easily from the slope and intercept, respectively. The values of E_a and η₀ calculated from Fig.2 are placed in Table 1.

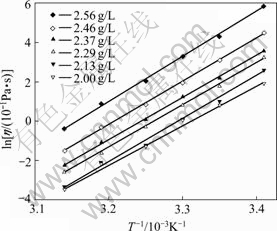
Fig.2 Calculation of viscous-flow activation at different concentrations

Table 1 E_a and η₀ of Arrhenius equation for pectin solutions with different concentrations

As seen in Table 1, apparently, E_a and η₀ vary with concentrations. However, E_a only changes a little within the measured concentration range. Thus, the average viscous-flow energy of 17.91 kJ/mol can be achieved.

3.3 Effect of concentration on viscosity

Changes of viscosity of pectin solutions with concentrations at different temperatures were shown in Fig.3.

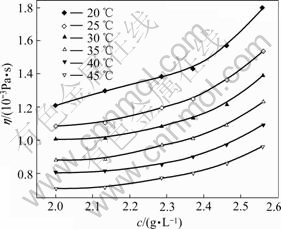
Fig.3 Effect of concentration on viscosity of orange peel pectin solutions at different temperatures

Variation of viscosity of pectin solutions with concentration may be described by the following equations^[10].

Power equation:

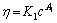                                  (10)

or exponential equation:

η=K₂exp(A₂c)                               (11)

where  K₁, K₂, A₁ and A₂ are constants and c is the concentration of pectin solution, g/L.

Eqns.(10) and (11) can be changed into natural logarithm formations:

ln η=ln K₁+A₁ln c                             (12)

ln η=ln K₂+A₂c                             (13)

Plots of Eqns.(12) and (13) are linear lines. A₁ and K₁ can be obtained from the plot of ln η versus ln c (Eqn.(12)), while A₂ and K₂ can be gained from the plot of ln η versus c (Eqn.(13)).

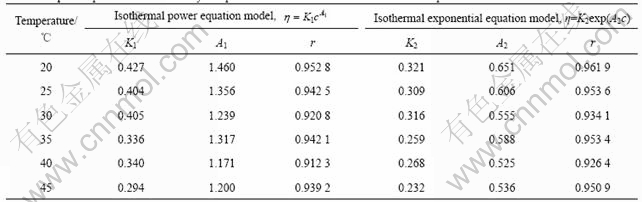
The experimental data of viscosity—concentration of orange peel pectin solutions were fitted to Eqns.(12) and (13) and the parameters together with the linear correlation coefficients r(s) are listed in Table 2.

Apparently, from the value of r, either power equation model or exponential equation model cannot describe the relationship between concentration and viscosity of orange peel pectin solutions well. However, it seems that exponential equation model is more suitable to be used to describe their relation due to its higher r. The experimental results show that concentration and temperature have strong effects on viscosity of orange peel pectin solutions. To some extent, the model will be useful to predict the change tendency of viscosity—concentration—temperature relation of pectin solutions from the residue of orange peel after extraction of essential oil and flavonoid.

Table 2 Equation parameters of viscosity and pectin concentration relation at different temperatures

3.4 Intrinsic viscosity and viscosity-average molecular mass

According to Eqn.(7), M_v,ave can be easily calculated from intrinsic viscosity [η], K and α. The following equations may be used to obtain [η].

Schulz-Blaschke equation^[4]:

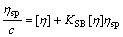                        (14)

Huggins equation^[11]:

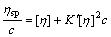                          (15)

Kraemer equation^[9]:

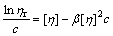                         (16)

and Martin equation^[12]:

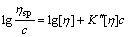                      (17)

The experimental data of η_sp/c—η_sp, η_sp/c—c, lnη_r/c—c, and lg(η_sp/c)—c of pectin solutions were fitted to Eqns.(14), (15), (16) and (17) respectively to investigate the linear relation between two variables. Linear lines could not be achieved for Eqns.(15), (16) and (17). It shows that Huggins equation, Kraemer equation and Martin equation are not suitable to be applied to calculate [η] of pectin from the residue of orange peel after extraction of essential oil and flavonoid. However, the plot of η_sp/c versus c (Eqn.(14)) is a good linear line (shown in Fig.4) with r being 0.999 9. Therefore, it is easy to draw the conclusion that Schulz-Blaschke equation can be used to gain [η] of this kind of orange peel pectin. The value of [η], which can be easily gained from the intercept of Fig.4, is 13.75 mL/g.

M_{v, ave} is calculated to be 1.65×10⁵ by introducing

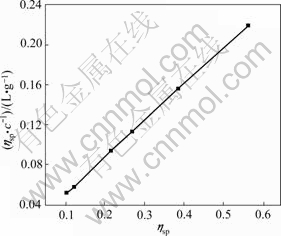
Fig.4 Plot of η_sp/c versus η_sp

[η]=13.75 mL/g, K=1.4×10^-6 and α=1.34 into Eqn.(7). That is, the viscosity-average molecular mass of pectin from the residue of orange peel after extraction of essential oil and flavonoid is 1.65×10⁵ g/mol.

4 Conclusions

1) Arrhenius viscous-flow equation is suitable to describe the effect of temperature on viscosity of pectin from the residue of orange peel after extraction of essential oil and flavonoid. The average viscous-flow activation energy of this kind of pectin is 17.91 kJ/mol (depending on the concentration of pectin solutions).

2) Neither power equation, 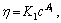 nor exponential equation, η=K₂exp(A₂c) can describe the effect of concentration on viscosity of pectin from the residue of orange peel after extraction of essential oil and flavonoid well. In comparison, exponential equation model is more suitable to describe their relation due to its higher linear correlation coefficient.

3) Schulz-Blaschke equation is suitable to calculate the intrinsic viscosity of pectin from the residue of orange peel after extraction of essential oil and flavonoid. The viscosity-average molecular mass of this kind of orange peel pectin is 1.65×10⁵ g/mol.

References

[1] KUUVA T, LANTTO R, REINIKAINEN T, BUCHERT J, AUTIO K. Rheological properties of laccase-induced sugar beet pectin gels [J]. Food Hydrocolloids, 2003, 17: 679-684.

[2] KAR F, ARSLAN N. Effect of temperature and concentration on viscosity of orange peel pectin solution and intrinsic viscosity-molecular weight relationship [J]. Carbohydrate Polymers, 1999, 40: 277-284.

[3] ARSLAN N, KAR F. Filtration of sugar-beet pulp pectin extract and flow properties of pectin solutions [J]. Journal of Food Engineering, 1998, 36: 113-122.

[4] HE Man-jun, CHEN Wei-xiao, DONG Xi-xia. Polymer physics (Revised version) [M]. Shanghai: Fudan University Press, 1990: 175-178. (in Chinese)

[5] ALLCOCK H R, LAMPE F W, MARK J E. Contemporary polymer chemistry (Copy) [M]. Beijing: Science Press, 2004: 453.

[6] CHEN T S, JOSLYN M A. The effect of sugars on viscosity of pectin solutions (II): Comparison of dextrose, maltose, and dextrins [J]. Journal of Colloid and Interface Science, 1967, 25: 346-352.

[7] ISIHARA A. On the viscosity of chain polymers [J]. Polymer, 1992, 33(1): 111-112.

[8] OWCS H S. Shape and size of pectinic acid deduced from viscometric measurements [J]. Journal of American Chemical Society, 1946, 68: 1628-1632.

[9] TANGLERTPAIBUL T, RAO M A. Intrinsic viscosity of tomato serum as affected by methods of determination and methods of processing concentrates [J]. Journal of Food Science, 1987, 52: 1642-1645.

[10] IBARZ A, PAGAN J, MIGUELSANZ R. Rheology of clarified fruit juices. (II): Blackcurrant juices [J]. Journal of Food Engineering, 1992, 15: 63-73.

[11] TEHCHIEN D C, KOKINI J L. Rheological properties and conformation of tomato paste pectins, citrus and apple pectins [J]. Journal of Food Science, 1987, 52(6): 1658-1664.

[12] MCMILLAN D E. A comparison of five methods for obtaining the intrinsic viscosity of bovine serum albumin [J]. Biopolymers, 1974, 13: 1367-1372.

(Edited by YANG Bing)

Foundation item: Project(104-0071) supported by Foundation of Talents of Central South University of Forestry and Technology, China

Received date: 2008-06-25; Accepted date: 2008-08-05

Corresponding author: ZHOU Jin-hua, PhD; Tel: +86-731-5623310; E-mail: zhoujinhua98@yahoo.com.cn