人工免疫网络算法的改进及免疫优化应用
郭鹏飞1, 2,王 嘉3,赵云丰1
(1. 北京科技大学 信息工程学院, 北京 100083;
2. 辽宁工程技术大学 软件学院,辽宁 葫芦岛,125000;
3. 煤炭科学研究总院 经济与信息研究所,北京 100013)
摘 要:基于人工免疫网络算法(aiNet)模型,借鉴禁忌搜索算法(TS)的思想,提出一种禁忌搜索与人工免疫的混合算法,即人工免疫网络算法(TS-aiNet)。在算法中引入禁忌表,禁忌那些在网络迭代中亲和度连续不再增加的细胞,并通过特赦准则赦免一些被禁忌的优良状态;增加1个记忆表,用于保存成熟的记忆细胞;重新定义高斯变异方式,以保证多样化的有效搜索。利用Markov链证明算法全局收敛性,通过对多个典型系统测试函数的仿真实验定量分析该算法的性能,并与经典克隆选择算法和opt-aiNet算法进行比较研究,分析特征参数对算法性能的影响。实验结果表明,该算法在多模态搜索空间中具有更强的全局收敛性、稳定性和寻找极值点能力,能够克服早熟现象,是一种有效的全局优化搜索方法。
关键词:人工免疫;优化;免疫网络算法;禁忌搜索算法
中图分类号:TP18 文献标识码:A 文章编号:1672-7207(2009)05-1345-09
Improved artificial immune network algorithm and
its application of immune optimization
GUO Peng-fei1, 2, WANG Jia3, ZHAO Yun-feng1
(1. School of Information Engineering, University of Science and Technology Beijing, Beijing 100083, China;
2. Software College, LiaoNing Technical University, Huludao 125000, China;
3. Institute of Economy and Information, China Coal Research Institute, Beijing 100013, China)
Abstract: A hybrid approach, tabu search artificial immune algorithm (TS-aiNet) was proposed based on aiNet model inspired by mechanism of tabu search algorithm. A tabu list was introduced to taboo such cell whose affinities didn’t continuously increase any more in the network. In some phrases the tabooed excellent cells were released according to aspiration criteria. To save mature memory cells, a memory table was added to cells network. In addition, the expression of Gauss mutation was redefined for diversity search in the process of global optimization. Markov chain was applied to prove global convergence. Performance analysis of optimization was carried out based on random simulation of some typical systems, which was compared with that of KLONALG and opt-aiNet algorithms. Finally, the influence of feature parameters on TS-aiNet algorithm was analyzed. The simulation results show that the presented approach has preferable global convergent ability and stability in multi-modal search space, and can avoid prematurity effectively. So it is demonstrated as a global optimized algorithm with feasibility and high efficiency.
Key words: artificial immune; optimization; artificial immune network algorithm; tabu search algorithm
复杂函数的优化问题,其特点是目标函数的局部最优解数量多,全局最优解难以确定。采用传统的数值优化方法难以求得所有的局部最优解,鉴于仿生进化特性在复杂优化问题求解方面具有的优势[1-2],基于进化的优化算法在函数优化取得较好的效果。人工免疫系统是一个动态进化系统,具有自然寻优的特性,优化是其一个重要的应用领域。人工免疫的算法和模型,在调度[3]、计算智能[4]、故障诊断[5]、优化学习、模式识别[6]等领域中取得了很好的效果,免疫算法所具备的特性、强大而丰富的信息处理能力,决定了其对优化问题的求解具有巨大的潜力。从人工免疫观点看,函数优化问题等同于抗体群体进化识别抗原的过程。抗原对应求解的问题,抗体对应问题的解,优化问题的最优解亲和度对应解的评估。Zheng等[7]研究了免疫遗传优化算法,较好地实现了函数优化问题;黄弦超等[8]在遗传禁忌算法基础上,采用免疫禁忌混合智能算法求解配电网检修计划的优化模型,属于组合优化问题,在解决电网检修规划问题中取得了较好的效果;汪嘉杨等[9]利用免疫禁忌优化算法对流域生态环境质量评价指数公式的参数进行优化,在生态环境评价中获得了较好的效果,其核心是禁忌搜索算法的应用。由于某些算法和模型的研究还处于起步阶段,存在如缺乏统一的免疫算法范式、仿生机理借鉴不够深入、算法的收敛性以及算法的执行效率有待提高等不足,本文作者对人工免役网络算法进行改进。
1 人工免疫网络算法与禁忌搜索算法
1.1 人工免疫网络算法
人工免疫网络算法(aiNet)[10]是在人工免疫系统基础上发展起来的一种智能算法,是由一些以一定连接强度联系起来的抗体群组成的网络,主要基于克隆选择、高频变异及免疫网络等免疫学原理实现。aiNet将要分析的数据看作抗原,将算法产生反映抗原特征的数据看作抗体,模拟免疫网络抗体抗原之间的相互刺激和作用,按照一定的算法实现数据处理。aiNet最初用来解决数据聚类问题,de Castro等[11]将聚类问题视为一种多峰优化问题,提出了一种面向多峰值函数优化的人工免疫网络,形成opt-aiNet算法。该算法能有效提取目标函数的绝大部分局部峰值,并具备群体数量自动调节和实数编码等优良特性。
由于自然进化和生命现象的“测不准”性,进化类算法不可避免地存在概率算法的缺陷,即存在未成熟收敛、种群多样性减少等“退化”现象。因而,aiNet在处理复杂、多模态、多峰值函数优化问题时,仍存在着如下问题:
a. 出现早熟现象,即在目标函数极值点过多和过于密集的情况下,有可能使算法过早收敛而搜索不到全部的极值点。
b. 迂回搜索,aiNet算法在增加随机生成细胞时,未考虑当前网络存在的细胞,盲目地增加随机生成的细胞和没有指导的迭代搜索,往往导致迂回搜索,不但增加了计算量,而且使算法过早收敛而搜索不到全部的极值点。
为了克服aiNet算法的不足,本文作者借鉴禁忌搜索的思想来改进aiNet算法。
1.2 禁忌搜索算法
禁忌搜索算法(Tabu search algorithm, TS)是一种全局逐步寻优、高效启发式优化理论。已被应用于调度、工作流程排序、旅行商和路由选择等问题[12],近年来,在函数优化方面得到较大的发展,其中,邻域函数、禁忌表、候选解、特赦准则等概念构成了禁忌搜索的关键。
由于TS算法具有灵活的记忆功能和特赦准则,在搜索过程中可以接受劣解,所以,具有较强的爬山能力,搜索时能够跳出局部最优解,转向解空间的其他区域,从而增加获得更好全局解的概率,因而,它是一种局部搜索能力很强的全局迭代寻优算法,可以很好地改善人工免疫网络算法早熟的问题。其不足之处是,迭代搜索过程是串行的,仅是单一状态的移动,非并行搜索,从而制约了收敛速度。而人工免疫网络算法的种群操作,保留了算法多出发点的优势,弥补了禁忌搜索缺乏并行性的弱点,因而,二者具有很好的结合空间。
2 禁忌人工免疫网络算法
2.1 改进策略
结合aiNet算法和TS算法各自的特点,提出了一种禁忌人工免疫网络算法(Tabu Search Artificial Immune Network, TS-aiNet)。
2.1.1 在人工免疫网络中引入禁忌搜索思想
引入一个灵活的存储结构和相应的禁忌准则,以避免迂回搜索,并通过特赦准则赦免一些被禁忌的优良状态。在TS-aiNet算法中,禁忌表用于记忆最近的一些迭代过程中亲和力没有增加的网络细胞,并将这些细胞禁忌。随机生成细胞时,在禁忌表的细胞形成的邻域中,将不被引入网络。当禁忌表中的细胞禁忌次数超过一定阈值时,将这些细胞特赦。特赦是为了进一步扩大搜索范围,使得一些优良对象重新参与免疫循环,保证了其对抗原空间的持续搜索能力和多样化的有效搜索,实现全局优化。这样,使得引入网络的随机生成的细胞有更好的分布性,减少迂回搜索,能够搜索到更多的极值点,同时提高搜索全局最优点的速度,从而提高TS-aiNet算法的全局搜索能力,加快收敛速度。
2.1.2 网络中增加免疫记忆
免疫细胞经历骨髓模型,成熟并进入免疫循环。成熟的免疫细胞具有固定的生命周期T。若在周期T内遇到抗原未能积累足够的亲和力变成记忆细胞,则走向死亡并被新生的免疫细胞代替,进行新的循环。若免疫细胞在其生命周期内积累了足够的亲和力,则成为记忆细胞。TS-aiNet算法模拟了这个机制,当网络中的细胞逐步成熟,并进入禁忌表,禁忌一段时间以后,该细胞将被释放,可以认为该细胞成了记忆细胞。细胞经历免疫成熟过程后,具备了免疫记忆功能,可以达到免疫记忆的目的。为了保护记忆细胞,增加了1个记忆表。记忆细胞会不断地被更新,每次进行网络抑制时,如果网络中存在一个细胞,它在某个记忆细胞的邻域内,并且它的亲和力比该记忆细胞的大,该记忆细胞将被其替换。这样使得记忆细胞逐渐趋近于局部极值,同时,通过更新替换,避免记忆表增长太大。
记忆细胞机制的引入,记忆表保存了搜索到的局部极值,使得这些局部极值对应的细胞不再参与细胞网络的迭代,从而使网络保持原有的规模,而不是逐渐增大,大大减少计算量。另外,当算法结束时,记忆表中的记忆细胞和即将进入记忆表的细胞就是所有的局部极值点,从中可以找到全局最优点。免疫记忆保存了各个局部最优解,这对于多峰值函数优化具有重要意义。
2.1.3 重新定义变异方式
在经典aiNet算法中,采用的变异方式为:

该方法的缺点是:
a. 由式(1)看出,该变异方式往往会使细胞的克隆体与父代细胞克隆体有一定重合;
b. 从式(2)看出,细胞的变异与细胞所对应的解所在的位置无关,而只与网络中其他细胞的亲和力有关,也就是说,在克隆选择过程中,评价的尺度仅仅是个体的亲和力。在当该细胞的亲和力在网络中越排在前面时,变异的范围就越小,这不完全合理。因为对于多峰值函数,每个峰值的函数值一般并不一定都能达到全局最大值,有的甚至比最大值小,若仅仅以亲和力作为评价指标,则很容易使种群中相似亲和力的个体迅速增加,而那些函数值较小峰对应的个体,很难进入下一代。因此,那些函数值较小的峰值很容易被漏掉,导致算法多样性差,容易出现未成熟收敛现象。
针对以上问题,利用迭代过程中细胞的变化来估计下一代的大致位置,然后,以这个位置为中心进行搜索,不仅依靠记忆细胞,而且也借助了网络结构。改进后,

通过这些改进,TS-aiNet算法可以具有更强的极值搜索能力,更快的收敛速度。
2.2 TS-aiNet算法的设计
2.2.1 TS-aiNet算法的设计
a. 基本思想。TS-aiNet算法中增加了禁忌表、记忆表和进化方向表。禁忌表存储网络迭代过程中亲和力不再增加的次数和达到设定阈值的细胞,记录细胞变量取值、亲和力和禁忌次数;记忆表存储记忆细胞、变量取值和亲和力;进化方向表存储细胞变异时的进化方向,它是一种串行结构的表,可以依据父代及当代个体在结构中的位置产生子代个体的进化方向,沿着亲和力上升的方向为目标进化方向。为加快寻求最优解的速度和精度,采用合理的进化方向很必要。
b. 个体评价。在TS-aiNet算法中,个体评价采用亲和度和浓度作为迭代群体的评价指标。亲和度用群体中2个个体之间的欧氏距离开方的倒数表示:

c. 抗体的初始化。在经典aiNet算法中,抗体所受到的刺激仅考虑了抗原对它的刺激,临近抗体对它的抑制推迟到了记忆细胞集产生后,删除细胞集里自识别的细胞来实现。因此,网络对于抑制阈值非常敏感。考虑到这个问题,在改进的算法中进行了初始克隆抑制,即在抗体初始化过程中引入了初始抑制。该抑制阈定义如下:
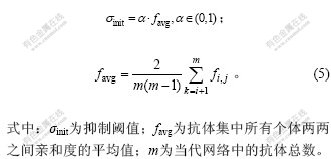
对于初始抗体集中的某一元素,计算它和其他各元素之间的相似度,将相似度小于阈值的元素删除,然后,补充与删除个体不相似的抗体到网络中。抗体的初始抑制一方面保证了网络中抗体多样性在一个较高水平,避免某种局部相似抗体大量存在;另一方面减小了网络抑制时对阈值的敏感性,决定了网络的特异性和可塑性。
d. 变异算子。为了保证群体多样性,采用改进后的变异方式(见式(3))。
e. 迭代停止条件。算法的迭代停止条件是达到禁忌表和记忆表中细胞的总数或者是达到最大迭代次数。
2.2.2 TS-aiNet算法的实现模型
禁忌人工免疫网络算法的实现模型如图1所示。算法结束时,利用禁忌表和记忆表中的细胞互相作用,通过阴性选择对亲和力小于抑制阈值的个体进行抑制,剩下的个体则保留起来。经过抑制后,若禁忌表和记忆表中的细胞总数比上一代的总数多,表示找到新的极值点。假如经过几次抑制,禁忌表和记忆表中的细胞总数不发生变化,则表明找不到新的极值点,停止搜索,禁忌表和记忆表中剩下的细胞和网络中最大亲和力细胞是问题的解[13]。

图1 禁忌人工免疫网路算法流程图
Fig.1 Flowchart of TS-aiNet algorithm
2.3 TS-aiNet算法的全局收敛性分析
由TS-aiNet算法的流程看,每一代计算从网络CN中的细胞开始,其分布反映了网络的基本状况,其他细胞群体实际上是细胞网络CN的一部分衍生体,由此可以通过研究不同代次免疫响应中细胞网络CN的变化来讨论算法的收敛性。
由于算法中不断采用较优的随机变异个体取代序列{CN (t)}中的对应个体,因此,该序列是一个随机过程。利用状态转移概率与极限理论对TS-aiNet算法进行收敛性分析,有如下定理。
定理1 在算法中,以免疫响应代数(迭代次数)t,t ? z+作为时刻坐标,{CN (t)}序列构成了一个有限状态的齐次Markov链。
证明 严格证明需要涉及许多概率和随机过程方面的论证,这里仅就定理进行分析。
每代网络细胞CN(t)由N个L-个体构成,每个细胞的取值是有限的,L-个体空间Ω所含个体的数目最多为2L个,N个L-个体所构成的种群组合不会超过2NL,因此,在t代细胞网络序列{CN (t)}的状态是有限的,所有的N个L-个体组合构成了序列{CN (t)}的状态空间,记为ΩN。(状态有限性)
每代CN (t)中的部分个体通过克隆扩增、高频变异、克隆选择和免疫补充过程进行更新,本代中的个体分布可以完全确定下一代个体的分布概率,而与本代之前的分布无关。(Markov性)
更新过程中,各种操作都与免疫进化的代数无关,故状态之间的转移只与构成状态的抗体个体有关,与免疫响应代数t无关。(齐次性)
因此,序列{CN (t)}构成了一个有限状态的齐次Markov链。证毕。
所以,其状态转移概率可以用状态转移矩阵来表示。若将细胞(状态)按亲和力从大到小进行排序,则改进算法的有限状态Markov链一步转移概率矩阵为:

于是可以定义算法的收敛性如下:
定义1 设Zt =max{ f(CN(t) (t)): t = 1, 2, …, N}是一个随机变量序列,该变量代表时间步t状态中网络中的最佳亲和力。若
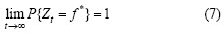
成立(其中,f * = max {f (b)| b ∈Ω},即全局最优值),则该算法以概率收敛到全局最佳解。
定理2[14] 设P为可归约随机矩阵,其中,Cm×n是一个基本随机矩阵,R和T不为0,则

是一个稳定的随机矩阵。
定理3 禁忌人工免疫网络算法以概率1收敛到全局最优解。
设Pij为从状态Ei到Ej的转移概率,从保留最优细胞(状态)的角度来考虑:
若f (Ej)>f (Ei),Pij则由正态分布的概率密度函数来确定;
若满足f (Ej)>f (Ei)的所有形成的空间Ej为C,则
若满足f (Ej)<f (Ei),则Pij = 0。
根据以上定理,所有包含在非全局最优状态中的概率收敛于0,而所有包含在全局最优状态中的概率收敛于1,因此,采用该算法所得解收敛于全局最优解。
上述分析表明,TS-aiNet算法是全局收敛的。另外,TS-aiNet算法不仅对初始网络的分布,而且对初始网络规模的影响有很好的免疫性,这无疑对保证算法的稳定具有重要意义。
3 仿真实验及分析
为了验证算法的性能,从局部收敛速度、收敛稳定性、搜索极值点的能力等方面进行定量分析[15],并就特征参数对算法性能的影响进行分析。
3.1 局部收敛速度比较分析
局部收敛速度指的是在搜索局部极值点时,找到局部极值点的速度。采用以下2个函数,并与CLONALG算法、opt-aiNet进行比较:

对于f1和f2 2个函数,3个算法运算结果如图2和3所示。

(a) 函数f1最大亲和力;(b) 函数f2最大亲和力
图2 最大亲和力变化过程图
Fig.2 Varying process of max affinity

(a) 函数f1收敛过程;(b) 函数f2收敛过程
图3 函数收敛过程路径平面显示
Fig.3 Convergent route of three functions in plane
采用3个算法运算的函数f1和f2的最大亲和力变化过程如图2所示。对于函数f1,由3种算法所得最大亲和力可以看出,TS-aiNet算法迭代31次就找到了极值点,CLONALG算法经过40次迭代,而opt-aiNet算法经过56次迭代;对于函数f2,TS-aiNet算法迭代29次就找到了极值点(1, 1),CLONALG算法经过100次迭代只收敛到原点(0, 0),没有找到(1, 1);opt-aiNet算法49次迭代找到极值点(1, 1)。所以,TS-aiNet算法搜索局部极值点时,局部收敛速度比其他2种算法的快。
图3所示为算法对2个函数收敛过程路径的平面显示,3种算法搜索起点都设为[-10,10]。从最大亲和力点坐标可以看出,TS-aiNet前进的距离是变化的,不是等距,而opt-aiNet前进的距离接近等距离,因为在TS-aiNet算法进行克隆变异过程中,利用了进化方向。同时,CLONALG算法前进的距离和方向是不规则的,因为CLONALG算法采用二进制编码,进行高频变异时,编码位置是随机的,在搜索局部极值点时不太稳定,有时可能会找不到局部极值点。
3.2 收敛稳定性比较分析
3.2.1 阶梯函数
阶梯函数是一种不连续函数,其不连续性质往往使一些算法收敛困难,其表达式为:
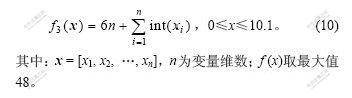
对于阶梯函数,3种算法的最终收敛结果如表1所示。
TS-aiNet算法在第26代就得到最优解,CLONALG算法需要42代,比较可知,收敛速度更快,局部搜索能力更强;opt-aiNet算法过早收敛,没有找到全局最优解。
表1 3种算法对阶梯函数的收敛结果
Table 1 Convergent results of algorithms for step function

3.2.2 Schaffer函数
Schaffer函数是一种只有1个全局最优点,且在全局最优点附近存在无穷个局部极值点将其包围的函数,Schaffer函数测试算法跳出局部极值点寻找全局最优点的能力,其表达式如下:

该函数在可行域内只有1个全局极大值点 f5(0, 0)=1,而其局部极大点为无穷多个。全局最优点周围有1个圈脊,因此,算法很容易停滞在此局部最优点。此函数形状相对于原点对称,且越接近最优点,函数值变化越剧烈,在最优点附近形成间隔很密、很陡的振荡峰。对于Schaffer函数,3种算法的收敛结果如表2所示。由表2可知,opt-aiNet算法陷入了局部极值点,没有找到全局最优点(0.000 1, 0.000 4),TS-aiNet算法在第59代时发现了最大极值点,比其他2种算法找到的最大极值点精确,且迭代次数最少。
表2 3种算法对Schaffer函数的收敛结果
Table 2 Convergent results of algorithms for Schaffer

以上测试结果表明,TS-aiNet算法对具有不同特点的优化问题具有较强的收敛能力,与另外2种算法相比,受函数不连续、非凸性和病态等因素的影响小,具有较强的全局最优解搜索能力。
3.3 搜索极值点能力比较分析
通常利用一些经典多峰函数测试算法搜索极值点的能力,根据搜索的结果种群分布情况评价算法性能。在此采用峰值比、搜索到的极值点的个数、亲和度函数的计算次数等指标进行定量评价。

在实验过程中,每个算法运算50次,取平均值,结果见表3。
峰值比反映算法找到的峰的质量,这一指标接越近1,表明算法性能越好。从表3可知,TS-aiNet算法的峰值比较其他2个算法的峰值更接近于1;TS-aiNet算法搜索到的极值点个数也较多,反映了其较强的全局搜索能力;亲和力函数的计算次数衡量算法的效率,TS-aiNet算法的计算次数较少,表明其计算的复杂度相对较小。
表3 3种算法对函数f 5的收敛结果
Table 3 Convergent results of algorithms for f5

由以上实验和统计结果可知,TS-aiNet算法具有多样性和优良的记忆功能,具有较强的稳定性、极值点搜索能力和较快的收敛速度等。
3.4 特征参数分析
TS-aiNet算法涉及的主要参数有网络规模N、抑制阈值、细胞最大克隆个数Nm、指数衰减率、禁忌阈值、特赦阈值和最大迭代次数。其中,禁忌阈值是某个细胞的亲和度连续不变的次数阈值,这个值越大,搜索到的极值点精度就越高,当该值过小时,容易导致不是极值点的细胞也会被加入禁忌表。禁忌阈值主要与细胞的矢量长度、细胞最大克隆个数有关,对算法的影响不是很大,因此,仅就与其对应的特赦阈值参数进行分析。
特赦阈值决定每个细胞被禁忌的次数,影响禁忌表的长度。当禁忌表长度变大时,补充到网络中的细胞分布性更好,有利于找到所有的极值点。取N = 40,Nm = 20,其他值固定,特赦阈值分别取6,8,10,12和14,并以Schubert函数为测试函数,TS-aiNet算法计算10次,得到收敛代数、亲和力计算次数、发现极值点个数和峰值比的最大值、最小值、平均值,结果见图4。

图4 特赦阈值对算法性能的影响
Fig.4 Influence of aspiration threshold on TS-aiNet
由图4可知,特赦阈值对收敛代数和亲和度计算次数影响不大,当该值从6增加到8时,搜索到极值点的个数和峰值比都增加,该值从8到12之间时峰值比都接近于1,当大于12时,发现极值点的个数和峰值比都减少。因而,综合考虑特赦阈值的取值为8~12较适合。
4 结 论
a. 禁忌人工免疫网络算法结合了人工免疫网络算法与禁忌搜索算法的优点,不仅包括抗体间促进和抑制的动态平衡,而且更好地反映了免疫系统的作用机制。仿真实验表明,与其他算法相比,该算法能更好地保持解的多样性,很好地避免了早熟问题,达到了全局寻优和快速收敛的目的,显示出更好的性能。
b. 禁忌人工免疫网络算法具备搜索多个最优点的能力,其相关结果还适用于图像配准。图像配准是寻找图像之间最佳转换参数的优化问题,由于其目标函数可能表现为非连续、多峰值和带噪声等各种形式,传统的搜索技术求解会遇到许多困难,而禁忌人工免疫网络算法可以很好地解决这种多模态的参数复杂寻优问题。人工免疫系统的分布式、并行和记忆性将会有助于图像配准快速处理算法的生成。如何提高算法的性能及算法在红外与可见光图像配准中的应用有待进一步研究。
参考文献:
[1] 李 婷, 赖旭芝, 吴 敏. 基于双种群粒子群优化新算法的最优潮流求解[J]. 中南大学学报: 自然科学版, 2007, 38(1): 133-137.
LI Ting, LAI Xu-zhi, WU Min. A novel two-swarm based particle swarm optimization algorithm for optimal power flow problem[J]. Journal of Central South University: Science and Technology, 2007, 38(1): 133-137.
[2] WANG Rong-ji, WANG Ling-ling, ZHAO Li-hua. Rapid prototyping process by neural network[J]. The Chinese Journal of Nonferrous Metals, 2005, 15(3): 452-457.
[3] Swiecicka A, Seredynski F, Zomaya A Y, et al. Multiprocessor scheduling and rescheduling with use of cellular automata and artificial immune system support[J]. IEEE Transactions on Parallel and Distributed Systems, 2006, 17(3): 253-262.
[4] De Castro L N, Timmis J. Artificial immune systems as a novel soft computing paradigm[J]. Soft Computing Journal, 2003, 7(7): 67-75.
[5] Gonzalez L, Cannady J. A self-adaptive negative selection approach for anomaly detection[C]//Proceedings of the Congress on Evolutionary Computation. Portland, 2004: 20-23.
[6] 焦李成, 杜海峰, 刘 芳, 等. 免疫优化计算、学习与识别[M]. 北京: 科学出版社, 2006: 218-235.
JIAO Li-cheng, DU Hai-feng, LIU Fang, et al. Immunological computation for optimization, learning and recognition[M]. Beijing: Science Press, 2006: 218-235.
[7] ZHENG De-ling, LIANG Rui-xin, FU Dong-mei, et al. Application of artificial immune system and artificial immune genetic algorithm to optimization[J]. Journal of University of Science and Technology Beijing, 2003, 3(25): 284-287.
[8] 黄弦超, 舒 隽, 张粒子, 等. 免疫禁忌混合智能优化算法在配电网检修优化中的应用[J]. 中国电机工程学报, 2004, 24(11): 96-100.
HUANG Xian-chao, SHU Juan, ZHANG Li-zi, et al. Distribution maintenance scheduling using an intelligent optimal approach mixed with immune algorithm and tubu search[J]. Journal of Chinese Electrical Engineering Science, 2004, 24(11): 96-100.
[9] 汪嘉杨, 李祚泳, 熊建秋, 等. 基于免疫禁忌优化算法的生态环境评价指数公式及其应用[J]. 生态与农村环境学报, 2006, 22(4): 25-29.
WANG Jia-yang, LI Zuo-yong, XIONG Jian-qiu, et al. Exponential formula for evaluation of eco-environmental quality based on immune taboo search[J]. Journal of Ecology and Rural Environment, 2006, 22(4): 25-29.
[10] de Castro L N, Zuben F J. aiNet: An artificial immune network for data analysis. Data mining: A Heuristic Approach. Hershey: Idea Publishing Group, 2001: 1-37.
[11] de Castro L N, Timmis J. An artificial immune network for multimodal function optimization[C]//Proceeding of IEEE Congress on Evolutionary Computation. Hawaii, 2002: 699-704.
[12] Tan P H, Rasmussen L K. Tabu search multi-user detection in CDMAEA[C]//Radio Vetenskapoch Kommunikation. Stockholm, 2002: 744-748.
[13] Jui Y W, Chung Y K. Artificial immune system for solving constrained global optimization problems[C]//The First IEEE Symposium on Artificial Life. Hawaii, 2007: 92-99.
[14] 叶尔骅, 张德平. 概率论与随机过程[M]. 北京: 科学出版社, 2005: 78-103.
YE Er-hua, ZHANG De-ping. Probability and stochastic process[M]. Beijing: Science Press, 2005: 78-103.
[15] SUN Rui-xiang, QU Liang-sheng. Quantitative evaluation of optimization efficiency for genetic algorithms[J]. Acta Automatica Sinica, 2000, 26(4): 552-556.
收稿日期:2008-12-09;修回日期:2009-03-10
基金项目:国家自然科学基金资助项目(60573016);北京市教委重点学科共建项目(XK100080537)
通信作者:郭鹏飞(1981-),男,辽宁朝阳人,博士研究生,讲师,从事软件工程与数据工程、智能算法研究;电话:13591990898;E-mail: intuguopf@163.com