DOI: 10.11817/j.issn.1672-7207.2016.10.039
相变蓄能抗冻太阳能平板集热器的设计与研究
赵静1,王智平1, 2,王克振1,2,陆鑫1,张楠1,寇宗丽1
(1. 兰州理工大学 材料科学与工程学院,甘肃 兰州,730050;
2. 兰州理工大学 能源与动力工程学院,甘肃 兰州,730050)
摘要:提出一种具有抗冻功能的相变蓄能太阳能平板集热器。该集热器在吸热板与保温层之间增加了一层相变潜热大、相变温度为277.15~281.15 K的相变蓄能材料。根据该集热器的传热机理,给出计算相变蓄能层设计厚度的公式。采用ANSYS Fluent软件建立该集热器的三维非稳态模型,模拟不同工况下集热器的出口温度及其内部水的最低温度。研究结果表明:在冬季环境温度最低日,相变蓄能抗冻集热器内水的最低温度高于275.15 K,能很好地起到抗冻作用;相变蓄能抗冻集热器与相同结构的普通集热器相比,冬季阴天和晴天代表日的净得热量分别高1.3 MJ/m2和0.7 MJ/m2。
关键词:相变蓄能层;抗冻;数值模拟;太阳能平板集热器
中图分类号:TK513; TK519 文献标志码:A 文章编号:1672-7207(2016)10-3575-07
The design and research of anti-freezing solar flat plate collector with phase change energy storage layer
ZHAO Jing1, WANG Zhiping1, 2, WANG Kezhen1, 2, LU Xin1, ZHANG Nan1, KOU Zongli1
(1. School of Material Science and Engineering, Lanzhou University of Technology, Lanzhou 730050, China;
2. School of Energy and Power Engineering, Lanzhou University of Technology, Lanzhou 730050, China)
Abstract: A new anti-freezing solar flat plate collector was designed, which added the energy storage layer of phase change between heat absorbing plate and thermal insulation layer. Phase change material had large latent heat, and phase transition temperature was 277.15-281.15 K. The formula to compute the designing thickness was derived based on its heat transfer mechanism. Three-dimensional unsteady numerical model of this collector was built by ANSYS Fluent. Using this model, outlet temperature and the lowest temperature of water in this collector were simulated under different working conditions. The results show that this new collector can effectively prevent the water in collector from freezing. The lowest temperature of water in this collector is higher than 275.15 K on the day of the lowest ambient temperature in winter. Compared with normal solar flat plate collector with the same construct parameters, the net heat gain of this new collector is 1.3 MJ/m2 higher on the typical cloudy day, and 0.7 MJ/m2 higher on the typical sunny day in winter.
Key words: phase change energy storage layer; anti-freezing; numerical simulation; solar flat plate collector
随着太阳能热利用的快速发展,太阳能集热器作为将太阳能集中转换为热能的部件,其传热过程分析[1-3]和结构优化设计[4-6]得到了广大研究者的重视。在低温工况下,平板集热器常因其内部传热工质水结冰膨胀而损坏。目前常用的防冻方法主要有用循环介质作传热工质的双回路系统、强制循环系统和排空系统[7]。这3种方法均是从集热器外部考虑,而魏一康等[8-10]则通过改变流道结构、材料解决集热器的抗冻问题。苏文佳等[11]在集热器吸热板与隔热层之间增加一层5 cm厚的无机相变储热材料(PCM03)。CHEN等[12]在集热器吸热板与隔热层之间增加一层石蜡储热材料,实现了集热储热一体化,避免了工质水的冻结,但其结构设计和相变材料的选取并不适合解决平板集热器的抗冻问题。为此,本文作者提出在吸热板与隔热层之间增加相变蓄能层的方式来解决集热器的抗冻问题。只要相变蓄能层厚度设计合理、选材合适,不仅能有效抗冻,而且有利于集热器的稳定运行。本文首先给出相变蓄能层厚度的设计原则,然后利用数值模拟的方法分析该集热器的抗冻效果和集热性能,并与普通平板集热器进行对比。
1 相变蓄能抗冻太阳能平板集热器的结构
相变蓄能抗冻太阳能平板集热器结构示意图如图1所示。与普通平板集热器相比,在其吸热板与保温层之间增加了相变蓄能层。该相变蓄能层选用低相变点、高相变潜热的材料。相变蓄能层的厚度应根据当地气象状况、集热器总热损系数及相变材料物性确定。当环境温度低于零摄氏度时,集热器内部持续向外散热,当温度降低到相变材料相变点时,该材料释放潜热,防止集热器内部水结冰,达到抗冻效果。
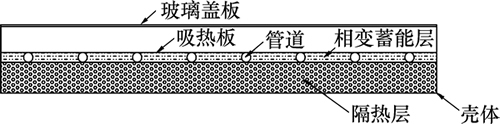
图1 相变蓄能层平板集热器结构简图
Fig. 1 Sketch map of solar flat plate collector with phase change energy storage layer
2 相变蓄能抗冻集热器模型的建立
2.1 模型假设
为计算方便,更好地建立模型,进行如下简化:1) 假设集热器结构为管-板式,且忽略联箱占据的面积;2) 集热器表面太阳辐射和环境温度均匀分布;3) 各支管内工质均匀流动;4) 忽略盖层及空气夹层的比热容;5) 忽略集热器边缘热损失;6) 忽略层与层之间的接触热阻;7) 物性参数在每相中不随温度变化。
根据假设可知,集热器内部各支管及其肋片的温度分布相同且关于中间截面对称,肋端绝热。简化后,物理模型如图2所示。该模型将集热器分为吸热板、水、相变蓄能层和隔热层4部分。表1所示为除相变蓄能层外其余各部分的几何及物性参数。各部分内部进行三维热传导,相互之间耦合传热。吸热板上表面一方面吸收一定太阳辐射量G,另一方面通过对流和辐射向外散失热量,热损失系数为ht,隔热层底部的热损失系数为hd。
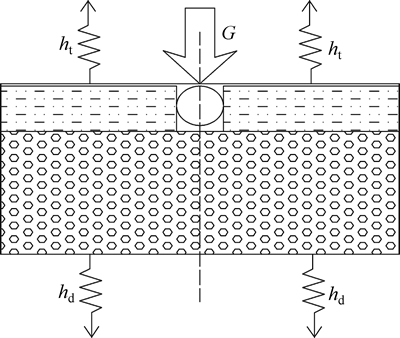
图2 相变蓄能抗冻集热器的物理模型
Fig. 2 Physical model of solar flat plate collector with phase change energy storage layer
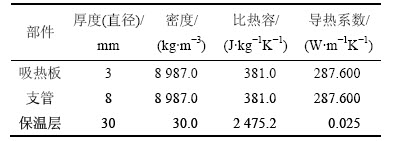
表1 集热器各部分的几何及物性参数
Table 1 Geometry and property parameter of solar flat plate collector
2.2 边界条件
2.2.1 热边界条件
根据图2所示模型,侧面和前后面的热流密度为0,可采用绝热边界条件;下表面与环境之间存在对流与辐射的热传递,可采用第3类热边界条件;而上表面首先吸收一定太阳辐射量,其次与环境之间发生对流与辐射形式的热传递,故需采用第3类和第2类2种边界条件。
集热器下表面有对流和辐射2种传热方式。由于辐射引起的热损失很低,忽略不计,故下表面的总传热系数hd为风吹过其表面时的对流换热系数hw,即
hd=hw=5.7+3.8v (1)
式中:v为风速。集热器顶部热损主要是环境与吸热板之间的对流和辐射引起的,相应地,上表面传热系数ht可以表达为
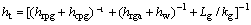 (2)
(2)
式中:hrpg和hcpg分别为吸热板与玻璃盖板之间的辐射换热系数和对流换热系数;hrga为玻璃盖板与天空之间的辐射换热系数;hw为玻璃盖板表面的对流换热系数;Lg和kg分别为玻璃盖板的厚度和传热系数。换热系数hrpg,hrga和hw可分别表示为:
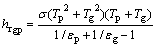
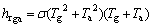
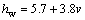
式中:σ为斯特凡-玻尔兹曼常数;Tp,Tg和Ta分别为吸热板温度、玻璃盖板温度、环境温度;εp和εg分别为吸热板和玻璃发射率。
对流换热系数hcpg通过努赛尔数Nu计算,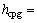
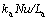 ,根据文献[13]可知Nu为
,根据文献[13]可知Nu为
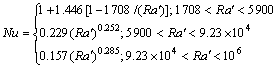
式中: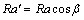 ;Ra为雷诺数;β为集热器倾角;ka为空气导热系数;La为空气夹层厚度。其中玻璃温度Tg采用文献[14]中方法估计。
;Ra为雷诺数;β为集热器倾角;ka为空气导热系数;La为空气夹层厚度。其中玻璃温度Tg采用文献[14]中方法估计。
集热器吸热板吸收的太阳辐射量Ga主要由斜面上接收的太阳直射辐射量Gb、散射辐射量Gd和玻璃盖板的透过率τ、吸热涂层的吸收率α决定,计算表达式为
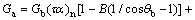
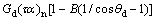 (3)
(3)
式中: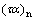 为太阳辐射垂直入射时集热器透射率与吸收率的乘积;B为集热器入射角修正系数的常数;θb和θd分别为直射和散射辐射的入射角。斜面上接收的太阳直射辐射量Gb、散射辐射量Gd以及入射角θb和θd的计算方法见文献[7]。
为太阳辐射垂直入射时集热器透射率与吸收率的乘积;B为集热器入射角修正系数的常数;θb和θd分别为直射和散射辐射的入射角。斜面上接收的太阳直射辐射量Gb、散射辐射量Gd以及入射角θb和θd的计算方法见文献[7]。
2.2.2 流动边界条件
在支管入口处,设置流速入口边界条件。集热与防冻都采用温度控制的方式。集热时,其出口与入口温差上限为5 K,下限为2 K,流速为0.06 m/s。需强迫循环防冻时,集热器出口处温度下限为275.15 K,上限为283.15 K,流速为0.02 m/s。
2.3 控制方程
利用流体软件ANSYS Fluent 建立三维非稳态模型,求解支管内工质的质量流量、平均出口温度及支管内工质的最低温度。流体的流动为非定常不可压缩黏性流体流动,工质的黏性为常数,则流体的流动应满足如下控制方程。
不可压缩非定常流体的连续性方程为
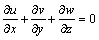 (4)
(4)
动量守恒方程为:
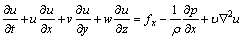
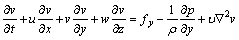 (5)
(5)
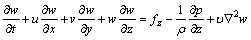
利用Fluent建立的模型求解平均出口温度及支管内工质的最低温度时,需要考虑集热器的传热过程。工质、吸热板和隔热层的传热为非定常无源过程,因此,相应的能量守恒方程为
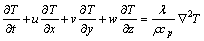 (6)
(6)
相变蓄能层在模拟过程中会发生熔化—凝固的变化,相应的能量微分方程如下(Fluent软件采用焓法模型对其进行求解)。
固相区:
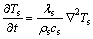 (7)
(7)
液相区:
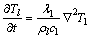 (8)
(8)
移动界面:
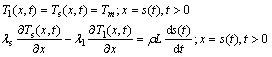 (9)
(9)
3 相变蓄能层厚度的设计
3.1 设计原理
相变蓄能层集热器抗冻时,吸热板和环境的温度变化如图3所示。设T0为太阳落山后集热器停止集热时吸热板的温度,Tt为抗冻最低温度,te-tb为抗冻时长。抗冻时长为每天无日照时间段内环境温度连续低于0 ℃的时长。在抗冻时长内,集热器的能量平衡方程为
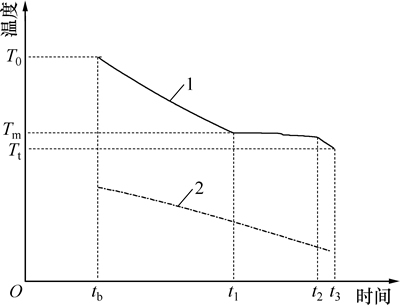
图3 抗冻时长内吸热板和环境温度随时间的变化
Fig. 3 Variation of ambient and heat absorbing plate temperature with time in length of antifreeze
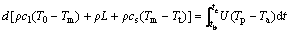
式中:d为相变蓄能材料的厚度;ρ,cl,cs和L分别为相变蓄能材料的密度、液态比热容、固态比热容、相变潜热;Tm为蓄能材料的相变温度;Tp为吸热板温度;Ta为环境温度;U为集热器总热损系数。若将吸热板温度变化分成3个时间段计算,并且假设每一时间段内的温度随时间呈线性变化,则在每一时间段内,集热器的能量平衡方程为
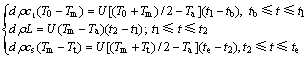 (10)
(10)
为计算简单,式(10)中每一时间段内的Ta都取抗冻时长内环境温度的平均值Ta0。则相变蓄能层的厚度为
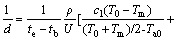
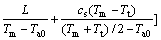 (11)
(11)
若根据上式确定相变蓄能材料的厚度,则需要根据当地气象条件确定设计抗冻时长te-tb、设计抗冻时长内环境温度平均值Ta0。采用统计方法确定设计抗冻时长,首先确定当地日最低气温低于0 ℃的时间N,称为可结冰日;其次统计可结冰日内每天环境温度低于0 ℃且无日照的时间m;最后确定设计抗冻时长te-tb,必须满足时间m小于te-tb的时间为K1N。K1为抗冻保证系数,可根据需要取0~1之间的常数,本文中取0.9。
同样采用统计的方法确定设计环境温度平均值Ta0。首先计算可结冰日内每天无日照时间内的环境温度平均值Ta;然后确定设计无日照时间内的温度平均值Ta0。Ta0的取值必须保证平均温度Ta大于Ta0的时间为K2N,K2为抗冻保证系数,可根据需要取0~1之间的常数,本文中取0.9。
3.2 相变蓄能层厚度
根据上述设计原理,计算兰州地区集热器总热损系数约为4.04 W/m2时,所需相变蓄能材料的设计厚度。相变蓄能材料选用十水硫酸钠的共晶盐化合物,表2所示为该材料的密度ρ、相变温度Tm、相变潜热L、液态比热容cl、固态比热容cs、液态导热系数λl、固态导热系数λs[15-16]。
经统计,兰州地区日最低气温低于0 ℃的可结冰日共143 d。图4所示为可结冰日的抗冻时长和无时间内的环境平均温度(其中,日序数指从当年1月1日起开始计算的时间,d)。从图4可见:当K1和K2取为0.9时,相应的设计抗冻时长和无日照时间内的环境平均温度分别为18 h和264.6 K;太阳落山后集热器停止集热时吸热板的温度T0取293.15 K,抗冻最低温度Tt取275.15 K。将各参数代入式(11),可得相变蓄能材料设计厚度为9.2 mm。
表2 相变蓄能材料的物性参数
Table 2 Property parameters of phase change material

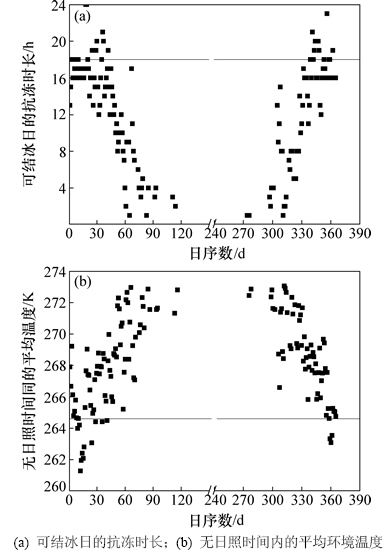
图4 兰州地区可结冰日的抗冻时长和无日照时间内的环境平均温度
Fig. 4 Length of antifreeze and average ambient temperature within non-sunshine time in freezing day in Lanzhou
4 模拟结果及分析
为全面考察相变蓄能层集热器的抗冻和集热性能,选取冬季阴天和晴天2种不同的工况,气象参数如图5所示。代表日分别为冬季晴天(2014-01-14)、阴天(2014-01-13),并且2014-01-13的环境温度为全年最低温。利用ANSYS Fluent软件,分别模拟相变蓄能层集热器与普通集热器(相同结构无相变蓄能层集热器)的出口温度、工质流量、冬季内部水的最低温度。普通集热器采用强迫循环的方式防冻,最低控制温度为275.15 K,上限为283.15 K,流速为0.02 m/s。代表日的模拟时段取当日10:00到次日10:00点,并且集热器始温度设为278.0 K。
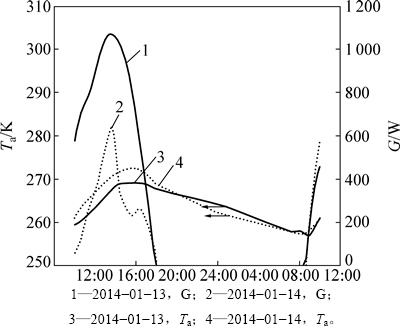
图5 代表日气象参数
Fig. 5 Meteorological parameters of typical day
2014-01-13(冬季阴天)模拟结果如图6所示,其中,图6(a)所示为集热器出口温度Tout和流量m,图6(b)所示为单位面积集热器的集热量θ和集热效率,图6(c)所示为集热器内水的瞬时最低温度Tmin。从图6可以看出:普通集热器响应速度快,白天集热量为2.9 MJ/m2,平均集热效率为27.4%;而晚上由于强迫循环造成的热损失为4.2 MJ/m2,则净得热量为-1.3 MJ/m2。相变蓄能层集热器响应较慢,白天出口温度缓慢升高,将吸收的热量储存在蓄能层中,但其最高温度也没有达到集热的上限温度,故水一直静止,集热量为0 MJ/m2;晚上,集热器将白天吸收的热量缓慢释放,集热器温度持续降低;当温度降低到278.15 K时,蓄能层发生相变,温度维持稳定,直到相变蓄能材料完全凝固后温度继续降低。从图6(c)可以看出:相变蓄能层集热器完全能达到抗冻的功能,8:40水的温度降到最低值276.04 K;当太阳升起时,温度开始升高;对于普通集热器,强迫循环同样可以达到抗冻的目的,但其热损失较大,而且泵的启停频繁。
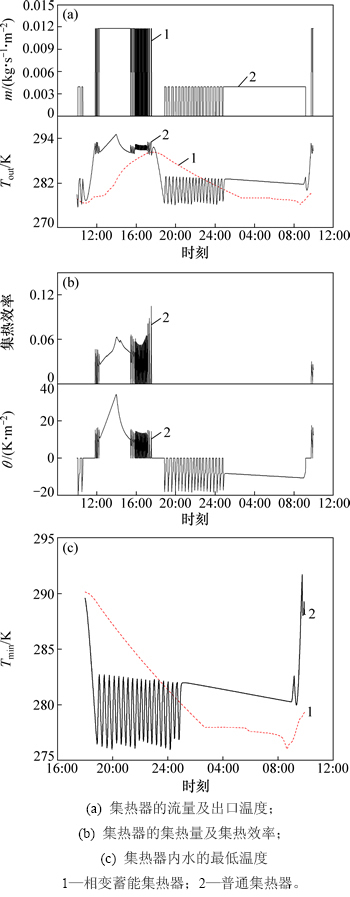
图6 冬季阴天代表日的模拟结果
Fig. 6 Simulation results on typical cloudy day in winter
2014-01-14(冬季晴天)模拟结果如图7所示,其中,图7(a)所示为集热器出口温度Tout和流量m,图7(b)所示为单位面积集热器集热量Q和集热效率,图7(c)所示为集热器内水的瞬时最低温度Tmin。从图7可以看出:对于普通集热器,响应速度快,从10:08开始集热,18:00结束,出口温度在13:51达到最高值302.04 K,同时集热功率也达到最大值684.35 W/m2;集热器效率先升高,然后进入稳定状态,最后在太阳快落山时,受集热器热容的影响造成效率急剧上升;与普通集热器相比,相变蓄能层集热器响应较慢,12:28开始集热,持续到19:18结束,出口温度在15:18达到最高值299.23 K,同时集热功率也达到最大值581.87 W/m2;集热器效率持续升高。白天普通集热器的日总集热量为13.1 MJ/m2,平均效率为56.6%,而晚上其因强迫循环造成的热损失为4.3 MJ/m2,则净得热量为8.8 MJ/m2,相应的效率为37.9%;与普通集热器相比,相变蓄能集热器用自身储存的热量抗冻,即白天的总集热量与其净得热量相等,为9.5 MJ/m2,平均集热效率为40.8%。从图7(c)可以看出:相变蓄能层集热器完全能达到抗冻的目的,水的最低温度达到276.23 K;强迫循环同样可以达到抗冻的目的。
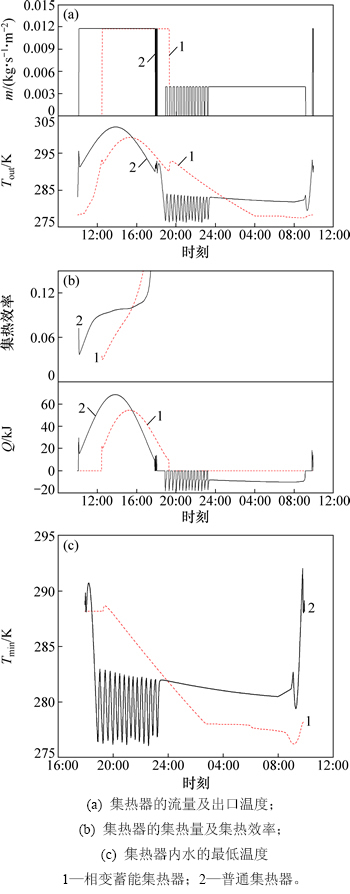
图7 冬季晴天代表日的模拟结果
Fig. 7 Simulation results on typical sunny day in winter
5 结论
1) 当K1和K2为0.9时,兰州地区的设计抗冻时长和无日照时间内的环境平均温度分别为18 h和264.6 K。根据文中提供的相变材料参数和集热器参数,所需相变蓄能层的厚度为9.2 mm。
2) 模拟结果显示在冬季环境温度最低日2014-01-13,支管内水的温度降到最低值276.04 K,相变蓄能层集热器能够达到抗冻的效果。
3) 冬季时,与普通集热器相比,相变蓄能层集热器的响应速度慢2.5 h,白天集热量少,但是净得热量高。2014-01-13和2014-01-14相变蓄能集热器的净得热量分别比普通集热器高1.3 MJ/m2和0.7 MJ/m2。
参考文献:
[1] RODR GUEZ-HIDALGO M C, RODR
GUEZ-HIDALGO M C, RODR GUEZ-AUMENTE P A, LECUONA A, et al. Flat plate thermal solar collector efficiency: transient behavior under working conditions.Part Ⅰ: model description and experimental validation[J]. Applied Thermal Engineering, 2011, 31(14/15): 2394-2404.
GUEZ-AUMENTE P A, LECUONA A, et al. Flat plate thermal solar collector efficiency: transient behavior under working conditions.Part Ⅰ: model description and experimental validation[J]. Applied Thermal Engineering, 2011, 31(14/15): 2394-2404.
[2] HOU Hongjuan, WANG Zhifen, WANG Ruzhu, et al. A new method for the measurement of solar collector time constant[J]. Renewable Energy, 2005, 30(6): 855-865.
[3] KONG Weiqiang, WANG Zhifeng, FAN Jianhua, et al. An improved dynamic test method for solar collectors[J]. Solar Energy, 2012, 86(6): 1838-1848.
[4] CADAFALCH J, CONSUL R. Detailed modeling of flat plate solar thermal collectors with honeycomb-like transparent insulation[J]. Solar Energy, 2014, 107(9): 202-209.
[5] DAMIR D, MLADEN A. Numerically assisted analysis of flat and corrugated plate solar collectors thermal performances[J]. Solar Energy, 2012, 86(9): 2416-2431.
[6] KESSENTINI H, CAPDEVILA R, CASTRO J, et al. Three dimensional heat transfer analysis of combined conduction and radiation in honeycomb transparent insulation[J]. Solar Energy, 2014, 105(7): 58-70.
[7] 何梓年. 太阳能热利用[M]. 合肥: 中国科技大学出版社, 2009: 18-200.
HE Zinian. Solar thermal utilization[M]. Hefei: University of Science and Technology of China Press, 2009: 18-200.
[8] 魏一康, 喜文华, 袁俊, 等. 平板太阳集热器结构抗冻思想与吸热板材料性能特征[C]//严陆光, 翟容强. 21世纪太阳能新技术: 2003年中国太阳能学会学术年会论文集. 上海: 上海交通大学出版社, 2003: 407-410.
WEI Yikang, XI Wenhua, YUAN Jun, et al. The antifreeze mechanism of flat plate-type solar collector and material characteristics of absorber plate[C]//YAN Luguang, ZHAI Rongqiang. The New Solar Energy Technology in the 21st Century: the Monograph of Academic Annual Conference. Shanghai: Shanghai Jiaotong University Press, 2003: 407-410.
[9] 陶桢, 葛洪川, 吕俊生. 抗冻太阳热水器冻结顺序的理论研究[J]. 太阳能学报, 1993, 14(1): 30-34.
TAO Zhen, GE Hongchuan, L Junsheng. Theoretical study on freezing time order control of solar collector[J]. Acta Energiae Solaris Sinica, 1993, 14(1): 30-34.
Junsheng. Theoretical study on freezing time order control of solar collector[J]. Acta Energiae Solaris Sinica, 1993, 14(1): 30-34.
[10] 陶桢. 抗冻太阳热水器[J]. 太阳能, 1998, 19(3): 21.
TAO Zhen. The antifreeze solar collector[J]. Solar Energy, 1998, 19(3): 21.
[11] 苏文佳, 左然, 张志强, 等. 太阳能平板集热/储热系统[J]. 太阳能学报, 2008, 29(4): 449-453.
SUN Wenjia, ZUO Ran, ZHANG Zhiqiang, et al. Flat-plate solar collector/storage system[J]. Acta Energiae Solaris Sinica, 2008, 29(4): 449-453.
[12] CHEN Zhenqian, GU Mingwei, ENG Donghua. Heat transfer performance analysis of a solar flat-plate collector with an integrated metal foam porous structure filled with paraffin[J]. Applied Thermal Enginnering, 2010, 30(14/15): 1967-1973.
[13] BUCHBERG H, CATTON I, EDWARDS D K. Natural convection in enclosed spaces: a review of application to solar energy collection[J]. Journal of Heat Transfer, 1976, 98(2): 182-188.
[14] AKHTAR N, MULLICK S C. Appromimate method for computation of glass cover temperature and top heat-loss coefficient of solar collectors with single glazing[J]. Solar Energy, 1999, 66(5): 349-354.
[15] 许建俊, 华泽钊. Na2SO4·10H2O溶液的特性及其在蓄冷空调技术中的应用[J]. 制冷学报, 1997(19): 1-6.
XU Jianjun, HUA Zezhao. The characteristics of Na2SO4·10H2O and its application in cool storage technology[J]. Journal of Refrigeration, 1997(19): 1-6.
[16] 谢全安, 郑丹星, 武向红. Na2SO4·10H2O共晶盐的热化学研究[J]. 太阳能学报, 2002, 23(1): 1-6.
XIE Quanan, ZHENG Danxing, WU Xianghong. Thermochemical study on eutectic composed by Na2SO4·10H2O[J]. Acta Energiae Solaris Sinica, 2002, 23(1): 1-6.
(编辑 陈灿华)
收稿日期:2015-10-12;修回日期:2015-12-25
基金项目(Foundation item):国家“十二五”科技支撑计划项目(2011BAJ03B08);甘肃省科技重大专项(1102GKDA049)(Project(2011BAJ03B08) supported by the National Key Technology R&D Program of China; Project(1102GKDA049) supported by the Science and Technology Department of Gansu Province)
通信作者:王智平,教授,从事太阳能低温热利用研究;E-mail: solar_energy8@126.com