Continuous electromagnetic separation of inclusion from
aluminum melt using alternating current
ZHANG Bang-wen(张邦文)1, REN Zhong-ming(任忠鸣)2, WU Jia-xiong(吴加雄)2
(1. State Key Laboratory of Plastic Forming Simulation and Die and Mould Technology,
Huazhong University of Science and Technology, Wuhan 430074, China;
2. Shanghai Enhanced Laboratory of Metallurgy, Shanghai University, Shanghai 200072, China)
Received 20 June 2005; accepted 19 September 2005
Abstract: A novel scheme about the continuous electromagnetic purification of aluminum melt was put forward based on the utilization of a square separation pipe and a 50 Hz alternating current to produce electromagnetic force. It is experimentally found that with electrical current of 400 A/cm2, it takes only 10 s to remove 95% inclusion from aluminum melt. Comprehensive numerical simulations were carried out to investigate the dynamics mechanisms behind the process. The results show that the removal of inclusion is attributed to the cooperative effects of electromagnetic buoyancy and the secondary flow induced by the rotational electromagnetic force, and the removal efficient increases with the size of inclusion and the electrical current imposed. Theoretical predictions on the distribution and removal efficiency of inclusion were supported by the experiments.
Key words: aluminum melt; alternating current; flow field; concentration field; inclusion; electromagnetic separation
1 Introduction
Due to the increasing demands for clear and high-performance aluminum product, it becomes an urgent task to further reduce the level of impurity especially the inclusion in aluminum melts[1－3]. Unlike conventional methods for inclusion removal such as refining and filtration, electromagnetic separation bears the advantages of higher efficiency and free-pollution, and has abstracted more and more attention from both academic and engineering circles. So far, theoretical[4－8] and experimental[ 2, 3, 9－13] studies have been made to focus on the following issues: how to elevate the removal efficiency, appropriate scheme to generate electromagnetic force and better hydraulics design of separation pipe etc, and have obtained successes to some extent. Of those schemes to generate electromagnetic force, the one in which a 50 Hz alternating current was utilized seems attractive because of its economy and simplicity[7, 12]. In previous work[12], we experimentally investigated the static electromagnetic separation for Al-22%Si(mass fraction, the same below if not mentioned) alloy based on this scheme. Following it, this study is devoted to the continuous electromagnetic purification of aluminum alloy (Al-8%Mg-0.7%Al2O3) by the combination of experiments with numerical simulations, and a square pipe is used as the separator of inclusion.
2 Theoretical analysis
2.1 Magnetic field
For a linear conducting medium in low- frequency range, Maxwell’s equation is reduced to the eddy current equation as
(1)
where J = (0, 0, J) is electrical current density, imposed in the axial direction of square pipe shown as Fig.1, μ0 is permeability of free space, σ is electric conductivity. And
(2)
where φ is scalar electric potential, A is vector magnetic potential, which defined as B=▽×A, B is magnetic current density.
For two-dimensional problem in X-Y plane with Z-direction imposed current J, the solution of Eqn.(1) can be expressed by[14]
(3)
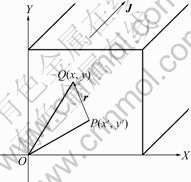
Fig.1 Calculated area of square pipe used for electromagnetic separation
where s denotes the circle of cross section surrounding the current, r is the distance from a source point P(x′, y′) to the field point Q(x, y) , as shown in Fig.1. In the case that sine current is applied, Eqn.(3) can be replaced by following complex form for convenience
(4)
The superscript “·” means complex number, and ω is anglular frequency.
The last item in the above equation is a constant and is determined by the continuity equation of electrical current
(5)
where 
is applied current intensity.
By changing Eqns.(4) and (5) into differential forms,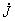 
can be solved numerically by elimination’s method. Then, the magnetic current density is calculated by
(6)
Finally, the time-average electromagnetic force is obtained by following components
(7)
2.2 Flow field
The force expressed in Eqn.(7) is rotational, as a result, a secondary flow will be induced in cross-section of separation pipe[5]. In the case of Re<2 300, the controlling equations of fluid flow are written as[8]
Continuity
(8)
x-momentum
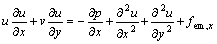(9)
y-momentum
(10)
where u and v stand for the velocity of fluid in x and y directions, respectively; and p is the pressure. The boundary conditions are given by
x=0, 0＜y＜b, 
x=a, 0＜y＜b, u=v=0
y=0, 0＜x＜a, 
y=b, 0＜x＜a, u=v=0
2.3 Concentration field and removal efficient
When the melt passes the separation pipe, a time-dependent concentration field will be experienced if one observer follows the fluid element. That is, at t=0, the inclusions are distributed randomly and uniformly in the inlet. With the advance of molten aluminum, they gradually migrate toward the walls driven by electromagnetic buoyancy so that the number of inclusion resided in separator gets less and less. At t=Tr when the melt arrives at the outlet of pipe, only least inclusions can be found in aluminum melt, where Tr ≈L/U presents the mean residence time of molten melt in the pipe, L is the length of separation pipe, U is the mean velocity of molten melt. In terms of this model, the inclusion distribution or concentration field can be expressed by
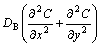(11)
and
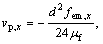
(12)
where C is the concentration of inclusion, vp,x, vp,y are the migration velocity of inclusion in x and y direction due to electromagnetic buoyancy, DB=kBT/(3πμfd) is Brownian diffusion coefficient of inclusion. The initial and boundary conditions are
t=0, 0＜x＜a, 0＜y＜b, C=1
x=0, 0＜y＜b, 
x=a, 0＜y＜b, nx=λvxC
y=0, 0＜x＜a, 
y=b, 0＜x＜a, ny=λvyC
where nx, ny present the fluxes of particle normal to the wall, λ is the adhesion efficiency of inclusion in wall, as defined in Ref.[15].
Numerically, The SIMPLE algorithm[15] was adopted to solve the flow field presented in Eqns.(8)－(10), followed by the concentration field of inclusion. The removal efficiency of inclusion at arbitrary moment, t, is determined from following equation
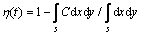(13)
As mentioned previously, when t=Tr, η presents the terminal removal efficiency of inclusion from molten aluminum by electromagnetic separation.
3 Experimental
As shown in Fig.2, experimental setup consists of furnace body, separation pipe and power-supply system. The furnace body is made of fire-resistant bricks inside and steel plates outside, having a cuboid shape (70 cm×30 cm×30 cm), on the sides of furnace, two pools are formed which are connected by the rectangular separation pipe. The pipe is 8 mm×8 mm in cross section and 30 cm in length. A 50 Hz alternating current ranging from 0 to 300 A is imposed on the graphite elec- trodes in the bottom of pools.
Fig.2 Sketch of continuous purification of aluminum melt using 50 Hz AC current
Al-8%Mg-0.7%Al2O3, prepared by co- melting and continual mixing in induction furnace, is used as experimental alloy. The addition of Mg aims to improve the wettability of aluminum melt to alumina inclusions, which are 30－75 μm in size.
Firstly, the furnace was preheated to 300－400 ℃, and the electrical power is turned on. Then molten alloy at 800 ℃ was poured into the pool in left side. When the melt passes through the separation pipe, the close circuit forms, indicating the starting of electromagnetic separation, purified melt gets off the outlet of furnace. After about 5 min, the unpurified samples were ex- tracted using a quartz-glass tube from random locations in left pool, while the purified ones from the point immediately near the outlet of separation pipe. The content of whole oxygen of sample is analyzed using a nitrogen/oxygen determinator (LECO TC-436). When the experiments finished, the solidified bars resided in the pipe were cut, giving the cross sections for polishing. The crystallographic structure of samples was observed and imaged with optical microscope (MVT). The measured removal efficiency of inclusion was evaluated from the following expression:
(14)
where [O]in and [O]out present the oxygen content of unpurified and purified samples, respectively.
4 Results and discussion
Fig.3 illustrates the calculated electromagnetic force field, flow field and concentration field of a 30 μm inclusion at t=3 s in the first quadrant of rectangular pipe imposed by a 250 A (391 A/cm2) alternating current. Fig.3(a) shows the time-average electromagnetic force points to the center of separation pipe, and descends in magnitude. The maximal force exists in the edge with a density of 2×104 N/mm3, which approximates to the gravity of molten aluminum. Because the electro- magnetic force is rotational, a complex secondary flow pattern with four symmetric axes is induced, as shown in Fig.3(b), which agrees with Taniguchi’s results[5] obtained by other method. Correspondingly, the maximal convection velocity produced is 6 mm/s. The mixing effect of vortex flow helps the transport of inclusion, especially those in the center, where the electromagnetic force electromagnetic buoyancy is rather small. It is just the cooperative effects of electromagnetic buoyancy and the secondary flow that results in the migration of inclusion the walls. As a result, an enrichment layer of inclusion is formed near the walls, as demonstrated in Fig.3(c), which not only exhibits a good symmetry due to the symmetry of force and flow fields, but also predicts that this is a best enrichment of inclusion in the four corners of square pipe.
Fig.4 presents the representative macrostructure of samples cut at z=10, 20 and 30 cm, where z is the distance from the inlet of pipe. In the experiment, the electrical current imposed I=200 A, the mean flow velocity v=2.8 cm/s. At z=10 cm, the inclusions have experienced an initial migration from the center to boundary of pipe, so a ring-like area filled by inclusions appears around the cross section, with bigger gray air hole existing at the same time. With the advance of molten melt, more and more inclusions reach the walls, results in a thin layer of enriched inclusions near the walls at z=20 cm, specially in the four corners as expected. Near the outlet of pipe (z=30 cm), the surface of sample appears rather smooth without any visible impurity, indicating that most of inclusion have been removed from the melt by electromagnetic separation.
Fig.3 Calculated electromagnetic force field(a), flow field(b) and concentration field of 30 μm inclusion at t=3 s(c) in separation pipe imposed by 250 A alternating current
Fig.4 Macrostructures of samples obtained from different cross-sections with distance z=10 cm (a), z=20 cm (b) and z=30 cm (c) from inlet of pipe
Fig.5 shows the calculated concentration distribu- tion for a 50 μm inclusion at different moments when I= 200 A and v=2.8 m/s. Here, t=3.8, 7.7 and 11.5 s corres- pond roughly to z=10, 20 and 30 cm in Fig.4. It can be seen that the concentration is about 0.5 at t=3.8 s, less than 0.3 at t=7.7 s, and only 0.04 at t=11.5 s when the melt leaves the pipe. The tendency of concentration evolution is consistent with that observed in the experiment, as shown in Fig 4.
Fig.5 Predicted evolution of concentration field of 50 μm inclusion with time: (a) t=3.8 s; (b) t=7.7 s; (c) t=11.5 s
Table 1 lists the whole oxygen before ([O]in) and after ([O]out) purification, and the inclusion removal efficiency (η) obtained from for two groups of typical samples in the case that I=250 A and Tr =12.3 s. It shows the oxygen content of contaminative aluminum is about 0.32%, and sharply decreases by 97% after purification. It is surprising that only 1.8×10－5 oxygen is detected in sample 4.
Fig.6 shows the removal efficiency of inclusion as a function of the residence time (Tr) of molten aluminum imposed by current of I=150 A (234 A/cm2) and I=250 A (391 A/cm2). Scattered black dots stand for the measured data, two solid lines for the calculated results of inclusion of 30 and 75 μm, respectively. It shows the lower the flow velocity is, the longer the residence time is, the more effective the removal of inclusion is. The dependence of η on Tr is nonlinear, i.e., η sharply ascends at lower Tr, and tends to 1.0 when Tr >15 s irrespective of the electrical current. Moreover, the removal efficiency of inclusion increases with rising size of inclusion and the electrical current imposed, because the increases in inclusion size and electrical current mean more electromagnetic buoyancy and migration velocity for the inclusions as expressed by see Eqn.(12). As shown in Fig.6(b), with an electrical current of about 400 A/cm2, it takes only 10 s to remove 95% of inclusion from molten aluminum. The calculated removal efficiency of inclusion agrees with that obtained in experiments.
Table 1 Oxygen content of unpurified ([O]in) and purified ([O]out) samples, and removal efficiency of inclusion at I=250 A and Tr =12.3 s
Fig.6 Dependence of purification efficiency of aluminum melt on residence time in separation pipe: (a) I=150 A; (b) I=250 A
5 Conclusions
1) The time-average electromagnetic force points to the center of separation pipe, and descends in magnitude. The electromagnetic force is rotational, so induces a complex secondary flow in the cross section of separation pipe, which accelerates the transport of inclusion. The removal of inclusion results from the cooperative effects of electromagnetic buoyancy and the secondary flow.
2) The removal efficiency of inclusion increases with rising size of inclusion and the electrical current imposed. With an electrical current of about 400 A/cm2, it takes only 10 s to remove 95% of inclusion from molten aluminum. Theoretical predictions on inclusion distribution and the removal efficient of inclusion were supported by the experiments.
References
[1] Crepeau P N. Molten aluminum contamination: gas, inclusions and dross [J]. Modern Casting, 1997, 87(7): 39－41.
[2] EL-Kaddah N , Patel A D , Natarajan T T. The electromagnetic filtration of molten aluminum using an induced current separator [J ]. JOM, 1995, 47(5): 46－49.
[3] LI Ke, WANG Jun, SHU Da, et al. Separation of inclusion from aluminum melt using alternating electromagnetic field [J]. Trans Nonferrous Met Soc China, 2002, 12(6): 1107－1111.
[4] Leenov D, Kolin A. Theory of Electromagnetophoresis(I): magnetohydrodynamic forces experienced by spherical and symmetrically oriented cylindrical particles [J]. J Chem Phys, 1954, 22(4): 683－688.
[5] Taniguchi S, Brimacombe J K. Application of pinch force to the separation of inclusion particles from liquid steel [J ] . ISIJ International, 1994, 34(9): 722－731.
[6] SHU D, SUN B D, WANG J, et al. Study of electromagnetic separation of nonmetallic inclusions from aluminum melt [J]. Metall and Mater Trans A, 1999, 30(11): 2979－2988.
[7] ZHANG Bang-wen, REN Zhong-ming, ZHONG Yun-bo, et al. Theoretical investigation on by-only-current electromagnetic separation of inclusion from molten melts [J ] . Acta Metall Sinica, 2002, 15(5): 416－424.
[8] ZHANG Bang-wen , REN Zhong-ming , DENG Kang, et al. Effects of direct current on the electromagnetic separation of inclusion from molten melts [J]. Comput Phys, 2002, 19(6): 527－531. (in Chinese)
[9] Park J, Morihira A, Sassa K, et al. Elimination of non-metallic inclusions using electromagnetic force [J]. Tetsu-to-Hagané, 1994, 80(5): 31－36.
[10] Yamao F, Sassa K, Iwai K, et al. Separation of inclusion in liquid metal using fixed alternating magnetic field [J]. Tetsu-to-Hagané, 1997, 83(1): 30－35.(in Japanese)
[11] ZHONG Yun-bo, REN Zhong-ming, DENG Kang, et al. Separation of inclusion from liquid metal contained in a triangle/square pipe by traveling magnetic field [J]. Trans Nonferrous Met Soc China, 2000, 10(2): 240－245.(in Chinese)
[12] WU Jia-xiong, REN Zhong-ming, ZHANG Bang-wen, et al. Electromagnetic purification of aluminum alloy melt only by alternating current [J]. The Chinese Journal of Nonferrous Metals, 2004, 14(3): 354－358. (in Chinese)
[13] LI Ke, NI Hong-jun, SHU Da, et al. Continuous cleaning of A356 alloy melt using high frequency electromagnetic field [J]. Trans Nonferrous Met Soc China, 2004, 14(1): 82－87.
[14] FAN Ming-wu, YAN Wei-li. Integral Equation Method on Electromagnetic Field [M]. Beijing: China Machine Industry Press, 1988. 58－60.(in Chinese)
[15] ZHANG Bang-wen, DENG Kang, LEI Zuo-sheng, et al. A mathematical model on coulped coalescence and removal of inclusion particles in continuous casting tundish [J]. Acta Metall Sinica, 2004, 40(6): 623－628. (in Chinese)
Foundation item: Project (50174037) supported by the National Natural Science Foundation of China; Project (50225416) supported by the National Science Fund for Distinguish Young Scholars
Correspondence author: ZHANG Bang-wen; Tel: +86-27-87556544; E-mail: bang1973@sina.com
(Edited by LONG Huai-zhong)
