­­Optimization of press bend forming path of aircraft integral panel

YAN Yu(阎 昱), WAN Min(万 敏), WANG Hai-bo(王海波), HUANG Lin(黄 霖)

School of Mechanical Engineering and Automation, Beihang University, Beijing 100191, China

Received 9 December 2008; accepted 10 March 2009

Abstract: In order to design the press bend forming path of aircraft integral panels, a novel optimization method was proposed, which integrates FEM equivalent model based on previous study, the artificial neural network response surface, and the genetic algorithm. First, a multi-step press bend forming FEM equivalent model was established, with which the FEM experiments designed with Taguchi method were performed. Then, the BP neural network response surface was developed with the sample data from the FEM experiments. Furthermore, genetic algorithm was applied with the neural network response surface as the objective function. Finally, verification was carried out on a simple curvature grid-type stiffened panel. The forming error of the panel formed with the optimal path is only 0.098 39 and the calculating efficiency has been improved by 77%. Therefore, this novel optimization method is quite efficient and indispensable for the press bend forming path designing.

Key words: aircraft integral panel; press bend forming path; neural network response surface; genetic algorithm; optimization

1 Introduction

As a traditional forming method for aircraft integral panels, press bend forming possesses many advantages, such as low tooling cost, short cycle time and adaptability to different contours[1]. Based on the three-point bending principle, press bend forming process performs multi-step bending with universal dies according to planned paths to form single or compound curvature contours.

The critical factor to form the contour of the panels is the bending path, which includes the bending position and the punch displacement. In many aircraft companies, the planning of press bend forming path simply depends on the intuitions of the operators, who carry out numerous trial and error tests. Since the relation between the forming path and the objective shape is rather complicated and the flat panel is very expensive, the trial and error method will certainly lead to great loss of money and time. Therefore, the optimization of the press bend forming path is rather essential. Academic research on the optimization of metal forming process using FE simulations is gaining more and more attention. Many metal forming processes are considered: deep drawing[2-5], hydroforming[6-8], superplastic forming [9-10], extrusion[11], forging[12-14], and several other processes[15-16]. However, few attempts have been made to optimize the press bend forming of aircraft integral panels. A new method for solving this problem is proposed in this work.

Genetic algorithm(GA) is an adaptive search method based on Darwinian principles of natural selection, survival of the fittest, and natural genetic phenomena. With strong capability in optimizing functions with unknown dependence on design variables, GA has been widely used in many optimization problems[17]. GA is able to search very large solution spaces efficiently, since it uses probabilistic transition rules instead of deterministic ones and most effectively applied to problems in which small changes result in very nonlinear behavior in the solution space[18]. But, the optimization of press bend forming process by the GA method only is rather inefficiently numerous; runs of FEM analysis are needed; and each run of FEM simulation always takes several weeks.

The response surface methodology, RSM, is an optimization method which uses approximations of the objective and constraint functions. The approximations are based on functional evaluations at selected points in the design space[19]. By using the response surface to replace the iterations of FEM analyses, the optimization efficiency could be greatly enhanced. However, prediction based on the polynomial equation commonly used in RSM, is often limited to low levels, resulting in poor estimations of optimal formulations[20]. Artificial neural network(ANN) has a considerable capability of mapping the nonlinear relationship between the input and the output that cannot be efficiently predicted by analytical or conventional statistical models[21-22]. It has been proved that neural network response surfaces have higher precision than polynomial response surfaces [23-26].

The goal of this work is to develop an integrated approach using FEM equivalent model[27], artificial neural networks(ANN) and genetic algorithms(GA) for optimum path design of press bend forming. Then, an example is presented to verify this novel optimization method.

2 Theoretical background

2.1 BP neural network response surface

BP network is a feed-forward back propagation (BP) multilayer network. The artificial neurons are organized in layers with one or more intermediate hidden layers placed between the input layer and output layer, sending their signals “forward”. First, the network obtains some information signals by the input layer; and the output produced from the first layer is then fed subsequently into the second layer and so on. The errors are then propagated backward[17]. The standard BP algorithm is

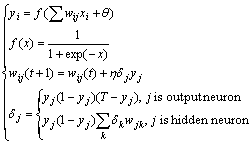     (1)

where t is the iteration number; x_i is the input of the neuron; y_i is the actual output of the neuron; f (?) is the Sigmoid function; θ is the bias of the neuron; w_ij is the connection weight of neuron i and neuron j; η is the learning rate; δ_j is the error of each neuron; and T is the expected output.

According to Kosmagoro theory, a three-layer BP network can approximate any continuous function when the proper structures and weights are provided. Therefore, in this work, a three-layer model using a back propagation(BP) algorithm is chosen.

The network adjusts its parameters by learning and training the data samples, by which the neural network’s accuracy in foreseeing the performance is decided. So, it is crucial to determining the proper range of data to be used for training with a good experimental design method. Taguchi method uses a special set of arrays called orthogonal arrays to arrange experiments. These standard arrays stipulate the way of conducting the minimal number of experiments to give the full information of all the factors[28]. With this experimental design method, the calculation time can be greatly reduced and the “over learning” of the network can be avoided. Hence, FEM simulations are conducted according to the Taguchi experimental design method to gain the training data samples.

2.2 Genetic algorithm

The mathematical model of optimization generally consists of the objective function, design variables, the constraints, and the optimizing algorithm. The mathematical expression is

         (2)

where f(x) is the objective function; n is the number of design variables; m is the number of the constraint function g_j(x); x_imin and x_imax are the upper and the lower constraints of the design variable x_i, respectively.

The genetic algorithm based on natural selection is a method for solving both constrained and unconstrained optimization problems, and a process driving beiological evolution. It is well known that GA is able to find the global optimization point, and the results of this algorithm are more reliable than those of the common methods of optimization. Furthermore, it is good for optimizing the “Black Box” problem, such as the trained neural network.

The genetic algorithm repeatedly modifies a population of individual solutions. At each step, the genetic algorithm selects individuals at random from the current population to be parents and uses them to produce the children for the next generation. Over successive generations, the population “evolves” toward an optimal solution. The genetic algorithm uses three main types of rules at each step to create the next generation from the current population. Selection rules select the individuals, called parents, which contribute to the population at the next generation. Crossover rules combine two parents to form children for the next generation. Mutation rules apply random changes to individual parents to form children. The basic GA is expressed as follows:

SGA=(C, E, P₀, M, Ф, Γ, Ψ, T)                (3)

where C is the coding method for individuals; E is the fitness function for individuals; P₀ is the initial random population; M is the size of the population; Ф is the selection function; Γ is the crossover function; Ψ is the mutation function; and T is the stopping criteria.

2.3 Equivalent model of press bend forming

FEM analysis seems to be disabled in the press bend forming of integrally stiffened panel research, because of the complexity of the integral panel structures, the multi-step process and the limitations of the hardware. So, we created equivalent models[27] to conduct simulations and optimizations more efficiently.

Plastic equivalent plate is a plate made of a virtual material that forms the similar shape as the detailed model when being formed with the same bending path. The virtual material with special plastic characteristics is obtained by in-depth analysis of the bending and springback mechanics of the detailed models. The key factor in calculating the virtual material parameters is to ensure that both models yield at the same punch displacement and possess the same outer radius after springback. FEM simulation results indicate that at the same punch displacement, the error of equivalent model is less than 6%, while the efficiency of FEM simulation has been improved by 80%[27]. So, it is possible to plan the forming path with much less modeling and calculation time than optimizing with the detailed models. The overall methodology for the forming path optimization of aircraft integral panels is shown in Fig.1.

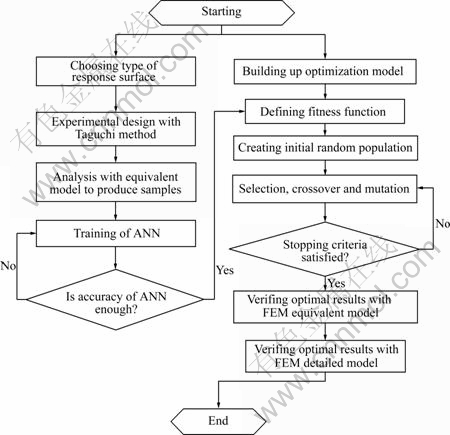
Fig.1 Flowchart of forming path optimization based on BP-GA algorithm

3 Optimization of press bend forming path

3.1 Description of optimization problem

A workpiece is designed according to typical structures of the real aircraft panels, the length of which is 500 mm. The material is aluminum alloy 7B04-T7451. The radii of the punch and the die are both 35 mm, and the die gap is 100 mm, as shown in Fig.2.

Fig.2 Sketch map of press bend forming process

Press bend forming is conducted at three positions, and the distances between the bending positions are 100 mm. The objective shape of this three-step forming is an arc with the radius of 1 430 mm and the centre angle of 16?. As shown in Fig.3, the whole arc represents the outer surface of the workpiece. With the three bending positions as the centers, three 160 mm-long (arc length) sections are chosen symmetrically to measure the arc heights. The arc heights are h₁, h₂ and h₃, which represent the arc heights of the three sections, respectively. From the geometry point of view, the ideal arc height of each section is: h=2.294 6 mm.

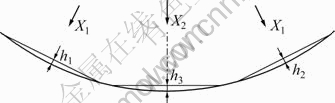
Fig.3 Sketch map of press bend forming path optimization problem

3.1.1 Objective function

The press bend forming error is taken as the objective function of this optimization problem, and the forming error is defined as

                     (4)

where  is the relative arc height error of the left section;  is the relative arc height error of the right section; and  is the relative arc height error of the middle section.

3.1.2 Design of variables

Press bend forming is a multi-step forming process. If the bending positions of press bend forming are too close to each other, the influence among different bending steps could be so remarkable that the deformation areas may overlap each other. So, punch displacement at any position will make a contribution to the final shape. In order to get the symmetric shape, the punch displacement at the left and the right section should be the same. Assuming the side punch displacement as X₁, and the middle punch displacement as X₂, as shown in Fig.3, X₁ and X₂ are taken to be design variables of this optimization problem.

3.1.3 Constraints

The punch displacements commonly adopted in factories are around 5 mm. The one step press bend forming FEM model with the punch displacement of 3, 4, 5 and 6 mm are set up to choose the range of the punch displacement. The calculated arc heights are 1.12, 1.90, 2.71 and 3.55 mm, respectively. And buckling begins to appear on the stiffeners when the punch displacement reaches 6 mm. By considering both the ideal arc height and the forming quality, the constraints of the design variables are selected:

                              (5)

3.2 FEM modeling of multi-step press bend forming

FEM analysis techniques allow taking benefit from predictions of simulation methods to determine the optimal bend forming path. In order to enhance the calculation efficiency, an FEM equivalent model of press bend forming of integrally stiffened panels is established. When the material parameters of the plastic equivalent plate are calculated, Eq.(6) needs to be satisfied and the detailed model and the equivalent model should yield at the same punch displacement to get the same contours after springback:

R_2E=R_2D                                     (6)

where R_2E is the bending radius of the outer surface of the plastic equivalent plate after springback, and R_2D is the bending radius of the outer surface of the detailed model after springback[27]. The parameters of the virtual material calculated using the method proposed in our previous study[27] are as follows: the yield stress(σ_sE) is 303.397 MPa; the hardening exponent(n_E) is 0.629; and the hardening coefficient(K_E) is 1 220.213.

The simulations are carried out using the commercial code ABAQUS. Press bend forming is a multi-step forming process, and the springback takes place continually. In order to improve the simulation accuracy and avoid constantly transferring between the explicit and implicit algorithms, both the forming and springback processes are simulated with ABAQUS/ Standard. The workpiece is modeled with solid elements C3D8R. The enhanced hourglass control approach is chosen. The tools are modeled with discrete rigid surfaces. As shown in Fig.4, by moving the punch and the dies, press bending and springback at different positions are accomplished.

Fig.4 Mises stress distribution of multi-step press bend forming process: (a) End of first bending; (b) End of first springback; (c) End of second bending; (d) End of second springback; (e) End of third bending; (f) End of third springback

3.3 Development of neural network response surface

The neural network response surface requires training with FEM experimental data to map the relationships between the punch displacements and the forming errors. The orthogonal test matrix L₂₅(5⁶) is adopted to carry out the experimental design. The side punch displacement X₁ and the middle punch displacement X₂ are taken as the two experiment factors, and the forming error e_shape defined in Eq.(4) as the experiment target. The factors and levels of the Taguchi method are shown in Table 1.

Table 1 Experimental layout of orthogonal test

Twenty datasets are rationally selected to be training samples, and the other five datasets to be testing samples. Training is accomplished using the BP algorithm. A three-layer network is developed, with the Tan-Sigmoid transfer function in the hidden layer and the linear transfer function in the output layer. The network should have two input neurons because there are two design variables. Five neurons are used in the hidden layer, as shown in Fig.5.

Fig.5 Topological structure of BP neural network

The Levenberg–Marquardt back propagation algorithm avoids computing Hessian matrix when modifying the second-order training speed. This algorithm appears to be the fastest method for training moderate-sized feedforward neural networks, thus   LM is used for training. And the gradient descent with momentum weight and bias learning function (Learngdm) are used for learning. Learngdm calculates the weight change for a given neuron from the neuron’s input and error, the weight (or bias), learning rate, and momentum constant, according to gradient descent with momentum. MSE is taken as the network performance function,which measures the network’s performance according to the mean of squared errors:

              (7)

where N is the total number of training dataset; t_i is the training sample data; and a_i is the output of the neural network. As shown in Fig.6, the training error decreases rapidly to the appointed range.

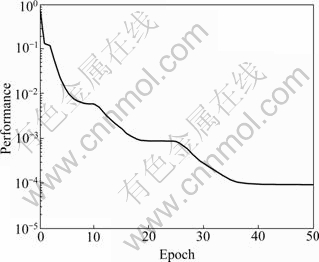
Fig.6 Training performance of neural network

After the neural network is trained, its accuracy should be examined in response to untrained inputs so as to specify the network’s accuracy in foreseeing the performance of the certain process. The five datasets that did not participate in the training are used to test the network. The outputs of the neural network and the Taguchi test results are shown in Table 2. It is observed that the relative errors for all the datasets are less than 6%, which means that the developed neural network is rather effective in mapping the relationship between the punch displacement and the press bend forming error(e_shape). Therefore, this neural network can appropriately substitute the time consuming FEM simulations in the GA optimization stage to enhance the optimization efficiency.

Table 2 Contrast between the output of neural network and Taguchi test results

The datasets with “*” marks are the testing datasets for the neural network, while the others are the training datasets.

The trained neural network response surface is shown in Fig.7, in which the small circle marks represent the sample data, and the position pointed out by the arrow is the place where the press bend forming error (e_shape) gets the minimum value.

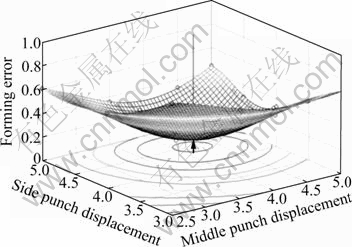
Fig.7 Sketch map of neural network response surface

3.4 Optimization with genetic algorithm

Fitness function is used to convert the objective function value to the corresponding fitness value. With the M-file describing the objective function, the trained neural network response surface is defined as the fitness function for the GA optimization. Rank scaling function, stochastic uniform selection function, elite count reproduction function, and Gaussian mutation function are adopted as the GA options. In this work, the size of the initial population is 30, and the crossover rate is 0.8. The stopping criteria is reached when X₁=4.47 mm, and X₂=4.22 mm. The output of the neural network with this input is: e_shape=0.083 298.

3.5 Verification with FEM analysis

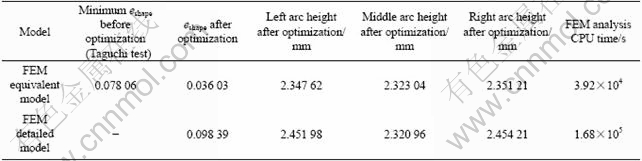
Verification of the optimal press bend forming path is carried out with both the FEM equivalent model and the FEM detailed model. The contrasts of the FEM analyses are shown in Table 3. According to the simulation results of the FEM equivalent model, it is obvious that the optimized path works much better than any press bend forming path used in the Taguchi test does. In addition, this optimal path also works well with the detailed model, and the forming error (e_shape) is only 0.098 39. The forming result indicates that the equivalent model performs quite well in the aspect of “equivalent”, and the differences between the two models are less than 4.25%. The calculating efficiency of it has been improved by 77%.

Table 3 FEM verification of optimal bending path

As shown in Fig.8, not only the shape accuracy but also the surface quality is ensured by the optimal path of press bend forming. The surface of the stiffened panel is smooth with no buckling on the stiffeners, and the shape is well symmetrically formed.

Fig.8 Equivalent plastic strain distribution of detailed model:  (a) Front view; (b) Isometric drawing

Considering the width to thickness ratio, the bending deformations of the stiffener and the skin are narrow plate bending and wide plate bending, respectively. So, the stiffener is under the plane stress condition, while the skin is under the plane strain condition. Compared with the outer surface of the skin, the normal bending stress of the stiffener top is larger, as it is farther from the neutral surface. In addition, the compression stress from the punch is substantial. As a result, the plastic deformation appeared first at the stiffener top. Because the curvature of the aircraft wing panel is usually very small, the punch displacement is not large. Therefore, most of the material of the specimen does not experience plastic deformation, as shown in Fig.8. And the final curved shape is owing to the plastic deformation of the stiffeners.

4 Conclusions

1) The application of the FEM equivalent model ensures fast optimization of the bend forming path. Compared with the detailed model, the computation efficiency of the equivalent model has been improved by 77%, and the differences between the two models are less than 4.25%. Thus, the total calculation time of the FEM Taguchi experiments can be dramatically reduced.

2) The developed neural network response surface has a strong mapping ability for press bend forming process of aircraft integral panels. It acts as a good substitute for the time consuming FEM simulations in the GA optimization, and achieves the goal of optimization with much less runs of FEM calculations.

3) The precise quantitative results of this study show that the FEM equivalent model, neural network response surface and their combination with the GA can realize the fast optimization of the press bend forming path, which is a pivotal problem in the aircraft integral panel manufacturing. Furthermore, this work provides a valuable research method for the optimization of other complicated forming processes.

References

[1] MUNROE J, WILKINS K, GRUBER M. Integral airframe structures(IAS)—Validated feasibility study of integrally stiffened metallic fuselage panels for reducing manufacturing costs, NASA/CR-2000-209337 [R]. Washington: Boeing Commercial Airplane Group, 2000.

[2] KLEINERMANN J, PONTHOT J. Parameter identification and shape/process optimization in metal forming simulation [J]. Journal of Materials Processing Technology, 2003, 139(1/3): 521-526.

[3] JANSSON T, ANDERSSON A, NILSSON L. Optimization of draw-in for an automotive sheet metal part—An evaluation using surrogate models and response surfaces [J]. Journal of Materials Processing Technology, 2005, 159: 426-434.

[4] LIEW K, TAN H, RAY T, TAN M. Optimal process design of sheet metal forming for minimum springback via an integrated neural network evolutionary algorithm [J]. Structural and Multidisciplinary Optimization, 2004, 26: 284-294.

[5] SHENG Z, JIRATHEARANAT S, ALTAN T. Adaptive FEM simulation for prediction of variable blank holder force in conical cup drawing [J]. International Journal of Machine Tools and Manufacture, 2004, 44: 487-494.

[6] FANN K, HSIAO P. Optimization of loading conditions for tube hydroforming [J]. Journal of Materials Processing Technology, 2003, 140(1/3): 520-524.

[7] AYDEMIR A, de VREE J, BREKELMANS W, GEERS M, SILLEKENS W, WERKHOVEN R. An adaptive simulation approach design for tube hydroforming processes [J]. Journal of Materials Processing Technology, 2005, 159: 303-310.

[8] JOHNSON K, NGUYEN B, DAWIES R, GRANT G, KHALEEL M. A numerical process control method for circular-tube hydroforming prediction [J]. International Journal of Plasticity, 2004, 20: 1111-1137.

[9] KIM Y, LEE J, HONG S. Optimal design of superplastic forming processes [J]. Journal of Materials Processing Technology, 2001,112(2/3): 166-173.

[10] CARRINO L, GIULIANO G, NAPOLITANO G. A posteriori optimization of the forming pressure in superplastic forming processes by the finite element method [J]. Finite Elements in Analysis and Design, 2003, 39: 1083-1093.

[11] ZOU L, XIA J C, WANG X Y, HU G A. Optimization of die profile for improving die life in the hot extrusion process [J]. Journal of Materials Processing Technology, 2003, 142(3): 659-664.

[12] ZHAO G, MA X, ZHAO X, GRANDHI R. Studies on optimization of metal forming processes using sensitivity analysis methods [J]. Journal of Materials Processing Technology, 2004, 147: 217-228.

[13] ANTO′NIO C, CASTRO C, SOUSA L. Optimization of metal forming processes [J]. Computers and Structures, 2004, 82: 1425-1433.

[14] CASTRO C, ANTO′NIO C, SOUSA L. Optimization of shape and process parameters in metal forging using genetic algorithms [J]. Journal of Materials Processing Technology, 2004, 146: 356-364.

[15] PALANISWAMY H, NGAILE G, ALTAN T. Optimization of blank dimensions to reduce springback in the flexforming process [J]. Journal of Materials Processing Technology, 2004, 146: 28-34.

[16] OHATA T, NAKAMURA Y, KATAYAMA T, NAKAMACHI E. Development of optimum process design system for sheet fabrication using response surface method [J]. Journal of Materials Processing Technology, 2003, 143/144(1): 667-672.

[17] LEE H W, ARUNASALAM P, LARATTA W P. Neuro-genetic optimization of temperature control for a continuous flow polymerase chain reaction microdevice [J]. Journal of Biomechanical Engineering, 2007, 129(8): 540-547.

[18] ADINEH V R, AGHANAJAFI C, DEHGHAN G H, JELVANI S. Optimization of the operational parameters in a fast axial flow CW CO₂ laser using artificial neural networks and genetic algorithms [J]. Optics & Laser Technology, 2008, 40(8): 1000-1007.

[19] JANSSON T, NILSSON L. Optimizing sheet metal forming processes—Using a design hierarchy and response surface methodology [J]. Journal of Materials Processing Technology, 2006, 178: 218-233.

[20] TAKAYAMA K, FUJIKAWA M, OBATA Y, MORISHITA M. Neural network based optimization of drug formulations [J]. Advanced Drug Delivery Reviews, 2003, 55: 1217-1231.

[21] MANDAL S, SIVAPRASAD P V, VENUGOPAL S. Artificial neural network modeling of composition-process-property correlations in austenitic stainless steels [J]. Materials Science and Engineering A, 2008, 485: 571-580.

[22] SADEGHI B H M. A BP-neural network predictor model for plastic injection molding process [J]. Journal of Materials Processing Technology, 2000, 103(3): 411-416.

[23] SHYY W, TUCKER P K, VAIDYANATHAN R. Response surface and neural network techniques for rocket engine injector optimization [J]. Journal of Propulsion and Power, 2001, 17: 391-401.

[24] PAL S, PAL S K, SAMANTARAY A K. Artificial neural network modeling of weld joint strength prediction of a pulsed metal insert gas welding process using arc signals [J]. Journal of Materials Processing Technology, 2008, 202: 464-474.

[25] KURTARAN H. A novel approach for the prediction of bend allowance in air bending and comparison with other methods [J]. Int J Adv Manuf Technol, 2008, 37: 486-495.

[26] CHENG J, LI Q S, XIAO R C. A new artificial neural network-based response surface method for structural reliability analysis [J]. Probabilistic Engineering Mechanics, 2008, 23(1): 51-63.

[27] YAN Yu, WAN Min, WANG Hai-bo. FEM equivalent model for press bend forming of aircraft integral panel [J]. Transactions of Nonferrous Metals Society of China, 2009, 19(2): 414-421.

[28] FOWLKES W Y, CREVELING C M. Engineering methods for robust product design [M]. Massachusetts, MA: Addison Wesley Longman, Inc, 1995.

(Edited by YANG Hua)