DOI: 10.11817/j.issn.1672-7207.2015.04.018

全数字差拍频率测量方法

朱祥维，龚航，黄新明，欧钢

(国防科技大学 电子科学与工程学院，湖南 长沙，410073)

摘要：针对目前卫星导航系统中原子频率标准的高精度频率测量需求，提出一种全数字差拍频率测量方法，对被测标准频率信号直接进行数字采样，以解决模拟差拍频率测量方法受温度影响大的问题。利用最大似然估计实现相位估计，采用相位差分完成频率测量，并引入小波阈值去噪处理进一步提高相位估计精度。研究结果表明：当测量间隔为1 s、估计点数为3 000时的频率测量精度为2.0×10^-14 /s，经过小波阈值去噪处理后频率测量精度达到10^-15 /s量级。

关键词：频率测量；差拍；相位估计；小波阈值去噪

中图分类号：TF803.21             文献标志码：A         文章编号：1672-7207(2015)04-1296-06

All-digital beat-frequency measurement method for precise frequency standard comparison

ZHU Xiangwei, GONG Hang, HUANG Xinming, OU Gang

(School of Electronic Science and Engineering, National University of Defense Technology, Changsha 410073, China)

Abstract: An all-digital beat-frequency measurement method was proposed to meet high measurement requirement of atomic oscillators widely used in global position system. The measurement frequency signal was directly sampled without any analogue processing to avoid the influence on environment. The method adopted the maximum likelihood estimation (MLE) to acquire phase estimation values, and frequency measurement was realized by phase difference estimation. The wavelet threshold de-noising was introduced to improve the precision of phase estimation. Performance of the method was analyzed and verified by simulation. The results show that when the frequency measurement precision reaches 2.0×10^-14 /s and  measurement points reaches 3 000, the frequency measurement precision reaches 10^-15 /s order with wavelet threshold de-noising.

Key words: frequency measurement; beat-frequency; phase estimation; wavelet threshold de-noising

随着卫星导航系统的发展，其定位精度越来越高，相应频率标准的准确度和稳定性提高得非常快，目前导航系统中所用的原子频率标准的秒级稳定度能达到10^-15/s甚至更高，相应地对精密频率测量方法的测量精度提出了较高要求^[1-2]。卫星导航系统中使用的原子频率标准属于精密频率标准，精度较高，对测量方法、测量设备及测量环境等条件要比普通频率测量要求高得多。常用的精密频率标准测量方法包括相位比对法、拍频法和双混频器时差测量等^[3-4]。其中，相位比对法常常被用于频标准确度和长期指标的比对，后2种方法主要用于短期稳定度的比对。比相法广泛地用于频率准确度和长期稳定度的测量，可以达到很高的比对精度，比对的相对误差为10^-16 /s量级。由此可以用来测量频率稳定度、频率的长短期指标等，但比相法的时间响应比较慢，难以用在短期指标比对中。双混频时差测量的精度较高，对时间间隔的测量要求不高，但是其测量精度受到放大器、混频器噪声的限制^[4]。差拍法具有较高的频率测量分辨率，方案简单、精度高，通过拍频后测量精度提高了差拍因子倍，并且计数器只需要检测低频信号，有利于计数器的实现，但计数器的时标精度以及由于对信号整形引入的误差、设备本底噪声等限制了测量精度的提高^[4]。鉴于差拍测量方法的这些特性，可以考虑对差拍频率测量的实现结构进行重新设计，采用数字化方法进行改进^[5-7]。若改进后能够提高测量精度，则数字化后的差拍测频法与其他方法相比，将具有较高频率测量分辨率以及方案简单的优势。文献[4，8]提出了基于虚拟仪器的差拍频率计，虽然测量精度达到了10^-14 /s，但实现方案中仍然包含模拟混频等模块，没有充分体现数字化的优势。为此，本文作者提出一种全数字化差拍频率测量方法，通过数字信号处理技术，完成高精度频率测量。

1  差拍频率测量法

差拍频率测量是一种通过普通的周期计数器获得高分辨率的经典频率测量方法^{[4, 8]}，其基本原理是模拟混频及周期计数，将待测信号与作为参考的基准频率信号进行混频处理，以得到待测信号相对于参考信号的频差信号即差拍信号。由于差拍信号频率较低，故可以采用普通计数器对差拍信号周期进行计数以实现对频率进行测量。差拍频率测量法通过提取待测信号相对于参考信号的相位差信息作为差拍信号，得到的差拍信号频率远小于原待测信号，因此，与直接测频法相比，大大提高了测量分辨率。差拍频率测量法的原理如图1所示。混频器两端输入的信号先经过放大器调理，然后得到叠加了噪声和多次谐波的差拍信号， 通过低通滤波器滤除谐波和噪声，最后用周期计数器测量。

图1  差拍频率测量法原理框图

Fig. 1  Schematic diagram of beat-frequency measurement method

由于混频对频率的下变频作用，可以将频率测量分辨率提高差拍因子倍。例如，当待测频率标称值f_x为10 MHz，参考频率f_r为10 Hz至10 MHz时，混频后的差拍信号频率F=10 Hz，若计数器时标为0.1 μs，则由计数器误差引起的周期测量相对误差Δτ为

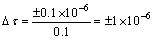          (1)

则差拍因子为

            (2)

总分辨率为

            (3)

在上述条件下，差拍频率测量法较直接用计数器将分辨率提高了差拍因子倍。

差拍频率测量法主要误差来源除了计数器引入的触发误差、计数误差外，还应该包括混频器、低通滤波器等器件引入的噪声对测量结果的影响。

2  全数字精密频率测量方法

2.1  测量原理

全数字精密频率测量方法的实现框图如图2所示。采用直接采样的方式实现全数字化测量，在数字端对待测信号进行混频处理，得到差拍信号，然后通过数字信号处理的方法实现精密频率测量。数字域上的测频是通过相位估计实现的，即首先得到相位的估计值，然后利用相位差分得到频率估计值。

设待测频率标称值f_x，参考频率为f_r，混频后的差拍信号频率f_p=f_x-f_r。对被测信号采样后，信号可以表示为

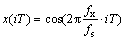           (4)

其中：f_s为采样频率；T为离散采样点间隔。经过混频合路得到的差拍信号可以表示为

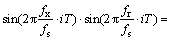
     (5)

对差拍信号的I/Q支路分别进行低通滤波和抽取等操作，然后对差拍信号进行频率估计从而完成频率测量。数字化精密频率测量通过相位估计完成频率的精密测量，数字精密频率测量的原理图如图3所示。

图2  数字化差拍频率测量法原理框图

Fig. 2  Schematic diagram of digital beat-frequency measurement method

图3  数字精密频率测量的原理示意图

Fig. 3  Schematic diagram of digital precise frequency measurement

设1次测量间隔T期间估计的2个相位值分别为θ₁及θ₂，1次测量周期含有L个差拍周期，则数字域上测量得到的差拍频率可表示为

        (6)

其中：为测得的整数倍差拍频率部分；为通过相位估计值差分得到的精密频率测量值。从式(6)可以看出：若获得了差拍频率测量值，则结合参考频率f_r，可以得到待测频率的频率测量值为。

可以看出频率估计的精度和相位估计精度直接相关，下面分析相位估计方法及其精度，然后介绍频率估计方法及其精度，从而得出新方法的测量精度。

2.2  相位估计方法

采样得到的信号是正弦信号，因此，本文的相位估计问题是高斯白噪声下的已知幅度和频率的正弦信号的相位估计问题。相位估计可以采用最大似然估计(MLE)，该方法可视为渐进无偏的和渐进达到CRLB，因此，它是渐进最佳的。根据文献[9-10]，正弦信号相位的MLE可以近似表示为

       (7)

同样根据文献[9]，离散采样下频率已知正弦信号的相位估计方差为

            (8)

其中：A为信号幅度；N为用于估计的采样点数；σ²为高斯白噪声方差；相位估计时的信噪比。

2.3  频率估计方法

得到相位估计值后，就可以对频率进行估计。本文利用相位差分实现频率估计。值得说明的是：这里估计的频率为差拍信号的频率，待测频率的频率还需要加上参考频率。设前、后2次的测量间隔为T，测量相位估计值为及，则频率估计值可以表示为

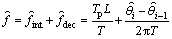        (9)

频率估计值分为2部分：整数频率部分为整数倍的标准差拍频率，可以通过测量间隔和差拍频率确定；小数频率部分为1个标准差拍频率以内的频率估计值。可以看出频率测量精度主要由小数频率估计精度决定。

根据式(8)，可以得到频率估计值的方差为

     (10)

2.4  频率测量精度

上面给出了数字域上进行相位估计和频率估计的方法和精度分析，下面分析全数字化差拍频率测量方法的测量精度。

定义频率测量精度为频率测量值减去频率真实值然后除以频率真实值的均方根，则本文提出的数字化差拍频率测量方法的频率测量精度为

       (11)

从式(11)可以看出：全数字差拍频率测量方法的测量精度与输入信噪比R_SN、用于相位估计的点数N以及测量间隔有关。输入信噪比越大，则测频精度越高。类似地，用于相位估计的点数N越多、测量间隔越大，测频精度越高。下面的数值仿真部分将通过仿真分析验证这些因素对测频精度的影响。

上面诸多因素中，R_SN由ADC决定。ADC量化噪声会导致信噪比降低，进而影响相位估计精度。ADC量化引入的噪声通常可以认为是一种加性白噪声。参考文献[11]，数字信号处理中经常使用的简化的等效计算公式为

     (12)

其中：b为ADC 的量化比特位；f_s为采样率；B为信号带宽。

现有的高性能ADC芯片有8位、12位、14位以及16位的，在本文的分析仿真中，ADC 量化位数统一取14 bits，不加幅度噪声和采样时钟噪声，在这种情况下得到的信噪比R_SN 约为86 dB。

2.5  小波阈值去噪

由式(11)可知：频率测量精度和采样信号的信噪比相关，若能够抑制采样信号中的噪声项，则能够有效提高测量精度。小波去噪是通过小波变换分离出噪声或其他不需要的信息，从而实现降噪。小波去噪在信号预处理方面应用广泛，特别是小波阈值去噪易实现且效果良好。其基本思想基于如下假设：携带信息的原始信号在频域或小波域能量相对集中，表现为能量密集区域的信号分解系数绝对值较大，而噪声信号的能量谱相对分散，所以，其系数的绝对值小。这样，通过设定阈值的方法可以过滤掉绝对值小于一定阈值的小波系数，从而达到降噪的效果。

小波阈值去噪的具体实现方法可参考文献[12-13]。本文小波变换采用的小波基是SymletsA小波族中的sym4小波。

3  数值仿真

为了验证本文提出的全数字差拍频率测量方法，进行数值仿真验证，并与理论频率测量性能进行对比。输入频率为10 MHz标准频率信号，采样频率取为21 MHz。用于相位估计的点数及测量间隔均根据仿真条件设置。ADC 量化位数为14 bits，相应的信噪比约为86 dB。下面首先分析用于相位估计的点数N以及测量间隔与频率测量精度的关系，然后给出数字化测频方法的测量精度，最后仿真分析小波阈值去噪对测量精度的提升作用。需要注意的是：频率测量精度均是指数字域的频率估计精度，对于包括数字差拍处理在内的整个方法的测量精度，需要再除以差拍因子。

3.1  估计点数对测量精度的影响

由式(8)和(11)可知：用于相位估计的估计点数越多，相位估计精度就越高，频率测量精度就越高。为了仿真验证估计点数对频率测量精度的影响，在相同的输入信噪比条件下对估计点数分别为3 000，6 000，9 000和15 000条件下的频率测量精度进行数值仿真，其中测量间隔为1 s，仿真结果如表1所示。

由表1可知：用于相位估计的点数越多，频率测量值就越精确，这与理论结果是相符的；估计点数不同时的理论和仿真频率测量精度理论值与仿真值较吻合，估计点数为6 000，9 000及15 000时的频率测量精度分别是估计点数为3 000时的倍、倍以及倍。

表1  估计点数不同时的理论和仿真频率测量精度

Table 1  Theoretical and actual frequency measurement accuracy under different measurement numbers

3.2  测量间隔对测量精度的影响

测量间隔为1，2，3以及5 s时的频率测量精度如表2所示，仿真条件与前述仿真类似，其中估计点数为3 000。从表2可以看出：随着测量间隔的增加，相位估计精度越高，频率测量值也越来越精确；同时，理论频率精度与频率仿真测量精度较吻合，测量间隔为2，3及5 s时的频率测量精度分别是测量间隔为1 s时的2倍、3倍以及5倍。

表2  测量间隔不同时的理论和仿真频率测量精度

Table 2  Theoretical and actual frequency measurement accuracy under different time intervals     Hz

3.3  测量精度

前面探讨了估计点数和测量间隔对测量精度的影响，下面给定估计点数和测量间隔，仿真验证本文提出的全数字差拍频率测量方法的测量精度。当测量间隔为1 s、估计点数为3 000时测量精度如图4、图5以及表3所示。

图4  相位估计误差值

Fig. 4  Phase estimation error values

图5  频率估计误差值

Fig. 5  Frequency estimation error values

表3  理论和仿真频率测量精度

Table 3  Theoretical and actual frequency measurement accuracy

从表3可以看出相位和频率估计精度都与其理论精度相近，证明了本方法的正确性。仿真结果表明：在给定条件下，本方法的频率测量精度为  2.018×10^-7 /s，若待测频率为10 MHz，则差拍因子为10⁷，可以得到本文提出的数字化频率测量方法测量精度为2.018×10^-14 /s。同时，可以推断出：若增加估计点数，则频率测量精度可以达到10^-15/s，满足当前高精度精密频率测量的需求。

3.4  小波阈值去噪对测量精度的影响

小波阈值去噪可以有效地降低白噪声的影响，提高频率测量值的估计精度。为了验证小波阈值去噪对测量精度的影响，对仿真得到的相位估计值进行小波去噪，得到去噪后的相位估计值和频率测量值如图6与图7所示。

从图6和图7可以看出：经过小波阈值去噪后，白噪声对测量结果的影响得到了充分抑制，使得测量精度提高1个数量级以上。同时，经过小波阈值去噪后的相位估计值和频率估计值在某些值上出现了较大波动，类似于吉布斯现象，这是由小波去噪时阈值的选取所致。通过改进相应的阈值选取可以减弱或避免这种现象，具体方法见文献[14-15]。

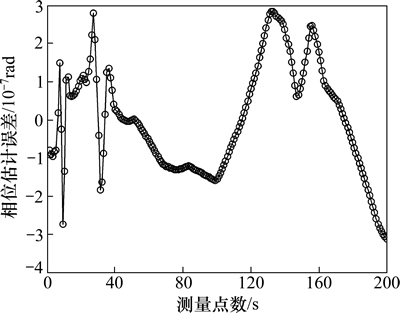
图6  小波阈值去噪后的相位测量值

Fig. 6  Phase measurement values with wavelet threshold de-noising

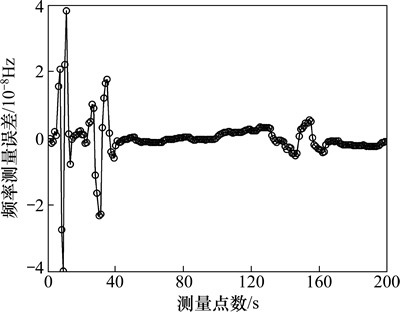
图7  小波阈值去噪后的频率测量值

Fig. 7  Frequency measurement values with wavelet threshold de-noising

4  结论

1) 提出了一种全数字差拍频率测量方法，采用全数字信号处理方法克服了模拟差拍频率测量方法受温度影响大的缺点。

2) 提出的频率测量方法的测量精度与输入信噪比、用于相位估计的点数以及测量间隔有关。输入信噪比越高，测频精度越高。同样，用于相位估计的点数越多、测量间隔越大，测频精度越高。

3) 当测量间隔为1 s、估计点数为3 000时，频率测量精度为2.0×10^-14 /s，经过小波阈值去噪处理后频率测量精度达到10^-15 /s量级。卫星导航系统中所用的频率基准(即原子钟)的最高精度大约为10^-15 /s，提出的数字化频率测量方法可以满足卫星导航系统中的精密频率测量需求。

参考文献：

[1] 刘娅. 多通道数字化频率测量方法研究与实现[D]. 西安: 中国科学院国家授时中心, 2010: 1-18.

LIU Ya. Research on and achieve multi-channel digital frequency measurement method[D]. Xi’an: Chinese Academy of Sciences. National Time Service Center, 2010: 1-18.

[2] Walls L, Allan D W. Measurements of frequency stability[J]. Proc IEEE, 1986, 74(1): 162-168.

[3] 刘娅, 李孝辉, 王玉兰. 一种基于数字技术的多通道频率测量系统[J]. 仪器仪表学报, 2009, 30(9): 1963-1968.

LIU Ya, LI Xiaohui, WANG Yulan. Multi-channel frequency measurement system based on digital signal processing[J]. Chinese Journal of Scientific Instrument, 2009, 30(9): 1963-1968.

[4] 李孝辉, 杨旭海, 刘娅, 等. 时间频率信号的精密测量[M]. 北京: 科学出版社, 2010: 104-144.

LI Xiaohui, YANG Xuhai, LIU Ya, et al. Precision measurement of frequency and time[M]. Beijing: Publishing House of Science, 2010: 104-144.

[5] Sojdr L, Cermakj, Brida G. Comparison of high-precision frequency-stability measurement systems[C]//Proceedings of the 2003 IEEE International Frequency Control Symposium.Tampa, FL, 2003: 317-325.

[6] Mochizuki K, Uchino M, Morikawa T. Frequency-stability measurement system using high-speed ADCs and digital signal processing[J]. IEEE Transactions on Instrumentation and Measurement, 2007, 56(5): 1887-1893.

[7] Uchino M, Mochizuki K. Frequency stability measuring technique using digital signal processing[J]. Electronics and Communications in Japan, 2004, 87(1): 21-33.

[8] LIU Ya, LI Xiaohui, WANG Wenli, et al. Research and realization of portable high-precision frequency set[J]. Computer Measurement & Control, 2008, 16(1): 21-23.

[9] Kay S M. Fundamentals of statistical signal processing, Volume 1: estimation theory[M]. NJ: Englewood Cliffs, 1998: 3035.

[10] ZHU Xiangwei, SUN Guangfu, YONG Shaowei, et al. A high-precision time interval measurement method using phase-estimation algorithm[J]. IEEE Transactions on Instrumentation and Measurement, 2008, 57(11): 2670-2676.

[11] Oppenheim A V, Schafer R W. Discrete-time signal processing [M]. 2nd ed. New Jersey, USA: Prentice-Hall Inc, 1999: 234-250.

[12] 王宏强, 尚春阳, 高瑞鹏, 等. 基于小波系数变换的小波阈值去噪算法改进[J]. 振动与冲击, 2011, 30(10): 165-168.

WANG Hongqiang, SHANG Chunyang, GAO Ruipeng, et al. An improvement of wavelet shrinkage denoising via wavelet coefficient transformation[J]. Journal of Vibration and Shock, 2011, 30(10): 165-168.

[13] Jansen M, Bultheel A.Multiple wavelet threshold estimation by generalized cross validation for images with correlated noise[J]. IEEE Transactions on Image Processing, 1999, 87(7): 947-953.

[14] 曹晓英, 张智军, 向建军. 基于提升小波改进阈值的雷达信号去噪方法[J]. 计算机工程与应用, 2012, 48(14): 143-147.

CAO Xiaoying, ZHANG Zhijun, XIANG Jianjun. Method of radar signal de-noising based on lifting wavelet improved threshold[J]. Computer Engineering and Application, 2012, 48(14): 143-147.

[15] 薛伟, 关福宏, 陈良章, 等. 基于一种新的小波阈值函数的雷达信号去噪[J]. 计算机仿真, 2008, 25(8): 319-322.

XUE Wei, GUAN Fuhong, CHEN Liangzhang, et al. Radar signal de-noising based on a new wavelet thresholding function[J]. Computer Simulation, 2008, 25(8): 319-322.

(编辑  陈灿华)

收稿日期：2014-06-18；修回日期：2014-08-27

基金项目(Foundation item)：国家自然科学基金资助项目(61403413)(Project (61403413) supported by the National Natural Science Foundation of China)

通信作者：朱祥维，副研究员，从事卫星导航系统及时间同步技术研究；E-mail：zhuxiangwei@nudt.edu.cn