J. Cent. South Univ. (2017) 24: 1090-1097

DOI: 10.1007/s11771-017-3512-y

Comparison and assessment of time integration algorithms for nonlinear vibration systems

YANG Chao(杨超)^{1, 2}, YANG Bao-zhu(杨宝柱)¹, ZHU Tao(朱涛)¹, XIAO Shou-ne(肖守讷)¹

1. State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, China;

2. School of Mechanical, Electronic and Control Engineering, Beijing Jiaotong University, Beijing 100044, China

Central South University Press and Springer-Verlag Berlin Heidelberg 2017

Abstract: A corrected explicit method of double time steps (CEMDTS) was introduced to accurately simulate nonlinear vibration problems in engineering. The CEMDTS, the leapfrog central difference method, the Newmark method, the generalized-a method and the precise integration method were implemented in typical nonlinear examples for the purpose of comparison. Both conservative and non-conservative systems were examined. The results show that it isn’t unconditionally stable for the precise integration method, the Newmark method and the generalized-a method in nonlinear systems. The stable interval of the three methods is less than that of the CEMDTS. When a small time step (△t≤T_min/20) is employed, the precise integration method is endowed with the highest accuracy while the CEMDTS possesses the smallest computation effort. However, the CEMDTS becomes the most accurate one when the time step is large (△t≥0.3T_min) or the system is strongly nonlinear. Therefore, the CEMDTS is more applicable to the nonlinear vibration systems.

Key words: nonlinear vibration; conservative system; explicit algorithm; accuracy

1 Introduction

Most of the problems in engineering are nonlinear in essence. The superposition principle is invalid in the process of analyzing the dynamic response of nonlinear systems. As a result, the linear methods based on the superposition principle are no longer applicable in nonlinear systems. Special solving methods must be used to obtain reasonable results for strong nonlinear problems. There are two kinds of quantitative methods for nonlinear vibration problems, which are the approximate analytical method and the numerical method. The former is generally applied to weak nonlinear problems. For complex nonlinear vibration problems in engineering, especially the strong nonlinear problems, the numerical method is the only way.

The numerical method can be divided into the displacement method and the acceleration method in terms of the basic variables. It also can be divided into the explicit algorithm and the implicit algorithm according to the difference of solving processes. The central difference method and the ZHAI method are the representative ones of the explicit algorithm [1-3]. The implicit algorithm contains the linear acceleration method, the Wilson-q method, the Newmark method, the Houbolt method, the HHT-a method [4], the generalized-a method [5], etc. The implicit method usually generates convergence problems when it is applied to strong nonlinear vibration systems [6, 7]. The computation effort and the computational cost of the explicit algorithm are far less than those of the implicit method for solving transient problems and the problems of high frequency mode. In addition, the precise integration method (PIM) based on the Hamilton’s principle is another important numerical method for solving equations of motion [8, 9]. The PIM is very accurate for linear vibration systems. A modified PIM is developed for time-varying vibration systems [10]. The response of the modified PIM is compared with that of the central difference method. Some explicit integration algorithms have been developed with second order accuracy [11, 12]. The methods are compared with the Newmark explicit method and the average acceleration method in mild nonlinear systems. MASURI et al [13] summarized the existing time integration methods, and tried to put algorithmic designs under the umbrella of the generalized single solve single step framework.

The authors in this work focus on the second-order method, and the first-order method is not considered. The numerical methods with numerical damping are unsuitable for any applications involving integration over a long time duration, especially the conservative system [7]. The total energy is indeed conserved in conservative systems. However, the results of some numerical methods may be un-conserved and unstable. In order to simulate the nonlinear problems of long term response, we introduce an explicit method proposed by the author, which is the corrected explicit method of double time steps (CEMDTS) [14]. The accuracy, the stability and the computation effort of the CEMDTS and some other typical numerical methods are analyzed and compared in nonlinear vibration systems. The results show that the CEMDTS is more applicable to solving the problems of nonlinear vibration systems.

2 Equations of nonlinear vibration systems

The equation of motion of vibration systems is usually a second-order differential equation. If the change in structural mass is not considered, the equation of motion of a nonlinear vibration system can be expressed as

                          (1)

where M is the mass matrix; F and P are the force vectors; u and t are the acceleration, velocity, displacement and time, respectively.

In nonlinear vibration systems, the second term of Eq. (1) is usually a nonlinear term. The nonlinear factors are mainly the nonlinear restoring force and the nonlinear damping force. If the second term of Eq. (1) is rewritten as

                            (2)

where C and K represent the damping matrix and the stiffness matrix, respectively. Then, Eq. (1) is the commonly-used equation of motion of linear vibration systems.

The dynamic degree of nonlinearity can be used to describe the change in stiffness of a nonlinear system [11, 12]. This parameter is the ratio of the stiffness at any given moment and the minimum stiffness. The expression is

                                   (3)

where l_i, k_i and k_min are respectively the dynamic degree of nonlinearity, the stiffness at the ith time point and the minimum stiffness. Therefore, the instantaneous stiffness equals to the initial stiffness if l_i=1. The closer the l_i is to 1, the weaker the degree of nonlinearity of a vibration system is.

3 Time integration methods

Two time integration algorithms are presented in this section. The methods are the corrected explicit method of double time steps (CEMDTS) and the generalized-a method. The former is proposed by the author to solve the problems of nonlinear vibration systems. The latter is a famous integration method with controllable numerical damping. The detailed integration schemes of the leapfrog central difference method, the Newmark method and the precise integration method can be consulted in Refs. [7, 9, 15], respectively.

3.1 Corrected explicit method of double time steps

The corrected explicit method of double time steps is proposed by the author in reference [14]. Firstly, the differential equation of motion of a nonlinear vibration system is given as

                          (4)

The expressions of the velocity and the displacement are given as follows:

                (5)

where η is the integral parameter, which can be chosen in the range of [0,1]. The CEMDTS is equivalent to the leapfrog central difference method if η=0; when η=0.5, the CEMDTS degrades into the ZHAI method without numerical damping [1, 2].

The stability and the accuracy of the CEMDTS are analyzed in detail in Ref. [14]. The CEMDTS is conditionally stable. The product of the time step △t and the maximum circular frequency ω_max is required to be less than 2 in undamped systems. The highest accuracy of the CEMDTS is second-order. If the procedure starts with the starting accuracy is O(△t²) at least. In addition, the starting accuracy is if η=0.5. Therefore, this algorithm can be regarded as a self-start one. In a multiple degree-of-freedom vibration system, there is no need for iterations and matrix inversions in the calculation as long as the mass matrix can be converted to a diagonal matrix. The total computation effort can be greatly reduced.

3.2 Generalized-a method

The original version of the so-called generalized-a method is found to be firstly proposed by SHAO Hui-ping in 1988 [16, 17]. The expressions of the velocity and the displacement are the same as those of the Newmark method in the generalized-a method. They are given as

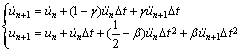       (6)

where b and g are the integral parameters; the subscript n represents the time t_n; △t is the time step.

The equation of motion of the generalized-a method possesses two undetermined coefficients. The nonlinear format of Eq. (7) is rewritten in Eq. (8):

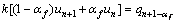            (7)

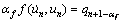                    (8)

where a_m and a_f are the undetermined coefficients. When a_m=a_f=0, the generalized-a method is equivalent to the Newmark method; When a_m=0, the generalized-a method is equivalent to the HHT-a method; When a_f=0, the generalized-a method is equivalent to the WBZ-a method. The unknown accelerationand the velocity in Eq. (6) are expressed by the basic displacement variable and the known physical quantities, and then they can be substituted into Eq. (8) to solve the equations.

4 Nonlinear examples

There are two typical nonlinear examples in this section, which are the pendulum with large amplitudes and the stiffness hardening vibration system. The two vibration systems are conservative. As a result, the numerical damping of algorithms is not desired for long-term simulations. The examples are conducted with the leapfrog central difference method (LCDM), the Newmark method, the generalized-a method (GaM), the precise integration method (PIM) and the CEMDTS. The Newmark method adopts the trapezoidal rule, namely b=0.25, g=0.5. The integral parameters of the equation of motion are a_m=a_f=0.5 for the generalized-a method, and the expressions of the velocity and displacement are the same as those of the Newmark method. The predictor- corrector integration scheme is employed in the precise integration method, in which the prediction method is the Lagrange interpolation formula [18]. In order to obtain high accuracy, the integral parameter of the CEMDTS is chosen as η=0.45. The conservative systems should comply with the law of conservation of energy. The small error produced by the numerical methods is permissible, but the results must be stable.

4.1 Nonlinear pendulum

If the amplitude of a pendulum is small, the vibration system can be regarded as a linear system. However, if the amplitude is large enough, the system is a nonlinear vibration system with the property of stiffness softening. As shown in Fig. 1, the pendulum is supported by a bar. The equation of motion can be given as follows:

Fig. 1 Nonlinear pendulum:

                               (9)

where and θ are the angular acceleration and the angular displacement, respectively; the acceleration of gravity is g=9.8 m/s²; l is the length of the bar, and its value is 9.8m. The maximum circular frequency is 1 rad/s. The initial condition 1 is θ(0)=-0.95 π, △t₁=0.3 s, and the end time t₁=15 s. The initial condition 2 is θ(0)=0, rad/s, △t₂=0.3 s, and the end time t₂=10 s. The time step is approximately 1/20 of the minimum natural period T_min.

The phase locus of the pendulum is taken as the exact solution. It is respectively compared with the results of the CEMDTS, the leapfrog central difference method (LCDM), the Newmark method, the generalized-a method (GaM) and the precise integration method (PIM). Figure 2 shows the phase locus of the pendulum under the initial condition 1. Divergence takes place in the results of the Newmark method and the generalized-a method, and the phase loci are snake-like. The results of other three methods are stable. In addition, the precise integration method is endowed with thehighest accuracy, and its result almost coincides with the exact solution. Moreover, the accuracy of the CEMDTS is higher than that of the LCDM. As shown in Fig. 3, the numerical result of the Newmark method diverges from the exact solution gradually. The results of other four methods are stable and reasonable. The result of the LCDM has the maximum error, and the CEMDTS follows. Nevertheless, the results of the generalized-a method and the precise integration method are more accurate.

Fig. 2 Phase locus of pendulum under initial condition 1

Fig. 3 Phase locus of pendulum under initial condition 2

4.2 Stiffness hardening system

Rubber springs, air springs and tension strings belong to hard springs in engineering. For instance, we consider an undamped nonlinear system with single degree-of-freedom. The stiffness characteristics of the system [19] are shown as follows:

k_b=k₀(1+au²)                                (10)

where k₀ is the initial stiffness; a is the nonlinear coefficient. The larger the nonlinear coefficient is, the higher the degree of nonlinearity of the system is. The initial values of system parameters are the lumped mass m=1 kg, the nonlinear coefficient a=30 and k₀=100 N/m. The initial condition is x(0)=1.5 m, The time step and the end time are △t=0.001 s and t_end=0.3 s. The initial circular frequency is 10 rad/s, and the maximum circular frequency is 82.76 rad/s. The time step is 1/76 of the minimum natural period.

Figure 4 shows the results of the CEMDTS, the LCDM, the Newmark method, the generalized-a method (GaM) and the precise integration method (PIM). The results of the integration schemes are respectively compared with the exact phase locus. The phase locus of the Newmark method damps as time goes on. So, the error is very great. However, the numerical results of the other four methods almost coincide with the exact solution. The energy is approximately conserved. The precise integration method possesses the highest accuracy, and the error of the LCDM is the largest.

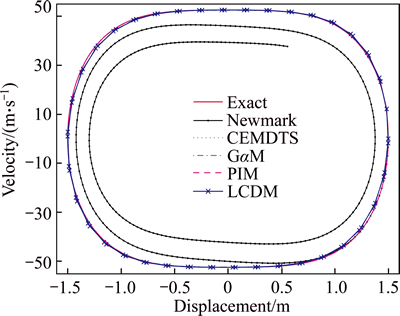
Fig. 4 Phase locus of a stiffness hardening system

5 Applications in engineering

Two applications are included in this section. One is the response of a tall shear building in earthquakes, and the other is the vertical vibration of a railway vehicle. The first system is conservative while the second one is non-conservative. The examples are conducted with the leapfrog central difference method (LCDM), the Newmark method, the generalized-a method (GaM), the precise integration method (PIM) and the CEMDTS. All the parameters of these algorithms are identical with those of the previous section.

5.1 Response of a shear building in earthquakes

The vibration system of a tall building in earthquakes can be simplified as a multi-stage shear beam model. The dislocations between stories can result in nonlinear stiffness. Assume that the function relationship of the stiffness and the relative displacement subjects to Eq. (10). There are six floors in the building which is shown in Fig. 5. The mass of each floor is m=10⁵ kg. The initial stiffness and the nonlinear coefficient are k₀=10⁸ N/m and a=10, respectively. The ground acceleration of an earthquake is 10sin(pt). The initial minimum circular frequency of the shear model is 7.62 rad/s. Its maximum circular frequency is 61.41 rad/s, and the corresponding minimum period is T_min=0.1 s.

Fig. 5 Model of a six-story building

The result of the LCDM with △t=0.0001 s is taken as the exact solution for the comparison purpose. Two time steps, which are △t=0.0007 s and △t=0.03 s, are employed in the CEMDTS, the Newmark method, the generalized-a method (GaM) and the precise integration method (PIM). This means that the time steps are 0.007T_min and 0.3T_min. The displacement responses of the bottom story and the top story are shown in Figs. 6 and 7, respectively. It is obvious in Fig. 6 that the results of the four methods are highly consistent with the exact solution when the time step is small. The accuracy of the precise integration method is the highest. The maximum relative displacement between stories is 0.094 m. The displacements of the top story are depicted in Fig. 7 under the condition of △t=0.03 s. The numerical results of the precise integration method are unstable when the time step is large. The result of the generalized-a method is close to that of the Newmark method, and the errors are slightly large. However, the error of the CEMDTS is the smallest under this condition.

When the time step is △t=0.0001 s, the CPU time consumed by the CEMDTS, the Newmark method, the generalized-a method and the precise integration method are 1.89 s, 2.01 s, 2.23 s and 11.12 s, respectively. It means that the computation effort of the precise integration method is the largest. However, the computation effort of the CEMDTS is the smallest.

Fig. 6 Displacement response of bottom story (△t=0.0007 s)

Fig. 7 Displacement response of top story (△t=0.03 s)

5.2 Vibration of a railway vehicle

The vertical vibration of a railway vehicle can be described by the classical dynamical model shown in Fig. 8. The model is composed of four wheel sets, two bogie frames and one carbody. There are 7 degrees of freedom (DOFs) of vertical movement for the 7 rigid bodies and 3 pitching DOFs for the bogie frames and the carbody. The total DOFs of the vertical model is 10. The detailed parameters of the model are obtained in reference [20]. The nonlinear factor is the contact force of wheel-rail defined as follows:

               (11)

where x_w and x_r are the vertical displacements of the wheel and the rail, respectively; G is a constant. The contact stiffness increases with the increasing penetration.

Fig. 8 Vertical model of a railway vehicle

The case of wheel-rail impacting is considered here. The initial displacements of all rigid bodies are 0. The initial velocity of the carbody is 0, and the initial velocity of the bogie frames and the wheel sets are 0.5 m/s. The time step is set as 0.001 s.

The result of the LCDM with △t=0.00001 s is considered as the "exact solution", which is used to be compared with the solutions of other methods. The displacements of the CEMDTS, the Newmark method, the generalized-a method (GaM) and the precise integration method (PIM) are shown in Fig. 9. It is obvious that the CEMDTS possesses the highest accuracy in the four algorithms. The error of the PIM is great than that of the CEMDTS. However, the tendency of the results of the PIM accords with the exact solution. The results of the Newmark method and the GaM are thoroughly different from the exact solution.

Fig. 9 Displacement of a wheel set (△t=0.001 s)

6 Discussion

The CEMDTS and the leapfrog central difference method belong to the acceleration method. The integration schemes do not have to be changed when they are implemented in nonlinear systems. Increment formats or predictor-corrector formats are generally employed in the implicit method and the displacement method in nonlinear systems. The increment formats are applied to the Newmark method and the generalized-a method. The predictor-corrector formats are employed in the precise integration method. The precise integration method is endowed with high accuracy in linear systems. Moreover, if a prediction method of high accuracy such as the Lagrange’s interpolation is used, its accuracy can also be very high in nonlinear systems. Meanwhile, the computation effort will increase rapidly. However, if the time step or the end time is long enough, the accumulative error of the precise integration method will increase constantly and result in numerical divergence finally.

The dynamic degree of nonlinearity with the maximum absolute value is -1.01 and 2 in the example of the pendulum. The maximum degree of nonlinearity is 68.5 and 1.09 in example 2 and the building example. The degree of nonlinearity is infinitely great for the vehicle example. It is obvious that the building example belongs to a weak nonlinear problem, and the vehicle example is a strong nonlinear one.

The phase loci of the nonlinear pendulum solved by the Newmark method and the generalized-a method are snake-like in example 1 under the initial condition 1. The main reason is that a negative stiffness area exists in the interval of [0.5p, 0.95p], and the oscillation and divergence will happen when the numerical errors accumulate to a certain degree. If the time step or the end time is increased, the phase locus of the snake-like shape will also occur in the precise integration method, which is similar to that of the Newmark method. The divergent results are shown in Figs. 10 and 11. Similarly, the theoretical value of the maximum angular displacement is 0.33p under the initial condition 2. As long as the end time is long enough, the phase locus of the Newmark method will be snake-like when the angular displacement exceeds p due to the increasing accumulative error.

Fig. 10 Phase locus of pendulum for precise integration method (t_end=1800 s)

Fig. 11 Phase locus of pendulum with a large time step (△t= 0.8 s)

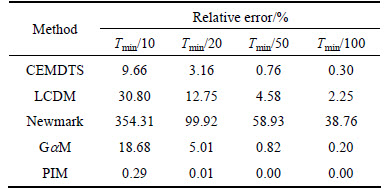
In example 2, the result of the Newmark method is stable, but the phase locus continues to decay. As a result, the energy of the numerical results of the Newmark method is not conserved. However, the error of the phase loci of other four methods is quite small because the time step is only 1/76 of the minimum natural period. We investigate the influence of the time step on the algorithm accuracy. The maximum relative errors of energy are listed in Table 1 under the condition of different time steps. The decreasing order of the algorithm accuracy is the precise integration method (PIM), the CEMDTS, the generalized-a method (GaM), the LCDM and the Newmark method. The accuracy of the precise integration method, the CEMDTS and the generalized-a method satisfies engineering requirements with the time step △t≤T_min/20.

Table 1 Maximum relative error of energy for various methods

In the building example, the accuracy of the precise integration method is the highest, and its computation effort is also the largest. Moreover, its stable interval is smaller than that of other methods. The computation effort of the Newmark method is almost equal to that of the CEMDTS because there are only 7 DOFs in this system. However, if the number of DOF increases, the superiority of the computational efficiency of the CEMDTS will be conspicuous. However, the CEMDTS is more accurate than the precise integration method in the vehicle example. The reason is that the degree of nonlinearity is different in the two examples, and the CEMDTS is more applicable than other methods in strong nonlinear systems.

In summary, the implicit integration method is not unconditionally stable in nonlinear systems. The displacement method possesses poor stability in nonlinear systems due to the effect of time step and the end time. The CEMDTS and the leapfrog central difference method are suitable for the nonlinear systems, and the results are highly consistent with the exact solution. Moreover, the accuracy of the former is higher than that of the latter.

7 Conclusions

1) The precise integration method, the Newmark method and the generalized-a method are conditionally stable in nonlinear systems. The stable interval of the three methods is less than that of the CEMDTS.

2) The accuracy of the precise integration method will be the highest when the time step satisfies △t≤T_min/20. Meanwhile, the CEMDTS possesses the smallest computation effort which is less than that of the precise integration method obviously. The accuracy of the CEMDTS is the highest if the time step is large (△t≥0.3T_min) or the system is strong nonlinear. The smaller the time step is, the higher the accuracy and the computation effort are.

3) The time step △t=T_min/20 is recommended for nonlinear systems. The accuracy of the CEMDTS and the precise integration method can meet the engineering requirements under this condition. Moreover, the computation effort of the CEMSTS is the smallest. Consequently, the CEMDTS is more applicable to the nonlinear vibration systems.

References

[1] ZHAI W M, GAO J, LIU P, WANG K. Reducing rail side wear on heavy-haul railway curves based on wheel–rail dynamic interaction [J]. Vehicle System Dynamics, 2014, 52(s): 440-454.

[2] ZHAI W M, WANG K Y, CAI C B. Fundamentals of vehicle-track coupled dynamics [J]. Vehicle System Dynamics, 2009, 47(11): 1349-1376.

[3] ZHAI Wan-ming, XIA He. Train-track-bridge dynamic interaction: Theory and engineering application [M]. Beijing: Science Press, 2011. (in Chinese)

[4] HILBER H M, HUGHES T J R, TAYLOR R L. Improved numerical dissipation for time integration algorithms in structural dynamics [J]. Earthquake Engineering and Structural Dynamics, 1977, 5: 283-292.

[5] CHUNG J, HULBERT G M. A time integration algorithm for structural dynamics with improved numerical dissipation: the generalized-a method [J]. Journal of Applied Mechanics, 1993, 60(2): 371-375.

[6] WEN W, JIAN K, LUO S. An explicit time integration method for structural dynamics using septuple B-spline functions [J]. International Journal for Numerical Methods in Engineering, 2014, 97(9): 629-657.

[7] XIE Y M. An assessment of time integration schemes for non-linear dynamic equations [J]. Journal of Sound and Vibration, 1996, 192(1): 321-331.

[8] ZHONG W X, WILLIAMS F W. A precise time step integration method [J]. Proc IMechE, Part C: Journal of Mechanical Engineering Science, 1994, 208: 427-430.

[9] ZHONG Wan-xie. On precise time integration method for structural dynamics [J]. Journal of Dalian University of Technology, 1994, 34(2): 131-135. (in Chinese)

[10] CHEN R L, ZENG Q Y, ZHANG J Y. New algorithm applied to vibration equations of time-varying systems [J]. Journal of Central South University of Technology, 2008, 15(s1): 57-60.

[11] CHANG S Y. An explicit method with improved stability property [J]. International Journal for Numerical Methods in Engineering, 2009, 77(8): 1100-1120.

[12] CHANG S Y. A family of noniterative integration methods with desired numerical dissipation [J]. International Journal for Numerical Methods in Engineering, 2014, 100(1): 62-86.

[13] MASURI S U, HOITINK A, ZHOU X, TAMMA K K. Algorithms by design: A new normalized time-weighted residual methodology and design of a family of energy–momentum conserving algorithms for non-linear structural dynamics [J]. International Journal for Numerical Methods in Engineering, 2009, 79: 1094-1146.

[14] YANG C, XIAO S, LU L, ZHU T. Two dynamic explicit methods based on double time steps [J]. Proc IMechE, Part K: Journal of Multi-body Dynamics, 2014, 228(3): 330-337.

[15] ZHANG Xiong, WANG Tian-shu. Computational dynamics [M]. Beijing: Tsinghua University Press, 2007: 147-184. (in Chinese)

[16] LEONTIEV V A. Extension of LMS formulations for L-stable optimal integration methods with U0-V0 overshoot properties in structural dynamics: The level-symmetric (LS) integration methods [J]. International Journal for Numerical Methods in Engineering, 2007, 71: 1598-1632.

[17] SHAO Hui-ping, CAI Cheng-wen. A three parameters algorithm for numerical integration of structural dynamic equations [J]. Chinese Journal of Applied Mechanics, 1988, 5(4): 76-82. (in Chinese)

[18] LU He-xiang, YU Hong-jie, QIU Chun-hang. An integral equation of nonlinear dynamics and its solution method [J]. Acta Mechanica Solida Sinica, 2001, 22(3): 303-308. (in Chinese)

[19] CHANG S Y. A new family of explicit methods for linear structural dynamics [J]. Computers & Structures, 2010, 88(11, 12): 755-772.

[20] YANG Chao, XIAO Shou-ne, YANG Guang-wu, ZHU Tao, YANG Bing. Non-dissipative explicit time integration methods of the same class [J]. Journal of Vibration Engineering, 2015, 28(3): 441-448. (in Chinese)

(Edited by YANG Bing)

Cite this article as: YANG Chao, YANG Bao-zhu, ZHU Tao, Xiao Shou-ne. Comparison and assessment of time integration algorithms for nonlinear vibration systems [J]. Journal of Central South University, 2017, 24(5): 1090-1097. DOI: 10.1007/s11771-017-3512-y.

Foundation item: Projects(51405402, 51505390) supported by the National Natural Science Foundation of China; Projects(2016YFB1200404, 2016YFB1200505) supported by the National Key Research and Development Program of China

Received date: 2015-09-02; Accepted date: 2016-03-08

Corresponding author: ZHU Tao, PhD; Tel: +86-28-86466433; E-mail: zhutao034@swjtu.cn