Trans. Nonferrous Met. Soc. China 23(2013) 773-780
Grain refinement of Mg-Al alloys by optimization of process parameters based on three-dimensional finite element modeling of roll casting
Hong-jun HU1,2
1. College of Materials Science and Engineering, Chongqing University of Technology, Chongqing 400050, China;
2. Key Laboratory of Manufactured and Test Techniques for Automobile Parts of Ministry of Education, Chongqing University of Technology, Chongqing 400050, China
Received 31 October 2011; accepted 16 February 2012
Abstract: To study the influence of roll casting process parameters on temperature and thermal-stress fields for the AZ31 magnesium alloy sheets, three-dimensional geometric and 3D finite element models for roll casting were established based on the symmetry of roll casting by ANSYS software. Meshing method and smart-sizing algorithm were used to divide finite element mesh in ANSYS software. A series of researches on the temperature and stress distributions during solidification process with different process parameters were done by 3D finite element method. The temperatures of both the liquid-solid two-phase zone and liquid phase zone were elevated with increasing pouring temperature. With the heat transfer coefficient increasing, the two-phase region for liquid-solid becomes smaller. With the pouring temperature increasing and the increase of casting speed, the length of two-phase zone rises. The optimized of process parameters (casting speed 2 m/min, pouring temperature 640 °C and heat transfer coefficient 15 kW/(m2·°C) with the water pouring at roller exit was used to produce magnesium alloy AZ31 sheet, and equiaxed grains with the average grain size of 50 μm were achieved after roll casting. The simulation results give better understanding of the temperature variation in phase transformation zone and the formation mechanism of hot cracks in plates during roll casting and help to design the optimized process parameters of roll casting for Mg alloy.
Key words: magnesium alloy; roll casting; process parameter; 3D finite element method; thermal-stress
1 Introduction
In recent years, an improvement of energy efficiency in the magnesium processing industry has been achieved due to the application of roll-casting technology. The main advantages of magnesium alloy are that it is 36% lighter per unit volume than aluminum and 78% lighter than iron. Magnesium alloys have benefits of high specific strength and stiffness and excellent machinability, castability and shielding capability against electromagnetic interference [1]. The cast magnesium alloy sheets are hot-rolled at an elevated temperature. The roll casting process has been widely used in the magnesium industry for the production of plates for several decades due to its higher productivity and improved cast surface quality. Unfortunately, the process may produce defects in the plates, for magnesium plates are suffered uneven cooling rates in different regions. The cracks are due to an opening of the mushy zone where the dendrite arms can be separated easily. The microstructure changes in different parts of the plates are due to the different cooling rates. It is important to research the cracking tendency during roll casting. A number of numerical studies have been conducted to simulate the casting process under various operating conditions [2]. Finite element method (FEM) is the most commonly used numerical technique for the problems of transient heat conduction. HU et al [3] researched distribution of temperature and flow fields in cast-rolling zone through the heat flow coupling solution using finite element method. But the thermal stress which could cause cracks of plates has not been studied. Although the investigations of roll-casting processes for magnesium alloy have been done by many researchers, the quantitative relationships among process parameters have not been explored carefully.
In this work, three-dimensional 3D FEM thermal analyses on the solidification region were performed using finite element analysis of ANSYS software. This is intended to obtain stress and temperature distributions with the usage of commercial finite-element software ANSYS. The development of a fully coupled 3D thermal stress model for plates of AZ31 (with about 3% Al) was described during the solidification of the roll casting process. The temperature field and thermal stress calculation results were analyzed and compared with different process parameters including pouring temperatures, heat transfer coefficients, casting speeds and water poured at roller export or not, etc. The characteristics of the thermal stress and temperature distributions with different conditions during roll casting process were described. Experiments were done by a roll casting roller with optimization parameters. The microstructures of the as-cast wrought alloy sheets were observed to investigate the effects of the casting process conditions on crystal growth in the cast products.
2 Description of physical and mathematical models
2.1 Basic assumptions for roll casting of magnesium alloy
The roll casting process consists of two water-cooled rollers which are driven and oppositely rotating independently. Figure 1 shows a schematic diagram for roll casting of magnesium alloy, which is a half model of casting zone and top roller. The simulations are set up in metric unit and in rectangular cartesian coordinate system. In the process, molten metal flew through the nozzle casting zone, with strong heat transfer taking place [4,5]. The temperature and stress fields of the process are complex, which involve the fluid mechanics, heat transfer, calculation method, mathematical theory of partial differential equations and the theories of casting process. In order to simplify the calculations of temperature and thermal stress field, the simplification and assumptions are as follows [6]. The sheet width (1 m to 1.5 m) is much larger than the length of casting area and the sheet thickness, so the width direction of heat transfer is ignored. Molten metal of AZ31 magnesium alloy releases latent heat during solidification. Latent solidification heat releases even in the solidification temperature range. Some properties vary with temperature. The values of conductivity and specific heat and other properties are independent on the space and time. Roller diameter is much larger than the length of casting zone. It is assumed that the contact interface between roller and the sheet is a straight line and the arc of contact zone is ignored. Solid-phase region contacts with the roll surface closely, and the roll is not deformed. The contract stress and gap between plate and rollers are omitted.
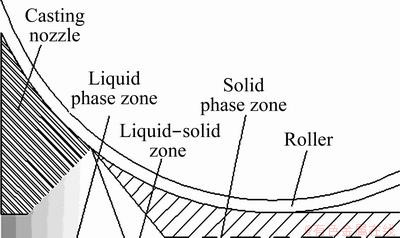
Fig. 1 Model schematic representation of roll casting process
2.2 Roll casting process parameters and 3D finite element model
Main structural parameters of roller and casting process conditions are shown in Table 1. Geometric models are established and thermal-structural coupled asymmetric unit PLANE13 and Solid5 in ANSYS software have been selected. Half of geometric models were studied along the sheet center because the upper and lower rolling structures are symmetrical. Free mesh method to determine the shape of the grid and smart-sizing algorithm to determine the unit size are applied. Geometric model and the results of finite element mesh are shown in Fig. 2.
Table 1 Main parameters of roller and roll casting conditions
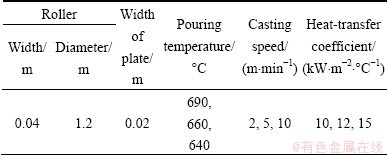

Fig. 2 Geometry model and FEM meshing
2.3 Calculation equation for temperature and thermal stress field
Differential equation for temperature field calculation is as follows [7-9]:
 (1)
(1)
where ρ is density, c(T) is the specific heat capacity varying with temperature, T is the temperature, τ is casting time, and λ(T) is the thermal conductivity.
The method of disposing the phase latent heat during the course of magnesium solidification is equivalent specific heat capacity, the phase latent heat is released which raises the liquid temperature. The method of equivalent specific heat capacity is considered. The value of phase latent heat is taken as one part of the equivalent specific heat capacity [10], which can be expressed by
 (2)
(2)
where ce, cL and L represent equivalent specific heat capacity, the specific heat capacity of magnesium alloy, latent heat of solidification, respectively; TL and TS are the temperatures of liquidus and solidus curves, respectively.
The deformation and stress–strain of roll cast plates in casting zone can be obtained from the thermal elastic–plastic boundary conditions based on the small deformation theory. The mathematical model of thermal stress can predict the strain and stress distribution in the casting zone which provides an very important information about the plate quality, especially the crack formation. The stress–strain evolution problem is governed by Eq. (3). The von Mises yield criterion is determined by the yield stress and the hardened modulus. The total incremental strain {ε} is as follows:
{ε}={εel}+{εpl}+{εth} (3)
where {εel}, {εpl}, and {εth}are the incremental elastic strain component, plastic strain component, and thermal strain component, respectively. The relationship between incremental elastic strain and stress is linear relation and can be written as follows:
dσ=D(εel+εpl+εth) (4)
where D is the elasticity matrix.
The thermally induced strain and stress are calculated on the basis of the calculated temperature distribution and the thermal coefficient of the materials. The relationship between the thermally induced strain and stress is determined by using an elasto-viscoplastic material constitutive model. The stress is calculated using the roll-casting model, and the strength is measured from high-temperature mechanical property data [9,10].
2.4 Boundary conditions and physical parameters of AZ31
Symmetric center plane is regarded as adiabatic boundary. The equation of heat transfer for the contact interface between plate and roller is expressed as
 (5)
(5)
where λ(T) is the thermal conductivity, h(T) is the heat transfer coefficient between the melts and roller, Ts is temperature of plate surface and Tfis the temperature of the roller. The casting temperature is initialized by T|τ=0=Tpour, where Tpour is the pouring temperature. The initial temperatures of roller and water are regarded as the same of 25 °C.
Simulation for roll casting process involves the physical properties such as the material density, specific heat capacity, and thermal conductivity. The density of AZ31 magnesium alloy is 1780 kg/m3. Thermal conductivity and effective specific heat for AZ31 magnesium alloy at different temperatures are shown in Table 2 and Table 3, respectively.
Table 2 Heat conductive coefficients of AZ31 magnesium alloy under different temperatures [11]

Table 3 Effective specific heat capacity of AZ31 magnesium alloy under different temperatures [12]

3 Results and discussion
The initial temperatures of pouring temperature are 690, 660 and 640 °C, respectively. Heat transfer coefficients between roller and plate are 10, 12 and 15 kW/(m2·°C) respectively. Casting speeds are 2, 5 and 10 m/min, respectively. The effects of process parameters (the casting speeds and the pouring temperature, heat transfer coefficient of roll/plate contact interface) on temperature field and thermal stress distribution in the plate were studied.
3.1 Influence of pouring temperature on temperature and thermal stress distribution in plates
When the casting speed is 10 m/min, heat transfer coefficient between roller and plate is 10 kW/(m2·°C), and pouring temperature is changed from 640 °C and 660 °C to 690 °C, other process parameters remain the same. The simulation results are shown in Fig. 3. It can be seen that temperature of plate exit becomes higher with the pouring temperature increasing. When the pouring temperature increases from 640 °C to 690 °C, the temperature of plate surface rises from 413 to 452 °C. It can be seen from Figs. 3(a)-(c), temperature decreases gradually from the entrance to the roller exit. From surface of plate to the center, the temperature increases gradually. The length of the solidification region becomes longer with the pouring temperature rising. If roller exit is cooled by water when pouring temperature is 640 °C, the temperature of front plate will drop and temperature uniformity increases obviously from Figs. 3(a) and (d), and the cooling at the roller exit may not influence the temperature in liquid region. Figure 4 shows the distributions of thermal stress with heat-transfer coefficients 10 kW/(m2×°C) and casting speed 10 m/min and water pouring at the roller exit or not when the pouring temperature is 640 °C. It is found that the thermal stress will be reduced considerably if water is poured at the roller exit.
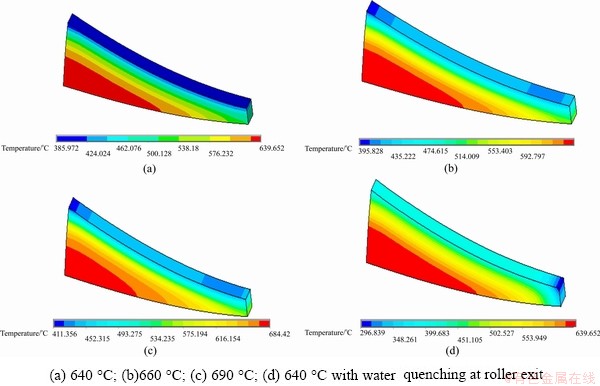
Fig. 3 Temperature field distribution under different pouring temperatures
From the above simulation results, it can be drawn that lower pouring temperature could reduce the thermal stress in the plate if the liquidity of AZ31 is enough.
3.2 Influence of heat transfer coefficient on temperature and thermal stress in the plate
To study the influence of coefficients at roll/plate
interfaces on the temperature distribution in the plate, heat transfer coefficients at roll/plate contact interfaces are set to be 12 and 15 kW/(m2·°C). The pouring temperature is 640 °C and the casting speed is 10 m/min.

Fig. 4 Distributions of thermal stress with heat-transfer coefficient 10 kW/(m2·°C) and casting speed 10 m/min
Simulation results are shown in Fig. 5. It can be seen from Fig. 3(a) and Fig. 5(b) that temperature at the roller exit decreases with the heat transfer coefficient increasing if other process parameters remain unchanged. When the heat transfer coefficient is 10 kW/(m2·°C), the temperature of plate at roller exit is about 462 °C. When heat transfer coefficient increases to 12 kW/(m2·°C), the temperature of plate outlet drops to 441 °C. If the interface heat transfer coefficient jumps to 15 kW/(m2·°C), the temperature for plate at roller exit reduces to 414 °C.

Fig. 5 Temperature field with different heat transfer coefficients
It can be found from Fig. 6 that the thermal stress of plate surface at roller exit reduces with heat transfer coefficient increasing. When the heat transfer coefficient increase to 15 kW/(m2·°C), thermal stress significantly reduces. Figure 7 shows the simulation results when the heat transfer coefficient is 15 kW/(m2·°C) and casting speeds is 10 m/min, thermal stress at roller exit is about 4433 Pa.
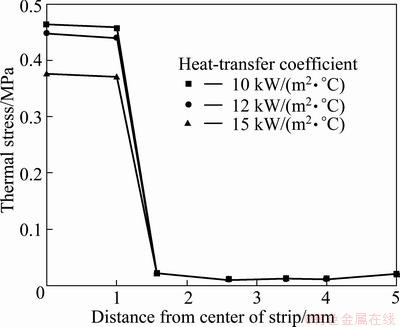
Fig. 6 Distributions of thermal stress at different pouring temperatures and heat-transfer coefficients at roller exit

Fig. 7 Distribution of thermal stress with heat-transfer coefficient of 15 kW/(m2·°C)
From the above simulation results it is concluded that a larger heat transfer coefficient should be chosen and the water-cooled strength ought to be increased, and the cooling intensity only can be enhanced. These measures can lower the temperature and thermal stress of plates at the roller exit, and reduce heat cracks. These results are in agreement with the results in Refs. [12-18].

Fig. 8 Temperature field distribution under different casting speeds
3.3 Influence of casting speed on temperature and thermal stress
There is a closer relationship between thermal stress distributions and the casting speed in casting zone. To study the changes of casting speed and its influence on temperature field, simulation conditions are set. Pouring temperature is 640 °C, heat transfer coefficient is 10 kW/(m2·°C), and casting speeds are 2, 5 and 10 m/min, respectively. The simulation results are shown in Fig. 3(a) and Fig. 8, which show that if the other conditions remain unchanged, with the increase of casting speed, temperature of plate at roller exit increases. When the casting speed is improved from 2 to 10 m/min (see Fig. 3(a)), temperature at the roller exit increases from 273 to 387 °C, and thermal stress rises from 1792 to 2917 Pa.
From the above analyses it is shown that if the pouring temperature of the AZ31 magnesium alloy is high, the casting speed will be reduced. If the pouring temperature is low, the casting speed improves and the flow rate of magnesium increases to prevent premature solidification. The simulations results are in agreement with results in Refs. [13,14] which include the influence of casting speed on temperature field.
3.4 Way to avoid crack defects during roll casting
To avoid the defects in the plates, some measures should be taken [15-17]. Cooling velocity of water ought to be increased to raise the heat-transfer coefficient between the plates and roller. In this work, the 15 kW/(m2·°C) is selected, but in actual production the value can be improved as large as possible. The pouring temperature should be reasonable, here 640 °C is chosen. The roll casting process ought to satisfy the following conditions: ην=C, where η is slag viscosity, v is casting speed and C is constant, the casting speed is equal to 2 m/min.
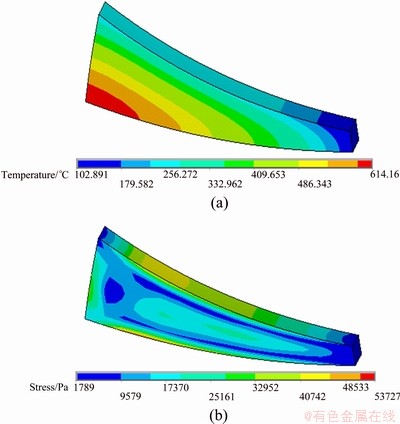
Fig. 9 Distributions of temperature (a) and thermal stress (b) with heat-transfer coefficient 15 kW/(m2·°C) and casting speed 2 m/min (Cooling water is poured at the roller exit)
If the new simulation conditions are set up (casting speed 2 m/min, heat-transfer coefficient 15 kW/(m2·°C-1), pouring temperature 640 °C), the boundary conditions are different from the former simulation conditions and the cooling water with temperature 25 °C would be poured at the roller exit. The results of temperature and thermal-stress are shown in Fig. 9. By comparison with Fig. 3(a) and Fig. 9, it can be seen that the lowest temperature of the plate at roller exit decreases from 386 to 102 °C, the thermal stress drops from 4433 Pa to 1789 Pa. So cooling the plate at the roller exit could reduce the tendency of cracks caused by thermal stress.
4 Experimental verification
Experiments have been done by rapid roll casting. The main process parameters are as follows: casting speed of 2 m/min and pouring temperature of 640 °C. The cooling water with temperature 25 °C is poured at the roller exit. A laboratory scale test procedure is defined to evaluate the evolution of the grain size distribution after rolling casting of AZ31 alloy provided in standard industrial as-cast conditions (Mg-3%Al- 1%Zn). Figure 10 shows the microstructures of cast AZ31 plates obtained by rapid roll casting at speed of 8 m/min and pouring temperature of 640 °C. It can be seen that microstructures of the cast plate are almost entirely equiaxed, and the grain sizes of equiaxed grains are from 10 to 50 μm on the plate surface. Sizes of grains are coarser in the center than on surface and up to 100 μm. Equiaxed grains with the average grain size 50 μm are achieved after casting if the plates are cooled at the roller exit. The experimental results are accorded with the description of the roll casting parameters which influence the microstructures [18].
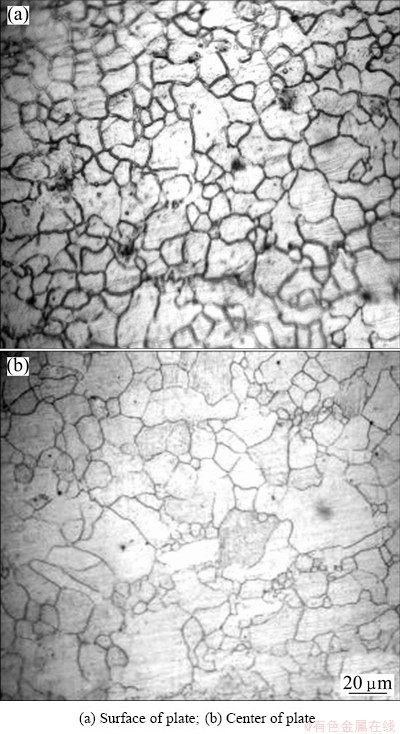
Fig. 10 Microstructures of cast AZ31plate at casting speed of 2 m/min and pouring temperature of 640 °C
5 Conclusions
1) With the increase of casting speed, two-phase region for liquid-solid increases, the length of casting liquid region, increases too. Temperature of plate surface, end point position for solidification near the roller exit and thermal stress of plate increase, but thickness of solidification shell becomes smaller.
2) The temperatures of liquid-solid phase region and liquid region are elevated, which will cause thermal stress rising with the pouring temperature increasing. Lower pouring temperature with water pouring at roller exit can reduce the temperature and thermal stress in the as-cast plate.
3) With the heat transfer coefficient increasing, the two-phase region for liquid-solid becomes smaller, the length of the liquid region decreases slightly and solidified shell becomes thick.
4) The 3D simulation results show that the process parameters of roll casting process for magnesium alloy are interacted. Some measures to avoid the crack defects during roll casting are put forward. The optimization of process parameters was used to produce as-cast plate with cooling water pouring at the roller exit. Equiaxed grains with the grain size of about 50 μm are achieved.
References
[1] GONG X, LI H, KANG S B, CHO J H, LI S. Microstructure and mechanical properties of twin-roll cast Mg-4.5Al-1.0Zn alloy sheets processed by differential speed rolling [J]. Materials and Design, 2010, 31(3): 1581-1587.
[2] YOU B S, YIM C D, KIM S H. Solidification of AZ31 magnesium alloy plate in a horizontal continuous casting process [J]. Materials Science and Engineering A, 2005, 413–414: 139–143.
[3] HU Zhao, LI Pei-jie, HE Liang-ju. Coupled analysis of temperature and flow during twin-roll casting of magnesium alloy strip [J]. Journal of Materials Processing Technology, 2011, 211: 1197-1202.
[4] HU Xiao-dong, JU Dong-ying. Application of Anand’s constitutive model on twin roll casting process of AZ31 magnesium alloy [J]. Transactions of Nonferrous Metals Society of China, 2006, 16: 586-590.
[5] ZHANG L. Numerical simulation on solidification and thermal stress of solid shell in continuous casting crystallizer based on meshless method [D]. Beijing: Tsinghua University, 2004. (in Chinese)
[6] GUO Peng, ZHANG Xing-guo, HAO Hai. Temperature simulation of direct chill casting of AZ31 magnesium alloy billets [J]. The Chinese Journal of Nonferrous Metals, 2006, 16: 570-1577. (in Chinese)
[7] HU Hong-jun, ZHANG Ding-fei, YANG Ming-bo, DENG Ming. Grain refinement in AZ31 magnesium alloy rod fabricated by an ES SPD process [J]. Transactions of Nonferrous Metals Society of China, 2011, 21(2): 243-249.
[8] HAO H, AIJER D M, ELLS M A. Development and validation of a thermal model of the direct chill casting of AZ31 magnesium billets [J]. Metallurgical and Materials Tractions A, 2004, 35: 3843-3854.
[9] HAN I Q, HASSAN M I, VISWANATHAN S. The reheating-cooling method: A technique for measuring mechanical properties in the nonequilibrium mushy zones of alloys [J]. Metallurgical and Materials Tractions A, 2005, 36: 2073-2080.
[10] GUO Shi-jie, CUI Jian-zhong, LE Qi-chi. The effect of alternating magnetic field on the process of semi-continuous casting for AZ91 billets [J]. Mater Lett, 2005, 59: 1841-1844.
[11] PAN Fu-sheng, ZHANG Jing, WANG Jing-feng, YANG Ming-bo, HAN En-hou, CHEN Rong-shi. Key R&D activities for development of new types of wrought magnesium alloys in China [J]. Transactions of Nonferrous Metals Society of China, 2010, 20(7): 1249-1258.
[12] JIAO Ji-cheng, ZHAO Chuan-ling, SHAO Wei. Study on modeling and simulation at No.3 continuous caster in jigging [J]. Journal of System Simulation, 2007, 19: 5482-5486.
[13] GUO Zhen-yu, AN Qiang, CHENG Bo. Research on work roll temperature with improved differential evolution in hot strip rolling process [J]. Journal of System Simulation, 2007, 19: 4877-4880.
[14] GONG X, KANG S B, LI S, CHO J H. Enhanced plasticity of twin-roll Cast ZK60 magnesium alloy through differential speed rolling [J]. Materials and Design, 2009, 30(9): 3345-3350.
[15] HU Xiao-dong, JU Dong-ying. Application of Anand’s constitutive model on twin roll casting process of AZ31 magnesium alloy [J]. Transactions of Nonferrous Metals Society of China, 2006, 16: 586-590.
[16] CHATTERJEE D, CHAKRABORTY S. An enthalpy-source based lattice Boltzmann model for conduction dominated phase change of pure substances [J]. International Journal of Thermal Sciences, 2008, 47: 552-559.
[17] HU Hong-jun, ZHANG Ding-fei, ZHANG Jun-ping. Microstructures in an AZ31 magnesium alloy rod fabricated by a new SPD process based on physical simulator [J]. Transactions of Nonferrous Metals Society of China, 2010, 10(3): 478-483.
[18] PAN Fu-sheng, HAN En-hou. High performance magnesium alloys and processing technology [M]. Beijing: Chemical Industry Press, 2005. (in Chinese).
基于三维有限元铸轧工艺模拟及工艺参数优化的Mg-Al合金晶粒细化
胡红军1,2
1. 重庆理工大学 材料科学与工程学院,重庆 400050;
2. 重庆理工大学 汽车零部件制造及检测技术教育部重点实验室,重庆 400050
摘 要:为了获得质量优异的镁合金薄板材并研究铸轧工艺参数对AZ31镁合金薄板材的温度场和热应力场的影响,基于铸轧的对称性采用ANSYS软件建立了三维几何和有限元模型。在ANSYS软件中采用smart-sizing算法进行网格划分。进行了一系列不同工艺参数下的三维温度场和热应力数值模拟。结果表明,随着浇注温度的升高,液相区和液固两相区的长度都增加;随着辊/薄板间接触的对流换热系数的增大,液固两相区的长度减小;随着浇注温度和铸轧速度的提高,两相区的长度增大。将优化的工艺参数(铸造速度2 m/min、浇注温度 640 °C、换热系数15 kW/(m2·°C)及水淬)用于镁合金铸轧试验,得到平均晶粒尺寸为50 μm的镁合金板坯。三维仿真结果能更好地理解相变区的温度变化和铸轧过程中热裂纹的形成机理,为设计和优化镁合金铸轧的工艺参数提供帮助。
关键词:镁合金;铸轧;工艺参数;三维有限元法;热应力
(Edited by Xiang-qun LI)
Foundation item: Project (CSTC 2010BB4301) supported by Natural Science Foundation Project of Chongqing, China; Project supported by the Open Fund for Key Laboratory of Manufacture and Test Techniques for Automobile Parts of Ministry of Education Chongqing University of Technology, 2003, China
Corresponding author: Hong-jun HU; Tel/Fax: +86-23-68851783; E-mail: hhj@cqut.edu.cn
DOI: 10.1016/S1003-6326(13)62528-5