文章编号：1004-0609(2016)-09-2007-08

铝电解槽阴极钠扩散及热应力-钠膨胀耦合的计算

王  恒¹，周凯琦¹，周终强²，黄  俊²

(1. 华中科技大学 力学系，武汉 430074；

2. 贵阳铝镁设计研究院有限公司，贵阳 550081)

摘  要：利用ANSYS Workbench仿真平台建立铝电解槽热应力-钠膨胀耦合计算的有限元模型，提出利用非稳态质量扩散和瞬态热传导的相似性模拟钠扩散的方法，得到了钠在阴极炭块中的浓度分布。根据钠浓度的分布将钠膨胀系数转化为热膨胀系数，实现钠膨胀和热膨胀的间接耦合，模型还考虑钢的塑性变形和摩擦接触，计算结果与实际情况吻合较好。

关键词：铝电解槽；钠扩散；热应力；钠膨胀；有限元

中图分类号：TF821　　     文献标志码：A

电解槽是生产铝的主要装备之一。在生产过程中电解槽受力情况十分复杂，槽壳和摇篮架不仅要承受内衬的热膨胀和钠膨胀还要承受上部结构的压力以及自身质量，有时槽壳和摇篮架会因受力过大而屈服，导致电解槽损坏。此外，阴极的破损也是电解槽停槽的主要原因之一。在铝电解过程中，除了铝的析出外还会有钠的析出，钠析出以后会向阴极炭块进行扩散，并和阴极炭块进行反应，导致阴极炭块体积膨胀产生钠膨胀应力。钠膨胀应力是阴极炭块破损的重要原因之一。目前大多数学者主要通过做实验来对钠扩散和钠膨胀进行研究^[1-2]，数值模拟的结果还很少。本文作者提出利用非稳态质量扩散和瞬态热传导的相似性模拟钠扩散的方法，对钠浓度的分布进行了模拟，并把钠膨胀转化为热膨胀系数，计算热膨胀和钠膨胀对电解槽的耦合作用。

电解槽应力场的研究对于优化电解槽结构、延长寿命具有重要意义，目前的研究重点主要集中在槽壳和阴极炭块应力上^[3]，计算时把槽壳、摇篮架或阴极炭块单独建模进行计算，本文作者对电解槽进行综合考虑，在1/4整槽模型中对电解槽应力场进行计算。

对电解槽应力场的有限元仿真有许多困难：许多保温内衬的力学性能难以确定；电解槽结构和外形十分复杂，难以得到高质量的网格；槽壳和摇篮架等钢材具有塑性，如不考虑塑性变形，则计算出来的应力容易出现异常；模型本身有许多地方需要设置为摩擦接触，而摩擦接触的计算高度非线性，很容易不收敛。本文作者利用ANSYS Workbench中的Static Structural模块对电解槽的受力状况进行研究，在研究中划分较高质量的网格，考虑钢材的塑性变形和摩擦接触，并且经过多次迭代得到了收敛的结果。

1  计算模型和方法

1.1  钠膨胀的计算模型与方法

钠膨胀不能直接施加到模型中，需要进行近似，本文作者把钠膨胀系数转化为热膨胀系数，把钠膨胀以材料属性的方式加进去^[4]。为此需要把阴极炭块分成10层，如图1所示。每一层炭块对应不同的钠浓度以及钠膨胀系数，把钠膨胀系数转化为热膨胀系数以后，给每一层炭块赋予不同的等效热膨胀系数，这样在热应力计算中就可以把钠膨胀考虑进去。计算流程如图2所示。

1.2  电热场计算

1.2.1  几何模型

本文作者利用三维建模软件Solid works建立了电解槽全槽模型，模型包括母线部分、阳极部分、电解质、铝液、阴极部分、保温内衬、槽壳和摇篮架。其中阳极炭块高度根据换极表进行确定，与实际情况更加接近。几何模型如图3所示。

电解槽主要结构参数如表1所列。

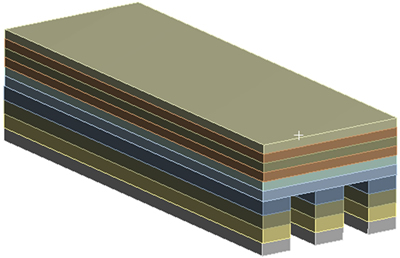
图1  阴极炭块分层

Fig. 1  Slice of cathode carbon block

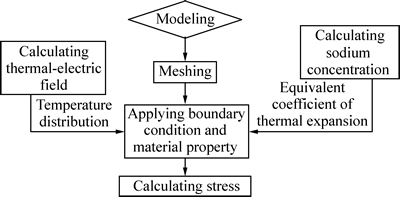
图2  耦合计算流程图

Fig. 2  Process of coupling calculation

图3  电热场计算几何模型

Fig. 3  Geometry model of thermo-electric field calculation

表1  电解槽主要结构参数

Table 1  Structural parameters of cell

1.2.2  数学模型

电场控制方程为^[5]

    (1)

式中：ρ_x、ρ_y、ρ_z为材料三维各个方向的电阻率，与温度相关；V是电位；τ是时间。

热场控制方程^[6]为

     (2)

式中：T为温度；k_x、k_y、k_z为三维各个方向的导热系数，与温度相关；q为由于电流通过单位体积产生的焦耳热，对于不导电的材料，q为0。

1.2.3  边界条件

电场边界条件为立柱母线底部施加总电流420 kA，阴极钢棒端头施加0电位。

热场边界条件为

1) 阳极底掌下面的电解质施加化学反应吸热条件^[7]，吸热量为2×10⁴ W/m³；

2) 覆盖料和钢爪等部位施加对流换热系数，换热系数由式(3)确定^[4]：

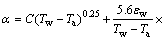
                 (3)

式中：第一项为强制对流换热系数，第二项为辐射换热系数；C为常数，T_w和T_a分别为换热面温度和外部环境温度，ε_w为表面黑度，钢爪、槽壳等部位为氧化后的钢，黑度取0.8。

3) 槽壳摇篮架等部位施加对流换热系数，换热系数由式(4)确定：

 (4)

式中：第一项为自然对流换热系数，第二项为辐射换热系数。

4) 环境温度由车间实测值给出。

5) 槽内熔体和槽帮之间是对流换热，电解质与槽帮表面的换热系数取600 W/(m²·K)，铝液与槽帮表面换热系数取800 W/(m²·K)^[8]。换热系数以接触热导率的方式施加。

1.2.4  材料属性

在生产过程中，电解槽整体的温度分布从几十度到1000度左右，所以施加的电阻率和热导率等材料属性需要随温度升高而变化。本研究中的材料属性从文献[4, 9]中获得。

2  钠扩散的计算

2.1  钠浓度计算方法

钠在阴极炭块中的扩散符合菲克扩散定律，非稳态扩散方程如式(5)所示^[10]：

                           (5)

式中：C为扩散物的体积浓度，kg/m³；t为时间，s；X为距离，m。

如果扩散系数D与浓度无关，则式(5)可以写成

                               (6)

瞬态热传导方程如式(7)所示：

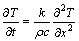                              (7)

式中：T为温度，K；t为时间，s；k为导热系数，W/(m·℃)；ρ为密度，kg/m³；c为比热容，J/(kg·℃)；X为距离，m。

在利用有限元方法求解微分方程时，通过把微分方程离散成等效的代数方程组来求解，并不涉及具体的物理量或单位。比较式(6)和式(7)可以看出，两个微分方程具有一致性，只是具体的量有所改变，因此，可以采用瞬态热传导方程的求解方法来求解非稳态扩散方程。两个方程各量之间的对应关系：热导方程中k/(ρc)和温度T分别对应扩散方程中的扩散系数D和体积浓度C。

根据以上对应关系来施加边界条件和材料属性即可在ANSYS中利用瞬态热场计算来等效钠扩散的计算，即设定边界时以温度代替浓度，并使材料属性满足式(8)：

                                (8)

式中：D为钠的扩散系数；k为炭块导热系数；ρ为密度；c为比热容。

2.2  边界条件及简化

1) 电解槽在焙烧启动初期钠的渗透比较剧烈^[11]，可以认为此时表层炭块已经达到饱和浓度。本文作者所采用半石墨质炭块饱和浓度为3%，所以炭块上表面钠浓度设为0.03，由于计算时用温度等效浓度，所以施加的边界为炭块上表面温度设为0.03 ℃。

2) 钠在阴极炭块中的扩散系数^[12]为4×10^-8 m²/s，为使式(8)成立，施加材料属性时根据式(8)来调整炭块的材料属性。炭块密度为1560 kg/m³，比热容为1672 J/(kg·℃)，根据式(8)传热系数调整为k=Dρc=0.1043 W/(m·℃)。

3) 计算时间设为一年。

2.3  钠浓度分布计算结果

图4所示为计算得到的温度分布，即等效的钠浓度分布，根据钠浓度的分布可以得到每一层炭块对应的钠膨胀率，进而转化成热膨胀系数。

图4  等效的钠浓度分布

Fig. 4  Distribution of sodium concentration

2.4  等效热膨胀系数的转化

不同的钠浓度对应不同的钠体膨胀率，如表2所列。

表2  不同钠浓度对应的钠膨胀率^[12]

Table 2  Sodium expansion coefficient of corresponding sodium concentration^[12]

钠膨胀转化为热膨胀系数可以分为以下几个步骤：

1) 2.3节中计算得到的是钠的分子浓度，表2中的浓度是质量浓度，因此，需要计算每层炭块的质量浓度。之后，可以得到每一层炭块对应的钠体膨胀率。

2) 热膨胀系数是线膨胀系数，体膨胀系数和线膨胀系数之间是3倍的关系，因此钠体膨胀率除以3可以得到相应的热膨胀率。

3) 以热膨胀率除以每层炭块的温度与室温的温差可以得到近似的热膨胀系数。

4) 由钠膨胀转化的热膨胀系数加上炭块自身的热膨胀系数即可得到等效的热膨胀系数。表3所列为各层炭块的温度和最终得到的等效热膨胀系数。

表3  等效热膨胀系数

Table 3  Equivalent coefficient of thermal expansion

3  热应力的计算

3.1  计算模型

热应力计算主要是要研究阴极炭块和槽壳摇篮架的变形，因此，可以从热场模型中去掉母线、阳极和熔体，在底部加上底部大梁和支柱得到。由于考虑了材料非线性和接触非线性，计算时间会比较长。考虑到模型本身具有对称性，为了节省计算时间采用1/4槽模型。热应力计算的有限元模型如图5所示。

图5  热应力计算有限元模型

Fig. 5  Finite element model of thermos-stress field calculation

3.2  材料属性

铝电解槽所使用的材料很多，大部分是保温材料，这些材料的导热性能参数比较容易得到，而力学性能很难得到详细的参数，本文作者所使用的材料参数参考一些文献[4，9]中给出的数值和一些测试结果^[13-14]。

电解槽在生产过程中一些区域应力水平会很高，如果不考虑钢的塑性变形，应力计算结果会很大^[15]，所以本文考虑了钢的塑性，具体材料属性如图5和表4所列。

表4  钢的材料属性

Table 4  Properties of steel

边界条件和载荷如下。

1) 底部支柱固定。

2) 整体施加重力加速度9.8 m/s²。

3) 阴极炭块上表面施加铝液和电解质压力6 kPa。

4) 小面槽沿板上施加上部结构压力，上部结构质量32 t。

5) 温度分布边界由电热场计算结果导入。

6) 接触设置： 摇篮架和槽壳之间的连接方式主要是焊接，其余部分是直接接触没有做任何处理，比如侧部大面槽壳和摇篮架垫块、底部摇篮架和槽壳，如图6(a)所示，这几处应设为摩擦接触。摇篮架是直接放在底部支撑梁上的，如图6(b)所示，所以也应设为摩擦接触。钢与钢之间的摩擦因数取0.15。

在实际生产过程中也可以观察到底部槽壳和摇篮架有脱离的现象，摇篮架和底部支撑梁也有脱离的现象。如果不设置摩擦接触的话相当于两个体强行贴合在一起，这会导致计算出来的应力与实际情况差别较大。

7) 对称面设置为Frictionless support 边界，Frictionless support 边界与对称边界是等效的。

3.3  计算结果及分析

本次计算的模型约有8万单元，51万节点。由于考虑材料非线性和接触非线性，模型计算一次耗时较长，约需12 h以上。经过多次迭代，最终可得到收敛的结果。

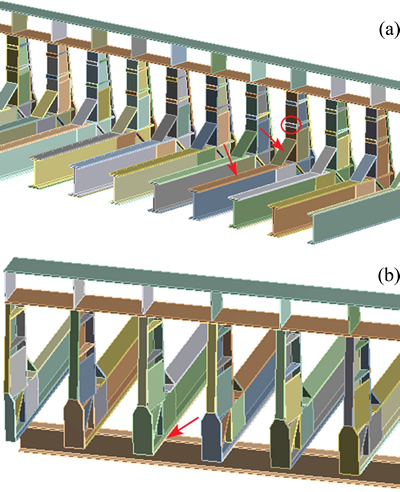
图6  摇篮架接触示意图

Fig. 6  Schematic diagram of contact of cradle rack

图7所示为电解槽的总位移分布和各方向位移分布，其中x方向是小面烟道端到出铝端，y方向是垂直大面并与进电方向一致，z方向是竖直方向。图7(a)是总位移分布云图，从图中可以看出最大位移为3 cm，出现在阴极炭块上表面。图7(b)是x方向位移分布云图，x方向最大位移为1.6 cm，出现在小面槽壳中部。图7(c)是y方向位移分布云图，y方向最大位移为2.6 cm，沿y轴负方向，出现在大面槽壳中部。图7(d)是z方向位移分布云图，z方向最大位移为3 cm，出现在阴极炭块上表面，可以看出阴极炭块整体有上拱的趋势。文献[16]给出了180 kA铝电解槽的位移测试结果，其测试结果显示y方向最大位移为1.85 cm，出现在槽壳大面中部，x方向最大位移为1.2 cm，出现在小面中部。测试结果与本文计算结果定性一致，但由于本研究对象为420 kA铝电解槽，槽型更大，因此，计算的位移比他们的测试结果稍大。

图8所示为槽壳摇篮架变形示意图。由图8可以明显看出，底部槽壳有上拱的趋势，底部槽壳与摇篮架已经脱开，底部槽壳中心处二者脱开的距离约为1 cm。这与实际生产中观察到的情况比较吻合。

图9所示为槽壳Mises应力和应变分布云图。由图9可以看出，槽壳应力集中处位于槽壳底部边缘，应力值达到322 MPa，其余大部分部位均低于216 MPa，槽壳最大应变为0.15%，远未达到屈服极限0.2%，因此，除应力最大部位需密切关注外，槽壳其它部位有一定的强度储备，比较安全。从应力和应变的分布可以看出，槽壳侧壁的应力和应变普遍比底部应力应变大很多，这是由于侧壁主要承受阴极炭块和内衬的膨胀应力，底部槽壳主要承受电解槽的自身质量，而内部的膨胀应力要比电解槽自身质量大很多。

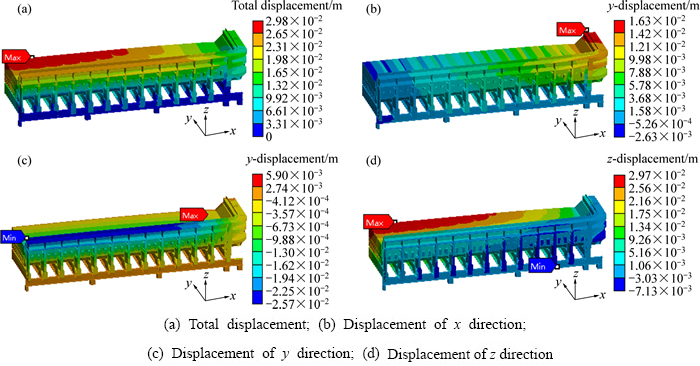
图7  位移计算结果

Fig. 7  Displacement of cell

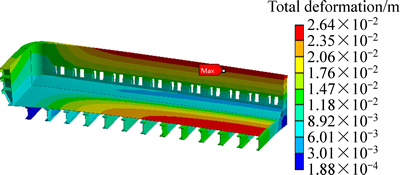
图8  槽壳摇篮架变形

Fig. 8  Deformation of pot shell

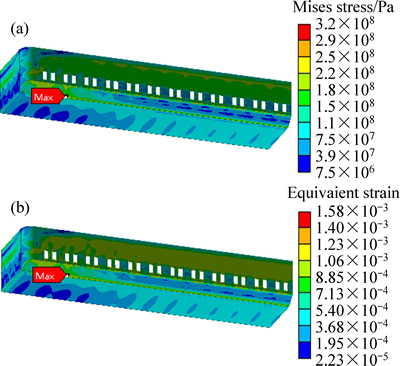
图9  槽壳Mises应力和等效应变示意图

Fig. 9  Schematic diagrams of Mises stress and equivalent strain of pot shell

图10所示为阴极炭块y方向和z方向位移分布。从y方向位移分布图中可以明显看出炭块顶部y方向位移比底部要大，这是由于炭块顶部温度和钠浓度都比底部高，于是热膨胀和钠膨胀更加剧烈，顶部向外扩张的更多。从z方向位移分布图中可以明显看出，中心部位z方向位移比边缘处要大，这是由于阴极炭块受热膨胀和钠膨胀作用向外扩张，但是边缘处被大面内衬和槽壳限制住了，于是整体向上拱，并且中心区域上拱最厉害。

图11所示为阴极炭块第一主应力。由于阴极炭块是脆性材料，所以采用第一应力强度理论进行失效判定，阴极炭块的耐压强度为34 MPa左右。从图11中可以看出，阴极炭块大部分区域第一主应力在-14~19 MPa之间，处于比较安全的范围内。在靠近槽角的阴极炭块角部存在应力集中，应力达到80 MPa左右，此处在实际生产过程中可能会产生裂纹，使应力得到释放。

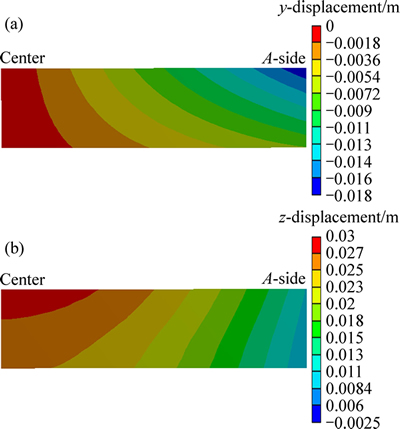
图10  阴极炭块y方向位移和z方向位移

Fig. 10  y-direction (a) and z-direction (b) displacement of cathode carbon block

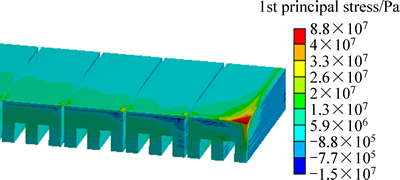
图11  阴极炭块第一主应力

Fig. 11  First principal stress of cathode carbon block

4  结论

1) 电解槽x方向和y方向最大位移分别为1.6 cm和2.6 cm，出现在小面槽壳中部和大面槽壳中部，z方向最大位移为3 cm，出现在阴极炭块上表面。这说明电解槽由于受到热膨胀和钠膨胀的作用，整体向外膨胀，并且底部向上隆起。底部摇篮架和槽壳脱开约1 cm，与实际情况吻合。

2) 槽壳最大应变为0.15%，尚未达到屈服极限0.2%，槽壳在目前的载荷条件下仍然处于弹性阶段。

3) 模型中考虑了钢的塑性变形和摩擦接触，得到了收敛的结果。计算结果和实际情况比较接近，可以为电解槽结构设计和有限元仿真提供参考。

REFERENCES

[1] 方 宁, 谢刚, 俞小花, 路 辉. 铝电解钠对阴极渗透膨胀的影响及解决方法[J]. 炭素技术, 2011, 30(1): 52-55.

FANG Ning, XIE Gang, YU Xiao-hua, LU Hui. Influence of penetration of sodium into cathode carbon blocks during aluminum electrolysis and solutions[J]. Carbon Technique, 2011, 30(1): 52-55.

[2] 李 勇. 铝电解质和金属钠对阴极炭块渗透与侵蚀的研究[J]. 四川冶金, 2011, 33(5): 66-70.

LI Yong. Research on permeation and corrosion of bath and sodium to cathode block[J]. Sichuan Metallurgy, 2011, 33(5): 66-70.

[3] 李 劼, 张红亮, 徐宇杰. 现代大型铝电解槽内复杂物理场的仿真计算与优化[J]. 中国有色金属学报, 2011, 21(10): 2594-2606.

LI Jie, ZHANG Hong-liang, XU Yu-jie. Simulated computation and optimization of comprehensive physical fields in modern large-scale aluminum reduction cells[J]. The Chinese Journal of Nonferrous Metals, 2011, 21(10): 2594-2606.

[4] 伍玉云. 300 kA 铝电解槽电热应力场及钠膨胀应力的仿真优化研究[D]. 长沙: 中南大学, 2007: 23-24.

WU Yu-yun. Study of simulation and optimization on the electro-thermo-stress field and sodium expansion stress field in 300 kA aluminum reduction cells[D]. Changsha: Central South University, 2007: 23-24.

[5] 尹诚刚, 李 劼, 徐宇杰, 杨 帅, 赖延清, 江 南, 张红亮. 新型阴极钢棒对铝电解槽电热场的影响[J]. 中国有色金属学报, 2014, 24(1): 246-253.

YIN Cheng-gang, LI Jie, XU Yu-jie, YANG Shuai, LAI Yan-qing, JIANG nan, ZHANG Hong-liang. Effects of innovative cathode collector bars on thermal-electric field of aluminum reduction cells[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(1): 246-253.

[6] 张钦菘, 杨晓东, 刘雅锋, 周东方, 刘 铭. 预焙槽的三维电热场仿真[J]. 轻金属, 2012(3): 26-29.

ZHANG Qin-song, YANG Xiao-dong, LIU Ya-feng, ZHOU Dong-fang, LIU Ming. Simulation of 3D thermoelectric field for prebaked aluminum reduction cell[J]. Light Metals, 2012(3): 26-29.

[7] 徐宇杰, 李 劼, 尹诚刚, 杨 帅, 张红亮, 吕晓军. 铝电解槽电-热场强耦合建模计算方法[J]. 中国有色金属学报, 2014, 24(1): 239-245.

XU Yu-jie, LI Jie, YIN Chen-gang, YANG Shuai, ZHANG Hong-liang, L Xiao-jun. Method of strongly coupled modeling and computing for thermal-electrical field in aluminum reduction cells[J]. The Chinese Journal of Nonferrous Metals, 2014(1): 239-245.

[8] 陶 沙. 铝电解槽三维全槽模拟研究[D]. 武汉:华中科技大学, 2005: 39-40.

TAO Sha. 3D Simulations on aluminum electrolyte cells[D]. Wuhan: Huazhong University of Science and Technology, 2005: 39-40.

[9] 邓星球. 160 kA 预焙阳极铝电解槽阴极内衬电-热-应力计算机仿真研究[D]. 长沙: 中南大学, 2004: 18-20.

DENG Xing-qiu. Structural-thermo-electric coupled simulation of the cathode lining in the 160 kA prebaked aluminum reduction cells[D]. Changsha: Central South University, 2004: 18-20.

[10] 何龙庆, 林继成, 石 冰. 菲克定律与扩散的热力学理论[J]. 安庆师范学院学报(自然科学版), 2007, 12(4): 38-39.

HE Long-qing, LIN Ji-cheng, SHI Bing. Fick Law and the diffusion’s thermodynamics theory[J]. Journal of Anqing Teachers College (Natural Science Edition), 2007, 12(4): 38-39.

[11] 刘业翔, 李 劼. 现代铝电解[M]. 北京: 冶金工业出版社, 2008: 282.

LIU Ye-xiang, LI Jie. Modern aluminum electrolysis[M]. Beijing: Metallurgical Industry Press, 2008: 282.

[12] SUN Yang, WANG Qian-pu, KETIL R, MORTEN S, HARALD A . Modelling of thermal and sodium expansion in prebaked aluminum reduction cells[C]//CREPEAU P. Light Metals. Warrendale: TMS. 2003: 603-610.

[13] 李永刚, 娄海琴, 谭丽华, 余成林, 李晓睿. 脉冲激振式耐火材料高温弹性模量测试仪及其应用[J]. 耐火材料, 2011, 45(4): 313-315.

LI Yong-gang, LOU Hai-qin, TAN Li-hua, YU Cheng-lin, LI Xiao-rui. The pulse vibration tester of elastic modulus for refractory at high temperature and its application[J]. Refractories, 2011, 45(4): 313-315.

[14] 姜志宏, 高纯生. 氧化铝熟料窑耐火砖弹性模量测定[J]. 机械设计与制造, 2011(10): 189-190.

JIANG Zhi-hong, GAO Chun-sheng. Measurement of elastic modulus of firebrick in kiln of alumina[J]. Machinery Design & Manufacture, 2011(10): 189-190.

[15] 邓星球. 160 kA预焙阳极铝电解槽阴极内衬电-热-应力计算机仿真研究[D]. 长沙: 中南大学, 2004: 40.

DENG Xing-qiu. Structural-thermo-electric coupled simulation of the cathode lining in the 160 kA prebaked aluminum reduction cells[D]. Changsha: Central South University, 2004: 40.

[16] 伍洪泽. 大型铝电解槽槽壳位移研究[J]. 中国有色金属学报, 1997, 7(2): 65-68.

WU Hong-ze. Displacement study on the shell of an aluminum electrolyzer[J]. The Chinese Journal of Nonferrous Metals, 1997, 7(2): 65-68.

Calculation of sodium diffusion in cathode blocks and coupled computing of thermal-stress in aluminum reduction cells

WANG Heng¹, ZHOU Kai-qi¹, ZHOU Zhong-qiang², HUANG Jun²

(1. Faculty of Mechanics, Huazhong University of Science and Technology, Wuhan 430074, China;

2. Guiyang Aluminum-Magnesium Design and Research Institute Co., Ltd., Guiyang 550081, China)

Abstract: The finite element model of the thermal stress and sodium expansion coupling in the aluminum reduction cell was established by using workbench ANSYS simulation platform. The sodium diffusion of the cathode carbon block was obtained by using the similarity between non steady state mass diffusion and the transient heat conduction. The sodium expansion coefficient was converted into the thermal expansion coefficient according to the distribution of sodium concentration, which can realize the indirect coupling between sodium expansion and thermal expansion. The plastic deformation and friction contact of steel were considered, the calculation results agree well with the actual situation.

Key words: aluminum reduction cell; sodium diffusion; thermal stress; sodium expansion; finite element method

Foundation item: Project(2013DFB70220) supported by International Science and Technology Cooperation Program of China

Received date: 2015-08-11; Accepted date: 2016-02-24

Corresponding author: HUANG Jun; Tel: +86-13985525605; E-mail: hjiajun@163.com

 (编辑  李艳红)

基金项目：国家国际科技合作专项项目(2013DFB70220)

收稿日期：2015-08-11；修订日期：2016-02-24

通信作者：黄  俊，高级工程师；电话：13985525605；E-mail：hjiajun@163.com