J. Cent. South Univ. (2017) 24: 374-381

DOI: 10.1007/s11171-017-3439-y

Unsteady temperature field of surrounding rock mass in high geothermal roadway during mechanical ventilation

ZHANG Yuan(张源)^{1, 2}, WAN Zhi-jun(万志军)^{1, 2, 3}, GU Bin(顾斌)¹,

ZHOU Chang-bing(周长冰)¹, CHENG Jing-yi(程敬义)³

1. School of Mines, China University of Mining and Technology, Xuzhou 221116, China;

2. Key Laboratory of Deep Coal Resource Mining of Education Ministry, China University of Mining and

Technology, Xuzhou 221116, China;

3. State Key Laboratory of Coal Resources and Safe Mining, China University of Mining and Technology,Xuzhou 221116, China

Central South University Press and Springer-Verlag Berlin Heidelberg 2017

Abstract: To explore the spatial-temporal evolution law of rock mass temperature in high geothermal roadway during mechanical ventilation, a series of experiments were conducted based on the physical simulation test system of thermal and humid environment in high geothermal roadway, which is a method independently developed by China University of Mining and Technology. The results indicate that during ventilation, the disturbed region of the temperature extends gradually from shallow area to deep area in the surrounding rock mass of the roadway. Meanwhile, the temperature increases as the exponential function from shallow area to deep, with steady decrease of the temperature gradient and heat flux. As the ventilation proceeds, the relationship between dimensionless temperature and dimensionless time approximately meets Hill function.

Key words: high geothermal mine; heat hazard; unsteady temperature field; evolution law; mechanical ventilation

1 Introduction

With the rapid economic and social development in emerging economies, the total production and consumption of solid mineral resources keep rising year by year, which has led to the exhaustion of shallow mineral resources and the increase of mining depth. At present, human beings have been able to exploit the solid mineral resources about 4 km underground [1, 2]. As the exploitation goes deeper and deeper, high geothermal hazards would become a prominent issue affecting mine production and management. Compared with shallow mining, high geothermal temperature in deep mining is a critical factor to induce geothermal hazards. For example, in China, the temperature gradient of coal stratum is 25-30 °C/km on average. In this case, it can be inferred that the rock temperature at -1000 m will reach 40-45 °C [3]. Actually, many mines with high geothermal hazards have the temperature close to the upper limit (45 °C). For instance, in Sanhejian coal mine of Xuzhou Mining Group, China, the surrounding rock temperature of -980 m mining level is up to 46.8 °C, this value reaches 45 °C at -1180 m mining level of Suncun coal mine, Xinwen Mining Group, China; similarly, in Zhaolou mine of Yanzhou Mining Group, China, the temperature at -900 m is 43 °C[4]. Under the synthetic effect of high geothermal temperature, oxidation heat of coal and rock matrix, air compression heat and heat dissipation of electromechanical equipment, it is easy to generate high temperature environment in underground mines. According to incomplete statistics, there are nearly 150 high geothermal coal mines in China and their temperature of workface is usually 30-40 °C [5, 6]. Apparently, heat hazard has become the sixth mine disaster after roof, gas, water inrush, fire and dust.

The temperature, which exists in rock stratum without the impact of any engineering, is called original rock temperature [7-9]. Once the underground roadway is excavated, the balance state of original temperature is destroyed and the heat transfers from deep surrounding rock to air flow in the roadway, resulting in dynamic changes of temperature distribution in surrounding rock. Generally, the underground mines have a complex ventilation system with long ventilation paths. Also, with a larger exposure area, the roadways in these mines are

relatively longer in service than other mines, which would easily cause heat pollution to the air flow in the roadway. Thus, researches on temperature field will be beneficial to grasp the formation mechanism of heat hazards and explore the prevention methods, and in fact, it has already received more and more attention in recent years.

Methods usually applied to study the temperature field in the roadway rock mass are site investigation and numerical calculation. Site investigations of the roadway rock mass temperature have been conducted respectively in Huaibei Mining Group and Pingdingshan Mining Group in China by using thermocouples placed in in-situ boreholes. Results show that the disturbed region of the temperature extends gradually from shallow area to deep area in the surrounding rock mass of the roadway, and the final disturbed depth is about 25-30 m. Meanwhile, the temperature changes rapidly at the beginning of the ventilation, and the temperature variation decreases gradually with the depth increases in the roadway rock mass [10, 11]. Although in-situ observation data are relatively true, only a few data have been obtained so far because of its troublesome and costly process. Compared with site investigation method, finite element method (FEM) and finite difference method (FDM) are more usually used to research the temperature field in the roadway rock mass. Besides the results from the site investigation method, more research results are found by the numerical calculation method, concerning the rock mass temperature field prediction [12, 13], influence factors of temperature distribution in the rock mass [14-17], and the disturbed region of the temperature in the surrounding rock mass [18]. In spite of many researches on the rock mass temperature distribution of the roadway, most of the results have not been validated in laboratory. From previous studies, there is only limited site observation data about the rock mass temperature of the roadway, and it is obvious that the numerical computation method is strongly dependent on the rationality of mathematical model. On the basis of analyzing heat conduction characteristics of surrounding rock, a mathematical model has established by using cylindrical coordinate system and its unsteady modularization test method, which provides possibility of carrying out modeling experiments in laboratory [18].

Based on previous researches, the authors carried out an array of modularization experiment on temperature field of surrounding rock in high geothermal roadway, using independently developed system, i.e. physical simulation test system of thermal and humid environment on high geothermal roadway. On the basis of these research works, the characteristics of temperature distribution and its evolution law are generally obtained.

2 Experimental methods

2.1 Fundamental assumption

The shape and size of roadways are different, so are the lithology and geological conditions. Because air flow conditions keep changing, thermal conductivity of surrounding rock as well as the heat transfer between surrounding rock and flow is rather complex. To figure out the inner relationships of roadway temperature distribution and its evolution law, the following characteristics of roadway and its surrounding rock are assumed [19]:

1) The cross-section of roadway is circular and the surrounding rock has the property of continuity, homogeneity and isotropy. Also, the thermophysical parameters of surrounding rock are constant;

2) Initially, the temperature of surrounding rock is identical, which is equal to the original rock temperature;

3) The air flow temperature of roadway only changes along its axial direction and the heat transfer conditions are the same at circumference direction. Besides, air flow temperature is well-distributed in the same radial cross-section;

4) In the scope of research works, there is no temperature gradient in vertical direction of the roadway.

2.2 Experimental equipment

A series of tests have been conducted by using physical simulation test system of thermal and humid environment in high geothermal roadway, which is made up of physical simulation roadway, heating electric power, constant temperature and humidity machine, and data collection apparatus, as shown in Fig. 1. The major technical parameters are as follows:

1) Physical simulation roadway is consisted of six barrels. Each barrel is 1.0 m long with inner diameter of 0.8 m and external diameter of 1.0 m.

2) The heating mode has constant current, voltage and power, with iron chromium aluminum alloy mesh as heating element, low voltage and high current as heating method. The highest heating current is 1000 A, and the highest voltage is 30 V. An environment of steady original temperature field can be set up with temperature ranging from indoor temperature to 60 °C. The heating precision is ±0.1 °C.

3) Ventilation is carried out by constant temperature and humidity machine, with the assistance of an axial flow fan and a small air blower. The maximum quantity of air flow is 5000 m³/h and this can be continuously adjusted. The range of temperature is from 5 to 45 °C and the range of humidity is from 20% to 90% relative humidity (RH).

4) The pedestal of physical simulation roadway is tower structure with hydraulic regulating pump station and oil cylinder, which enables the inclination angle of simulation roadway to be adjusted from 0 to 45 °C.

5) The experimental system is controlled automatically by microcomputer. The data of air flow temperature, humidity, velocity, and gas pressure are also collected automatically.

Data collecting sensors including temperature sensors, air velocity sensors, humidity sensors and air pressure sensors are placed in simulated roadway, as shown in Fig. 2. Sensors monitoring air velocity and pressure are placed in air inlet and outlet of the simulated roadway instead of inside it. To promote the precision of air quantity control, an extra air velocity sensor is placed on the pipeline of constant temperature and humidity machine outlet. Six humidity sensors are fixed in each cylinder connection and they are all located in the center of simulated cylinder. In the axial center of 6 cylinders, five thermocouples are placed in equal distance to monitor temperature data on radial direction.

According to the requirements of simulated surrounding rock, and considering the impossibility of adopting original structure material in such large-size and large-scale modeling experiment, Portland cement-based material is chosen as the desired material. The thermal conductivity of cement mortar is basically under 1.0 W/(m·K), thus a certain proportion of heat-conducting powder is necessarily added to promote the heat-conducting property. High-purity quartz sand has favorable heat-conducting performance, and its thermal conductivity is several or tens of times of that of river sand. Contrasted with coarse aggregates such as marble and granite, the heat conducting capacity of iron powder or Fe₂O₃ is beyond comparison and their particle sizes are small and easy to dissolve into grout, thus a small amount is sufficient. Based on the above analysis, small proportion of high purity quartz sand and river sand are included as fine aggregates, and Fe₂O₃ powder is involved to increase its heat-conducting property. Simulated surrounding rock of roadway is shown in Fig. 3.

2.3 Experimental program and procedure

According to upper limit of first class heat hazard and lower limit of second class heat hazard of China mine engineering standards, the experimental original rock temperature is set as 37 °C [20]. To simplify the tests, the mass transfer process between air flow and surrounding rock mass is neglected. The humidity of air flow is 20% RH invariably. The air flow temperature is divided into two groups, i.e. 10 °C and 20 °C, while the air flow velocities are also in two sets as 5 m/s and 8 m/s, respectively. The test procedures are as follows:

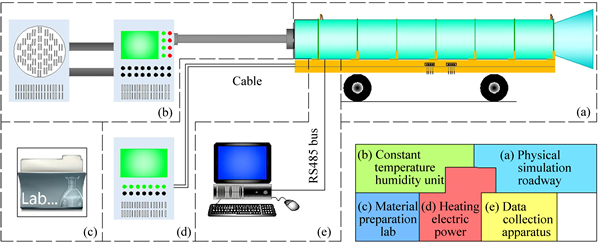
Fig. 1 Component of physical simulation test system of thermal and humid environment in high geothermal roadway

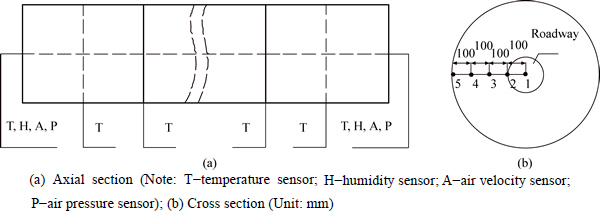
Fig. 2 Arrangement of temperature observation points in simulated roadway:

Fig. 3 Simulated surrounding rock of roadway (Unit: mm)

1) Install the simulation surrounding rock mass into the physical simulation roadway. Turn on the rectifier power after the heating alloy mesh and sensor are correctly connected, then test the working conditions of heating element to ensure that the total resistance of heating alloy mesh is no more than 0.03 Ω.

2) Take the outer boundary of simulation roadway as the temperature control point and set the upper limit of temperature control point as original rock temperature (37 °C). The lower limit value is about 0.2 °C less than that of upper limit. If the temperature exceeds the upper limit, the heating will be suspended automatically; while if the temperature is under the lower limit, the heating procedure will restart automatically.

3) Set the heating mode into automatic steady flow heating and adjust the output current into ladder decreasing from 300 to 100 A, with a declining rate of 50 A/h. Each heating period will last for about 2 h.

4) Start the heating procedure and then change the heating mode from automatic control into manual control until the temperature of simulation surrounding rock mass is close to the original rock temperature. To make the temperature of all measure points steady, approximation method is applied to repeatedly regulate the current within 20-100 A;

5) When the temperature of all test points is steady and constant, keep warm for 6 to 8 h;

6) Open the constant temperature and humidity machine and the assistant air blower, adjust the air flow temperature to 10 °C, humidity to 20% RH, air flow velocity to 5 m/s (Scheme 1), then blow the air into the simulation roadway;

7) When the temperature of control points drops to 36.6 °C, which is about 1% lower than original rock temperature, stop the constant temperature and humidity machine, as well as the auxiliary fan. Save data and move on to the heating procedure of next experiment;

8) Repeat steps 4)-7), conduct the experiment with the air flow temperature of 20 °C, velocity of 5 m/s (Scheme 2);

9) Repeat steps 4)-7), finish the test with the air flow temperature of 20 °C, velocity of 8 m/s (Scheme 3);

10) Turn off the heating power, collate data and close the experiment.

3 Experimental results and analysis

3.1 Method for data analysis

To acquire the fundamental laws among surrounding rock mass temperature, space and time, dimensionless method is used to process the three parameters.

                          (1)

where Θ is the dimensionless temperature, t is the temperature of surrounding rock mass in the roadway, t_f is the air flow temperature, t₀ is the original rock temperature, R is the dimensionless radius, r is the distance between the measure points to the central point of roadway, F_o is the dimensionless time, a is the thermal diffusivity of the roadway, τ is the ventilation time, r₀ is the radius of the roadway.

3.2 Temperature distribution characteristics of surrounding rock mass under ventilation

As we can see in Fig. 4, the experimental data of Scheme 1(10 °C, 20% RH, 5 m/s), Scheme 2(20 °C, 20% RH, 5 m/s) and Scheme 3(20 °C, 20% RH, 8 m/s) indicate similar tendency on their relation curves between dimensionless temperature and dimensionless radius.

Figure 4 suggests that from roadway wall (R=1) to deep area, the temperature gradually rises to the original rock temperature (the experimental temperature is set as 37 °C, and the dimensionless temperature is 1). When the value of F_o is 0.1, the excess temperature (t-t_f) of roadway wall immediately falls within 0.8 time of the initial excess temperature (t₀-t_f), then the amplitude of decline becomes smaller and smaller. Meanwhile, as the ventilation moves on, the range of temperature disturbance expands slowly. When the value of F_o is 0.1, the range of temperature disturbance is controlled within 2R (twice of the radius); when the value of F_o is 0.3, this figure is around 3R; when the value of F_o is 0.8, the range is about 4R.

The slope of the temperature-radius curve is equal to temperature gradient of surrounding rock mass 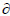t/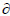r (which has a linear conversion relation with 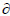Θ/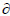R). Therefore, the temperature gradient at the roadway wall is maximal and this parameter decreases gradually with the increase of surrounding rock mass depth. Because ofthe constant thermophysical property of surrounding rock mass, to some degree, the tendency of temperature gradient changes can represent the variation trend of heat flux. A conclusion thus can be made that the heat flux also decreases gradually.

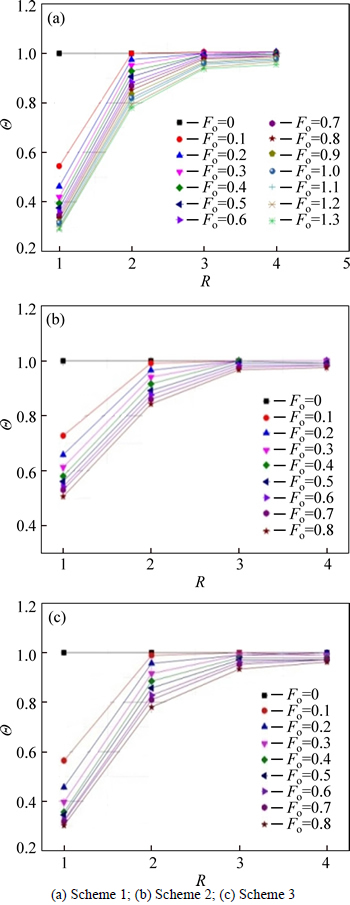
Fig. 4 Relation curves between dimensionless temperature and radius:

3.3 Temperature evolution law of surrounding rock mass under ventilation

As illustrated in Fig. 5, the temperature distribution patterns of roadway surrounding rock mass in the three experiments are consistent with each other.

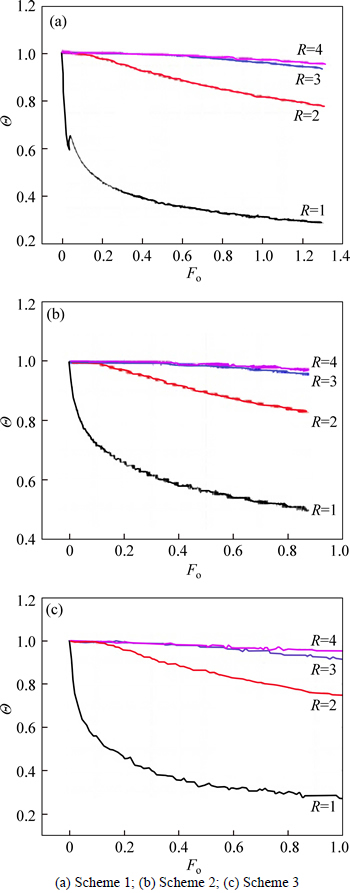
Fig. 5 Dynamic variation laws of dimensionless temperature:

In Fig. 5, after ventilation, temperature at roadway wall (R=1) first decreases dramatically. A moment later, when the value of F_o exceeds 0.1, the temperature of surrounding rock mass experiences a clear reduction where R is equal to 2, followed by the temperature decline where the values of R are 3 and 4, respectively. This shows that the range of temperature disturbance expands slowly from roadway wall to deep area, and with the progress of ventilation time, the surrounding rock temperature decreases continuously with smaller and smaller amplitude. In this circumstance, when the value of F_o approaches 0.8, the curve of dimensionless temperature and dimensionless time becomes flat.

As the simulated surrounding rock mass of 6 m is not thick enough, and the duration of experiment is limited, the authors do not record the stage when the temperature distribution is steady in general.

4 Discussion

Take Scheme 2 as an example. The fitting formula of dimensionless temperature and dimensionless radius curve indicates that the experimental results have a significant correlation with exponential function, and the goodness-of-fit index can all reach 0.99, as shown in Table 1. The expression can be described as follows:

Θ=a×exp(b×R)+c                             (2)

Table 1 Relation formula between dimensionless temperature and dimensionless radius

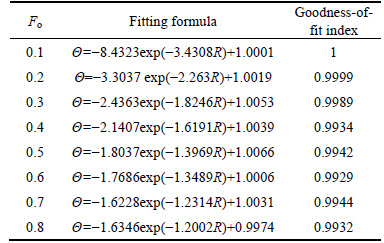
In the preliminary stage of ventilation, temperature changes dramatically in the surrounding rock mass, which is reflected in the great variation of parameter a and b in the fitting formula. With the increase of ventilation time, the absolute values of a and b both present a decreasing trend, so does the changing amplitude. Thus, parameters a and b may have a correlation with dimensionless time.

When the scope of F_o falls into 0.8-1, the value of c has stayed around 1. Θ=1 represents that the surrounding rock mass has initial temperature. When R is infinite, the value of a×exp(b×R) is close to 0 while Θ approaches 1. Actually, the temperature at positions of infinite distance is relatively steady, and is equal to original rock temperature, i.e. the value of Θ is also close to 1. Therefore, it is reasonable that formula (2) can be written as the following equation:

Θ= 1-f₁(F_o, O)×exp[f₂(F_o, O)×R]                 (3)

where O is the other influence factors apart from F_o. f₁(F_o, O) is equal to -a, while f₂(F_o, O) equals b, both f₁ and f₂ are the functions of dimensionless time F_o and Biot [20].

Similarly, as shown in Table 2, the fitting formula of dimensionless temperature and dimensionless time shows that the correlation between dimensionless temperature and heat conduction dimensionless time is approximately HILL function, i.e.

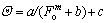                           (4)

where the values of parameter c are all close to 1; in addition, the values of m, a and b are closely connected to dimensionless radius R. For the roadway wall where R is 1, when F_o approaches infinite, Θ is close to zero, suggesting that with the progress of ventilation time, the temperature of roadway wall approaches air flow temperature. So, after infinite ventilation, the temperature of roadway wall is almost equal to air flow temperature. This is also the theoretical background of taking roadway wall temperature as air flow temperature when establishing the steady heat conduction model of surrounding rock mass.

Table 2 Relation formula between dimensionless temperature and dimensionless time

However, in the deep area of the roadway, when F_o approaches infinite, Θ is not equal to 0 and Θ/_R=1(approximately 0)<Θ/_R=2(0.6909)<Θ/_R=3(0.7896)< Θ/_R=4(0.8922). Therefore, even if the ventilation time is infinite, temperature of deep surrounding rock mass would stop as a relatively stable value rather than decreasing without limitation. Besides, it is testified that the deeper the roadway, the higher the temperature. According to the above analysis, formula (4) can be modified into the following formula:

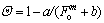                           (5)

The previous study [13] has built a mathematical heat conduction model and adopted finite difference method to study the temperature field of roadway surrounding rock mass. The research results are displayed in Fig. 6. Figure 6(a) is the relation curve of dimensionless radius and dimensionless temperature with three time scales of day, month and year. Figure 6(b) is the variation curve of dimensionless temperature within 5 times of roadway radius.

Comparing Figs. 4-6, it can be summarized that acquired from physical similarity and numerical simulation experiments, the Θ-R and Θ-F_o relation curves are basically consistent. This reveals that thetemperature distribution of surrounding rock mass meets the exponential function and the dimensionless temperature matches HILL function with dimensionless time, as shown in Fig. 7.

Fig. 6 Numerical computation results of temperature field [13]:

The above analysis suggests that at any position of the surrounding rock, the temperature can only infinitely close to but no less than the air flow temperature. The conclusion is easy to be testified. If there is such a position existing in the roadway, whose temperature is lower than air flow temperature after cooling, then the roadway is supposed to absorb the heat from the air flow, which is obviously impossible. Similarly, when the initial temperature is lower than the air temperature, the surrounding rock would absorb heat, no position may have higher temperature than that of the air flow. Thus when the initial rock temperature of roadway is higher(lower) than the air flow temperature, in the process of unsteady heat conduction, there is no position with temperature lower(higher) than the airflow temperature.

Fig. 7 Temperature field evolution of surrounding rock mass of roadways

Any position in the surrounding rock should have to absorb heat transmitted from its adjacent deep surrounding rock, but also transmit its heat to adjacent shallow surrounding rock. With the advancing of unsteady heat conduction, temperature at any position of the surrounding rock begins to decline. The heat released is definitely larger than absorbed, so that its internal energy can be lowered. Therefore, when ventilation cooling is adopted in high geothermal roadway, the heat dissipated of any position must be larger than its heat absorbed.

5 Conclusions

1) Immediately after ventilation, roadway wall temperature decreases dramatically and then approaches air flow temperature; with the progression of ventilation time, the range of temperature disturbance expands from roadway wall to deep area of the roadway.

2) After ventilation for a while, with the rising of distance between measure point and roadway wall, temperature of surrounding rock mass increases gradually, whereas, the temperature gradient, heat flux and heat flow rate decrease synchronously. The correlation between dimensionless temperature and dimensionless radius matches the exponential function.

3) As the ventilation time gets longer and longer, the surrounding rock mass temperature decreases slowly, the amplitude of this change gradually falls with the proceeding of ventilation time. The correlation between dimensionless temperature and dimensionless time matches HILL function.

References

[1] SURHONE L M, TENNOE M T, HENSSONOW S F. Tautona Mine [M]. Beau Bassin: Betascript Publishing, 2011.

[2] RANKIN W J. Minerals, metals and sustainability: Meeting future material needs [M]. Collingwood, Victoria: Csiro Publishing, 2011.

[3] XIE He-ping, ZHOU Hong-wei, XUE Dong-jie, WANG Hong-wei, ZHANG Ru, GAO Feng. Research and consideration on deep coal mining and critical mining depth [J]. China Coal Society, 2012, 37(4): 535-542. (in Chinese)

[4] WAN Zhi-jun, ZHANG Yuan, CHENG Jing-yi, ZHOU Chang-bing, GU Bin, ZHOU Peng. Mine geothermal and heat hazard prevention and control in China [J]. Disaster Advances, 2013, 6(S5): 85-93.

[5] ZHANG Yuan. Transient temperature field of surrounding rock of the high geothermal roadway and its heat control mechanism by heat insulation [D]. Xuzhou, China: China University of Mining and Technology, 2013. (in Chinese)

[6] XIE Ben-xian, CHEN Yuan-jiang, SHI Xiu-zhi. IRMR method for evaluation of surrounding rock quality in deep rock mass engineering [J]. Journal of Central South University (Science and Technology), 2007, 38(5): 987-992. (in Chinese)

[7] WASILEWSKI S, BRANNY M. A preliminary study of the unsteady states of the ventilation parameters at the longwall face during the shearer operation [C]// 12th U.S. North American Mine Ventilation Symposium. Reno, NV (USA), 2008: 107-114.

[8] KNECHTEL J. Thermal hazard prevention in longwalls run under extreme geothermal conditions [J]. Archives Min. Sci., 2011, 56(2): 265-280.

[9] YAN Hong, ZHANG Ji-xiong, LI Lin-yue, FENG Rui-min. Stability assessment of rock surrounding an I-beam supported retreating roadway [J]. Journal of Central South University, 2015, 22(9): 3598-3607.

[10] ZHU Ting-hao. Study on influence law of ventilation time to temperature of surrounding rock [J]. Safety in Coal Mines, 2010, 424(2): 10-13. (in Chinese)

[11] WU Qiang, QIN Yue-ping, GUO Liang, TAN Kun. Analysis of unsteady temperature field in wall rock by finite element method [J]. J Liaoning Technol Univ, 2002, 21(5): 604-607. (in Chinese)

[12] MA L N, YAN S H, ZHANG R L. Heat damage of high-temperature rock tunnel by weighted residual method in tibet plateau [J]. Advanced Materials Research, 2013, 790: 259-263.

[13] ZHANG Yuan, WAN Zhi-jun, ZHOU Chang-bing, PEI Song. Spatial-temporal distribution characteristics of surrounding rock temperature in high geothermal roadway [J]. Disaster Advances, 2013, 6(S5): 102-108.

[14] ZHANG Shu-guang. Numerical simulation analysis of temperature field in surrounding rock of deeply buried roadways [J]. Sci Technol and Eng, 2006, 6(14): 2194-2196. (in Chinese)

[15] GAO Jian-liang, YANG Ming. Analysis of the factors influencing temperature distribution of surrounding rock and cooled zone radius [J]. J China Safety Sci, 2005, 15(2): 73-76. (in Chinese)

[16] ABDOUS M A, AVVAL H B, AHMADI P. Analysis of transient heat conduction in a hollow sphere using duhamel theorem [J]. International Journal of Thermophysics, 2012, 33(1): 143-159.

[17] TAN Xian-jun, CHEN Wei-zhong, YANG Dian-sen. Study on the influence of airflow on the temperature of the surrounding rock in a cold region tunnel and its application to insulation layer design [J]. Applied Thermal Engineering, 2014, 67(1): 320-334.

[18] PAN Xiao-li, ZHANG Xue-bo. Analysis on influence of temperature distribution in strata rock and difference method [J]. Coal Eng, 2011, (11): 82-84. (in Chinese)

[19] ZHANG Yuan, WAN Zhi-jun, GU Bin, ZHOU Chang-bing, CHENG Jing-yi. Modeling experimental method of unsteady heat conduction in surrounding rock of roadways or tunnels [J]. Journal of Mining & Safety Engineering, 2014, 31(3): 441-446. (in Chinese)

[20] YANG De-yuan, YANG Tian-hong. Thermal environment in mine and its control [M]. Beijing, China: Metallurgical Industry Press, 2009. (in Chinese)

(Edited by FANG Jing-hua)

Cite this article as: ZHANG Yuan, WAN Zhi-jun, GU Bin, ZHOU Chang-bing, CHENG Jing-yi. Unsteady temperature field of surrounding rock mass in high geothermal roadway during mechanical ventilation [J]. Journal of Central South University, 2017, 24(2): 374-381. DOI: 10.1007/s11171-017-3439-y.

Foundation item: Project(2014-6121) supported by Fundamental Research Funds for the Central Universities, China; Project(51504236) supported by the National Natural Science Foundation of China; Project supported by the Priority Academic Program Development of Jiangsu Higher Education Institutions, China

Received date: 2015-08-17; Accepted date: 2015-12-15

Corresponding author: ZHANG Yuan, Lecturer, PhD; Tel: +86-516-83995673; E-mail: zhangyuan@cumt.edu.cn