DOI: 10.11817/j.issn.1672-7207.2016.02.036

基于动态强度折减法矿柱渐进失稳演变规律

姜立春¹，魏叙深¹，吴爱祥²

(1. 华南理工大学 土木与交通学院，广东 广州，510640；

2. 北京科技大学 土木与环境学院，北京，100083)

摘要：提出基于动态强度折减法分析矿柱渐进失稳演变的方法，揭示矿柱渐进失稳演变规律。通过理论分析，给出平面应变模型的屈服接近度指标Y，确定矿柱破损区域。利用某大型金矿工程实例，构建FLAC矿柱失稳数值模型。随着循环动态折减计算，破损区首先出现在矿柱4个边角部位，逐渐向底部中心区域扩展，直至贯通整个矿柱。破损区演变可分为稳定、扩展、突变等3个过程；随着迭代计算步长增加，破损单元数量由缓慢增加、稳定增加到急剧扩展。与整体强度折减法相比，该方法准确揭示矿柱渐进破坏机理，客观描述矿柱渐进失稳演变趋势和变形破坏程度，克服容易人为夸大破损区、产生不正常破损区的缺憾。现场位移监测结果验证了该方法分析结果的正确性。动态强度折减法为研究矿柱失稳机理和安全评价提供了一种新的有效方法。

关键词：矿柱；动态强度折减法；屈服接近度；临界失稳；模型

中图分类号：TD315             文献标志码：A         文章编号：1672-7207(2016)02-0621-07

Gradual evolution law of pillar based on dynamic strength reduction method

JIANG Lichun¹, WEI Xushen¹, WU Aixiang²

(1. School of Civil Engineering and Transportation, South China University of Technology, Guangzhou 510640, China;

2. School of Civil and Environmental Engineering,

University of Science and Technology Beijing, Beijing 100083, China)

Abstract: In order to reveal gradual evolution law of pillar, dynamic strength reduction calculation methods was proposed for analyzing pillar progressive failure process. Through theoretical analysis, yield proximity indicators Y in plane strain model was used to determine the damaged region of pillar. The pillar instability numerical model was constructed with FLAC based on a large-scale mining. With the dynamic cycle reduction calculation, pillar damage appeared from the corners firstly, and then gradually to the bottom center and evolved to breakthrough. The evolution of damaged area can be divided into three processes including stabling, expanding and mutating. As the iterative step length increases, the number of damaged cells increases from slowly to stably and then expands rapidly. Compared with the overall strength reduction, the method accurately reveals the pillar progressive failure mechanism and objectively describes the evolution trend of gradual evolution and pillar deformation, which overcomes the shortcomings of artificially inflating damaged area and producing abnormal damaged area. The correctness of the analytical result is verified by in-site displacement monitoring result. Dynamic strength reduction method provides effective way for research on pillar failure mechanism and safety evaluation.

Key words: pillar; dynamic strength reduction; yield proximity indicators; critical instability; model

矿柱失稳破坏是一个复杂非线性变化过程，探寻其失稳模式及破坏演变机理，可以有效预防由此诱发的工程地质灾害。近年来，国内外学者对矿柱渐进性破坏过程开展了研究^[1-6]。WALLACE等^[1]采用室内实验方法，分析和预测矿柱结构渐进式坍塌过程；宋义敏等^[2]利用煤试件单轴压缩加载试验，分析了煤柱变形产生、演变以及失稳过程的能量演变；王学滨^[3]采用拉格朗日元法，模拟了屈服矿柱的剪切带图案、渐进破坏特征、水平应力及垂直应力分布及演变规律；刘增辉等^[4]采用数值正交实验方案评价金川二矿区水平矿柱的稳定性；马海涛等^[5]针对不规则点柱支撑顶板的复杂采空区结构，采用Voronoi图形划分法，提出了模拟矿柱破坏荷载转移过程的计算方法。目前，国内外学者主要通过加载试验、数值模拟等方法开展相关研究，很少从岩体自身局部强度弱化的角度进行分析。事实上，矿柱的破坏主要是由岩体局部渐进性破坏引起的，因此，从岩体局部强度弱化的角度开展失稳机理研究，具有十分重要的意义。强度折减法能够反映岩体的非线性关系，通过降低岩体物理力学参数性征，建立岩体失稳的定量关系^[6]。强度折减法可分为整体强度折减法和动态强度折减法2种方法。整体强度折减法进行数值计算，容易出现大面积屈服单元，不能客观反映矿柱渐进破坏过程。动态强度折减法通过量化单元屈服接近程度，对岩体破损单元的力学参数进行动态折减，研究工程体渐进失稳演变过程。目前，该方法开始应用于边坡失稳分析，但少有应用于矿柱失稳分析的报道^[7-8]。本文作者将动态强度折减法引入矿柱失稳研究中，探寻矿柱渐进破坏的机理，揭示矿柱的破损区演变过程和变形破坏程度，利用某大型地下金矿现场位移监测数据，验证该方法分析结果的可靠性，为矿柱失稳机理研究和安全评价提供一条新途径。

1  矿柱渐进失稳分析

1.1  破损单元力学参数折减计算

动态强度折减法通过折减破损区域的岩体物理力学参数，即将变量(c和tan φ)同时除以折减系数K，获得一组新的强度参数，作为下一轮计算的参数，如下式所示。

           (1)

式中：c为岩体初始黏聚力；φ为岩体初始内摩擦角；c_loc为岩体破损单元的黏聚力；φ_loc为岩体破损单元的内摩擦角。

1.2  平面模型单元屈服接近度指标Y计算

文献[6]在反映单元材料的非线性特征时引入了屈服接近度的概念，基于Mohr-Coulomb破坏准则(图1)，通过应力圆与破坏包络线的关系定义屈服接近度指标Y₀。

         (2)

式中：D₁为应力圆心到直线强度包络线的距离；D₂为应力圆心与单轴抗拉强度对应点在主应力轴上的距离；d₁为应力圆与直线强度包络线的最短距离；d₂为最小主应力点与单轴抗拉强度值对应点在主应力轴上的距离。

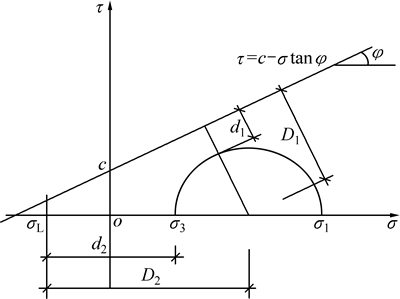
图1  屈服接近度的Mohr圆示意图

Fig. 1  Sketch map of failure approach degree by method of Mohr circle

三维模型中，单元屈服接近度指标的计算公式^[10]为：

  (3)

              (4)

  (5)

        (6)

式中：I₁为应力张量第一不变量；J₂为应力偏量第二不变量；θ_σ为应力罗德角；σ₁，σ₂和σ₃分别为最大主应力、中间主应力和最小主应力。

矿柱破损失稳是三维空间轴向形变的过程，通常是由于某个轴向出现大的位移变形引发的。现有位移监测也是针对某个变形大的轴向进行监测，为了简便计算分析，这里采用平面模型进行计算分析。

结合广义胡克定律，求取平面模型的单元屈服接近度指标Y。

          (7)

令ε₂=0，可得

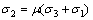              (8)

联立式(3)~(6)和式(8)，可求解Y。

经计算，屈服接近度Y值域为[0，1]。当Y=0时，岩体单元应力点发生屈服破坏；当Y=1时，岩体单元处于最安全状态。当屈服接近度位于0~0.2的范围时，岩体单元临近屈服状态，外部扰动极易造成屈服，可将其视为损伤区。

因此，矿柱的破损区为塑性区(Y=0)和损伤区(0＜Y＜0.2)之和。

1.3  计算步骤

动态折减矿柱破损区单元的物理力学参数，循环计算，致使矿柱破损区逐渐扩展，直至处于突变失稳状态。计算步骤如图2所示。

1) 矿柱建模。

2) 初始应力加载。

图2  动态强度折减法的矿柱渐进破坏分析步骤

Fig. 2  Analysis of progressive failure process for pillar based on dynamic strength reduction method

3) 数值模型初始计算。确定岩体的黏聚力c和内摩擦角φ初始值，进行数值模型计算，直至系统收敛。

4) 破损区的确定。当岩体单元Y小于0.2时为破损区；若无单元发生破损，则增加折减系数K，重新进行数值模型计算，直至矿柱单元发生破损为止。

5) 折减破损单元力学参数，模型重新进行数值 计算。

6) 重复第4)和5)步骤。折减新的破损区岩体力学参数，进行数值模型计算，进一步延伸破损区范围。

7) 结束。当矿柱出现突变失稳现象时，停止进行参数折减计算，分析过程结束。

1.4  失稳判定

目前，数值分析计算时，工程岩体失稳的判据方法主要归纳为以下3种：1) 塑性区贯通；2) 计算不收敛；3) 关键点的位移发生突变或者无限发展。由于塑性区贯通是破坏的必要但非充分条件，不能单独作为失稳的判据^[14]。因此，这里选用系统不收敛和关键点位移突变，判定矿柱失稳。

2  实例分析

2.1  工程概况

某大型金矿位于秦岭褶皱系南秦岭印支褶皱带凤县—镇安褶皱束的北缘，含金角砾岩带(A_nK_sb)主要分布于泥盆系中统古道岭组地层中，矿床赋存于该含金角砾岩带。地层主要由泥盆系中统的王家楞组(D_2W)、古道岭组(D_2g)的碎屑岩和碳酸岩组成。矿山由KT8，KT5，KT9，KT7，KT2和KT6这6个矿体组成，主要采用阶段崩落法辅助浅孔留矿法进行回采。

经过多年的回采，矿山遗留大量的采空区，多次发生地压灾害，地压问题严重。其中，最大一次地压灾害发生在2010-12，KT5矿体1 670 m中段71线附近，采空区突然坍塌，激发高速冲击波，导致相邻采场及周边开拓工程体严重破损。

KT5矿体主要采用浅孔留矿法开采，盘区工作面位于1 420 m中段，距离地表垂直高度为240.5 m。盘区开采顺序为先回采矿房I，再回采矿房II，最后形成矿柱支撑采空区(图3)。矿房I和矿房II的跨度为45.3 m，矿柱高为30.2 m，宽为10.5 m。

2.2  模型构建

利用FLAC软件，构建矿柱失稳计算数值模型(图3)。模型宽为400 m，高为410 m，由34 180个单元组成。岩体破坏服从Mohr-Coulomb屈服准则。模型采用底边界、侧边界位移约束，初始应力为岩体的自重应力。为了提高计算精度，对矿柱区域进行加密细分处理。

依据矿山岩体实测数据，模型的物理力学参数选取如表1所示。

图3  数值模型示意图

Fig. 3  Diagram of numerical model

表1  岩体物理力学参数

Table 1  Physical and mechanical parameters of rock

2.3  计算分析

分别采用动态强度折减法和整体强度折减法分析矿柱渐进失稳过程。设定折减系数增量ΔK=0.1，由式(1)计算，可得每个计算循环的物理力学参数(表2)，计算流程如图2所示。

2.3.1  基于动态强度折减法矿柱失稳演变规律

1) 矿柱破损区演变。矿柱的破损区演变如图4所示。经过计算，破损区首先发生在应力相对集中的4个边角部位，逐渐向矿柱底部中心区扩展，直至两翼破损区相互贯通。

经1~13次循环折减计算，折减系数K在1.1~2.3之间，矿柱破损区发展相对缓慢，见图4(a)~(d)。经14~16次循环折减计算，折减系数K从2.4增加至2.6，矿柱破损区域迅速扩展；至第16次折减时，矿柱底部破损区左右贯通，见图4(e)~(f)。随着迭代步数的增加，破损区域进一步扩大。

由矿柱破损单元数量随时间增加趋势图可以发现(图5)：破损区的扩展可以分为3个阶段：1) 稳定期。随着时间增加，破损单元数量增长缓慢；2) 扩展期。随着时间增加，破损单元数量稳定增长；3) 突变期。破损单元数量急剧增长，矿柱底部两翼破损区域相互贯通。

矿柱变形演变过程与矿柱周边围压、应力传递密切相关。由于矿柱根部边缘的围压较低，岩体单元处于近似平面应变单轴压缩状态，极限抗压强度较低。因此，破损区首先出现矿柱边角部位。

矿柱中部岩体单元围压较高，单元体处于应变双轴压缩状态，极限抗压强度较高。当边角部位单元破损后，矿柱体应力分布重新调整，形成新的应力集中区域，逐渐向矿柱中心区域转移。矿柱应变较高时，该区域才可能发生破损破坏。

同时，随着破损单元数量的增加，矿柱有效承载单元体数量减少，岩体单元承载应力增加，应变逐渐增大，最终导致矿柱中心部位出现破损单元，从而诱发矿柱整体失稳。

2) 系统不平衡力。  矿柱失稳破坏折减过程中，系统不平衡力变化趋势图如图6所示。由图6可见：随着折减次数的增加，不平衡力的波动幅值增大，系统自稳调整时间延长。

折减计算初期(1~13次)，随着迭代步长增加，不平衡力逐渐收敛。表明矿柱经历了局部变形破损后，系统最终趋于亚稳定状态。

表2  力学参数折减表

Table 2  Reduction of physical and mechanical parameters

图4  动态强度折减计算矿柱破损区演变过程

Fig. 4  Evolution of damage zone of pillar under dynamic strength reduction

图5  破损单元数量变化趋势图

Fig. 5  Trend of number of damaged cells growing

图6  系统不平衡力变化曲线

Fig. 6  Unbalanced force changes in trace chart

当经过16次循环折减后，系统不平衡力开始出现大幅波动。随着迭代步长的增加，系统也无法收敛。

系统不平衡力变化曲线表明(图6)，在破损区的稳定期和扩展期，矿柱处于稳定状态；当进入突变期后，局部出现严重塑性变形，矿柱处于不稳定状态。

2.3.2  整体强度折减法

为了对比分析，采用传统整体强度折减法对相同的矿柱进行了失稳分析。将矿柱整体单元的黏聚力c和内摩擦角φ进行依次折减，计算结果如图7所示。

从图7可以发现：破损区同时出现在矿柱边角和中心区域(图7(a))，破损区域迅速连通(图7(b))。第8次折减计算后，矿柱整体为破损区，基本处于失稳状态(图7(c))。

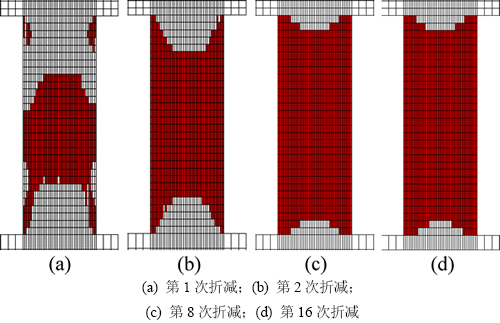
图7  整体强度折减法计算矿柱破损区演变过程

Fig. 7  Evolution of damage zone of pillar under whole strength reduction

图8所示为整体强度折减法中岩体单元应力状态图。图8中虚线应力圆代表中部单元的应力状态，实线应力圆代表边缘单元的应力状态。

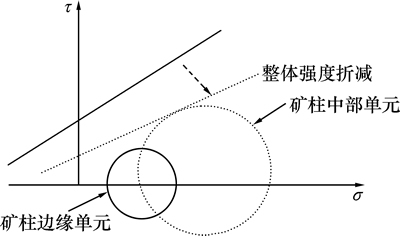
图8  整体强度折减法中岩体单元应力状态

Fig. 8  Stress state of rock element by strength reduction method

在整体折计算过程中，由于单元体受到双轴方向挤压，导致中心单元的应力高于边缘单元的应力。循环折减物理力学参数后，剪切强度包络线重心下移，中心部位单元将首先进入屈服状态，出现塑性破损区。

与动态折减法分析结果(图7和图8)相比，整体强度折减法计算的矿柱破损区，前期演变迅速而中后期演变缓慢。主要原因是：1) 后者采用位移型协调元本身的插值模式，导致了获得的矿柱破损区被人为夸大^[15]；2) 整体强度折减法人为地改变了正常应力传递过程，中部单元围压提前降低，导致出现不正常的破损区。

而动态强度折减法只对破损区域的参数进行折减，在计算过程中，动态搜索矿柱潜在的破损区，更符合矿柱的真实失稳特征。

2.4  现场分析验证

现场观察表明：当矿柱两翼的矿房I、矿房II回采结束后，在1 450 m中段上部岩体荷载的作用下，矿柱底部出现破损区。底部初期出现微裂纹，肉眼不易察觉；25 d后，底部出现明显的裂缝；随着时间的增加，裂缝不断扩展，最终形成长度约为8 m的剪切裂面，几乎贯穿矿柱整个截面(图9)。

位移监测结果表明(图10)：矿柱破损区演变过程分为稳定期、扩展期和突变期3个阶段。在稳定期和扩展期，监测点水平位移幅值较小；随着时间的推移，破损区裂纹逐渐扩展成裂缝，裂缝扩展成破裂面，位移变形出现大的跃升，进入变形突变期。

动态强度折减法、整体强度折减法计算结果与现场位移监测结果对比表明(图10)：动态强度折减法计算结果与现场监测点的变化趋势基本一致，位移变化幅值相当；整体强度折减法计算结果与监测结果差异较大，在相同的时间步长内，位移变化幅值相差1.5~3.0倍，位移变化趋势也不尽相同。

由于动态强度折减法通过合理量化矿柱单元的屈服接近度，适用于含弱面等非均质矿柱的失稳分析。综上对比分析可知：动态强度折减法分析结果能够准确揭示矿柱破损区变化、演变规律，客观反映了矿柱变形趋势和破坏程度。

图9  矿柱破裂面实景图

Fig. 9  Fracture surface of pillar

图10  监测点水平位移曲线对比图

Fig. 10  Comparison chart of horizontal displacement curve

3  结论

1) 提出了基于动态强度折减法分析矿柱渐进失稳演变的方法，揭示了矿柱渐进失稳演变规律。随着循环动态折减计算，破损区首先出现在矿柱4个边角部位，逐渐向底部中心区域扩展，直至贯通整个矿柱。

2) 矿柱破损区演变过程划分为3个阶段，包括：稳定期、扩展期、突变期；随着计算步长增加，破损单元数量由缓慢增加、稳定增加到急剧扩展。

3) 与整体强度折减法相比，该方法克服了人为夸大破损区、出现不正常破损区的缺点，准确揭示了矿柱渐进破坏过程，客观描述了矿柱渐进失稳演变趋势和变形破坏程度。

4) 现场矿柱变形位移监测结果验证了动态强度折减法分析结果的正确性。动态强度折减法为研究矿柱失稳机理和稳定性评价提供了一种新的有效方法。

参考文献：

[1] WALLACE J W, ELWOOD K J, MASSONE L M. Investigation of the axial load capacity for lightly reinforced wall piers[J]. Journal of Structural Engineering, ASCE, 2008, 134(9): 1548-1557.

[2] 宋义敏, 杨小彬. 煤柱失稳破坏的变形场及能量演变试验研究[J]. 采矿与安全工程学报, 2013, 30(6): 822-827.

SONG Yimin, YANG Xiaobin. Evolution characteristics of deformation and energy fields during coal pillar instability[J]. Journal of Mining & Safety Engineering, 2013, 30(6): 822-827.

[3] 王学滨. 屈服矿柱渐进破坏及应力分布数值模拟[J]. 中国地质灾害与防治学报, 2006, 17(2): 50-56.

WANG Xuebin. Numercial simulation of progressive failure and stress distribution of yield pillars[J]. The Chinese Journal of Geological Hazard and Control, 2006, 17(2): 50-56.

[4] 刘增辉, 高谦. 两中段开采的水平矿柱失稳影响因素分析与方案优化: 以金川二矿区为例[J]. 中国安全科学学报, 2013, 23(11): 80-84.

LIU Zenghui, GAO Qian. Analysis of factors influencing horizontal pillar instability and optimization of two-level mining plans: taking Jinchuan No. 2 Mine as an example[J]. China Safety Science Journal, 2013, 23(11): 80-84.

[5] 马海涛, 谢芳. 大规模采空区渐进式矿柱坍塌的简化模拟[J]. 中国安全生产科学技术, 2013, 9(8): 17-21.

MA Haitao, XIE Fang. Simplified simulation on cascading pillar failure in large-scale goaf[J]. Journal of Safety Science and Technology, 2013, 9(8): 17-21.

[6] 林杭, 曹平, 赵延林, 等. 强度折减法在Hoek-Brown准则中的应用[J]. 中南大学学报(自然科学版), 2007, 38(6): 1219-1224.

LIN Hang, CAO Ping, ZHAO Yanlin, et al. The application of strength reduction method in Hoek-Brown criterion[J]. Journal of Central South University (Science and Technology), 2007, 38(6): 1219-1224.

[7] 陈国庆, 黄润秋, 周辉, 等. 边坡渐进破坏的动态强度折减法研究[J]. 岩土力学, 2013, 34(4): 1140-1146.

CHEN Guoqing, HUANG Runqiu, ZHOU Hui, et al. Research on progressive failure for slope using dynamic strength reduction method[J]. Rock and Soil Mechanics, 2013, 34(4): 1140-1146.

[8] 陈国庆, 黄润秋, 石豫川, 等. 基于动态和整体强度折减法的边坡稳定性分析[J]. 岩石力学与工程学报, 2014, 33(2): 243-256.

CHEN Guoqing, HUANG Runqiu, SHI Yuchuan, et al. Stability analysis of slope based on dynamic and whole strength reduction methods[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(2): 243-256.

[9] 杜丽惠, 黄丽清. 考虑围岩蠕变特性的轴对称有限元非线性分析[J]. 水利学报, 2001(1): 85-89.

DU Lihui, HUANG Liqing. The nonlinear axisymmetric finite element method for analysis of surrounding rock in consideration of creeping[J]. Journal of Hydraulic Engineering, 2001(1): 85-89.

[10] 周辉, 张传庆, 冯夏庭, 等. 隧道及地下工程围岩的屈服接近度分析[J]. 岩石力学与工程学报, 2005, 24(17): 3083-3087.

ZHUO Hui, ZHANG Chuanqing, FENG Xiating, et al. Analysis of rock mass stability in tunnel and underground engineering based on yield approach index[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(17): 3083-3087.

[11] ZHANG Chuanqing, ZHUO Hui, FENG Xiating. An index for estimating the stability of brittle surrounding rock mass：fai and its engineering application[J]. Rock Mechanics and Rock Engineering, 2011, 44(4): 401-414.

[12] DIEDERICHS M S, KAISER P K, EBERHARDT E. Damage initiation and propagation in hard rock during tunneling and the influence of Near-face stress rotation[J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(2): 785-812.

[13] 舒谷生, 彭文祥. 非线性准则下节理岩体稳定性的屈服接近度分析[J]. 中南大学学报(自然科学版), 2010, 41(5): 1883-1886.

SHU Gusheng, PENG Wenxiang. Yielding approach index analysis for stability of joint rock mass based on nonlinear criterion[J]. Journal of Central South University (Science and Technology), 2010, 41(5): 1883-1886.

[14] 王在泉, 李华峰. 矿柱抗剪安全系数的数值计算方法及分析[J]. 采矿与安全工程学报, 2010, 27(2): 277-280.

WANG Zaiquan, LI Huafeng. Numercial calculaition method for shear safty coefficient of mine pillar[J]. Journal of Mining & Safety Engineering, 2010, 27(2): 277-280.

[15] ZHENG H, LIU D F, LI C G. On the assessment of failure in slope stability analysis by the finite element method[J]. Rock Mechanics and Rock Engineering, 2008, 41: 629-639.

(编辑  杨幼平)

收稿日期：2015-02-13；修回日期：2015-04-20

基金项目(Foundation item)：“十二五”国家科技支撑计划项目(2012BAB08B02)；国家自然科学基金面上资助项目(51174093，51374035)(Project (2012BAB08B02) supported by the National Science and Technology Pillar Program during the 12th Five-Year Plan Period; Projects (51174093, 51374035) supported by the National Natural Science Foundation of China)

通信作者：吴爱祥，博士，教授，从事金属矿安全开采方面研究；E-mail：wuaixiang@126.com