J. Cent. South Univ. Technol. (2008) 15: 289-294

DOI: 10.1007/s11771-008-0054-3

Flow stress behavior of Al-Cu-Li-Zr alloy containing Sc during hot compression deformation

LIANG Wen-jie(梁文杰)^{1, 2}, PAN Qing-lin(潘清林)¹, HE Yun-bin(何运斌)¹,

LI Yun-chun(李运春)¹, ZHANG Xiao-gang(张小刚)¹

(1. School of Materials Science and Engineering, Central South University, Changsha 410083, China;

2. School of Chemistry and Chemical Engineering, Central South University,

Changsha 410083, China)

Abstract: The flow stress behavior of Al-3.5Cu-1.5Li-0.25(Sc+Zr) alloy during hot compression deformation was studied by isothermal compression test using Gleeble-1500 thermal-mechanical simulator. Compression tests were preformed in the temperature range of 653-773 K and in the strain rate range of 0.001-10 s^-1 up to a true plastic strain of 0.7. The results indicate that the flow stress of the alloy increases with increasing strain rate at a given temperature, and decreases with increasing temperature at a given imposed strain rate. The relationship between the flow stress and the strain rate and the temperature was derived by analyzing the experimental data. The flow stress is in a hyperbolic sine relationship with the strain rate, and in an Arrhenius relationship with the temperature, which imply that the process of plastic deformation at an elevated temperature for this material is thermally activated. The flow stress of the alloy during the elevated temperature deformation can be represented by a Zener-Hollomon parameter with the inclusion of the Arrhenius term. The values of n, α and A in the analytical expressions of flow stress σ are fitted to be 5.62, 0.019 MPa^-1 and 1.51×10¹⁶ s^-1, respectively. The hot deformation activation energy is 240.85 kJ/mol.

Key words: Al-Cu-Li-Zr alloy containing Sc; flow stress; hot compression deformation; Zener-Hollomon parameter

1 Introduction

The Al-Li alloys have been developed in recent years because of their distinct properties, such as high specific strength and low density. But they are characterized by low ductility and fracture toughness, which severely limit their commercial application. It is generally agreed that microalloying is one of the effective methods to improve the properties of Al-Li alloys^[1-5].

Sc is a special element, which has the lowest density in all of rare-earth elements and shows a similar nature to transition elements. Our previous research^[6] showed that addition of 0.1% Sc to Al-Cu-Li-Zr alloy can eliminate the dendrite of the alloy, and cause refinement of as-cast grain size, strongly restrain recrystallization of the alloy during hot rolling and solution treatment, and improve the strength and the ductility of the alloy. However, the behavior of high temperature deformation and the hot working processing parameter of Al-Cu-Li-Zr alloy containing Sc are still short of systematical researches. To examine the hot deformation behavior, the flow stress of materials at the elevated temperature is one of the indispensable information. During the hot deformation, the flow stress behavior is usually characterized by some factors such as strain rate, strain, deformation temperature and deformation activation energy^[7-10]. Equations expressing the flow stress as a function of strain, strain rate and temperature not only are useful to numerically analyze the hot deformation process, but also are most frequently used in engineering practice. For this reason, it is very important and necessary to investigate the behavior of plastic deformation of Al-Cu-Li-Zr alloy containing Sc at the elevated temperature.

In the present study, the flow stress of Al-Cu-Li-Zr alloy containing Sc was measured at various temperatures and strain rates, and the relationship between the flow stress and the strain rate and the temperature was analyzed based on experimental data, respectively.

2 Materials and experimental procedure

The raw materials were 99.8% Al, 99.9% Li and

Al-48.7%Cu, Al-2.23%Sc and Al-3.72%Zr master alloys. The alloy was prepared by weighing proper amounts of the constituent metals, melting them in a crucible furnace and pouring into a cast copper mold under argon protection. The composition of the alloy is Al-3.5%Cu- 1.5%Li-0.22%(Sc+Zr). After homogenization at 520 ℃ for 24 h, the cylindrical compression specimens were all machined from the ingot to 10 mm in diameter and 15 mm in height, as shown in Fig.1. Concentric annular grooves of 0.2 mm in depth were machined at both end faces of the cylinders to retain the lubricant during to the compression test. Graphite lubricant mixed with machine oil was used to minimize the friction between the sample and anvils.

Fig.1 Specimen of hot compression (unit: mm)

The specimens were pre-heated to compression temperature at a heating rate of 1 ℃/s and homogenized for 300 s before deformation. The hot compression tests were carried out on a Gleeble-1500 simulator. The deformation strain, the temperature and the strain rate were automatically controlled and recorded during hot deformation. Compression testing was conducted from 653 to 773 K in the strain rate range from 0.001 to 10 s^-1 up to a true plastic strain of 0.7.

3 Results and discussion

3.1 True stress—strain curves

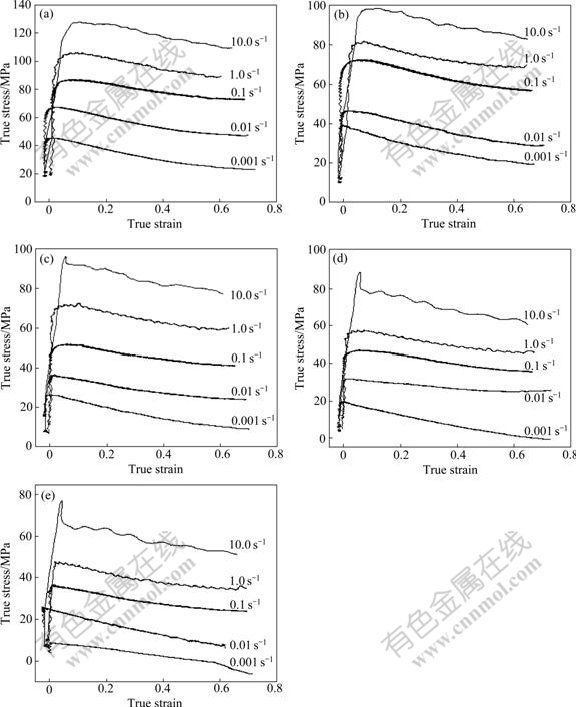
A series of true stress—strain curves obtained during hot compression of the alloy at various temperatures and strain rates are shown in Fig.2. It can be seen that the flow stress curves exhibit a remarkable peak stress at small strain (＜0.1). When the strain is less than the peak strain, the strain hardening plays the main role; when the strain surpasses the peak strain, the flow stress decreases with increasing strain. This indicates that the strain softening effect is larger than the strain hardening effect due to dynamic recrystallization. Fig.2 also shows that the flow stress increases with increasing strain rate under the condition of the same deformation temperature. During the deforming process at 743 K, for example, the peak flow stress increases from 22.30 to 58.43 MPa when the strain rate elevates from 0.001 to 1.0 s^-1, which shows that the studied alloy is a material with a positive strain rate sensitivity. And under the condition of the same strain rate, the flow stress decreases as the deformation temperature rises. Thus, the plastic flow behavior is seen to be thermally activated, and the flow stress be a strong function of temperature and strain rate.

3.2 Effect of strain rate on flow stress

During the hot deformation, the flow stress behavior of an alloy is usually characterized by some factors such as strain rate, strain and temperature. It is generally accepted that the relationship between the flow stress s, strain rate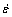 and temperature T can be expressed as^[11-13]

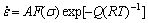                     (1)

There are three forms of the stress function F(σ) as follows:

F(σ)=σⁿ                                     (2)

F(σ)=exp(βσ)                                (3)

F(σ)=[sinh(ασ)]ⁿ                              (4)

where  A, n, α and β are all constants independent of temperature; α=β/n; R is the ideal gas constant, T is the absolute temperature; Q is the deformation activation energy, s is often taken as peak flow stress s_p or steady state stress. Eqns.(2) and (3) are usually given at low and high stress levels, respectively. The hyperbolic sine relationship (Eqn.(4)) covers all stress ranges.

Supposing that the relationship between s and 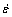 of the tested alloy could satisfy the relationships above, and assuming that Q is constant at a given temperature, then, at low and high stress levels, Eqn.(1) can be expressed as Eqns.(5) and (6), respectively.

                                   (5)

                              (6)

where  A₁ and A₂ are constants. After logarithms are taken from both sides, Eqns.(5) and (6) are respectively transformed into

                           (7)

                             (8)

According to Eqns.(7) and (8), and the flow stress is taken as peak flow stress, the results of the liner

Fig.2 True stress—strain curves for alloy at various temperatures and strain rates: (a) 653 K; (b) 683 K; (c) 713 K; (d) 743 K; (e) 773 K

  ­­­

regression analyses are shown in Fig.3. A linear relationship exists between 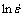 and lns with linear slope n, and a linear relationship exists between  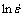and s with linear slope β. The average values of n and β are derived to be n=7.750 2 and β=0.147 1, respectively. Therefore, α value equals 0.019.

For all stress range, Eqn.(1) can be expressed as

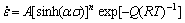               (9)

After logarithms are taken from both sides, Eqn.(9) is transformed into

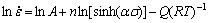           (10)

As shown in Fig.4, a linear relationship exists between 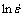 and ln[sinh(ασ)]. The values of the slope of five regressive curves at various temperatures are approached, and curves are almost parallel (Fig.4). It is indicated that Eqn.(9) is more appropriate than Eqns.(5) and (6), as shown in Figs.4 and 3. Therefore, it follows that the interrelation between flow stress and strain rate during hot deformation well satisfies the Arrhenius relationship of the hyperbolic sine form, which implies

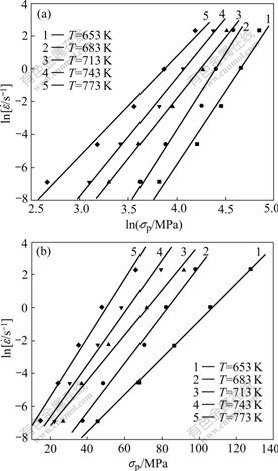
Fig.3 Relationship between strain rate and peak flow stress:  (a) —ln σ_p; (b) —σ_p

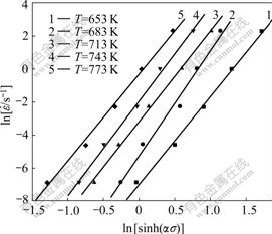
Fig.4 Linear relationship between  and ln[sinh(ασ)]

that the hot deformation process for the alloy also is thermally activated, similar to the high temperature creep of pure Al^[14].

3.3 Effect of deformation temperature on flow stress

It can be seen from Fig.2 that the flow stress at a given imposed strain rate depends on the temperature in a normal manner, decreasing with increasing the temperature. If 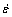 is constant, and Q is also constant in the range of experimental temperature, then, Eqn.(1) can be conveniently expressed in terms of a temperature compensated strain rate parameter, and the Zener- Hollomon parameter Z can be written as

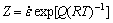                         (11)

The relationship between Zener-Hollomon parameter Z and flow stress s can be expressed as^[15]

Z=A[sinh(ασ)]ⁿ                              (12)

The substitution of Eqn.(11) into Eqn.(12) results in

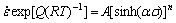                (13)

After logarithms are taken from both sides, Eqn.(13) is transformed into

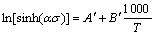                   (14)

where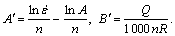

Fig.5 shows that the interrelation between peak flow stress σ_p and 1/T for the alloy during hot deformation well satisfies Eqn.(14). That is to say, the behavior of flow stress of the alloy during hot deformation can be described by Z parameter including Arrhenius term, and the process of hot deformation of the alloy is thermally activated.

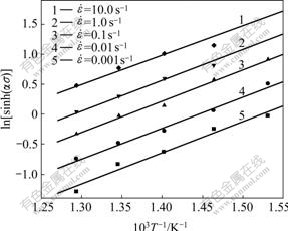
Fig.5 Linear relationship between ln[sinh(ασ)] and 1/T

3.4 Analytical expression of flow stress

The results from the above show that Eqn.(9) is even more adaptive to describe the flow stress behavior of the alloy. The deformation activation energy Q is calculated by using Eqn.(9) after differentiation at constant temperature and constant strain rate, and it is converted into the following form:

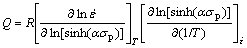     (15)

The two terms on the right of Eqn.(15) represent the slope of the 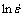—ln[sinh(ασ)] straight line at the employed temperature and the slope of ln[sinh(ασ)]—1/T straight line at the strain rate, respectively. According to Figs.4 and 5, the average slope values of the two relationships curves can be derived to be 5.669 4 and 5.112 3, respectively. Then, by substituting the two values into Eqn.(15), the average hot deformation activation energy Q is calculated to be 240.85 kJ/mol.

Substituting Q and the hot deformation condition into Eqn.(11), Z values are calculated. After logarithms are taken from both sides, Eqn.(12) is transformed into

ln Z=ln A+nln [sinh(ασ)]                       (16)

Then, taking ln [sinh(ασ)] and ln Z as the coordinates mapping, the results are shown in Fig.6. A linear relationship exists between ln Z and ln [sinh(ασ)]. It further demonstrates that the interrelationship between flow stress s and strain rate 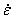, deformation temperature T for the alloy during hot deformation can be described by the Arrhenius relationship of the hyperbolic sine form, i.e. Eqn.(9), under the experimental condition. The slope of the straight line in Fig.6 is stress exponent n, the longitude intercept of lnA. The values of n and A are derived to be n=5.62 and A=1.51×10¹⁶ s^-1, respectively.

Fig.6 Linear relationship between ln Z and ln [sinh(ασ)]

The formula of flow stress is therefore determined to be

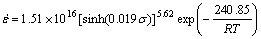   (17)

and its Zener-Hollomon parameter Z to be

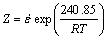                          (18)

According to Eqn.(12), the formula of flow stress can also be expressed by Zener-Hollomon parameter Z as follows:

(19)

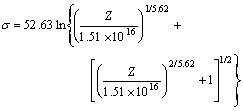
4 Conclusions

1) The flow stress is strongly dependent upon the temperature and the strain rate. Under the condition of the same deformation temperature, the true stress increases as the strain rate rises, and under the condition of the same strain rate, the true stress decreases as the deformation temperature rises.

2) The flow stress behavior of the alloy during hot deformation can be described by the Zener-Hollomon parameter Z including the Arrhenius term. The values of A, n, α in the analytical expression of flow stress s are fitted to be 1.51×10¹⁶ s^-1, 5.62 and 0.019 MPa^-1, respectively. The hot deformation activation energy of the alloy during hot deformation is 240.85 kJ/mol.

References

[1] GILMORE D L, STARKE E A Jr. Trace element effects on precipitation processes and mechanical properties in an Al-Cu-Li alloy [J]. Metall Mater Trans A, 1997, 28(7): 1399-1415.

[2] TAN Cheng-yu, ZHENG Zi-qiao, XIA Chang-qing, LIANG Ying. The aging feature of Al-Li-Cu-Zr alloy containing Sc [J]. J Cent South Univ Technol, 2000, 7(2): 65-67.

[3] ZHAO Zhi-long, LIU Lin, CHEN Zheng. Effect of rare earth cerium on yield strength anisotropy of Al-Li alloy sheet and its theoretical prediction [J]. J Rare Earth, 2004, 22(3): 410-413.

[4] BEREZINA A L, VOLKOV V A, IVANOV S V, KOLOONEV N I, CHUISTOV K V. The influence of scandium on the kinetics and morphology of decomposition of alloys of the Al-Li system [J]. Phys Met Metall, 1991, 71(2): 167-175.

[5] HUANG Lan-ping, ZHENG Zi-qiao, HUANG Yong-ping, ZHONG Li-ping. Effect of Sc on microstructure and mechanical properties of 2197 Al-Li alloy [J]. Journal of Central South University: Science and Technology, 2005, 36(1): 20-24. (in Chinese)

[6] LIANG Wen-jie, PAN Qing-lin, ZHU Zhao-ming, HE Yun-bin, LIU Yuan-fei, YIN Zhi-min. Effect of minor Sc on microstructure and tensile properties of Al-Cu-Li-Zr alloy [J]. Rare Metal Materials and Engineering, 2006, 35(4): 550-553. (in Chinese)

[7] FU G S, CHEN W Z, QIAN K W. Behavior of flow stress of aluminum sheets used for pressure can during compression at elevated temperature [J]. Acta Metallurgica Sinica: English Letters, 2005, 18(6): 756-762.

[8] ZHAN Mei-yan, CHEN Zhen-hua, ZHANG Hui, XIA Wei-yun. Flow stress behavior of porous FVS0812 aluminum alloy during hot- compression [J]. Mech Res Commun, 2006, 33: 508-514.

[9] ZHOU H T, ZENG X Q, WANG Q D, DING W J. A flow stress model for AZ61 magnesium alloy [J]. Acta Metallurgica Sinica: English Letters, 2004, 17(2): 155-160.

[10] SASTRY D H, PRASAD Y V R K, DEEVI S C. Influence of temperature and strain rate on the flow stress of an FeAl alloy [J]. Mater Sci Eng A, 2001, A299: 157-163.

[11] HAN Dong-feng, ZHENG Zi-qiao, JIANG Na, LI Jing-feng. Flow stress of high-strength weldable 2195 aluminum-lithium alloy during hot compression deformation [J]. The Chinese Journal of Nonferrous Metals, 2004, 14(12): 2090-2095. (in Chinese)

[12] SHEN Jian. Behavior of flow stress of 2091 Al-Li alloy during hot compression [J]. Chinese Journal of Rare Metals, 1998, 22(1): 47-50. (in Chinese)

[13] TAKUDA H, FUJIMOTO H, HATTA N. Modeling on flow stress of Mg-Al-Zn alloys at elevated temperatures [J]. J Mater Process Tech, 1998, 80/81: 513-516.

[14] RAYBOULD D, SHEPPARD T. Axisymmetric extrusion—The effect of temperature rise and strain rate on the activation enthalpy and material constants of some aluminum alloys and their relation to recrystallization, substructure and subsequent mechanical properties [J]. J Inst Metals, 1973, 101: 65-72.

[15] WANG Yu, LIN Dong-liang, LAW C C. A correlation between tensile flow stress and Zener-Hollomon factor in TiAl alloys at high temperatures [J]. Journal of Materials Science Letters, 2000, 19(13): 1185-1188.

(Edited by YANG Hua)

Foundation item: Project(2002AA305104) supported by the National High-Tech Research and Development Program of China

Received date: 2007-12-15; Accepted date: 2008-01-29

Corresponding author: LIANG Wen-jie, Doctoral candidate; Tel: +86-731-8830933; E-mail: wenjieliang1967@yahoo.com.cn