1万t多向模锻水压机分配器转角智能控制系统
喻寿益，汪少军，贺建军，桂卫华
(中南大学 信息科学与工程学院，湖南 长沙，410083)
摘 要：分析1万t多向模锻水压机分配器驱动系统的结构特点，提出一种智能超差二次调整控制算法。该算法应用神经网络控制和模糊控制对转角误差进行分段调整，由ε-NN神经网络输出提前量给开关伺服阀断电，采用模糊控制使伺服阀再次得电进行细调。仿真和实际应用结果表明，分配器能不振荡准确到位，转角误差由原来的-9?~9?变为-3?~3?；智能超差二次调整控制算法非常适用于含有带死区的继电特性环节的不确定性位置控制非线性系统，实现无振荡快速高精度位置控制。
关键词：模锻水压机分配器；转角跟踪；分段调整；智能控制
中图分类号：TM301.2 文献标识码：A 文章编号：1672-7207(2009)01-0175-05
Intelligent control system for angle of dispenser in ten-thousand-ton multidirectional die forging hydraulic press
YU Shou-yi, WANG Shao-jun, HE Jian-jun, GUI Wei-hua
(School of Information Science and Engineering, Central South University, Changsha 410083, China)
Abstract: The characteristic of driving system for the dispenser used in ten-thousand-ton multidirectional die forging hydraulic press was analyzed. An intelligent control algorithm of two-times regulation of angle error was proposed, which combined neural network control and fuzzy control. Advanced output of neural network control turns off the servo valve switch. Fuzzy control turns on the servo valve switch again for more precise regulation. The simulation and practical results demonstrate that dispenser can track reference angle value quickly and precisely without oscillation; the angle error is reduced from -9?—9? to -3?—3?; the proposed intelligent control algorithm is applicable to the uncertain nonlinear system with relay character element having dead zone for high-speed and high-precision position control without oscillation.
Key words: die forging hydraulic press dispenser; angle tracking; divided phases regulation; intelligent control
1万t多向模锻水压机是制备大型高强度铝合金构件的关键装备，这些构件(如飞机大梁、机翼龙骨和火箭导弹端环等)，是航空航天器的重要组成部分。其模锻加工过程由四大可移动工作部分按顺序协同动作完成，它们是垂直横梁，左、右水平部分和移动工作台，各部分的运动速度和行程由数字电液伺服系统控制[1]。四大可移动部分的运动分别由操作台上4个相应的手柄来操作，操作手柄可在0?~176? 移动，分别设置了“空程”、“工作”、“回程”和“停止”4个位置，它们对应一定的角度值，控制垂直方向和左右水平方向模锻加压过程的4个进程。当模锻工作时，扳动操作手柄到4个进程对应的位置，给出要求转动的角度，通过4组数字电液伺服系统分别带动垂直分配器，左、右水平分配器和移动工作台分配器转动。每个分配器轴上沿轴向安装有多个凸轮，由于凸轮的形状和安装位置不同，分配器转到设定的角度时，这些凸轮带动相应的顶杆上升或下降，从而控制相应的水阀，高压水进入不同工作缸驱动相应的移动工作部分完成要求的动作，实现模锻加压过程。
数字电液伺服系统采用开关伺服阀，它是带死区的继电器特性环节。由于水阀阻力矩具有明显的非线性和不确定性，而且分配器驱动系统的稳定裕量很小，近似非稳定对象，采用经典的PID控制和自适应控制都难以实现分配器无振荡快速准确到位[2]。本文作者将神经网络控制[3-4]和模糊控制[5]相结合，克服系统的非线性不确定性，提出智能超差二次调整控制算法，使分配器快速无振荡地转动到给定位置，提高控制精度。
1 分配器控制系统原理
垂直、左右水平和移动工作台3组数字电液伺服系统的组成基本相同，由绝对式光电编码器、现场控制器、液压驱动系统、分配器、水压系统和水压机组成，其原理示意图如图1所示。
图1 分配器转角控制系统原理示意图
Fig.1 Framework of dispensing equipment control system
操作台上的操作手柄转轴通过弹性连轴节与光电编码器OPT1相连发送分配器转角设定值。OPT2用弹性连轴节和分配器凸轮轴连接，测量分配器实际转动角度，编码器将操作手柄和分配器的转动角度转换成14位数字信号，通过profibus现场总线输入现场控制器。控制器将两个角度值进行比较，判断偏差的大小和方向，输出控制信号接通不同的电磁阀，使中压油进入接力器油缸推动分配器凸轮轴转动。直到OPT2与OPT1的角度偏差小于允许值为止，电磁阀断电，分配器便停在期望的位置上[6]。液压驱动系统由液压站、接力器和齿轮齿条变速装置组成，齿轮安装在分配器的凸轮轴上，驱动分配器凸轮轴旋转。液压驱动系统伺服阀为开关电磁阀[8]，由现场控制器输出开关信号控制，它们等效为带死区δ的继电器特性环节；阻力矩Mf是闸型水阀受高压水的压力产生的，随阀门开度和高压水压力变化，它是转角θ的非线性函数，具有不确定性，分配器数字电液伺服系统是有不确定性的Ⅱ型非线性系统，转动惯量J较大，稳定裕量很小，其系统原理如图2所示。减小角度跟踪误差?θ使分配器不产生振荡地快速准确到位难度很大，角度跟踪误差大使锻件欠压量大；若分配器转动产生振荡，会引起模锻过程压力曲线变化，使锻件内部织构变差。
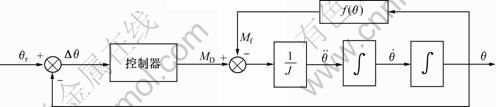
图2 数字电液伺服系统原理图
Fig.2 Digital electricity-liquid servo system
为了实现分配器转角快速无振荡达到设定值，减小角度跟踪误差，采用智能超差二次调整控制算法，它将人工神经网络控制和模糊控制相结合，对凸轮轴转角跟踪误差分段进行二次调整，其原理框图如图3所示。图中用神经网络ε-NN拟合计算出合适的提前量ε给伺服阀断电，分配器快速旋转到接近设定位置θr；由于驱动系统的惯性作用，分配器继续旋转一个角度；再判断?θ是否满足-δ＜?θ＜δ(δ为转角允许误差)，若不满足，则根据?θ的符号、高压水压力和要求的控制精度δ由模糊控制器计算出给相应伺服阀再次通电的时间τ，最终使分配器停在要求的控制精度-δ~δ范围内。
图3 分段调整位置控制系统原理框图
Fig.3 Divided phases regulation position control system
2 算法实现
分配器转动分为2个阶段：第1阶段为分配器快速向设定值转动阶段，采用人工神经网络控制，为“粗调”；第2阶段为模糊控制，为“微调”。
2.1 ε-NN算法
计算提前量ε的神经网络结构图如图4所示。输入层节点数m＝3个，分别为转角误差?θ及其变化率
和压力p，要进行归一化处理；由于训练时间受到生产实际情况的限制，隐含层节点数n＝5；输出层节点1个，输出为提前量ε。由于ε不能为负值，所以输出层神经元的活化函数取非负的Sigmoid函数，而隐含层神经元的活化函数为可取正负的Sigmoid函数。
图4 ε-NN结构示意图
Fig.4 Sketch map of ε-NN frame
ε-NN输入层的输入输出为：
隐含层的输入输出为：
式中：
为隐含层加权系数；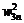
为阈值；活化函数
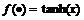，为超越正切函数；上角标1，2和3分别表示输入层、隐含层和输出层。
输出层的输入输出为：
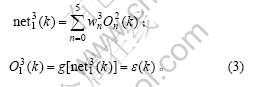
式中：
为输出层加权系数；
为阈值；活化函数
。
取性能指标函数为：
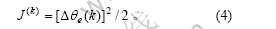
式中：
；
为开关电磁阀再接通时间τ后剩余误差
与δ的差。
依最速下降法修正网络的加权系数，并附加一项加速收敛全局极小的惯性项[8-9]，则有：
ε-NN算法网络训练采用离线和在线相结合的方法，在调试期间由现场控制器采集、和p，存储在计算机中，进行训练得到合适的提前量ε，再进行试运行，通过学习机制做合适的微调[10-11]。自学习算法由操作监控计算机在模锻过程中的2个进程之间的间隙时间(一般为3~10 s)内执行，并对算出的微调量进行判断，优化提前量ε。
2.2 模糊推理控制算法
系统模糊控制器的设计中，充分考虑专家经验，采用量化的方法建立三角形隶属度函数。通过经验归纳法建立IF…THEN…模糊控制规则；采用Mamdani模糊推理算法，进行似然推理；得到再次通电时间的模糊量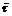
，解模糊后，得到再次通电时间τ。
根据系统控制精度的要求，转角跟踪误差?θ、压力p和再通电时间τ的模糊变量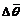
，
和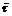都取为｛负大，负中，负小，零，正小，正中，正大｝，即｛NB，NM，NS，ZO，PS，PM，PB｝。其中，压力p事先设定一标准值，检测值和标准值的偏差除以标准值的比值再模糊化为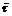；的ZO对应的再通电时间为0，N表示反转，p表示正转，经解模糊得到再通电时间τ。根据专家知识和操作人员经验积累，伺服阀再次通电时间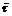的模糊推理规则如表1所示。
表1 模糊控制规则表
Table 1 Fuzzy control rules
用Matlab 7.0.1sp1[12-13]，按图3所示建立计算机仿真模型，仿真结果如图5所示。其中，转角设定值为90?阶跃信号，仿真时间根据实际系统运行情况选为5 s，水压分别是25，28和30 MPa，表明水压波动5 MPa，分配器仍然可以无振荡准确到位，控制精度为-3?~3?，达到设定值的时间小于2.5 s。在现场实际运行，监控画面显示分配器控制精度为-3?~3?，对于最大行程179?，准确到位时间不超过3 s。
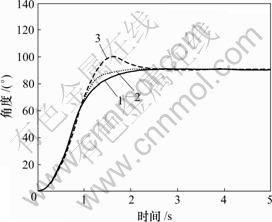
水压/MPa: 1—30; 2—28; 3—25
图5 智能控制系统的仿真结果曲线
Fig.5 Simulation results of intelligent control system
3 结 论
a. 1万t多向模锻水压机分配器驱动采用数字电液伺服系统，由于伺服阀为开关阀，驱动系统阻力矩是其转角的函数，包含带死区的继电器特性环节。采用非智能控制算法容易产生振荡，很难保证分配器不振荡准确到位，转角控制精度低。
b. 采用智能超差二次调整控制算法，由神经网络拟合的提前量给伺服阀断电，再进行适当的二次调整，保证了分配器不振荡快速到位。
c. ε-NN神经网络具有自学习功能，使提前量能补偿系统的非线性，按“专家经验”建立的模糊推理规则，对分配器凸轮轴转角误差做微调，保证了二次调整的控制精度，系统转角误差由原来的-9?~9?变为 -3?~3?。
d. 智能超差二次调整控制策略对于包含继电特性环节的不确定性非线性位置控制系统可以实现快速高精度控制。
参考文献：
[1] 关景泰. 机电液控制技术[M]. 上海: 同济大学出版社, 2003: 67-102.
GUAN Jing-tai. Electro-hydraulic control technology[M]. Shanghai: Tongji University Press, 2003: 67-102.
[2] 高为炳. 非线性控制系统导论[M]. 北京: 科学出版社, 1988: 30-53.
GAO Wei-bing. Nonlinear control system global context[M]. Beijing: Science Press, 1988: 30-53.
[3] 刘国栋. 用神经网络辨识非线性大滞后系统的研究[J]. 信息与控制, 2000, 29(3): 225-229.
LIU Guo-dong. A study of how to identify nonlinear macrohysteretic system by means of nerve network[J]. Information and Control, 2000, 29(3): 225-229.
[4] 罗建斌. 基于人工神经网络的锻压停止位控制研究[J]. 清华大学出版社, 1995, 35(2): 70-75.
LUO Jian-bin. Study on stop position control of a hydraulic press using artificial neural network[J]. Journal of Tsinghua University, 1995, 35(2): 70-75.
[5] 喻寿益, 王吉林, 彭晓波. 基于神经网络的铜闪速熔炼过程工艺参数预测模型[J]. 中南大学学报, 2007, 38(3): 523-527.
YU Shou-yi, WANG Ji-lin, PENG Xiao-bo. Prediction model of craft parameters based on neural network during the process of copper flash smelting[J]. Journal of Central South University: Science and Technology, 2007, 38(3): 523-527
[6] 张国良, 曾 静, 柯熙政. 模糊控制及其MATLAB应用[M]. 西安: 西安交通大学出版社, 2002: 21-40.
ZHANG Guo-liang, ZEN Jing, KE Xi-zheng. Fuzzy control and the application of MATLAB[M]. Xi’an: Xi’an Jiaotong University Press, 2002: 21-40.
[7] 逢振旭, 李从心, 倪其民. 液压计算机控制与监测系统的设计[J]. 计算机应用, 2000, 20(9): 54-56.
FENG Zhen-xu, LI Cong-xin, NI Qi-min. Hydraulic press computer control and the design of monitor module[J]. Computer Application, 2000, 20(9): 54-56.
[8] 丛 爽. 典型人工神经网络的结构、功能及其在智能系统中的应用[J]. 信息与控制, 2001, 30(2): 97-103.
CONG Shuang. A survey of structures, functions of artificial neural networks and their applications in intelligent systems[J]. Information and Control, 2001, 30(2): 97-103.
[9] 丛 爽, 向 微. BP网络结构、参数及训练方法的设计与选择[J]. 计算机工程, 2001, 27(10): 36-38.
CONG Shuang; XIANG Wei. Design and selection of construction, parameters and training method of BP network[J]. Computer Engineering, 2001, 27(10): 36-38.
[10] TIAN Qi-chuan. Research on learning algorithm of BP neural network based on the metropolis criterion[J]. Control Theory and Applications, 2003(5): 15-17.
[11] 高 隽. 人工神经网络原理及仿真实例[M]. 北京: 机械工业出版社, 2003: 10-35.
GAO Juan. Artificial neural networks theory and simulinkexamples[M]. Beijing: China Machine Press, 2003: 10-35.
[12] 黄文梅, 杨 勇, 熊桂林, 等. 系统仿真分析与设计- MATLAB语言工程应用[M]. 长沙: 国防科技大学出版社, 2001: 15-46.
HUANG Wei-mei, YANG Yong, XIONG Gui-lin, et al. System simulink analysis and design-MATLAB program engineering application[M]. Changsha: National University of Defense Technology Press, 2001: 15-46.
[13] 飞思科技产品研发中心. MATLAB7辅助控制系统设计与仿真[M]. 北京: 电子工业出版社, 2005: 53-70.
Feisi Production Research Center. MATLAB7 assistant control system design and simulink[M]. Beijing: Electronic Industry Press, 2005: 53-70.
收稿日期：2008-03-10；修回日期：2008-05-08
基金项目：国家自然科学基金资助项目(60574030)
通信作者：喻寿益(1940-)，男，江西南昌人，教授，博士生导师，从事自适应控制、人工智能等研究；电话：0731-8836739；E-mail: s-yushouyi@sina.com
