J. Cent. South Univ. Technol. (2007)05-0679-06
DOI: 10.1007/s11771-007-0130-0 
Dynamic modeling and simulation for
nonholonomic welding mobile robot
ZHANG Ke(张 轲)1, WU Yi-xiong(吴毅雄)1, L? Xue-qin(吕学勤)2, JIN Xin(金 鑫)1
(1. School of Materials Science and Engineering, Shanghai Jiaotong University, Shanghai 200030, China;
2. Faculty of Electric and Automatic Engineering, Shanghai University of Electric Power, Shanghai 200090, China)
Abstract：Based on the Newton-Euler method, the dynamic behaviors of the left and right driving wheels and the robot body for the welding mobile robot were derived. In order to realize the combination control of body turning and slider adjustment, the dynamic behaviors of sliders were also investigated. As a result, a systematic and complete dynamic model for the welding mobile robot was constructed. In order to verify the effectiveness of the above model, a sliding mode tracking control method was proposed and simulated, the lateral error stabilizes between -0.2 mm and +0.2 mm, and the total distance of travel for the slider is consistently within ±2 mm. The simulation results verify the effectiveness of the established dynamic model and also show that the seam tracking controller based on the dynamic model has excellent performance in terms of stability and robustness. Furthermore, the model is found to be very suitable for practical applications of the welding mobile robot.
Key words: dynamic model; seam tracking; sliding mode control; welding mobile robot
1 Introduction
Research on a welding mobile robot that is suitable for specially non-structured working environments has gained increasing attention. Examples of which are the spherical tank all-position welding mobile robot based on two linear charge coupled device(CCD) sensors[1-2], a crawling welding machine based on structured light for a storage tank or oil pipeline welding[3], the wheeled welding robot for welding in the lattice region of egg boxes inside the ship bottom[4], the intelligent welding mobile robot for ship deck welding that has the function of auto-searching weld line[5-6], and so on[7-9].
In real welding environments, however, due to the external disturbance or the perturbation of structural parameters, such as actual vehicle dynamic inertia and the power limits of actuators and localization errors, the method of the linear control theory based on the kinematics model could not result in good performance[9], especially in the aspects of the stability and robustness. Therefore, in order to address this problem, nonlinear controls such as sliding mode control are employed for a welding mobile robot[10-11].
Through there are much research on tracking control based on the dynamic model for the nonholonomic constraints mobile robot[10-14], there have been relatively few studies on seam tracking control in practice[8]. In this study, therefore a dynamic model for nonholomic welding mobile robot was established systematically and completely. In order to verify the effectiveness of the tracking control method based on the dynamic model, a new sliding mode seam tracking control method was correspondingly proposed and simulated.
2 Kinematic constraint equations
The developed welding mobile robot[5,15], which has two independent driving wheels and two free casters, is a 2-DOF(degree of free) vehicle moving on a flat plane. Its structure is shown in Fig.1. Oxy is a global coordinate system, and Ex′y′ is a local coordinate frame attached to the mobile robot with origin E, which is the midpoint of the axis line of two driving wheels, where point C denotes the center of mass for the welding mobile robot, point T is the center position of the cross slider, point F represents the position of the welding torch and sensor, and r denotes the radius of the driving wheel. The posture and velocity of point E represent the posture and velocity of the robot, (x, y) indicates the position of the robot guide point E, and θ is the heading angle of the robot relative to the x axis. 2c denotes the distance between the left and right driving wheels, a denotes the distance between the guide point E and the center point T of the cross slider, d represents the distance between the
center of mass point C and the guide point E, and b represents the distance between the welding torch point F and the center point T of the cross slider.
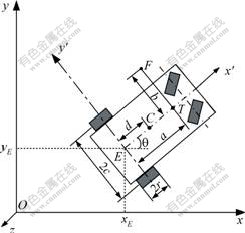
Fig.1 Structure of developed welding mobile robot
Let v and ω denote the linear and angular velocity, respectively, and the kinematic model of the mobile robot body can be described by a Jacobian matrix J as follows[16]:
Let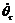 
and 
denote the angular velocities of the right and left driving wheels, respectively. From the Eqn., three constraints can be obtained as follows:
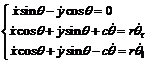
Eqn.(2) corresponds to the hypothesis of pure rolling and non-slipping condition, and shows that the mobile robot is a typical nonlinear dynamic system with the above nonholonomic constraints.
3 Dynamic modeling
From Fig.1, it can be seen that the developed welding mobile robot can be divided into three parts: the left and right driving wheels, the vehicle frame, and the slider adjustment device[17].
3.1 Left and right driving wheels
When in the condition of pure rolling without any slipping, the relationship between the linear velocities vl, vr and the angular velocities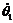 
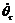, can be described as follows:
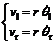
Let Be be the effective viscous friction coefficient of the combined motor rotor, gearbox, and wheel. The dynamic equation of the wheel motor assembly can be described as follows[18]:
where Iw is the effective moment of inertia, τ1 and τr are the driving torques of the left and right motors, respectively, Fl and Fr denote the left and right driving forces, respectively, and θi (i =r, l) is the rotational angle of the driving wheels.
3.2 Vehicle frame
The dynamic analysis of the welding mobile robot body is shown in Fig.2. The Newton-Euler equations of the vehicle frame are expressed as follows:
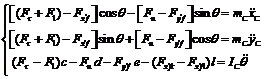
where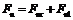 
，
,
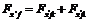, (xc, yc, θ)T denotes the posture of the center of mass with respect to the global coordinates, mC is the vehicle frame mass, IC is the frame inertia relative to point C, Fx'fr, Fx'fl, Fy'fr, and Fy'fl are the reaction forces applied on the frame by the front wheel, respectively, and Fnr and Fnl are the forces resulting from the normal friction forces between the ground and the wheel, respectively, 2l denotes the distance between the left and right front wheels, and e denotes the distance from the front wheel to the mass center C. Other structural parameters are shown in Fig.1.
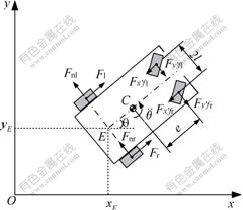
Fig.2 Dynamic analysis of welding mobile robot body
Point C is not the point to be tracked in order to obtain the dynamic description of welding torch point F. According to the plane motion principle of a rigid body, the geometrical relation between points C and F can be described as follows:
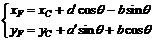
where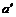 
denotes the distance from the slider center point T to the center of mass C. From Fig.1, 
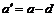can be derived.
For the differentially steered wheeled welding mobile robot, the relation among the linear velocities vl and vr of the driving wheels, the linear velocity v of the guide point E, and the angular velocity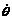 
can be described as follows:
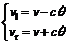
3.3 Cross slider
Let cb be the effective viscous friction coefficient of the combined motor and horizontal slider, and cz is that of the combined motor and vertical slider. Applying Newton’s Second Law to the horizontal and vertical sliders, the dynamic equations of the slider motor assembly can be described as follows:
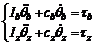
where ?θb and θz are the rotational angles of the stepping motors, respectively, Ib and Iz are the effective moments of inertia of the horizontal slider device and vertical slider device, respectively, and τb and τz denote the driving torques of the horizontal and vertical slider, respectively.
Since the cross slider is driven by two stepping motors through guide screws, let kb and kz be the thread intervals of the guide screws, respectively, then the linear velocities of the horizontal and vertical slider are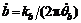 
and 
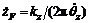respectively. The corresponding linear accelerations are 
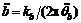and 
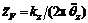, respectively. So the equation can be obtained as follows:
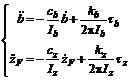
Finally, according to dynamic Eqns., , and , in combination with kinematic Eqn., and through transformation Eqns., , and , the dynamic model of the welding mobile robot can be described in vector form as follows:
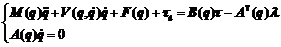
where q denotes the posture vector for welding torch point F, namely, q =[xF, yF, zF, θ, b]T, and τ denotes the torque input for the four driving motor, namely, τ= [τr, τl, τz, τb]T, τd presents the unknown disturbance and modeling dynamics,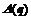 
is the Jacobian full rank matrix, 
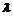denotes the vector of Lagrange multiplier that expresses the constraints forces in Eqn., and
describes the nonholonomic kinematic constraints of the welding mobile robot.
,
,
,
,
,
.
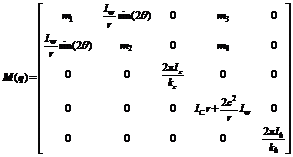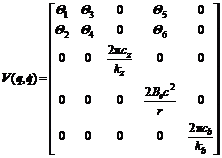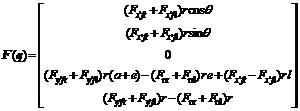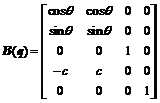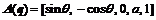where
，
,
,
,
，
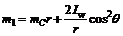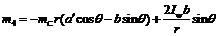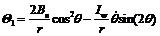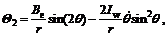
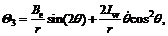
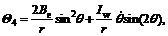
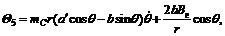
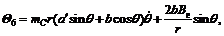
Eqn. is a full dynamic model for the developed welding mobile robot, and it completely and accurately describes the synthetic dynamic behavior involved when the four control motors of the robot body and cross slider act on the welding torch point F. This lays the foundation for the design of a robust seam tracking controller based on a dynamic model with uncertainties.
4 Dynamic simulation 4.1 Sliding mode seam tracking control based on dynamic model
In order to verify the effectiveness of the seam tracking based on dynamic modeling, a sliding mode control method was proposed.
According to the nonholonomic kinematic constraints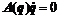
, choosing a full-rank matrix 
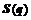, the following relation can be obtained:
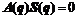
Considering the perturbation of the system parameter for welding mobile robot, let Δr, Δm, and ΔI present the absolute perturbation of the radius of the driving wheels r, mass m, and inertia I, respectively, then
, 
, 
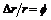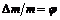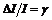
where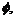 
φ and γ present the relative bounded disturbance, respectively.
Substituting Eqn. into Eqn. and carrying out input-output decoupling, the dynamic equation of the welding mobile robot is transformed into the following:
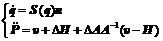
where u is a new control input, and H, A, ΔA, and ΔA are the parameter matrices that relate to system structure and dynamic performance.
Define the real welding torch posture P(xF, yF, θ) as output, Pd corresponds to the desired welding torch posture, and then the sliding surface s is defined as follows:
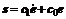
where c1 = 1 and c0 forms the equation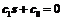 
with a negative real-part, tracking posture error 
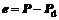, the velocity error 
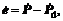and the variable structure control law is formed as follows:
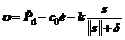
where k is the time-varying control gain and k＞0. It can enhance the anti-interference ability, eliminate the static error, and guarantee the existence of the sliding mode when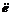 
and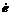 
are equal to zero.
According to the reachability of the sliding surface,
When the uncertain external disturbance factor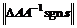 
＜1, the existence condition of the sliding surface can be satisfied, and k is as follows:
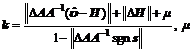＞0
Supposing that all the system state parameters can be measured, the sliding mode controller can be obtained as follows:
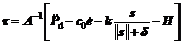
Fig.3 shows the schematic diagram of seam tracking based on sliding mode control for the welding mobile robot.
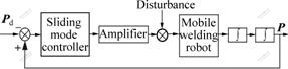
Fig.3 Seam tracking diagram of sliding mode control based on dynamic model with uncertainties
4.2 Simulation and experiment
In order to verify the effectiveness of the proposed method for a welding mobile robot, the simulation for tracking a desired circle trajectory was performed based on Matlab software platform.
The conditions simulated were as follows. The desired linear velocity, angular velocity, and control sampling period were 20 mm/s, 0.02 rad/s, and 0.2 s, respectively. The initial posture for the mobile welding robot was (0, 1 000, 1?), and the structure parameters for the welding mobile robot were a=390 mm, b=192 mm, c=117 mm, and r=50 mm. These parameters were completely consistent with those of the developed mobile welding robot[17]. Then the design parameters of the sliding surface were c1=1, c0=4, and μ=1, respectively, while the disturbance was chosen to be Gaussian random noise with mean value of 0. The variance of the parameters’ perturbation of the radius of driving wheels r, inertia I, and mass m was 0.5 mm, 0.3 N?m and 2 kg, respectively. The simulation results are shown in Figs.4, 5, and 6.
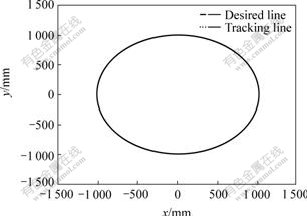
Fig.4 Tracking circle based on sliding mode control on basis of dynamic model
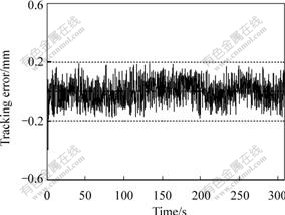
Fig.5 Lateral error during tracking of circle
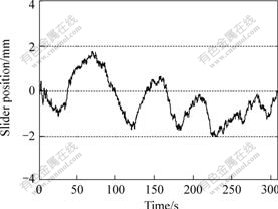
Fig.6 Lateral slider position during tracking of circle
Fig.5 shows the lateral error that consistently stabilizes between -0.2 and 0.2 mm. Meanwhile, Fig.6 shows that at the beginning of seam tracking, the slider position shows a bigger change and then gradually goes to steady state, but the total distance of travel for the slider is consistently within ±2 mm. Furthermore, from Figs.5 and 6, it can be seen that although the random parameters perturbation is applied to the system, the tracking error remains within the small boundary. Overall, the simulation results for seam tracking show that the control law based on the dynamics can obtain good performance in terms of stability and tracking accuracy.
5 Conclusions
1) The dynamic model for the developed welding mobile robot is established. As a result, the foundation for the design of a robust seam tracking controller based on a dynamic model with uncertainties is laid.
2) The dynamic model established completely and accurately describes the dynamic behaviors involved when the four control motors, namely, the motors for the left and right driving wheel, and the motors for the horizontal and vertical slider, act on the weld torching point.
3) A sliding mode tracking control method for the welding mobile robot is proposed. The simulation results verify the effectiveness of the established dynamic model, and they also show that the seam tracking controller based on a dynamic model has excellent performance in terms of stability and robustness. Therefore, this model is proven to be suitable for practical applications of the welding mobile robot.
References
[1] JIANG Li-pei, JIAO Xiang-dong, XUE Li, et al. Key points of high efficient automatic welding technique for large scale spherical steel tank[J]. Chinese Journal of Mechanical Engineering, 2003, 39(8): 146-150. (in Chinese)
[2] WANG Jun-bo, SUN Zheng-guo, CHEN Qiang. Intelligent wheeled mobile robot for spherical tank welding[C]//SPIE. Mobile Robots XVI. Boston, MA, USA, 2001, 4573: 244-255.
[3] ZHANG Hua, WANG Hai-dong, XUE Jia-nin, et al. A new wheeled autonomous mobile welding robot system based on rotating arc sensor[J]. Robot, 2003, 25(6): 536-540. (in Chinese)
[4] KAM B O, JEON Y B, KIM S B. Motion control of two wheeled welding mobile robot with seam tracking sensor[C]//IEEE International Symposium on Industrial Electronics. Pusan, South Korea, 2001: 850-856.
[5] ZHANG Ke, L? Xue-qin, WU Yi-xiong．Study on welding mobile robot with the function of auto-searching welding line[J]. China Welding, 2006, 15(1): 68-69.
[6] ZHANG Ke, WU Yi-xiong, L? Xue-qin, et al. Trajectory planning of posture adjustment of welding mobile robot during auto-searching weld line[J]. Chinese Journal of Mechanical Engineering, 2005, 41(5): 215-220. (in Chinese)
[7] SUGA Y, MUTO A, KUMAGAI M. Automatic tracking of welding line by autonomous mobile robot for welding of plates (Tracking of linear and angled welding lines)[J]. Transactions of the Japan Society of Mechanical Engineers(Part C), 1997, 63(612): 2918-2924.
[8] JEON Y B, KAM B O, PARK S S. Seam tracking and welding speed control of mobile robot for lattice type welding[C]// IEEE International Symposium on Industrial Electronics. Pusan, South Korea, 2001: 857-862.
[9] SUGA Y, SATTO K, SANO T, et al. Recognition and automatic tracking of weld line in welding of T-joint of pipes by an autonomous mobile robot with vision sensor[J]. Transactions of the Japan Society of Mechanical Engineers(Part C), 1996, 62(595): 1191-1196.
[10] CHWA D. Sliding mode tracking control of nonholonomic wheeled mobile robots in polar coordinates[J]. IEEE Transaction on Control System Technology, 2004, 12(4): 637-644.
[11] YANG J M, KIM J H. Sliding mode control for trajectory tracking of nonholonomic wheeled mobile robots[J]. IEEE Transactions on Robotics and Automation, 1999, 15(3): 578-587.
[12] CHWA D, SEO J H, KIM P, et al. Sliding mode tracking control of nonholonomic wheeled mobile robots[C]//IEEE Proceeding of the American Control Conference. Anchorage, AK, 2002: 3991-3996.
[13] ZOU Xiao-bing, CAI Zi-xing, SUN Guo-rong. Design of lateral controller based on variable structure for a mobile robot[J]. Journal of Central South University of Technology: Natural Science, 2004, 35(2): 262-267. (in Chinese)
[14] ZHANG Y L, CHUNG J H, VELINSKY S A. Variable structure control of a differentially steered wheeled mobile robot[J]. Journal of Intelligent anf Robotic Systems, 2003, 36(3): 301-314.
[15] ZHANG Ke, L? Xue-qin, WU Yi-xiong, et al. Algorithm and implementation of auto-searching weld line for welding mobile robot[J]. Chinese Journal of Mechanical Engineering, 2006, 19(2): 176-180.
[16] KANAYAMA Y, KIMURA Y, MIYAZAKI F, et al. A stable tracking control method for a non-holonomic mobile robot[C]//IEEE International Workshop Intelligent Robot and systems. Osaka, Japan, 1991: 1236-1241.
[17] ZHANG Ke. Auto-searching weld line and intelligent control of real-time seam tracking for welding mobile robot[D]. Shanghai: Shanghai Jiaotong University, 2005. (in Chinese)
[18] DENG Z P, BRADY M. Dynamic tracking of a wheeled mobile robot[C]// IEEEInternational Conference on Intelligent Robots and Systems. Yokohama, Japan, 2002: 26-30.
Foundation item: Project(50605044) supported by the National Natural Science Foundation of China; Project(2004DFA02400) supported by the Key International Science and Technology Cooperation Program
Received date: 2007-03-10; Accepted date: 2007-04-28
Corresponding author: ZHANG Ke, PhD; Tel: +86-21-62933401; E-mail: zhangke@sjtu.edu.
(Edited by CHEN Wei-ping)
