J. Cent. South Univ. Technol. (2011) 18: 499-503
DOI: 10.1007/s11771-011-0723-5
Schedule algorithm for mitigating inter-cell interference based on orthogonal complement space
FU Shao-zhong(付少忠), GE Jian-hua(葛建华)
State Key Laboratory of Integrated Service Networks, Xidian University, Xi’an 710071, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2011
Abstract: In order to avoid severe performance degradation led by the inter-cell interference (ICI) in orthogonal frequency division multiple access (OFDMA) systems with a frequency reused factor (FRF) of 1, distributed schedule algorithm (DS-OCS) and distributed proportional fairness schedule algorithm (DPFS-OCS) based on orthogonal complement space (OCS) were proposed. The first right and left singular vectors of the channel that the user experienced were selected as the transmitting and receiving beamforming vectors. An interference space was spanned by the left singular vectors of the entire interference users in the same channel. The most suitable user lay in the OCS of the interference space was scheduled to avoid suffering interference from neighboring cells based on the criterion of system capacity maximizing and proportional fairness. The simulation results show that the average system capacity can be improved by 2%-4% compared with the DS-OCS algorithm with the Max C/I algorithm, by 6%-10% compared with the DPFS-OCS algorithm with the PF algorithm.
Key words: long term evolution; interference avoidance; schedule algorithm; orthogonal complement space; fairness
1 Introduction
With the rapid development of wireless communication, the effective use of limited resource has become more and more important. The lack of wireless resource is the major bottleneck, so the frequency reused factor approaches 1 rather than 3 to improve the resource utilization rate. By adopting orthogonal frequency division multiple access, the inter-carrier interference and intra-cell interference can be almost avoided since data streams for different subscribers are conveyed on different subcarriers that are orthogonal to each other. But, severe inter-cell interference can be engendered because the users in all cells use the same frequency resource, which will significantly deteriorate the system throughput.
The existing inter-cell interference suppressing techniques can be divided into three catalogs: inter-cell interference coordination, inter-cell interference randomization, and inter-cell interference cancellation.
In Ref.[1], a specific pseudo noise or interleaving scheme is assigned to each cell. The interference from neighboring cell behaves as an additive white Gaussian noise after descrambling or deinterleaving by the subscribers. Although the 3rd generation partnership project (3GPP) has adopted 504 pseudo noises to mitigate the inter-cell interference of long term evolution (LTE), the randomization technique cannot reduce the power of the interference. The interference is mitigated by the process gain at the subscribers.
The inter-cell interference cancellation algorithm proposed in Ref.[1] reconstructs the interference and removes the interference from the received signal. The residual signal is composed of the desired signal and noise. If the interference can be rebuilt accurately, this scheme is an efficient interference elimination algorithm. But, up to now, it is difficult to rebuild the interference exactly.
Interference coordination is the most widely used method. The emergence of orthogonal frequency division multiple access (OFDMA) triggered the investigations on interference coordination techniques [2-8]. The soft frequency reuse (SFR) algorithm has been proposed in Ref.[2], where FRF of 1 is adopted in cell center whereas the FRF is 3 or more at cell edge. The subscribers at the edge of neighboring cells use different frequency bands, which effectively suppresses the inter-cell interference. However, the subscribers at the edge of cells can use only a fraction of entire frequency bands, resulting in a performance loss in frequency selective schedule gains and peak data rates. On the other hand, the gain of the SFR comes from the downlink power control. 3GPP approved no power control. Thus, SFR cannot be applied to LTE.
YOSIA and LARS [9] have proposed a block- diagonalization technique that makes use of a linear precoding matrix to transmit multiple data streams to each user while removes the inter-cell interference at the same time. However, the algorithm needs base station (BS) coordination, which leads to high complexity and relatively low efficiency. As an available technique, frequency hopping technique was adopted in Ref.[10] to alleviate the inter-cell interference, but it suffers from difficulty in frequency hopping pattern design.
By the extension of the proportion fairness (PF) schedule to static power reuse scheme in Ref.[11], a softer frequency reuse (SerFR) scheme is proposed in Ref.[12]. In the SerFR scheme, the FRF at the cell center and at the cell edge are both one. Frequency band is divided into three segments: two low power frequency bands and one high power frequency band. The high power frequency band is different from the neighboring cells. The fixed high power frequency band is deducted from the FRF 3, decreasing the frequency utilization rate, so the system throughput is limited. The gain of the SerFR also comes from the downlink power control. For the same reason as the SFR, SerFR cannot be applied to LTE either.
Beamforming is a popular technique for the mitigation of the interference [13-15]. Beamforming focuses its transmission or reception in the direction of a particular subscriber, and the interference to or from the subscribers in other directions is minimized.
In this work, the OFDMA system with a FRF of 1 is studied. The beamforming vector based on the channel feedback by the subscriber is derived. An interference space is spanned according to the interference channels. Then, distributed schedule algorithm (DS-OCS) and distributed proportional fairness schedule (DPFS-OCS) algorithm based on orthogonal complement space of interference space are proposed.
2 System model analysis
A cellular system based on orthogonal frequency division multiplexing (OFDM) scheme is studied. The FRF is 1, and OFDMA is adopted. The cellular layout is composed of M hexagonal grid cells with three sectors per cell. There are 3M sectors totally. The base station is resided in the center of the cell. The transmit antennas is Nt per sector. Let Ui (i=1, …, 3M) be the subscribers set of sector i. Each subscriber equips Nr receiving antennas and only accepts service from the base station (BS) where the user is located. A group of successive n subcarriers that experience similar fading are collected to form a subchannel in order to reduce the control information while keeping system performance unchanged. Subchannel is the minimum schedule unit in resource distribution. The transmit power assigned to each subchannel is the same. Each subchannel can be allocated to only one subscriber at one schedule period. The subscribers who use the same subchannel in different sectors are co-channel subscribers. It is clear that co-channel subscribers in neighboring sectors suffer interference from each other. Finally, it is supposed that the channels from all BSs to any subscriber could be perfectly estimated and fed back to the service BS without delay.
The subscriber on subchannel c in sector k may receive signal from all 3M sectors. The received signal could be modeled as
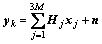 (1)
(1)
where yk is the complex received signal with the dimension of Nr×1. The matrix Hj is the Nr×Nt transfer channel from the j-th sector. Hj is the interference channel when j≠k. n is the vector of additive white Gaussian noise (AWGN) experienced by the subscriber such that its expectation value 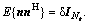 The vector xj is the complex signal destined to the subscriber from the j-th sector with the dimension of Nt×1.
The vector xj is the complex signal destined to the subscriber from the j-th sector with the dimension of Nt×1.
If dj is the datum intended to transmit in the j-th cell, and wj is the beamforming vector, then xj=wjdj. Performing singular value decomposition (SVD) of Hj in Eq.(1) yields Hj=UjΛjVj, where Uj is the left unitary matrix, Vj is the right unitary matrix and Λj is the diagonal matrix. Let  be the first eigenvalue of Hj, which is much larger than the other eigenvalues in the outdoor scenario, so transmitting a single data stream on the first eigenvalue channel will not degrade the system throughput too much. Then, the right singular vector
be the first eigenvalue of Hj, which is much larger than the other eigenvalues in the outdoor scenario, so transmitting a single data stream on the first eigenvalue channel will not degrade the system throughput too much. Then, the right singular vector 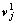 corresponding to
corresponding to 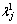 is selected as the beamforming vector
is selected as the beamforming vector 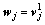 . Hence, the signal arriving at the subscriber in sector k can also be expressed as
. Hence, the signal arriving at the subscriber in sector k can also be expressed as
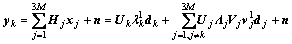 (2)
(2)
Since 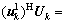 diag[1, 0], where 0 is a zero matrix of (Nr-1)×(Nt-1),
diag[1, 0], where 0 is a zero matrix of (Nr-1)×(Nt-1),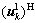 is selected as the receiving beamforming vector. The received signal at sector k could be expressed as
is selected as the receiving beamforming vector. The received signal at sector k could be expressed as
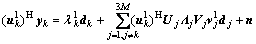 (3)
(3)
where the first item of the right hand of Eq.(3) is the desired signal at sector k, and the second item is the cochannel interference. Generally, 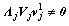 and therefore only
and therefore only 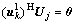 held could cancel the cochannel interference. Since the first eigenvalue is much larger than the other eigenvalues, we could just take the left singular vector
held could cancel the cochannel interference. Since the first eigenvalue is much larger than the other eigenvalues, we could just take the left singular vector 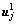 corresponding to the first eigenvalue into account; so the cochannel interference could be neglected when
corresponding to the first eigenvalue into account; so the cochannel interference could be neglected when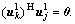
3 Orthogonal complement space based interference mitigation algorithm
Eq.(3) shows that the subscriber should be
scheduled to let 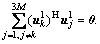 Therefore, inter-cell
Therefore, inter-cell
interference mitigation based on orthogonal schedule could be described as: scheduling the subscriber in Uk whose left singular vector is orthogonal to all (3M-1) co-channel subscribers, and simultaneously maximizing the eigenvalue.
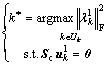 (4)
(4)
where 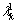 is the first eigenvalue of the channel from sector k to subscriber on the Subchannel c.
is the first eigenvalue of the channel from sector k to subscriber on the Subchannel c. 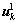 is the corresponding left singular vector.
is the corresponding left singular vector.
The left singular vector of (3M-1) interferences channel on Subchannel c forms the interference left singular vector matrix:
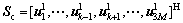 (5)
(5)
where 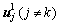 is the left singular vector of the interference channel from sector j to sector k on Subchannel c. When Subchannel c in sector j is not occupied, or the power reached sector k could be neglected,
is the left singular vector of the interference channel from sector j to sector k on Subchannel c. When Subchannel c in sector j is not occupied, or the power reached sector k could be neglected, 
The algorithm introduced in Eq.(4) does not need exchange the information of co-channel subscriber between sectors. It is a distributed schedule algorithm.
3.1 Distributed schedule algorithm based on orthogonal complement space
Orthogonal complement space theorem can be introduced to optimize the problem of inter-cell interference mitigation in Eq.(4). By row spanning the interference left singular vector matrix in Eq.(5), a row space is spanned:
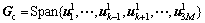 (6)
(6)
All the left singular vectors of co-channel interference subscribers at Subchannel c are in Gc, and Gc can be defined as the interferences space at Subchannel c in sector k. The orthogonal complement space of Gc is denoted as  and the subscribers in
and the subscribers in 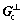 meet the restriction condition of Eq.(4) [3]. Therefore, the problem of optimization in Eq.(4) can be solved by schedule algorithm based on orthogonal complement space: in Uk, the subscriber is scheduled to have the maximum eigenvalue and its left singular vector is in the orthogonal complement space of its interference space.
meet the restriction condition of Eq.(4) [3]. Therefore, the problem of optimization in Eq.(4) can be solved by schedule algorithm based on orthogonal complement space: in Uk, the subscriber is scheduled to have the maximum eigenvalue and its left singular vector is in the orthogonal complement space of its interference space.
Base on the subspace theorem [3], the orthogonal complement space 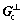 is the null space of Sc,
is the null space of Sc, 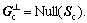 According to the spanning set theorem [3], the null space Null(Sc) is spanned by its base vectors. Let the rank of interference matrix Sc be γ. The null space Null(Sc) has (Nr-γ) base vectors. Normalized orthogonal base vectors could be constructed by SVD.
According to the spanning set theorem [3], the null space Null(Sc) is spanned by its base vectors. Let the rank of interference matrix Sc be γ. The null space Null(Sc) has (Nr-γ) base vectors. Normalized orthogonal base vectors could be constructed by SVD.
Let Sc=UΛV,  V=
V= 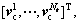 according to the properties of singular vectors:
according to the properties of singular vectors: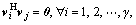 j=γ+1, γ+2, …, Nr. vγ+1, vγ+2, …,
j=γ+1, γ+2, …, Nr. vγ+1, vγ+2, …, 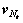 are the residual right singular vectors corresponding to zero singular values whose dimensions are Nr-γ. vγ+1, vγ+2, …,
are the residual right singular vectors corresponding to zero singular values whose dimensions are Nr-γ. vγ+1, vγ+2, …, 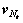 are linear uncorrelated vectors, which form the base vectors of null space Null(Sk):
are linear uncorrelated vectors, which form the base vectors of null space Null(Sk):
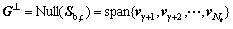 (7)
(7)
If the left singular vector of subscriber k currently scheduled is in Null(Sk), rank{ub,c,k, vγ+1, vγ+1, …, 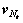 }=Nr-γ, then the optimization problem of Eq.(4) turns into
}=Nr-γ, then the optimization problem of Eq.(4) turns into
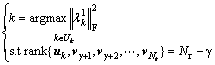 (8)
(8)
Eq.(8) is the distributed schedule (DS-OCS) algorithm based on orthogonal complement space.
3.2 Orthogonal complement schedule algorithm based on proportional fairness
The DS-OCS algorithm in Eq.(8) has the abilities of canceling inter-cell interference, and increasing system capacity; however, it runs short of fairness, that is, some subscribers have more chances to acquire subchannels; whereas other subscribers have less or no chance due to their poor eigenvalue or null space. Therefore, in order to keep fairness among all subscribers, by combining DS-OCS with proportional fairness schedule algorithm, the priority of proportional fairness and orthogonal complement space based schedule algorithm is calculated as
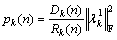 (9)
(9)
where Dk(n) is the attainable rate of the scheduled subscriber in sector k at Subchannel c, Rk(n) is the averaged rate of the scheduled subscriber until time n. If the subscriber is scheduled at time n, then
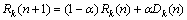 (10)
(10)
If the subscriber is not scheduled at time n, there is
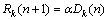 (11)
(11)
where 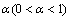 is the forgetting factor.
is the forgetting factor.
Substituting the eigenvalue with Eq.(9), the problem of inter-cell interference mitigation could be expressed as
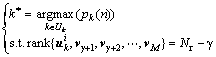 (12)
(12)
Eq.(12) is the distributing proportional fairness schedule algorithm based on the orthogonal complement space (DPFS-OCS).
4 Simulation results and analyses
The simulated scenario is the downlink in the 3GPP LTE system, and system level simulations are performed. The system bandwidth is 10 MHz. Seven cells are divided into 21 sectors. The distance between neighboring BS is 1 732 m. In order to cancel the edge influence, the capacity of center cells is examined only. Channel model is in accordance with Table 4.1 in 3GPP TR25. 996, where CASE I, NLOS scenario is selected. The carrier frequency is 2 GHz. The environment parameters comply with the urban micro-cell parameters listed in Table 5.1 of 3GPP TR25.996. The modeling of inter-cell interference is based on the proposal of Section 5.7 in 3GPP TR25.996. The BS equips four transmit antennas, and the maximum transmit power is 46 dB?m. The wireless channel is assumed to be static within one transmission time interval (TTI). There are 50 subscribers in each sector, and each subscriber equips two receiving antenna and moves with a velocity of 3 km/h.
Using the Mont-Carlo method, the system throughput of DS-OCS and DPFS-OCS algorithm is simulated. The methodology of Mont-Carlo is described as follows:
1) Read simulation parameters at the beginning of each snapshot;
2) Generate 50 subscribes and locate their situations;
3) Calculate the interference from the BSs to the subscribes;
4) Schedule the suitable subscribe and select modulation and coding scheme (MCS) according to the BLER curve;
5) Calculate the throughput according to MCS;
6) Average the throughput among snapshots.
Fig.1 shows the average system throughput of different schedule algorithms. The cell throughput increases with the transmit power increasing, but with a decreased rate. The DPFS-OCS algorithm improves the system throughput by 6%-10% compared with PF algorithm according to Fig.1. The DPFS-OCS algorithm adopts transmitting and receiving beamforming to reduce the inter-cell interference, and optimizes the subchannel schedule based on the maximum eigenvalues; therefore, higher signal to interference plus noise ratio (SINR) is obtained, which is related to the higher MCS index. The system throughput increases with the MCS index.
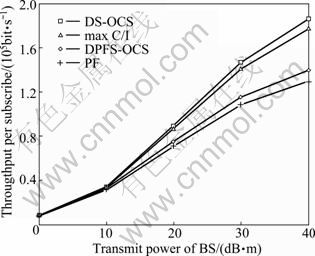
Fig.1 Average system throughput with different schedule algorithms
The DS-OCS algorithm aims at maximizing the system throughput like the max C/I algorithm. Furthermore, the DS-OCS algorithm mitigates the interference as the DPFS-OCS algorithm does. Fig.1 shows that DS-OCS algorithm gets 2%-4% system throughput increase over the max C/I algorithm.
It is clear that the system throughput gap becomes larger as the transmitting power increases in Fig.1. The difference comes from the interference increase with the transmitting power increasing.
The subscribers that locate at 80%-100% of cell radius from the center of the cell are defined as the edge subscribers. Fig.2 presents the average throughput of 5% edge subscribers with different schedule algorithms. The subscribers around the center have much higher SINR, so the DS-OCS and max C/I algorithm apply the most of the frequency source to the subscribers around the center. The DPFS-OCS and BF algorithm distribute the frequency source according to the fairness. The throughput of 5% edge subscribers adopting DPFS-OCS and BF algorithm is much higher than that adopting DS-OCS and max C/I algorithm.
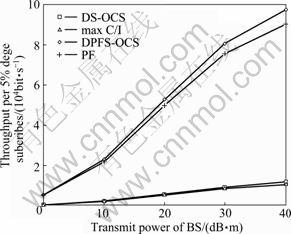
Fig.2 Average throughput of 5% edge subscribers with different schedule algorithms
5 Conclusions
1) SVD of the channel is performed and the first right singular vector is selected as the beamforming vector to improve the signal to noise ratio at the subscriber and reduce the interference to other subscribers.
2) The interference space is spanned according to the spanning set theorem. The orthogonal complement space of the interferences space is set up.
3) Based on the orthogonal complement space, the DS-OCS algorithm is proposed, which has the abilities of canceling the inter-cell interference. The system capacity is increased by 2%-4%.
4) In order to keep fairness among all subscribers, by combining DS-OCS with proportional fairness schedule algorithm, the DPFS-OCS algorithm is proposed. The DPFS-OCS algorithm has a system capacity improvement of 6%-10% for the edge- subscribers.
References
[1] 3GPP. Physical layer aspects for evolved UTRA: US TR 25. 814 [P]. 2006-09-22.
[2] 3GPP TSG-RAN WG1#42, Ericsson. Inter-cell interference handling for E-UTRA: UK R1-050764 [P]. 2005-08-26.
[3] XIONG Xiong, GE Jian-hua, LI Jing, TANG Yun-shuai. Cooperative diversity based on rotation code [J]. Journal of Central South University of Technology, 2009, 16(2): 0280-0284.
[4] ZHANG Xian-da. Matrix analysis and applications [M]. Beijing: TsingHua University Press, 2004: 592-595. (in Chinese)
[5] SANG G K, KYONGKUK C, DONGWEON Y, YOUNG J K, JAE K K. Performance analysis of downlink inter cell interference coordination in the LTE-Advanced system [C]// Fourth International Conference on Digital Telecommunications. Colmar, France: IEEE Press, 2009: 30-33.
[6] QIANG Yong-quan, VIVIER G, YANG Jin, XU Ning. Inter-cell interference modeling for OFDMA systems with beamforming [C]// IEEE 68th Vehicular Technology Conference. VTC 2008-Fall. Calgary, Canada: IEEE Press, 2008: 1-5.
[7] MAO Xue-hong, MAAREF A, KOON H T. Adaptive soft frequency reuse for inter-cell interference coordination in SC-FDMA based 3GPP LTE uplinks [C]// GLOBECOM 2008. New Orleans: IEEE Press, 2008: 1-6.
[8] RAHMAN M, YANIKOMEROGLU H, WONG W. Interference avoidance with dynamic inter-cell coordination for downlink LTE system [C]// Wireless Communications and Networking Conference. Budapest Hungary: IEEE Press, 2009: 1-6.
[9] YOSIA H, LARS T. Distributed base station cooperation via block-diagonalization and dual-decomposition [C]// IEEE GLOBECOM 2008. New Orleans: IEEE Press, 2008: 1-5.
[10] LI Zhong-nian, WANG Ya-feng. A hybrid inter-cell interference mitigation scheme for OFDMA system [C]//ICCS 2008. Guangzhou: IEEE Press, 2008: 657-660.
[11] R1-060291, 3GPP TSG-RAN WGA Meeting #44, Nokia OFDMA downlink inter-cell interference mitigation [R]. Denver, Colorado, 2006.
[12] ZHANG Xun-yong, CHEN He, JIANG Ling-ge. Inter-cell interference coordination based on softer frequency reuse in OFDMA cellular systems [C]// ICCNNSP 2008. Zhenjiang: IEEE Press, 2008: 270-275.
[13] LIU Yi, ZHANG Hai-lin. Precoding for the multiuser MIMO- OFDMA downlink with limited feedback [J]. Journal of Xidian University, 2007, 34(1): 71-75. (in Chinese)
[14] REN T M, RICHARD J. Downlink beamforming algorithms with inter-cell interference in cellular networks [J]. IEEE Transactions on Wireless Communication, 2006, 5(10): 2814-2823.
[15] GUO Yi, LIU Gang, GE Jian-hua. Iterative channel estimation with noise reduction for MIMO-OFDM systems [J]. Journal of Xidian University, 2008, 35(2): 196-200. (in Chinese)
(Edited by YANG Bing)
Foundation item: Projects(2009ZX03003-003, 2009ZX03003-004) supported by the Major National Science & Technology Program; Project(B08038) supported by the “111” Project; Project(HX0109012417) supported by Huawei Technologies Co., Ltd, China; Project(IRT0852) supported by Program for Changjiang Scholars and Innovative Research Team in Chinese University
Received date: 2009-09-16; Accepted date: 2010-10-14
Corresponding author: GE Jian-hua, Professor, PhD; Tel: +86-29-88202516; E-mail: jhge@xidian.edu.cn