Size and shape effects on Curie temperature of ferromagnetic

nanoparticles

CAO Ling-fei(曹玲飞)¹, XIE Dan(谢 丹)², GUO Ming-xing(郭明星)³, H.S. Park¹, T. Fujita¹

1. School of Engineering, University of Tokyo, Bunkyo-ku, Tokyo 113-8656, Japan;

2. Laboratory of Crystallography, Department of Materials, ETH-Zürich, CH-8093 Zürich, Switzerland;

3. School of Materials Science and Engineering, Central South University, Changsha 410083, China

Received 15 July 2007; accepted 10 September 2007

Abstract: A simplified model was developed to describe the Curie temperature suppression of ferromagnetic nanoparticles. Based on a size and shape dependent model of cohesive energy, the critical temperature variations of ferromagnetic nanoparticles were deduced. It is predicted that the Curie temperature of nanoparticles depends on both size and shape conditions, among which the temperature suppression is strongly influenced by the particle size and the shape effect is comparably minor. The calculation values for freestanding nanoparticles are in good agreement with other theoretical model and the experimental results. The model is also potential for predictions for the nanoparticles embedded in different substrates.

Key words: nanoparticle; size effect; shape effect; ferromagnet; Curie temperature

1 Introduction

In recent years, ferromagnetic nanoparticles have been extensively investigated due to their scientific and industrial importance, and unique properties resulting from their ultrafine sizes. It has been reported that when the size reduces to a nanometer, ferromagnetic solids may exhibit superparamagetism[1], higher coercive force[2], giant magnetoresistance[3], phase transforma- tion[4] and lower Curie temperature[5-9]. The last point of Curie temperature T_C suppression, namely, T_C of ferromagnetic nanoparticles decreases with decreasing diameter, is quite interesting for the development of new functional materials, such as switches functioning in a designed temperature range with tunable T_C, temperature sensitive ferromagnets applied in magnetic fluids[10].

Some models have been developed to understand the experimental observations of T_C suppression.The first one should be mentioned is the scaling theory established by FISHER and BARBER[6] for finite-size effects in  ferromagnetic systems. Based on the spin-spin correlation length (SSLC, ξ) mechanism, it is predicted that if the nanosolid size is smaller than the critical SSCL, the T_C will shift to a lower temperature T_C(D) than the bulk value T_C(∞), and the relationship can be expressed by a step function as

 (D＞ξ)                  (1)

 (D＜ξ)                      (2)

where  D is the size of nanocrystals, r denotes the thickness of a monolayer, and λ is the corresponding critical exponent. Though the original model is limited in a thin film system, the pioneering conception strongly impacts general understandings on the Curie temperature suppression. For example, NIKOLAEV and SHIPILIN [11] have proposed a T_C(D) function for ferromagnetic nanoparticles as

                           (3)

where ΔL is the thickness of surface layer of nanoparticles, characterizing the influence of the surface layer on the Curie temperature in light of exchange bond variations. However, when this model is utilized to fit experimental data for Fe₃O₄ nanoparticles of different sizes, a constant ΔL is unsuccessful in the full size range of nanometer. This may be caused by the variation of ΔL with the solid size, and the relationship between ΔL and D is expected to be established.

Another approach has been reported by SUN et al [7]. In their work, the bond order-length-strength(BOLS) correlation mechanism is incorporated into the Ising premise to advance a unified expression for T_C  predictions of ferromagnetic, ferroelectric and superconductive nanosolids. The lower Curie temperature is related to the decrease of atomic cohesive energy that caused by the coordination number(CN) imperfection of the lower coordinated atoms near the surface edge. In other terms, JIANG et al[8,12] have discussed the size and interface effects on the critical temperatures mentioned above. Based on a size-dependent cohesive energy model, a unified function is modeled to predict the T_C suppression with decreasing nanocrystal size. The same prediction is also obtained in their discussion on the Curie transition temperature of ferromagnetic low-dimensional metals (particles, wires and thin films) with different morphologies in full size range.

All these developed models are significant to understand the nature of T_C suppression of ferromagnetic nanosolids from different perspectives. However, another important aspect of particles, the shape of nanoparticles has not been paid enough attention to in some work. Currently, the shape of nanoparticles is generally regarded as spherical type in thermal calculation, while depending on different production conditions, particles may also exhibit cubic, columnar, polyhedral and other shapes. For a nanoparticle with the same size, different shapes lead to different specific surfaces, which can remarkably influence its physicochemical properties [13-16]. Therefore, variations on the shape of nanoparticles should not be ignored. For a better understanding of both size and shape effects on the Curie temperature variation of ferromagnetic nanoparticles, a simplified model was developed in this work. Based on the cohesive energy model and the relationship between Curie temperature and cohesive energy, the temperature variations for freestanding ferromagnetic nanoparticles were described. The Curie temperature of nanoparticles embedded in substrate films was discussed as well.

2 Model

The Curie temperature is a critical parameter for ferromagnetic nanoparticles, which is determined by the spin-spin exchange interaction. Upon a temperature higher than the Curie point of ferromagnets, the exchange interaction caused by the spin magnetic moment of neighboring 3d electrons will be very weak or even disappear. At that time, the spin-spin interaction is disordered by thermal stimulus, and ferromagnet becomes paramagnet of magnetic disorder. To destroy the magnetic exchange, sufficient energy has to be provided to break all atomic bonds and promote the atoms for thermal vibration. During this process, the total energy, or exchange interaction energy E_exc(T) can be regarded to equal the sum of the cohesive energy E and the thermal vibration energy E_v(T) needed to disorder the spin-spin interaction, namely,

E_exc(T)=E+E_v(T)                             (4)

Based on a mean field approximation, the thermal vibration energy has a proportional relationship with temperature, i.e., E_v(T)=k_BT, where k_B is the Boltzmann constant. At Curie temperature, the thermal vibration energy required to disorder the exchange interaction is a portion of the atomic cohesive energy at T=0[7-8, 17-18]. From this point of view, the Curie temperature can be regarded directly proportional to the cohesive energy (T_C∝E) as a first order approximation, since the nature of any phase transition is related with the potentials of the two related phases. As an empirical result,

                                  (5)

where  E and T_C denote cohesive energy and Curie temperature, and the subscripts n, b denote nanoparticle, corresponding bulk respectively. According to Eqn.(5), the Curie temperature T_C should have the same size and shape dependence as cohesive energy E. In this term, to figure out the size and shape effects on cohesive energy becomes critical to develop a size and shape dependent model for the Curie temperature of ferromagnetic nanoparticles. This concept is helpful to understand the Curie temperature variations of ferromagnetic nanoparticles, especially for the comparison within the same series of sample system.

3 Results and discussion

3.1Calculation of cohesive energy

The cohesive energy equals the energy needed to destroy all bonds when dividing the crystal into isolated atoms, namely, the cohesive energy is directly determined by the product of the bond amount and its unit energy[15-16, 19-20]. Supposing the bond energy equals each other for the same atom, the cohesive energy will depend on its bond amount. For nanoparticles, due to the well-known surface effects, the values of cohesive energy are not all the same for the superficial part and interior part, caused by their thermal behavior difference. One case in point is their atomic relaxation caused by surface coordination-number imperfection[21]. Such a difference for finite particles cannot be ignored, so the cohesive energy of nanoparticles should be the sum of the superficial part and the interior part. Accordingly, we obtain the surface-to-volume atomic ratio dependent expression for cohesive energy of nanoparticles as follows:

E_n=(1-α)E_b+αE_s                              (6)

where  the subscript ‘s’ represents the surface, α means the surface-to-volume atomic ratio. Supposing the bond amount of interior atom is m, the bond amount of a surface atom with interior atoms is (1/4) m for simplicity. Such opinion is supported by Ref.[22], where the surface relaxation is regarded as only about one-fourth of the area of each surface atom embedded in the lattice. Then we obtain Eqn.(7) for freestanding nanoparticles and Eqn.(8) for embedded nanoparticles[15-16]:

                               (7)

                       (8)

where  the subscript M denotes the embedding matrix, η represents the misfit between nanoparticles and matrix. In a case of incoherent interface between nanoparticles and matrix, η=0; and for a completely coherent interface, η=1. One point that should be noted is that behaviors between freestanding nanoparticles and embedded ones with incoherent interface are not quite the same. So if set η=0 in Eqn.(8), E_n/E_b=1-(3/8)α will be obtained for an incoherent interface between particles and matrix, which is not consistent with Eqn.(7) for freestanding nanoparticles. A possible reason for such phenomenon may be that the thermal vibration amplitudes of surface atoms are less than those of interface atoms, which leads to the above different behaviors between freestanding and embedded nanoparticles.

In Eqns.(7) and (8), α denotes surface-to-volume atomic ratio, where the surface details should be noted. Usually, the nanoparticle is simplified as spherical shape for calculation. Then according to the definition, the surface-to-volume atomic ratio can be described as

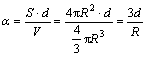                    (6)

where  d is the atom diameter, R is the nanoparticle radius, and the surface is assumed to be shell structure consisting of one layer of atoms. Similarly, supposing the shape of the nanoparticle is ideal cubic,α can be deduced as

                           (10)

where  n denotes the atomic number of nanocrystals, C is the atomic number of one structure cell, and k is the ratio between equivalent atomic radius and lattice parameter. For FCC, BCC and HCP structures, C are 4, 2 and 2, and k are ,  and 1/2, respectively [24].

Substituting Eqn.(10) into Eqn.(7), the cohesive energy for freestanding nanoparticles can be described as [23]

                    (11)

As shape variation is significant to the thermal properties of nanoparticles, a shape factor μ can be defined as the ratio of two surface areas to describe the difference between non-cubic and cubic particles, i.e.,

                                 (12)

where  S is the surface area of the particle in random shape, and S_cubic is the surface area of the cubic particle, which is supposed to have the same volume as the former. The conception of shape factor is especially practical benefit when the experimental observation of particle shape is combined with theoretical prediction. For example, the particle shape may be determined by the high resolution transmission electron microscopy (HRTEM), then the shape factor can be figured out and used in an exact prediction, such as thermal stability of nanomaterials[16].

Combining Eqns.(11) with (12), the cohesive energy of freestanding nanoparticles with random shape can be described as

                       (13)

Based on the same conception, the cohesive energy of nanoparticles under embedded condition is

              (14)

3. 2 Calculation of Curie temperature

Based on the size-and-shape dependent model of cohesive energy, the Curie temperature of ferromagnetic nanoparticles can be further deduced. Considering that the Curie temperature is proportional to the cohesive energy, it is reliable to express the Curie temperature of nanoparticles with both size and shape dependence as

For freestanding nanoparticles:

                       (15)

For embedded nanoparticles:

             (16)

From the above expressions of Curie temperature in Eqns.(15) and (16), it is obvious that when the atoms that constitute a nanoparticle are determined, the parameters C and k are fixed. Then the Curie temperature of the nanoparticle is strongly dependent on its shape factor and atomic number. Here the atomic number can be regarded as one index of particle size, as it is natural that more atoms lead to larger size of nanoparticles. The values of shape factor for nanoparticles in different shape can be calculated according to their geometric characters and the definition in Eqn.(12). Calculation results for some typical shapes are listed in Table 1. Accordingly, it’s safe to say that the Curie temperature of a nanoparticle depends on its size and shape effects, as well as its cohesive energy.

Table 1 Values of shape factor μ for nanoparticles

Meanwhile, comparison between Eqns.(15) and (16) suggests that the size and shape effects for freestanding nanoparticles will be more remarkable than those for embedded ones, as the latter depends on more variables in Eqn.(16). This phenomenon can be partly explained in the way that the freestanding materials have a larger surface-to-volume atomic ratio, so that their size and shape dependence is stronger than the embedded particles. For a certain nanoparticle, for example, freestanding Fe nanoparticles in cubic shape, the parameters μ, C, k and T_Cb in Eqn.(13) are 1, 2,and 1 043 K, respectively. Then the relationship between the Curie temperature of nanoparticles and their atomic number can be plotted. Under different conditions, the parameters may change and the corresponding values of Curie temperature can be obtained.

3.3 Model validity and discussion

To validate the reliability of our model, the Curie temperatures of ultrafine Fe, Co and Ni particles are numerically shown in Fig.1 with the reported experimental values. From Fig.1, it is clear that the Curie temperatures of ferromagnetic nanoparticles decrease with the decreasing size (described by the amount variation of atoms), which is in good accordance with the experimental observations mentioned before. The curves in Fig.1 are also compatible with the prediction by other theoretical models[7-8,12]. It is also interesting to find that the Curie temperature difference caused by shape effect becomes obvious only within a quite ultrafine size range, i.e. below 10 nm. Therefore, in a general situation, more emphases should be put on the size effect. Furthermore, compared the calculation curves with the available experimental data for Ni nanoparticles, it seems that the experiment data are well located in or between our prediction lines representing nanoparticles in cubic shape and spherical shape. Considering that the measured particles are approximating sphere together with other shapes, our prediction is in good accordance with the experimental data.

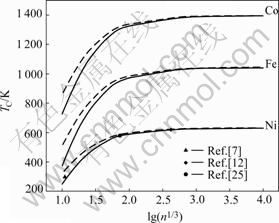
Fig.1 T_C function for freestanding Fe, C, Ni nanoparticles in terms of Eqn.(15) shown as solid lines for spherical shape and dash lines for cubic shape

For the systems of embedded nanoparticles, Curie temperature also depends on the interaction between the particle and substrate, together with the parameters mentioned above. When there is no or a weak interaction at the interface, the embedded nanoparticles may behave similarly to freestanding nanoparticles, namely the Curie temperature will decrease with the decreasing size. In case of a strong interaction or higher value of Curie temperature of the matrix (T_CM  in Eqn.(16)), the Curie temperature of the embedded nanoparticle maybe change in an opposite way. Such phenomenon can also be explained in a view of energy variation. It has been reported that there exist different degrees of spin-spin interactions between inner and surface atoms, caused by the number reduction of spin interactions on the surface. This will lead to a variation of lattice vibration. Therefore, when the size is decreased, the total energy, or the thermal vibration energy to disorder the ferromagnetic ordering state may change with the interaction conditions[26]. Until now, magnetic particles embedded in Ag or Cu matrix are two major types of particle-film giant magnetoresistance(GMR) materials in industry and research work. However, their Curie temperature variations for the embedded nanoparticles are not easily available at present. Eqn.(16) with parameters properly chosen will be helpful to be referred in theoretical investigation and practical production.

Furthermore, based on the definition of surface-to-volume atomic ratio α, there should be a direct relationship among the values of α for nanoparticles, nanowires and nanofilms with the same size R. For nanoparticles, R means the normal radius; for nanowires, R denotes the radius of the cross section; and for nanofilms, R represents the half value of the thickness. Accordingly, it can be deduced that for different low-dimensional systems, the surface-to-volume mole ratio is in the ratio of α_sphere?α_film?α_wire=3?2?1, where α_sphere, α_film and α_wire are the surface-to-volume atomic ratio for nanoparticles, nanowires and nanofilms, respectively [16]. Then the above cohesive energy formulae and Curie temperature for particles can be extended to describe the properties of corresponding wires or films.

4 Conclusions

1) A simplified model is developed for the size-and- shape dependent Curie temperature of ferromagnetic nanoparticles, based on the relationship between the Curie temperature and cohesive energy.

2) The model predicts a decrease of Curie temperature with decreasing size of ferromagnetic nanoparticles. The shape of nanoparticles also plays an important role on the critical temperature variation within a quite ultrafine size range.

3) The simple model developed in this work agrees well with the available experimental data and other theoretical predictions.

References

[1] TANG N J, ZHONG W, JIANG H Y, WU X L, LIU W, DU Y W. Nanostructured magnetite (Fe₃O₄) thin films prepared by sol-gel method [J]. J Magn Magn Mater, 2004, 282: 92-95.

[2] QIU Z Q, DU Y W, TANG H, WALKER J C. SYNK J E, VENDULA K. A M?ssbauer study of fine iron particles [J]. J Appl Phys Rev, 1988, 63(8): 4100-4104.

[3] MILNER A, GERBER A, GROISMAN, KARPOVSKY M, GLADKIKH A. Spin-dependent electronic transport in granular ferromagnets [J]. Phys Rev Lett, 1996, 76: 475-478.

[4] MENG Q, ZHOU N, RONG Y, CHEN S, HSU T Y. Size effect on the Fe nanocrystalline phase transformation [J]. Acta Mater, 2002, 50(18): 4563-4570.

[5] ZHONG W H, SUN C Q, LI S, BAI H L, JIANG E Y. Impact of bond-order loss on surface and nanosolid magnetism [J]. Acta Mater, 2005, 53(11): 3207-3214.

[6] FISHER M E, BARBER M N. Scaling theory for finite-size effects in the critical region [J]. Phys Rev Lett, 1972, 28: 1516-1519.

[7] SUN C Q, ZHONG W H, LI S, TAY B K, BAI H L, JIANG E Y. Coordination imperfection suppressed phase stability of ferromagnetic, ferroelectric, and superconductive nanosolids [J]. J Phys Chem B, 2004, 108(3): 1080-1084.

[8] YANG C C, JIANG Q. Size and interface effects on critical temperatures of ferromagnetic, ferroelectric and superconductive nanocrystals [J]. Acta Mater,2005, 53(11): 3305-3311.

[9] EVANS R, NOWAK U, DORFBANER F, SHREFL T, MRYASOV O, CHANTRELL R W, GROCHOLA G. The influence of shape and structure on the Curie temperature of Fe and Co nanoparticles [J]. J Appl Phys, 2006, 99: 08G703-1-3.

[10] BERKOVSKI B, BASHTOVOV V. Magnetic fluids and applications handbook [M]. Wallingford: Begell House, 1996.

[11] NIKOLAEV V I, SHIPILIN A M. The influence of breaking of exchange bonds on the Curie temperature [J]. Phys Solid State, 2003, 45: 1079-1080.

[12] CUI X F, ZHAO M, JIANG Q. Curie transition temperature of ferromagnetic low-dimensional metals [J]. Thin Solid Films, 2005, 472(1/2): 328-333.

[13] XIE D, QI W H, WANG M P. Size and shape dependent melting-thermodynamic properties of metallic nanoparticles [J]. Acta Metall Sin, 2004, 40(10): 1041-1044. (in Chinese)

[14] WAUTELET M, DAUCHOT J P, HECQ M. On the phase diagram of non-spherical nanoparticles [J]. J Phys Condens Matt, 2003, 15: 3651-3655.

[15] XIE D, WANG M P, QI W H. A simplified model to calculate the surface-to-volume atomic ratio dependent cohesive energy of nanocrystals [J]. J Phys: Condense Mater, 2004, 16: L401-L405.

[16] CAO L F, XU G Y, XIE D, GUO M X, LUO L, LI Z, WANG M P. Thermal stability of Fe, Co, Ni metal nanoparticles [J]. Phys Status Solid (B), 2006, 243: 2745-2755.

[17] ZHANG Ren-jun, WILLIS R F. Thickness-dependent Curie temperatures of ultrathin magnetic films: Effect of the range of spin-spin interactions [J]. Phys Rev Lett, 2001, 86: 2665-2668.

[18] SUN C Q, WANG Y, TAY B K, LI S, HUANG H, ZHANG Y B. Correlation between the melting point of a nanosolid and the cohesive energy of a surface atom [J]. J Phys Chem B, 2002, 106(41): 10701-10705.

[19] SUN C Q, TAY B K, ZENG X T, LI S, CHEN T P, ZHOU J, BAI H L, JIANG E Y. Bond-order–bond-length–bond-strength (bond-OLS) correlation mechanism for the shape-and-size dependence of a nanosolid [J]. J Phys: Condense Mater, 2002, 14: 7781-7795.

[20] XIE Dan, QI Wei-hong, WANG Ming-pu. Equivalent model on melting and superheating of metallic nanocrystals [J]. Acta Metall Sin, 2004, 41(5): 458-462. (in Chinese)

[21] KIM H K, HUH S H, PARK J W, JEONG J W, LEE G H. The cluster size dependence of thermal stabilities of both molybdenum and tungsten nanoclusters [J]. Chemical Physics Letters, 2002, 354(1/2): 165-172.

[22] ADAMSON A W. Physical chemistry of surface [M]. New York: John-Wiley & Sons Inc, 1990.

[23] XIE Dan, WANG Ming-pu, CAO Ling-fei. A simplified model to calculate the higher surface energy of free-standing nanocrystals [J]. Phys Status Solid (B), 2005, 242(8): R76-R78.

[24] ASKELAND D R, PHULE P P. The science and engineering of materials [M]. New York: Thomson Learning Inc, 2003: 84.

[25] DU You-wei, XU Ming-xiang, WU Jian, SHI Ying-bing, LU Huai-xian, XUE Rong-hua. Magnetic properties of ultrafine nickel particles [J]. J Appl Phys, 1991, 70: 5903-5905.

[26] LANG X Y, ZHENG W T, JIANG Q. Size and interface effects on ferromagnetic and antiferromagnetic transition temperatures [J]. Phys Review B, 2006, 73: 224444-1-8.

(Edited by LI Xiang-qun)

Foundation item: Project(FY2006) supported by the JSPS Postdoctoral Fellowship For Foreign Researches; Project supported by the 21st Century COE Program, “Mechanical Systems Innovation,” by the Ministry of Education, Culture, Sports, Science and Technology, Japan

Corresponding author: CAO Ling-fei; Tel: +81-3-5841-7079; Fax: +81-3-5841-7075; E-mail: caolingfei@gmail.com