用热分解法从CdCO3前驱体制备CdO纳米颗粒的反应路径和反应动力学
来源期刊:中国有色金属学报(英文版)2016年第4期
论文作者:Gholam Reza KHAYATI Seyed Hadi SHAHCHERAGHI Vahid LOTFI Esmael DAREZARESHKI
文章页码:1138 - 1145
关键词:CdCO3;CdO纳米颗粒;动力学建模;热分解;改进等转换率法
Key words:CdCO3; CdO nanoparticle; kinetic modeling; thermal decomposition; advanced isoconversional method
摘 要:研究用热分解法从CdCO3前驱体制备CdO纳米颗粒的非等温动力学。采用Malek模型模拟法和改进的非模型等转化率Vyazovkin法对所得DSC和TDA数据进行分析。结果表明,从CdCO3制备CdO纳米颗粒的反应属于自动催化反应。Sestak-Berggren模型能很好地描述该反应过程。另外,计算得到CdCO3热分解反应的表观活化能为(119.19±9.97) kJ/mol,并建立了该热分解反应的反应速率方程。
Abstract: The non-isothermal kinetics of CdO nanoparticles prepared from CdCO3 precursor using thermal decomposition method was investigated. A model-fitting Malek approach and a model-free advanced isoconversional method of Vyazovkin were applied to the analysis of the DSC and TGA data. The results showed that CdO nanoparticles prepared from CdCO3 followed an autocatalytic reaction. Sestak–Berggren model could favorably describe the studied reaction process. Moreover, the apparent activation energy of CdCO3 decomposition was calculated to be (119.19±9.97) kJ/mol and the explicit rate equation form of CdCO3 decomposition was established.
Trans. Nonferrous Met. Soc. China 26(2016) 1138-1145
Gholam Reza KHAYATI1, Seyed Hadi SHAHCHERAGHI2,3, Vahid LOTFI1, Esmael DAREZARESHKI3
1. Department of Materials Science and Engineering, Shahid Bahonar University of Kerman, P. O. Box No. 76135-133, Kerman, Iran;
2. Department of Advanced Science and Technology, Shahid Bahonar University of Kerman, P. O. Box No. 76135-133, Kerman, Iran;
3. Mineral Industries Research Centre, Shahid Bahonar University of Kerman, P. O. Box No. 76135-133, Kerman, Iran
Received 23 April 2015; accepted 19 October 2015
Abstract: The non-isothermal kinetics of CdO nanoparticles prepared from CdCO3 precursor using thermal decomposition method was investigated. A model-fitting Malek approach and a model-free advanced isoconversional method of Vyazovkin were applied to the analysis of the DSC and TGA data. The results showed that CdO nanoparticles prepared from CdCO3followed an autocatalytic reaction. Sestak–Berggren model could favorably describe the studied reaction process. Moreover, the apparent activation energy of CdCO3 decomposition was calculated to be (119.19±9.97) kJ/mol and the explicit rate equation form of CdCO3 decomposition was established.
Key words: CdCO3; CdO nanoparticle; kinetic modeling; thermal decomposition; advanced isoconversional method
1 Introduction
Recently, nanoparticles have become the focus of modern materials science because of their potential technological importance and unique physical properties [1]. Metal oxide nanoparticles have some unique physical and chemical properties which make them superior to conventional metal oxide in many applications [2]. CdO is an important n-type semiconductor with a direct band gap of 2.5 eV and an indirect band gap of 1.98 eV. Consequently, it has promising applications in catalysts, sensors, nonlinear materials, solar cells, and other optoelectronic devices [3,4].
In our previous work, a facile technique for the CdO nanoparticles preparation from the anodic materials of the spent Ni-Cd batteries by thermal decomposition method was presented [5]. Practically, the proposed method has advantages such as easy to control and no need of costly reactants. But it suffers from conceptual principles. Some of the most important restrictions are ambiguity of the mechanism during the thermal decomposition and appropriate identification of reaction route. In solid state reactions, appropriate kinetic equations, rate limiting steps and calculation of kinetic parameters could supply a deeper conception into the possible mechanisms of transformation [6].
The mechanism and kinetics of carbonates of thermal decomposition to produce particles in micron or larger scale were studied previously according to the isothermal conditions [7-13]. Nevertheless, to the best of our knowledge, non-isothermal kinetics modeling of CdO nanoparticles preparation from carbonates (in particular, CdCO3 precursor) by thermal decomposition method has not been investigated yet.
It is necessary to note that strictly isothermal experiments are not possible, because there is always a finite non-isothermal heat-up time. The most disadvantages of isothermal trials are limited temperature ranges. At lower temperatures, it may be very difficult to obtain complete conversion over a reasonable time period. While at higher temperatures, the heat-up time becomes comparable to the characteristic time of process, which means that a significant extent of conversion is obtained before the isothermal regime sets in. The problem of non-zero conversion is easy to avoid in constant heating rate trials by starting heating from the temperature that is below the temperature at which a process becomes detectable [14].
In this work, the non-isothermal kinetics of process was investigated using DSC and TGA with a model- fitting Malek approach and a model-free advanced isoconversional method of Vyazovkin. Then, the results were compared with isothermal conditions [9-13]. Our current contribution will provide the comprehensive data to better understand the mechanism of CdCO3 decomposition.
2 Experimental
The raw material, i.e., CdCO3, was taken from the anodic material of spent Ni-Cd batteries [5]. To study the kinetics of CdCO3 decomposition, the precursor (7±0.5) mg was studied through DSC-TGA (STA409PG) at four heating rates of 5, 10, 15 and 20 °C/min in the temperature range of 25-600 °C in air. For each sample and heating rate, three repetitive TGA curves were obtained in order to assure the reproducibility of the results.
The crystalline structure, morphology and size of CdO nanoparticles were characterized by XRD (Philips, X' pert-MPD system using Cu Kα) and HRSEM (Hitachi S-4160), respectively. IR spectra were recorded in the wave length range of 400-4000 cm-1 with a resolution of 4 cm-1, using Bruker tensor 27 FTIR spectrometer with RT-DIATGS detector and KBr pellet technique. The histogram of nanoparticle size distribution was estimated from the HRSEM images by randomly measuring the diameters of at least 650 particles.
3 Theoretical
Generally, the rate of degradation reaction can be described in terms of two functions, i.e., k(T) and f(α), thus,
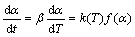 (1)
(1)
where α is the degree of conversion, t is the reaction time, T is the thermal dynamic temperature, β is the heating rate, k(T) is the rate constant, and f(α) is the type of reaction or function of reaction mechanism. In TGA analysis, the degree of conversion can be defined as the ratio of actual mass loss to the total mass loss corresponding to the decomposition process [15,16]:
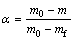 (2)
(2)
where m0, m and mf are the initial, actual and final masses of the sample, respectively. The dependence of the reaction rate constant on temperature can be described by Arrhenius equation:
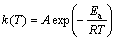 (3)
(3)
where A is the pre-exponential factor, R is the mole gas constant (8.314 J/(mol·K), and Ea is the apparent activation energy. A relatively complete thermal analysis kinetics method proposed by MALEK [17] was chosen to analyze the non-isothermal experiment data. The Malek method contains two functions, y(α) and z(α), to find the appropriate kinetic model that best describes the conversion function of the studied process. They are as follows [17,18]:
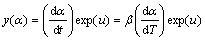 (4)
(4)
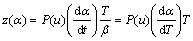 (5)
(5)
where u=Ea/(RT) and P(u) is the expression of the temperature integral, which can be well approximated by the fourth rational expression as shown in Eq. (6) [17,18-21]:
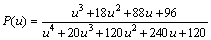 (6)
(6)
Function y(α) is proportional to function f(α), being characteristic for a given kinetic model. The shapes and maxima of both y(α) and z(α) functions, normalized within (0, 1) interval, provide valuable information for determining the most appropriate kinetic model to describe the process studied.
According to the Malek method, Ea must be determined independently using other methods. To estimate the activation energy, various methods have been proposed. These methods can be generally categorized as isoconversional and model-fitting methods [15,16,22-27].
In addition, there are more complex “model-free” methods, such as the nonlinear isoconversional method by VYAZOVKIN and WIGHT [28] and VYAZOVKIN [29], solutions of which can only be obtained using computer algorithms. Due to great calculation accuracy and versatile applicability for various heating programs [15,16,18,20], the advanced isoconversional method developed by VYAZOVKIN, that is, the VYAZOVKIN method, was adopted to analyze the non-isothermal reaction. Specifically, the Vyazovkin method is applicable to a non-isothermal kinetic process with a series of linear heating, which can be written as [14-16,18,20]:
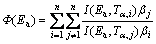 (7)
(7)
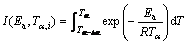 (8)
(8)
where βi and βj represent different heating rates, Tα and Tα–△α are the reaction temperatures corresponding to α and △α, respectively. Minimizing Eq. (7) for each α with a certain conversion increment (usually △α=0.05) results in the correction of Ea with α. The detailed descriptions of how to use the Vyazovkin method to treat calorimetric data can be acquired elsewhere [15,16].

Fig. 1 XRD patterns of precursor CdCO3 (a) and CdO nanoparticles prepared at heating rate of 10 °C/min (b)
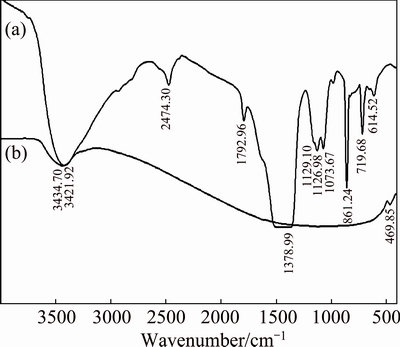
Fig. 2 FTIR spectra of precursor CdCO3 (a) and CdO nanoparticles (b)
4 Results and discussion
4.1 Synthesis of CdO nanoparticles
Figure 1(a) shows the XRD pattern of CdCO3 precursor. As shown, all diffraction peaks were consistent with CdCO3 (QCPDS card No. 00-042-1342). Figure 1(b) shows typical XRD pattern of CdO nanoparticles prepared at the heating rate of 10 °C/min. Accordingly, the precursor was completely decomposed at about 500 °C into single phase of the pure crystallite CdO (QCPDS card No. 00-005-0640). This result was confirmed by TGA-DSC observation. Figures 2(a) and (b) show the FT-IR spectra of precursor CdCO3 and CdO nanoparticles prepared at the heating rate of 10 °C/min, respectively. The peaks (Fig. 2(a)) of around 1380, 860, and 719 cm–1 are the characteristic vibration bands of CO32- [30,31]. The absorption bands at 614 and 1129 cm–1 are attributed to sulfate groups (SO42–) [2,30]. In Fig. 2(b), the peak at around 470 cm–1 is assigned to Cd—O of CdO, confirming the formation of pure CdO nanoparticles [30,31]. And, the peak at 3400 cm–1 corresponds to the OH— stretching [2,31].
Figure 3(a) shows HRSEM image of CdCO3 precursor and Fig. 3(b) shows the typical image of CdO nanoparticles prepared at the heating rate of 10 °C/min. Accordingly, single CdO particles exhibit a strong tendency to form nanoparticle agglomerates. The solid- state reconstruction of nanoparticles into aggregates is a usual phenomenon showing a tendency of nano- particulate systems to restrain unsaturated surface forces via surface recombination [32]. EDX analysis of CdO nanoparticles (Fig. 3(c)) confirms the high purity of the products. The size distribution histogram of the CdO nanoparticles (Fig. 3(d)) reveals that the size of CdO particles varies from 8 to 108 nm.
4.2 Non-isothermal decomposition of CaCO3 precursor
The TGA-DSC curves of non-isothermal degradation of the CaCO3 precursor for four different heating rates (5, 10, 15, and 20 °C/min) are shown in Fig. 4. Accordingly, mass loss of about 26% found between 311 and 462 °C (endothermic peak) was related to the decomposition of CdCO3 into CdO and CO2 [31]. Moreover, with increasing the heating rate, the TGA curve and peak of DSC curve shifted to a higher temperature, and the final mass loss presented a decreasing trend.
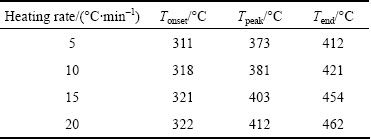
From Fig. 4, with increasing the heating rate, the reaction area was shifted to a higher temperature range. Moreover, onset reaction temperatures, peak temperatures, and end temperatures were enhanced with increasing heating rate (Table 1).
The conversional curves (α-T) for non-isothermal decomposition of CdCO3 are indicated in Fig. 5. These conversional curves exhibit the sigmoidal profile, and with increasing heating rate, the curves shift toward the higher temperature. In other words, the higher the heating rate, the higher the temperature for the reaction to reach the identical α.
4.3 Calculation of activation energy (Ea)
The dependence of Ea on α for the decomposition of CdCO3 is presented in Fig. 6. According to Refs. [33,34], if Ea values were independent of α, the decomposition process was dominated by a single reaction step. Moreover, if the difference between the maximum and minimum values of Ea (i.e., 19.93 kJ/mol) was less than 20%-30% of the average Ea (i.e., 119.86 kJ/mol), the activation energy was independent of α [15,16].
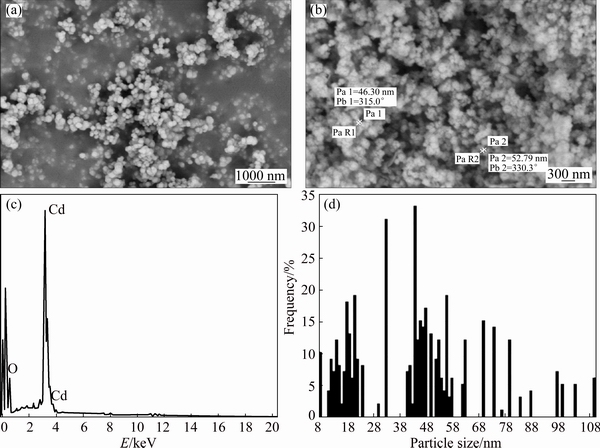
Fig. 3 HRSEM image of CdCO3 precursor (a) and typical image of CdO nanoparticles prepared at heating rate of 10 °C/min (b), EDS pattern of CdO nanoparticles (c) and histogram of CdO nanoparticle size distribution (d)
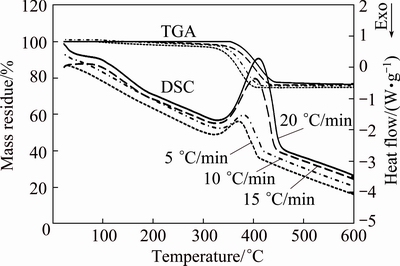
Fig. 4 TGA-DSC curves for thermal decomposition of precursor CdCO3 at heating rates of 5, 10, 15 and 20 °C/min in air
Table 1 Typical parameters of thermal decomposition of CdCO3precursor
Therefore, from Fig. 6, it is obvious that CdCO3 decomposition is a single-step process. Based on the Vyazovkin method, Ea showed an almost stable behavior with the average of Ea=(119.19±9.97) kJ/mol which falls within the expected range of literature, i.e., 96-135 kJ/mol [9-13].
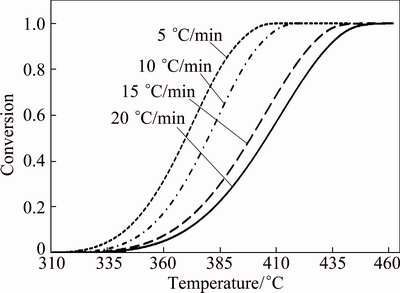
Fig. 5 Conversion-temperature curves for thermal decomposition of CdCO3 precursor at heating rates of 5, 10, 15 and 20 °C/min in air
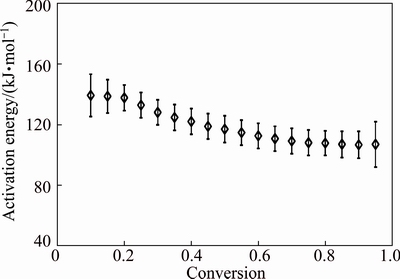
Fig. 6 Dependence of activation energy (Ea) on conversion (α) for thermal decomposition of CdCO3precursor
Furthermore, the variation of Ea for α<0.10 and α>0.90 was not of the major concern, because the parameters were affected hardly by the startup of the experiment and by minor errors in baseline determination, respectively [14]. It should be mentioned that, the dependence of Ea on α was a source of additional kinetic information of process [35-37]. The results indicated that the dependence of Ea on α helped not only to reveal the complexity of reduction processes, but also to identify its kinetic scheme. Therefore, at following, the suitable kinetics model for describing CdO nanoparticles processing from spent Ni–Cd batteries using thermal decomposition method was determined.
4.4 Determination of most probable reaction mechanism function
Figure 7 shows the relationship between the reaction rate and conversion of decomposition of CdCO3. Accordingly, the reaction rate (βdα/dT) increased with the increase of the heating rate. Furthermore, the peak reaction rate appeared in the conversion (αp) range of 0.598-0.609. Hence, the model-free kinetic method was suitable for the experiment.
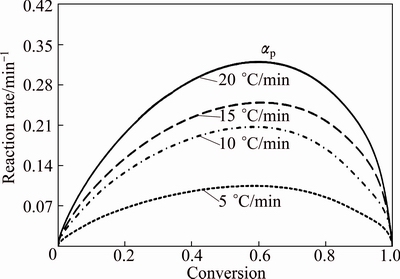
Fig. 7 Reaction rate (βdα/dT) as function of conversion (α) for thermal decomposition of CdCO3 precursor at heating rates of 5, 10, 15, and 20 °C/min in air
The normalized function curves of y(α) and z(α) were respectively constructed from Eqs. (4) and (5) for thermal decomposition of CdCO3 and shown in Fig. 8. As shown, the y(α) curves exhibited peak values in the conversion (αM) range of 0.228-0.237, and the z(α) curves showed a practically isoconversional peak value conversion, αp∞, within 0.653-0.659.
Table 2 shows the characteristic peak conversion values, i.e., αp, αM and αp∞, for the thermal decomposition of CdCO3. These findings demonstrated that the effect of the heating rates on the whole reaction kinetics could be omitted by applying the Malek method to the non-isothermal kinetics data of CdCO3 degradation. Furthermore, the peak value of y(α) appeared while α was much larger than 0, implying that the reaction is auto-catalyzed [38]. Besides, the larger value of αM indicated increasing the autocatalytic tendency of the decomposition process [39].
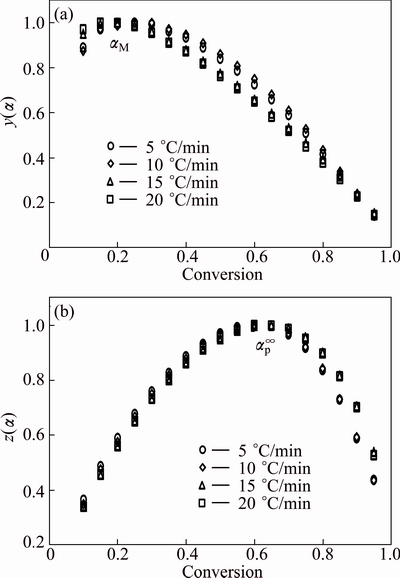
Fig. 8 Plots of normalized y(α) (a) and z(α) (b) against conversion (α) for thermal decomposition of CdCO3 precursor at heating rates of 5, 10, 15 and 20 °C/min in air
Table 2 Characteristic peak conversion values, i.e., αp, αM and αp∞, for thermal decomposition of CdCO3precursor
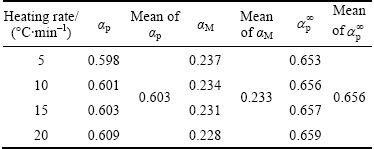
According to the shape of y(α) and characteristic values of y(α) and z(α), it can be concluded that the truncated Sestak-Berggren model or the two-parameter Sestak-Berggren model [17,38,39] or extended Prout–Tompkins model (the regular Prout–Tompkins model, i.e., f(α)=α(1-α)), SB (m, n), was suitable for kinetic modeling of CdCO3 degradation. Moreover, from Table 2, it can be observed that 0<αM<αp∞ and αp∞≠0.632, which strongly indicated that the truncated SB (m, n) [39] was suitable. SESTAK and BERGGREN [39] proposed an empirical model for f(α):
f(α)=αm(1-α)n[-ln(1-α)]s (9)
According to the Sestak-Berggren model, the combination of m, n, and s can be represented a number of different reaction models. It was generally applied in truncated form (s=0 in Eq. (9)). The truncated Sestak–Berggren model was an example of an autocatalytic model. According to the truncated SB (m, n) model and Eq. (3), Eq. (1) can be transformed into the following form [39]:
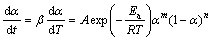 (10)
(10)
where m and n are the reaction orders, and other parameters have the same meaning as the above equations. The ratio of m to n, i.e., p, equals αM/(1-αM) according to MALEK [17]. Thus, Eq. (10) can be transformed into the following form:
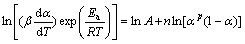 (11)
(11)
The kinetic parameter n can be derived from the slope of ln(βdα/dT)exp[Ea/(RT)] versus ln[αp(1-α)] for 0.2<α≤0.95 [38], the intercept is ln A, and m=pn. These data perform good linearity (Fig. 9). The values of m, n, and ln A could be calculated from the intercept and slope of these fit straight lines, which are listed in Table 3. These kinetic parameters vary slightly with heating rates, with deviation less than 10% of their average values. In addition, the higher value of the kinetic parameter n (n>1) indicated the increasing complexity and the decreasing autocatalytic tendency of the degradation process [39].
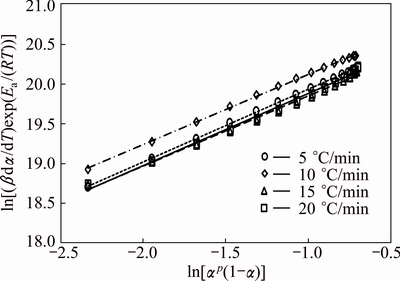
Fig. 9 Plots of ln[(βdα/dT)exp(Ea/(RT))] vs ln[αp(1-α)] for different heating rates for thermal decomposition of CdCO3 precursor for 0.2<α≤0.95 at heating rates of 5, 10, 15 and 20 °C/min in air
Table 3 Calculated kinetic parameters m, n and ln A for SB (m, n) model for thermal decomposition of precursor CdCO3
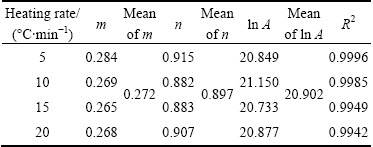
Therefore, the thermal decomposition of CdCO3 was a process with high autocatalytic tendency.
The sensitivity of SB model to the process features, such as the effect of heating rate, has been evidenced by the variation of the kinetic exponents. This clearly shows the flexibility of the SB empirical function in describing several shapes of the dα/dt against α curve satisfying the condition αM≠0. However, some limitations of the model due to its purely empirical character are to be accounted. Unfortunately, it is extremely difficult or even impossible to give a physical meaning to the kinetic exponent’s m and n of the SB model [39]. Thus, no theoretical models based on physico-geometric assumptions of the reaction interface movements were found to describe our experimental data, probably as a consequence of the complexity of the process under study. Nevertheless, these limitations are not critical considering the comparative nature of the kinetic study performed here.
Furthermore, the kinetic exponent’s m and n are parameters that define relative contribution of acceleratory and deceleratory part of the crystallization process. These parameters are rather empirical constant, and too much physical significance should not be attached to their numerical values [40].
By substituting the calculated kinetic parameters (n, m and ln A in Table 3 along with previously calculated Ea) into Eq. (10), the explicit rate equation for the decomposition reaction of CdCO3 was obtained as Eq. (12):
 ,
,
α∈[0.10,0.95] (12)
To check the predictability of the explicit kinetics model (Eq. (12)), the predicted rate curves for different heating rates were calculated (Fig. 10). As shown in Fig. 10, there was a good agreement between the experimentally obtained βdα/dT-T curves and numerically calculated rate curves, using the corresponding kinetic triplets, hence, the truncated SB (m, n) model was suitable for predicting decomposition rate of CdCO3.
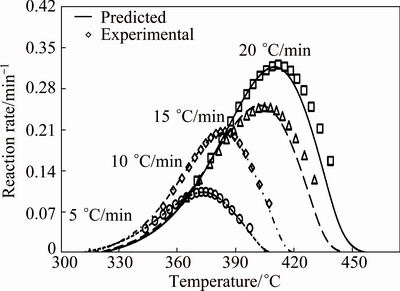
Fig. 10 Comparison of experimental reaction rate and that predicated from SB (m, n) model (Eq. (12)) vs temperature for thermal decomposition of CdCO3 precursor at heating rates of 5, 10, 15 and 20 °C/min in air
5 Conclusions
1) The non-isothermal kinetics of process was studied using DSC and TGA with a model-fitting Malek approach and a model–free advanced isoconversional method of Vyazovkin.
2) The decomposition of CdCO3 precursor was a single step process.
3) In the conversion (α) range of 0.10-0.95, Ea presented an almost stable behavior with the average value of Ea=(119.19±9.97) kJ/mol.
4) The thermal decomposition of CdCO3 precursor was a process with the high autocatalytic tendency.
5) There was a good agreement between the experimentally obtained βdα/dT-T curves and numerically calculated rate curves, using the corresponding kinetic triplets; hence, the truncated SB (m, n) model was suitable for predicting decomposition rate of CdCO3 precursor.
References
[1] DAREZERESHKI E, RANJBAR M, BAKHTIARI F. One-step synthesis of maghemite (γ-Fe2O3) nano-particles by wet chemical method [J]. Journal of Alloys Compounds, 2010, 502: 257-260.
[2] DAREZERESHKI E, BAKHTIARI F. A novel technique to synthesis of tenorite (CuO) nanoparticles from low concentration CuSO4 solution [J]. Journal of Mining and Metallurgy Section B: Metallurgy, 2011, 47: 73-78.
[3] REDDY S, SWAMY B E K, CHANDRA U, SHERIGARA B S JAYADEVAPPA H. Synthesis of CdO nanoparticles and their modified carbon paste electrode for determination of dopamine and ascorbic acid by using cyclic voltammetry technique [J]. International Journal of Electrochemical Science, 2010, 5: 10-17.
[4] BALU A R, NAGARETHINAM V S, SUGANYA M, ARUNKUMAR N, SELVAN G. Effect of the solution concentration on the structural, optical and electrical properties of solar deposited CdO thin films [J]. Journal of Electron Devices, 2012, 12: 739-749.
[5] KHAYATI G R, DALVAND H, DAREZERESHKI E, IRANNEJAD A. A facile method to synthesis of CdO nanoparticles from spent Ni-Cd batteries [J]. Materials Letters, 2014, 115: 272-274.
[6] TOMASHEVITCH K V, KALININ S V, VERTEGEL A A, OLEINIKOV N N, KETSKO V A, TRETYAKOV Y D. Application of non-linear heating regime for the determination of activation energy and kinetic parameters of solid-state reactions [J]. Thermochimica Acta, 1998, 323: 101-107.
[7] MULOKOZI A M, LUGWISHA E. New aspects of the decomposition kinetics of calcite. Part 1: Isothermal decomposition [J]. Thermochimica Acta, 1992, 194: 375-383.
[8] MULOKOZI A M. Kinetic parameters in heterogeneous kinetics [J]. Thermochimica Acta, 1992, 197: 363-372.
[9] MULOKOZI A M. The thermal decomposition kinetics of CdCO3 powder [J]. Thermochimica Acta, 1992, 202: 17-23.
[10] MURTHY M S, HARISH B R, RAJANANDAM K S, PAVAN KUMAR K Y A. Investigation on the kinetics of thermal decomposition of calcium carbonate [J]. Chemical Engineering Science, 1994, 49: 2198-2204.
[11] BULTOSA G, MULOKOZI A M. Kinetics of the thermal decomposition of cadmium carbonate (CdCO3) [J]. Journal of Thermal Analysis, 1995, 45: 1339-1343.
[12] LVOV B V. Mechanism and kinetics of thermal decomposition of carbonates [J]. Thermochimica Acta, 2002, 386: 1-16.
[13] GALWEY A K, BROWN M E. Thermal decomposition of ionic solids: Chemical properties and reactivities of ionic crystalline phases [M]. Amsterdam: Elsevier, 1999: 75-100.
[14] VYAZOVKIN S, BURNHAM A K, CRIADO J M, PEREZ-MAQUEDA L A, POPESCU C, SBIRRAZZUOLI N. ICTAC Kinetics Committee recommendations for performing kinetic computations on thermal analysis data [J]. Thermochimica Acta, 2011, 520: 1-19.
[15] SHAHCHERAGHI S H, KHAYATI G R, RANJBAR M. An advanced reaction model determination methodology in solid-state kinetics based on Arrhenius parameters variation—Part I: Thermal dehydration kinetic analysis of Cu4SO4(OH)6 [J]. Thermal Analysis and Calorimetry, 2015, 122: 175-188.
[16] SHAHCHERAGHI S H, KHAYATI G R, RANJBAR M. An advanced reaction model determination methodology in solid-state kinetics based on Arrhenius parameters variation—Part III: Thermal desulfurization kinetic analysis of CuO·CuSO4 [J]. Thermal Analysis and Calorimetry, 2016, 123: 221-229.
[17] MALEK J. The kinetic analysis of non-isothermal data [J]. Thermochimica Acta, 1992, 200: 257-269.
[18] SHAHCHERAGHI S H, KHAYATI G R. Arrhenius parameters determination in non-isothermal conditions for mechanically activated Ag2O-graphite mixture [J]. Transactions of Nonferrous Metals Society of China, 2014, 24(12): 3994-4003.
[19] SHAHCHERAGHI S H, KHAYATI G R. Kinetics analysis of the non-isothermal decomposition of Ag2O-graphite mixture [J]. Transactions of Nonferrous Metals Society of China, 2014, 24(9): 2991-3000.
[20] SHAHCHERAGHI S H, KHAYATI G R. The effect of mechanical activation on non-isothermal decomposition kinetics of Ag2O- graphite mixture [J]. The Arabian Journal for Science and Engineering, 2014, 39: 7503-7512.
[21] SENUM G I, YANG R T. Rational approximations of the integral of the Arrhenius function [J]. Thermal Analysis and Calorimetry, 1997, 11: 445-447.
[22] KHAYATI G R, JANGHORBAN K, SHARIAT M H. Isothermal kinetic study of mechanochemically and thermally synthesized Ag from Ag2O [J]. Transactions of Nonferrous Metals Society of China, 2012, 22(4): 935-942.
[23] EBRAHIMI-KAHRIZANGI R, ABBASI M H. Evaluation of reliability of Coats-Redfern method for kinetic analysis of non-isothermal TGA [J]. Transactions of Nonferrous Metals Society of China, 2008, 18(1): 217-221.
[24] ZHANG Xiang-hui, HE Chuan, WANG Ling, LIU Jing, DENG Miao, FENG Qian. Non-isothermal kinetic analysis of thermal dehydration of La2(CO3)3·3.4H2O in air [J]. Transactions of Nonferrous Metals Society of China, 2014, 24(10): 3378-3385.
[25] ZHANG Guang, YU Jun-xia, XU Zhi-gao, ZHOU Fang, CHI Ru-an. Kinetics of thermal decomposition of lanthanum oxalate hydrate [J]. Transactions of Nonferrous Metals Society of China, 2012, 22(4): 925-934.
[26] WU Yu-feng, DU Wen-bo, ZUO Tie-yong. Synthesis kinetics of Mg2Sn in Mg-Sn powder mixture using non-isothermal differential scanning calorimetry [J]. Transactions of Nonferrous Metals Society of China, 2009, 19(5): 1196-1200.
[27] GHOSH K S, GAO N. Determination of kinetic parameters from calorimetric study of solid state reactions in 7150 Al-Zn-Mg alloy [J]. Transactions of Nonferrous Metals Society of China, 2011, 21(6): 1199-1209.
[28] VYAZOVKIN S, WIGHT C A. Model-free and model-fitting approaches to kinetic analysis of isothermal and non-isothermal data [J]. Thermochimica Acta, 1999, 340-341: 53-68.
[29] VYAZOVKIN S. Thermal analysis [J]. Analytical Chemistry, 2006, 78: 3875-3886.
[30] ASHOKA S, CHITHAIAH P, CHANDRAPPA G T. Studies on the synthesis of cadmium carbonate nanowires and porous cadmium oxide powder [J]. Materials Letters, 2010, 64: 173-176.
[31] BAZARGAN A M, FATEMINIA S M A, ESMAEILPOUR M, BAHREVAR M A. Electrospinning preparation and characterization of cadmium oxide nanofibers [J]. Journal of Chemical Engineering, 2009, 155: 523-527.
[32] KHAYATI G R, JANGHORBAN K. An investigation on the application of process control agents in the preparation and consolidation behavior of nanocrystalline silver by mechanochemical method [J]. Advanced Powder Technology, 2012, 23: 808-813.
[33] GASKELL D R. Introduction to metallurgical thermodynamics [M]. 4th ed. New York: Taylor & Francis Books, Inc, 2003.
[34] JANKOVIC B, MENTUS S, JELIC D. A kinetic study of non-isothermal decomposition process of anhydrous nickel nitrate under air atmosphere [J]. Physica B, 2009, 404: 2263-2269.
[35] VYAZOVKIN S, WIGHT C A. Kinetics in solids [J]. Annual Review of Physical Chemistry, 1997, 48: 125-149.
[36] SBIRRAZZUOLI N, GIRAULT Y, ELEGANT L. Simulations for evaluation of kinetic methods in differential scanning calorimetry. Part 3—Peak maximum evolution methods and isoconversional methods [J]. Thermochimica Acta, 1997, 293: 25-37.
[37] VYAZOVKIN S. Evaluation of activation energy of thermally stimulated solid state reactions under arbitrary variation of temperature [J]. Journal of Computational Chemistry, 1997, 18: 393-402.
[38] MALEK J. A computer program for kinetic analysis of non-isothermal thermo-analytical data [J]. Thermochimica Acta, 1989, 138: 337-346.
[39] SESTAK J, BERGGREN G. Study of the kinetics of the mechanism of solid-state reactions at increasing temperatures [J]. Thermochimica Acta, 1971, 3: 1-12.
[40] RAHIM M A A, LATIEF A Y A, EL-KORASHY A, SABET M A. Kinetic analysis of crystallization process in amorphous Se90-xTe10Pbx glasses [J]. Materials Transactions, 2010, 51: 428-433.
Gholam Reza KHAYATI1, Seyed Hadi SHAHCHERAGHI2,3, Vahid LOTFI1, Esmael DAREZARESHKI3
1. Department of Materials Science and Engineering, Shahid Bahonar University of Kerman, P. O. Box No. 76135-133, Kerman, Iran;
2. Department of Advanced Science and Technology, Shahid Bahonar University of Kerman, P. O. Box No. 76135-133, Kerman, Iran;
3. Mineral Industries Research Centre, Shahid Bahonar University of Kerman, P. O. Box No. 76135-133, Kerman, Iran
摘 要:研究用热分解法从CdCO3前驱体制备CdO纳米颗粒的非等温动力学。采用Malek模型模拟法和改进的非模型等转化率Vyazovkin法对所得DSC和TDA数据进行分析。结果表明,从CdCO3制备CdO纳米颗粒的反应属于自动催化反应。Sestak-Berggren模型能很好地描述该反应过程。另外,计算得到CdCO3热分解反应的表观活化能为(119.19±9.97) kJ/mol,并建立了该热分解反应的反应速率方程。
关键词:CdCO3;CdO纳米颗粒;动力学建模;热分解;改进等转换率法
(Edited by Wei-ping CHEN)
Corresponding author: Gholam Reza KHAYATI; Tel: +98-915-1903477; Fax: +98-341-2114053; E-mail: khayatireza@gmail.com; khayati@uk.ac.ir
DOI: 10.1016/S1003-6326(16)64212-7

