高坝施工全过程导流风险多维评估
罗立哲1, 2,胡志根1,刘全1,易丽丽3
(1. 武汉大学 水资源与水电工程科学国家重点实验室,湖北 武汉,430072;
2. 长江勘测规划设计研究有限公司,湖北 武汉,430010;
3. 湖北省水利厅,湖北 武汉,430071)
摘要:高坝施工期导流系统风险受多种随机因素影响,为进行更全面、准确的风险评估,综合分析各随机影响因素,基于Monte-Carlo方法构建多维联合风险空间,利用联合概率分布的层次拟合方法分析风险空间数据特征,建立综合考虑水文、水力、工程费用与施工进度的多维联合风险评估模型,实现对高坝施工期全过程的导流方案风险分析及风险配置评估。结果表明施工导流系统多维联合风险研究方法能够合理反映导流度汛风险、施工进度风险、费用风险及三者之间的交互影响,准确评估高坝导流工程的风险状态和导流方案的风险配置优良度。
关键词:导流风险;多维评估;层次拟合方法;高坝施工全过程
中图分类号:TV511.3 文献标志码:A 文章编号:1672-7207(2014)03-0840-07
Multi-dimensional estimation for risk of diversion system in high-dam construction process
LUO Lizhe1, 2, HU Zhigen1, LIU Quan1, YI Lili3
(1. The State Key Laboratory of Water Resources and Hydropower Engineering Science,
Wuhan University, Wuhan 430072, China;
2. Changjiang Institute of Survey, Planning, Design and Research, Wuhan 430010, China;
3. Department of Water Resources of Hubei Province, Wuhan 430071, China)
Abstract: The risk of diversion system during high-dam construction process is always influenced by some random factors. In order to estimate the risk more completely and accurately, the random factors were simulated by Monte-Carlo method to structure a multi-dimensional risk analysis space, and the characterization of data in the space was analyzed by hierarchical fitting method, which helped to build a risk evaluation model for diversion system that considered hydrology, hydraulics, cost and schedule comprehensively. The case study proves that, with the multi-dimensional risk analysis method, the flood handling risk, schedule risk, cost risk and their mutual influence can be reflected rationally, and comprehensive risk and risk-collocation of diversion schemes in the whole high-dam construction process can be evaluated accurately.
Key words: risk of diversion; multi-dimensional estimation; hierarchical fitting method; high-dam construction process
高坝工程导流是一个多主体、多阶段的过程,一方面,各时段导流标准对应的来流情况确定了导流建筑物和主体建筑物的施工进度;另一方面, 导流建筑物和主体建筑物的施工进度又影响着导流各时段导流建筑物的规划及导流标准的确定,因此工程度汛安全、建设工期和工程费用是高坝施工管理的重点,也是影响导流风险分析的主要因素,三者之间相互联系,必须加以综合研究[1-2]。一般导流系统风险研究是对度汛风险、建设工期和工程费用进行单独估计,胡志根等[3]利用Monte-Carlo方法模拟施工洪水过程和泄流过程,通过统计分析模型确定围堰运行的动态风险; Nasir等[4]对施工进度安排表进行分析研究,提出了施工进度风险计算模型;钟登华等[5]将系统仿真、网络计划和系统评价等技术方法引入到大型工程的施工组织设计领域,对大型工程施工进度分析理论及其应用进行了研究;Warszawski等[6]针对传统的风险计算方法较为复杂,提出了实用的工程项目多因素风险计算方法;范锡峨等[7]利用Monte-Carlo方法建立了考虑水文水力不确定性和施工进度不确定性的施工导流系统综合风险分析模型,对坝体施工进度确定条件下的施工导流系统风险进行了分析。但以上研究均不能同时得到联合高置信的安全可靠度、费用和进度的估计值,所优选的导流方案在实际执行时,费用和进度超过估计值的风险很大,且单点估计也不能为决策者提供充足的主观选择空间[8-9]。导流系统是在一定的水文及水力条件、费用预算和进度计划的共同约束下运行,因此,导流系统风险是水文随机性、水力随机性、施工进度不确定性及施工费用不确定性的联合分布函数。本文作者基于Monte-Carlo方法和网络计划方法,建立施工导流系统的多维联合风险分析空间;基于空间数据和高坝施工的确定性逻辑关系,根据概率联合分布层次拟合分析理论,评估了高坝施工全过程的导流系统多维联合风险,提高了风险评估广度。
1 关键风险因素分析
1.1 度汛风险
施工期导流系统的度汛风险定义为:在施工导流过程中发生超过挡水建筑物挡水高程的洪水的频率;各施工阶段上游水位超过挡水建筑物挡水高程的可能性为:
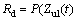 ≥
≥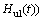 (1)
(1)
式中:Zul(t)为第t个施工阶段挡水建筑物上游水位;Hul(t)为第t个施工阶段挡水建筑物顶部高程。
该风险计算中主要有2个随机变量影响目标风险度:洪水随机过程和泄流能力随机过程。假设河流洪水序列(洪量)和泄流能力分布,利用Monte-Carlo方法模拟施工洪水过程和导流建筑物泄流过程,通过系统仿真进行施工洪水调洪演算, 用统计分析模型确定挡水建筑物上游水位分布可得到施工导流系统运行的安全风险。
1.2 进度风险
工程进度风险指施工项目的实际完工日期超过计划进度规定完成日期的概率,可表示为:
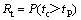 (2)
(2)
式中:tc为项目进度计划实际完工时间;tP为项目进度计划规定完成时间。
水利水电工程施工进度计划中的不确定性主要包括完成某工序所需实际施工时间估计的不确定性和每月有效施工时间的不确定性[10]。传统进度计划风险分析方法是根据工序之间的逻辑关系绘制网络图,按照各工序时间的概率分布,利用Monte-Carlo方法和CPM方法模拟项目进度计划实际完成情况[11-12],通过统计分析,得到施工进度计划风险。
1.3 费用风险
工程费用风险是指在规定施工阶段内工程项目实际投入费用超出其费用预算值的概率,可表示为:
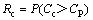 (3)
(3)
式中:Cc为工程项目实际实施消耗费用;CP为工程项目费用预算值。
水利水电工程费用中的不确定性主要包括实体投资的不确定性和动态费用的不确定性[13]。传统费用风险分析方法是根据各施工阶段工程费用的概率分布,利用Monte-Carlo方法模拟实际工程费用消耗,通过统计分析,得到工程费用风险[14]。
2 多维联合风险分析
高坝施工期导流系统风险是在一定上游水位、费用目标和进度计划联合约束下不能完成工程任务的概率,表示为:
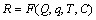 (4)
(4)
式中:Q为来流洪水过程的不确定性;q为泄洪能力的不确定性;T为施工工期的不确定性;C为工程费用的不确定性。但直接拟合函数F(Q, q, T, C)较复杂且计算量较大,因此本文在建立多维联合风险空间基础上,通过联合概率分布的层次拟合方法,建立施工期导流系统多维联合风险分析模型。
2.1 多维联合风险空间
对上游水位H、工程费用C和施工进度T进行联合仿真模拟,输出仿真结果进行联合频数统计和累计频数统计,建立多维联合风险空间。假设进行N次模拟仿真后输出结果(Hi, Ci, Ti), i=1, 2, …, n;取Hmin=min(H1, H2, …, Hn)和Hmax=max(H1, H2,…, Hn),对数域[Hmin, Hmax]进行统计区域划分为:[H*1, H*2), …, [H*k-1, H*k), …, [H*l-1, H*l],其中H*1=Hmin,H*l=Hmax;同理,取数域[Cmin, Cmax]和[Tmin, Tmax],并将其区域划分为:[C*1, C*2), …, [C*i-1,C*i), …, [C*m-1, C*m];[T*1, T*2), …, [T*j-1, T*j), …, [T*n-1, T*n]。建立三维联合风险空间 ,如图1所示。akij为仿真输出结果区域
,如图1所示。akij为仿真输出结果区域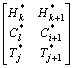 的频数。项目在
的频数。项目在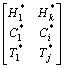 范围内完成的联合概率为:
范围内完成的联合概率为:
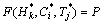 (H≤
(H≤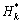 , C≤
, C≤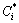 , T≤
, T≤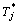 )=
)=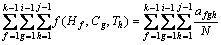 (5)
(5)
则综合考虑上游水位、费用与进度的联合风险率为:
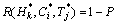 (H≤
(H≤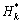 , C≤
, C≤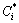 , T≤
, T≤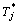 )=
)=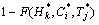 (6)
(6)
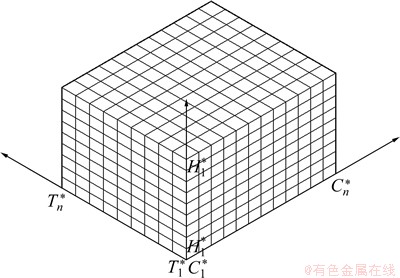

图1 多维风险分析空间示意图
Fig. 1 Schematic drawing of multi-dimensional risk analysis space
2.2 边缘风险与条件风险概率分析
在多维分布中仅考虑单个因素的概率分布称为该因素的边缘概率分布,多维风险空间中边缘分布可分为纯粹边缘分布和条件边缘分布。纯粹边缘分布指三个因素均为变量时,仅考虑一个因素的概率分布,如仅考虑上游水位H的边缘频数概率分布函数及边缘风险概率分布函数如式(7)~(8)所示;条件边缘分布指一个因素的取值或范围确定的情况下,仅考虑剩余因素中一个因素的概率分布,如当上游水位 时,费用C的条件边缘频数概率分布函数及条件边缘风险概率分布函数如式(9)和(10)所示。
时,费用C的条件边缘频数概率分布函数及条件边缘风险概率分布函数如式(9)和(10)所示。
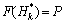 (H≤
(H≤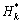 )=
)=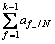 (7)
(7)
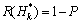 (H≤
(H≤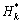 )=
)=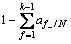 (8)
(8)
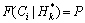 (C≤
(C≤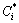 |H≤
|H≤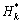 )=
)= (9)
(9)
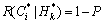 (C≤
(C≤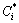 |H≤
|H≤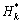 )=
)=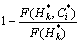 (10)
(10)
当多维风险空间中1个或2个因素变量取定值或取值范围一定时,估算其他分量的风险率分布称为条件风险概率分布。假设分量堰前水位H取值一定,费用C和进度T的联合条件频数概率分布函数及联合条件风险概率分布函数如式(11)~(12)所示;在此基础上,另一个分量,如费用C,取值或取值范围一定时,分量工期T的条件频数概率分布函数和条件风险概率分布函数如式(13)~(14)所示。当分量堰前水位H或进度T一定时,相关分布可依此类推。
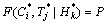 (C≤
(C≤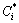 , T≤
, T≤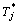 | H≤
| H≤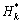 )=
)=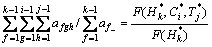 (11)
(11)
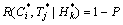 (C≤
(C≤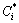 , T≤
, T≤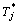 | H≤
| H≤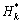 )=
)=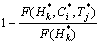 (12)
(12)
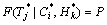 ( T≤
( T≤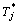 | C≤
| C≤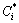 , H≤
, H≤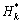 )=
)=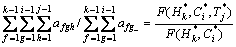 (13)
(13)
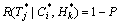 (T≤
(T≤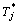 | C≤
| C≤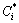 , H≤
, H≤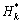 )=
)=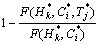 (14)
(14)
2.3 联合风险多维估计模型
通过仿真数据建立多维联合风险空间后,根据式(7)~(14)对空间数据进行层次拟合分析,得到各因素的边缘频数概率分布和条件频数概率分布;最后,建立综合考虑上游水位、费用和工期的联合风险多维估计模型,如式(15)~(16)所示,计算流程如图2所示。
 (15)
(15)
 (16)
(16)
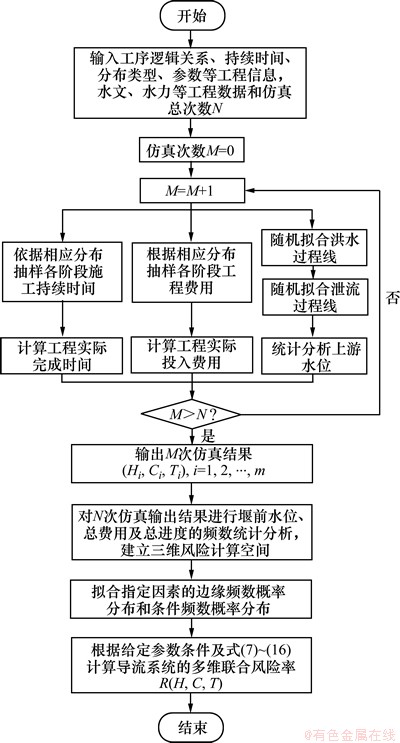
图2 施工导流系统联合风险计算流程
Fig. 2 Calculation flowchart of construction diversion system multi-dimensional risk
3 案例分析与讨论
3.1 工程概况
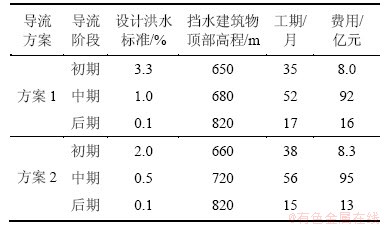
某电站装机12 600 MW,正常蓄水位810.00 m,坝顶高程820.00 m,双曲拱坝最大坝高280.00 m,正常蓄水位以下库容115.70亿m3。初步拟定导流建筑物为Ⅲ级,对应土石类围堰设计洪水标准的重现期为20~50 a;导流工程分为初期、中期和后期,其中初期导流以围堰作为挡水建筑物,中期和后期导流以坝体作为挡水建筑物。现拟定两个导流标准方案,且对2种方案各施工阶段的工程费用和施工进度进行了预算和计划拟定,如表2所示。
表1 设计洪水资料
Table 1 Flood data of design

表2 导流方案参数
Table 2 Parameters of diversion schemes
设定来流洪水序列(洪量)服从P-Ⅲ分布,影响泄流能力不确定性的泄流建筑物糙率值服从对称三角形分布,取值范围为0.013~0.016,进而泄流能力服从三角分布[2]。
导流及主体工程施工关键控制点之间的时间跨度及各阶段所需费用均假设服从三角概率分布TRLA(a,m,b)的随机变量[15](其中a为最乐观值,m为最可能值,b为最悲观值);表4所示为方案1工期和费用计算参数;表5所示为方案2工期和费用计算参数。
表3 工程施工控制性节点
Table 3 Control nodes of construction

表4 方案1工期和费用计划参数
Table 4 Planning parameters of construction period and cost in diversion scheme one
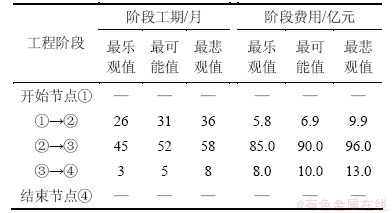
表5 方案2工期和费用计划参数
Table 5 Planning parameters of construction period and cost in diversion scheme two

3.2 联合多维风险率计算
对方案1初期导流阶段进行风险率分析,根据多维联合风险分析模型,进行N=3 000次独立重复仿真运行,可获得3 000组仿真输出数据(Hx, Tx, Cx),x=1, 2, …, 3 000,划分区间进行统计后,建立三维联合风险空间,拟合上游水位H的边缘频数概率分布曲线如图3所示,可得到F(H=650)=90.15%。
令上游水位H=650 m,通过统计可得费用和工期的联合条件频数分布F(Cg,Th|650),方案1初期导流费用和工期条件联合频数概率分布估计如表6所示,方案1初期导流工期和费用条件联合频数概率分布如图4所示。在二维联合条件频数分布中拟合费用C的条件边缘频数概率分布曲线,经拟合优度检验[16],高度服从均值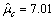 且
且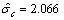 的正态分布,方案1初期导流费用条件边缘频数概率分布如图5所示,可得F(C=8.0| H=650)=0.919。
的正态分布,方案1初期导流费用条件边缘频数概率分布如图5所示,可得F(C=8.0| H=650)=0.919。

图3 方案1初期导流上游水位边缘频数概率分布
Fig. 3 Marginal probability distribution of water level upstream frequency during preliminary diversion period in diversion scheme one
当H=650且C=8.0时,工期T的条件频数概率分布曲线,经拟合优度检验,高度服从均值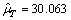 且
且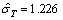 的正态分布,方案1初期导流工期条件频数概率分布如图6所示,可得F(T=35|C=6.9|H= 650)=0.991 8。
的正态分布,方案1初期导流工期条件频数概率分布如图6所示,可得F(T=35|C=6.9|H= 650)=0.991 8。
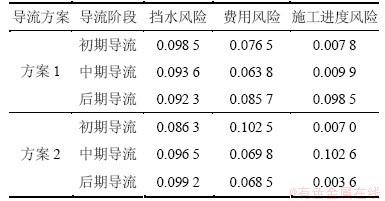
根据式(14)可得:方案1初期导流的联合频数概率为F(T=35, C=6.9, H=650)=F(T=35|C=8.0|H=650)× F(C=8.0|H=650)×F(H=650)=0.821,三维联合风险率R(T=35, C=8.0, H=650)=1-F(T=35, C=8.0, H=650)= 0.178 3。同理,根据表1~5数据、图2所示流程及式(6)~(15),可求得方案1其他导流阶段及方案2各导流阶段的多维联合风险率,施工导流系统多维联合风险如表7所示。同时,根据第1节中独立风险估计方法对2个方案各阶段进行了单因素风险评估,施工导流系统单因素风险如表8所示。
表6 方案1初期导流费用和工期条件联合频数概率分布估计
Table 6 Conditional probability distribution of cost and schedule joint frequency in diversion scheme one
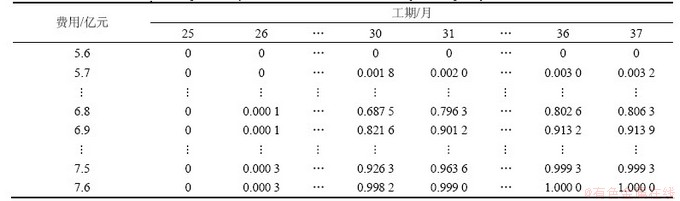
表7 施工导流系统多维联合风险
Table 7 Multi-dimensional risk of construction diversion system
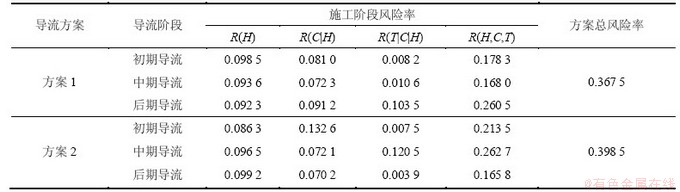
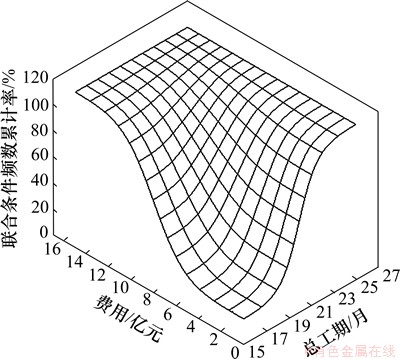
图4 方案1初期导流工期和费用条件联合频数概率分布
Fig. 4 Conditional probability distribution of cost and schedule joint frequency in diversion scheme one
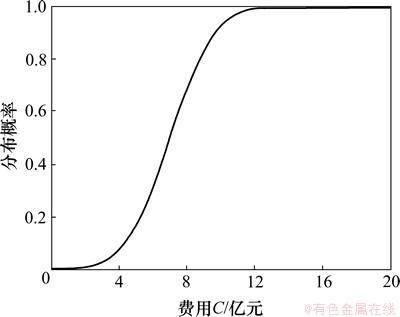
图5 方案1初期导流费用条件边缘频数概率分布
Fig. 5 Conditional marginal probability distribution of cost frequency during preliminary diversion period in diversion scheme one
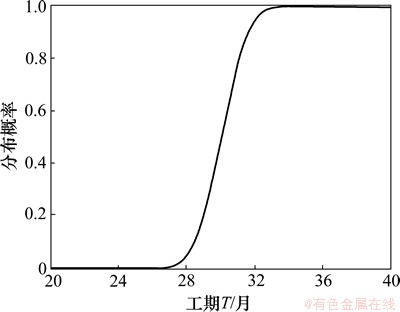
图6 方案1初期导流工期条件频数概率分布
Fig. 6 Conditional probability distribution of cost frequency during preliminary diversion period in diversion scheme one
表8 施工导流系统单因素风险
Table 8 Single-factor risk of construction diversion system
3.3 计算结果分析
根据表7对比总风险率可知方案1的风险配置优于方案2;同时,方案1后期导流阶段进度因素边缘风险率较高,建议将计划工期调整为19月或提高施工效率以保证工程按计划完成。由表7和表8对比可知:2个方案中各施工阶段的多维联合风险评估值均大于对应的单因素风险评估值,说明度汛、工程进度和工程费用对导流系统风险存在较高程度的交互式影响,利用多维联合风险模型评估实际工程导流系统风险能够充分反映各风险影响因素,更利于工程安全。
4 结论
(1) 在多维联合风险空间中,上游水位因素的边缘频数分布拟合结果为非常用分布,而工期因素和费用因素的边缘频数分布拟合结果高度符合正态分布。
(2) 根据多维风险评估模型分析得到的风险评估值大于传统单因素风险评估值,能够合理反映度汛、工程进度和工程费用之间的交互式影响,更准确地评估现实工程的风险状态和导流方案的风险配置优良度。
参考文献:
[1] 姚福海. 论水电工程施工洪水设计标准的合理选择[J]. 水力发电学报, 2007, 26(2): 65-69.
YAO Fuhai. Discussion on reasonable choice of hydropower projects construction design flood standard[J]. Journal of Hydroelectric Engineering, 2007, 26(2): 65-69.
[2] 王金国, 马光文, 蒋学林. 锦屏一级水电站围堰优化和调整研究[J]. 四川大学学报(工程科学版), 2010(2): 15-20.
WANG Jinguo, MA Guangwen, JIANG Xuelin. The optimization and adjustment of the cofferdam of Jinping Ⅰ Hydropower Station[J]. Journal of Sichuan University (Engineering Science Edition), 2010(2): 15-20.
[3] 胡志根, 刘全, 贺昌海, 等. 基于Monte-Carlo方法的土石围堰挡水导流风险分析[J]. 水科学进展, 2002, 13(5): 636-638.
HU Zhigen, LIU Quan, HE Changhai, et al. Risk analysis of retaining rockfill cofferdam for diversion based on the Monte-Carlo method[J]. Advances in Water Science, 2002, 13(5): 636-638.
[4] Nasir D, McCabe B, Hartono L. Evaluating risk in construction schedule model (ERIC-S): Construction schedule risk model[J]. Journal of Construction Engineering and Management, 2003, 129(5): 518-527.
[5] 钟登华, 李景茹, 刘奎建. 全过程动态仿真技术及其在大型工程施工管理中的应用[J]. 天津大学学报, 2003, 36(3): 347-352.
ZHONG Denghua, LI Jingru, LIU Kuijian. Dynamic simulation technique for whole construction processes and its application to large-scale construction project[J]. Journal of Tianjin University, 2003, 36(3): 347-352.
[6] Warszawski A, Sacks R. Practical multifactor approach to evaluating risk of investment in engineering projects[J]. Journal of Construction Engineering and Management, 2004, 130(3): 357-367.
[7] 范锡峨, 胡志根, 靳鹏. 基于Monte-Carlo方法的施工导流系统综合风险分析[J]. 水科学进展, 2007, 18(4): 604-608.
FAN Xi’e, HU Zhigen, JIN Peng. Integrated risk of construction diversion system based on the Monte-Carlo method[J]. Advances in Water Science, 2007, 18(4): 604-608.
[8] 王振强, 钟登华. 基于模拟技术的大型水电项目财务风险分析[J]. 土木工程学报, 2005, 38(5): 122-126.
WANG Zhenqiang, ZHONG Denghua. Simulation-based financial risk analysis for larger-scale hydropower projects[J]. China Civil Engineering Journal, 2005, 38(5): 122-126.
[9] 钟登华, 蔡绍宽, 李玉钦. 基于网络分析法(ANP)的水电工程风险分析及其应用[J]. 水力发电学报, 2008, 27(1): 11-17.
ZHONG Denghua, CAI Shaokuan, LI Yuqin. Risk analysis of hydropower project based on analytic network process and its application[J]. Journal of Hydroelectric Engineering, 2008, 27(1): 11-17.
[10] 刘俊艳, 王卓甫. 工程进度风险因素的非叠加性影响[J]. 系统工程理论与实践, 2011, 31(8): 1517-1523.
LIU Junyan, WANG Zhuofu. Non-additivity analysis on scheduling risks based on Bayesain networks[J]. Systems Engineering-Theory & Practice, 2011, 31(8): 1517-1523.
[11] 王卓甫, 欧阳红祥, 李红仙. 水利水电施工搭接网络进度风险计算[J]. 水利学报, 2003(1): 98-102.
WANG Zhuofu, OUYANG Hongxiang, Li Hongxian. Risk calculation of precedence network schedule for hydraulic projects[J]. Journal of Hydraulic Engineering, 2003(1): 98-102.
[12] 孙成双, 王要武. 基于多Agent技术的工程项目风险管理系统构架[J]. 哈尔滨工业大学学报, 2005, 37(6): 776-778.
SUN Chengshuang, WANG Yaowu. A multi-agent based system framework for construction project risk management[J]. Journal of Harbin Institute of Technology, 2005, 37(6): 776-778.
[13] 胡振华, 贺艳琼. 风险投资项目的分阶段风险评价研究[J]. 中南大学学报, 2007, 13(4): 442-445.
HU Zhenhua, HE Yanqiong. Study on the staged risk assessment of venture capital project[J]. Journal of Central South University, 2007, 13(4): 442-445.
[14] Onder O, Ahmet O. Construction cost analysis under uncertainty with correlated cost risk analysis model[J]. Construction Management and Economics, 2010, 8(2): 203-212
[15] 刘仁辉, 张劲强, 韩喜双. 三角模糊数的工程项目风险识别[J]. 哈尔滨工业大学学报, 2008, 40(10): 1617-1620.
LIU Renhui, ZHANG Jingqiang, HAN Xishuang. Risk identifiation based on triangular fuzzy number for construction project[J]. Journal of Harbin Institute of Technology, 2008, 40(10): 1617-1620.
[16]  Gamero M D, Alba Fernández V,
Gamero M D, Alba Fernández V,  J, et al. Goodness-of-fit tests based on empirical characteristic functions[J]. Computational Statistics and Data Analysis, 2009, 53(12): 3957-3971.
J, et al. Goodness-of-fit tests based on empirical characteristic functions[J]. Computational Statistics and Data Analysis, 2009, 53(12): 3957-3971.
(编辑 陈爱华)
收稿日期:2013-03-09;修回日期:2013-05-06
基金项目:国家自然科学基金资助项目(51279137,51079115)
通信作者:罗立哲(1987-),男,湖北省潜江市人,博士研究生,从事施工组织与管理和施工仿真方面研究;电话:18502779082;E-mail: wwtony@whu.edu.cn