
J. Cent. South Univ. (2019) 26: 1807-1819
DOI: https://doi.org/10.1007/s11771-019-4135-2
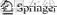
Stress-drop effect on brittleness evaluation of rock materials
SHI Gui-cai(史贵才)1, CHEN Guan(陈冠)2, PAN Yu-tao(潘玉涛)3,YANG Xiao-li(杨小礼)4, LIU Yong(刘勇)2, DAI Guo-zhong(代国忠)1
1. College of Civil Engineering & Architecture, Changzhou Institute of Technology,Changzhou 213002, China;
2. State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China;
3. Department of Civil and Environmental Engineering, National University of Singapore,12 Kent Ridge Road, 119221, Singapore;
4. School of Civil Engineering, Central South University, Changsha 410075, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Abstract: Uniaxial or triaxial compression test of cylindrical rock specimens using rock mechanics testing machine is a basic experimental method to study the strength and deformation characteristics of rock and the development process of rock fracture. Extensive literature review has been conducted on this issue; meanwhile, experimental and numerical studies have been conducted on the stress-drop effect on the brittleness of rock materials. A plastic flow factor of λ is proposed to describe the stress-drop effect. Evaluation methods of the factor λ corresponding to the four yield criteria of rock mass are proposed. Those four yield criteria are Tresca criterion, von-Mises criterion, Mohr-Coulomb criterion and Drucker-Prager criterion. For simplicity purposes, an engineering approximation approach has been proposed to evaluate the stress-drop with a non-zero strain increment. Numerical simulation results validated the effectiveness of the plastic flow factors λ as well as the engineering approximation approach. Based on the results in this study, finite element code can be programmed for brittle materials with stress-drop, which has the potential to be readily incorporated in finite element codes.
Key words: rock material; stress-drop effect; plastic flow factor; strength criteria
Cite this article as: SHI Gui-cai, CHEN Guan, PAN Yu-tao, YANG Xiao-li, LIU Yong, DAI Guo-zhong. Stress-drop effect on brittleness evaluation of rock materials [J]. Journal of Central South University, 2019, 26(7): 1807-1819. DOI: https://doi.org/10.1007/s11771-019-4135-2.
1 Introduction
Rock is a complex material. The uniaxial and triaxial compression tests of cylindrical rock specimens using rock mechanics testing machine are basic experimental approaches to study the strength and deformation characteristics of rock and the development process of rock fracture. The relationship between the axial force applied by the testing machine to the rock specimen and the axial deformation of the specimen during the rock uniaxial compression test is usually called the force-displacement curve. If the force and displacement are converted to nominal stress and strain, it can also be called the stress-strain curve. It is well known that no matter what type of testing machine is used, the peak strength of the rock can be obtained by a uniaxial compression test of the rock. The force-displacement curve before reaching the peak state is called the pre-peak characteristic curve. The force-displacement curve with a relatively steady residual behavior after the peak state is called the post-peak characteristic curve. The complete force-displacement curve, including the pre-peak and post-peak characteristic curves, is called the full-process curve, or the full-path curve. Studying the whole process curve of stress and strain, especially the characteristics of the post-peak region have always been a topic of great concern to the rock mechanics, because it is of great significance in the theory and practice of rock engineering. For example, the rock mass has been subjected to many severe tectonic movements after its formation, and it has been damaged to varying degrees. Therefore, the material properties of the in-situ rock mass are likely to be related to the post-peak area of the rock.
The earliest triaxial test was carried out on a common test machine. The round shaft rock sample was placed in a hydraulic chamber, and the rock sample was laterally loaded by oil pressure, and the confining pressure was maintained. Then, axial load was exerted on top of the sample. The triaxial compression curve of the Carrara marble published was investigated [1]. However, the peak post-zone characteristic curve of rock is difficult to find with ordinary rock mechanics testing machines. In order to obtain a complete whole process curve and study the peak post-zone characteristics of rocks, scholars in the field of rock mechanics have made various efforts since the 1960s. LABUZ et al [2] obtained the whole process curve of a series of rock samples and discussed the topics of strength and stability in relation to tensile and compressive testing of rock. The first time the triaxial compression process curve of Tenness marble was obtained on the rigid testing machine. It is pointed out that according to the stability of the uniaxial compression failure of the rock sample, the rock can be divided into type I and type II [3], and the type II curve represents the rock type with very obvious brittleness. WONG et al [4] reviewed recent advances in the brittle- ductile transition in porous rock and provided useful insights into the mechanics of brittle-ductile transition based on comparison of the model predictions with laboratory and microstructural observations. In addition, triaxial compression tests [5] with and without confining pressure were conducted on solid specimens and hollow cylinder specimens filled with aluminum, lead, and polymethyl methacrylate (PMMA) to investigate the strength, deformation and failure characteristics of circular roadways subjected to high axial stress. Despite the various experimental studies, the numerical simulation [6, 7] of the highly brittle material still remains scarce. In this study, a rational plastic flow factor λ is proposed to describe the stress-drop effect. A numerical example of a uniaxial test of a very brittle material using such approach is conducted.
2 Description of sudden reduction of stress
Figure 1 shows the overall process of the stress-strain curves of uniaxial compression tests. As can be observed, the stress strain curves all experience a sudden drop of stress after peak, indicating a highly brittle behaviour of the material. This kind of material is hereafter termed as brittle-plastic material. To describe this phenomenon in constitutive modelling, the stress state is assumed to sharply reduce from the peak state to the residual state once it is loaded to the peak. The basic characteristics of a brittle-plastic rock overall stress-strain curve are as follows: 1) the pre-peak stress-strain curve is very linear; 2) the yielding portion before the peak is very narrow; 3) stress strain curve is ideally vertical after the peak; 4) the residual state does not experience much hardening or softening. This is different from the strain-softening model which is more gradual and has to conform to the limitation of softening rate prescribed by the classical plastic theory.
With these characteristics, the stress-strain curve of the brittle-plastic material is simplified as a ‘three-segment’ curve, as shown in Figures 1 and 2.
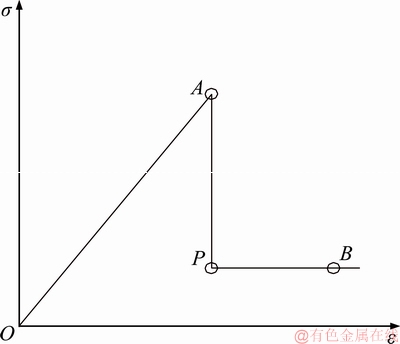
Figure 1 Ideal brittle plastic model
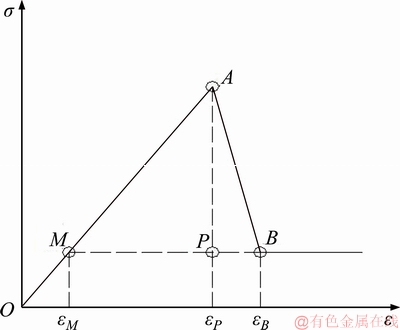
Figure 2 Non-ideal brittle plastic model
The first segment is linear-elastic. This is followed by a sharp reduction of stress. The curve plateaus after the stress drops to residual state. This model is hereafter defined as the ideally brittle-plastic material.
In reality, the drop is not ideally vertical though a very sharp (but not vertical) drop is usually involved. In such cases, the ideal brittle- plastic model is not applicable. On the other hand, the softening rate is higher than the softening rate limit prescribed by the classical plastic theory which usually leads to numerical difficulties. To account for the cases in between brittle-plastic material and traditional strain-softening material, a non-ideal brittle plastic model is proposed, as shown in Figure 2.
 (1)
(1)
where κ and α are stress-dependent variables and κ′ and α′ are their derivatives, I1 is the first stress invariant, K is the bulk modulus, G is the shear modulus.
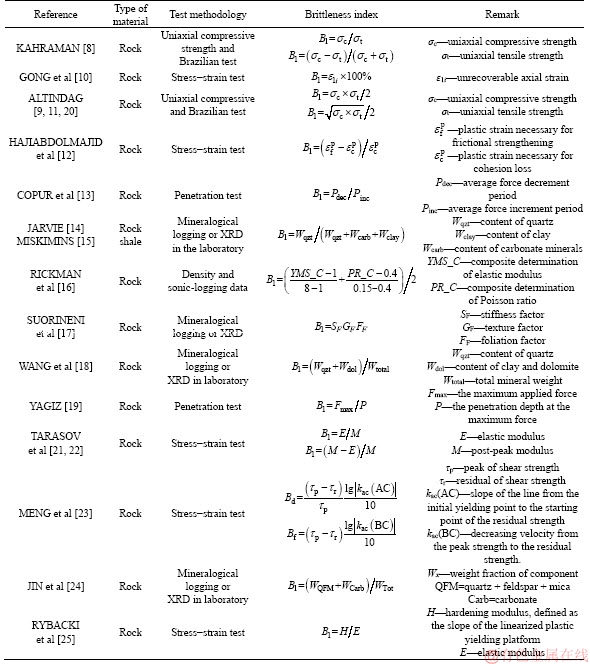
Table 1 summarizes some common approaches to describe the stress-drop effect on brittle materials.
3 Engineering approximation
During the sudden drop of stress, a non-zero strain increment Δεij is generated as Eq. (2). After evaluating the plastic flow factor λ at the peak state, one can use the following approach to approximate the sudden drop with a non-zero strain increment Δεij.
Assuming associated flow rule and we have
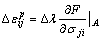 (2)
(2)
The total strain increment is the sum of elastic and plastic strain increment:
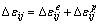 (3)
(3)
Assuming:
 (4)
(4)
where R is a positive constant describing the softening rate
 (5)
(5)
where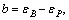
 Point B is the beginning of the residual state, as shown in Figure 3.
Point B is the beginning of the residual state, as shown in Figure 3.
From Eq. (5) we have:
 (6)
(6)
where
 (7)
(7)
Considering:
 (8)
(8)
The stress increment is:
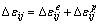 (9)
(9)
 (10)
(10)
Reformulating Eq. (10) gives:
 (11)
(11)
where
 (12)
(12)
△l can be evaluated by:
 (13)
(13)
Let  and Eq. (13) is rewritten as:
and Eq. (13) is rewritten as:
 (14)
(14)
Combining Eqs. (3) and (5) gives:
 (15)
(15)
Combining Eqs. (2), (11) and (13) gives:
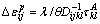 (16)
(16)
Substituting Eq. (9) into (15) and we have:
Table 1 Summary of some common approaches to describe stress-drop effect on brittle materials
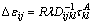 (17)
(17)
One can easily evaluate the displacement from strain via:
 (18)
(18)
The displacement increment can be obtained by substituting the strain increment calculated by Eq. (17) into Eq. (18). This displacement increment is due to the sudden drop of stress. It is then incorporated into the displacement increment in the next iteration step.
4 Experimental results of brittleness factor
The typical feature of brittle-plastic material is that it contains a mutated, uncontrollable brittle segment in stress-strain curve. And, this segment is critical for analyzing rock failure. For brittle rock, studying a reasonable method to describe this stress-drop segment after rock breaking is more realistic than ‘softening process’ analysis. Based on classical full stress-strain curve of brittle rock, a simplified curve (shown in Figure 2) is proposed by sharpening the peak region, linearizing the elastic and brittle segment and ignoring the residual stress decay. To describe the stress-drop segment in strain-stress curve, a brittleness factor R is defined. It depends on the characterising parameters (as summarised in Table 3) in curve of uniaxial and triaxial compression test, shown in Eq. (19).
 (19)
(19)
where 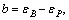
 for ideal brittle- plastic model, b=0.
for ideal brittle- plastic model, b=0.
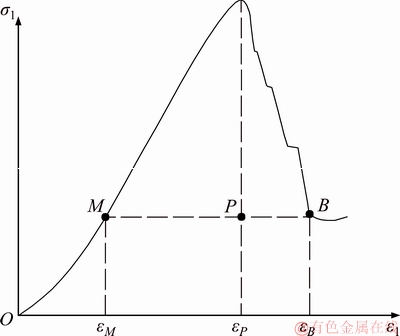
Figure 3 Sketch of stress non-vertical drop
The brittleness factor R is determined by the strain value εM, εP and εB at characteristic point M, P and B of full stress-strain curve. εP and εB could be measured directly. εM is numerically equal to residual strength σr divided by elastic modulus E, i.e. Eq. (20).
 (20)
(20)
Therefore, the brittleness factor R could be confirmed by Eq. (21).
 (21)
(21)
For triaxial compression test, the elastic module E and characterizing parameters, including σr, εP and εB, are related to confining pressure σc. As the rock would gradually become more ductile as the confining pressure increases, brittleness factor R is also varying with confining pressure. The relationship among σr, εP, εB, E, σc and R is shown in Eq. (22).
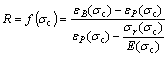 (22)
(22)
where  for isotropic compression test,
for isotropic compression test, 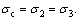
To verify the feasibility of brittleness factor R, the uniaxial compression tests and triaxial tests of red sandstone were conducted in the RMT-150B system (shown in Figure 4). The red sandstone samples were collected form Guixi, Jiangxi, and the main components by mass ratio are as following: 60% quartz, 24% feldspar, 8% calcite and 8% kaolinite. The standard size of the samples was 500 mm in diameter, 100 mm in height and 0.02 mm in surface flatness. The actual sizes would be re-measured with a caliper. Before the test, all the samples were dried for 24 h in 108 °C drying oven to eliminate the influence of water.

Figure 4 RMT-150B testing system
The natural density is 2.26 kg/m3; the dry density is 2.21 kg/m3; water content is 0.73%- 1.04%. The experiments were displacement- controlled. The strain rates were set to be 10-5 s-1 or 10-6 s-1. For triaxial test, the confining pressure ranged from 5 MPa to 40 MPa.
As the uniaxial test can be regarded as a special triaxial test with 0 MPa confining pressure, the confining pressure of triaxial tests ranges from 0 to 40 MPa. The typical full stress-strain curves of triaxial test are shown in Figure 5. The typical characteristic parameters of the test are summarised in Table 2.
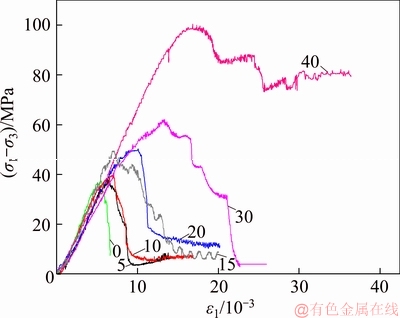
Figure 5 Typical overall stress-strain curve of normal triaxial test (Number in graph indicates confining pressure)
Based on the data in Table 2, the characterizing parameters of Red-Sandstone (shown in Table 3), can be calculated by Eqs. (23) to (26).
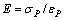 (23)
(23)
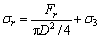 (24)
(24)
 (25)
(25)
 (26)
(26)
It can be observed from Figure 5 and Table 3 that the Red-Sandstone becomes more ductile with higher confining pressure; the peak strength would gradually increase and so does the strain at peak strength; the residual strength would increase; and the phenomenon of sharp stress-drops would no longer occur. In this case, the calculation model shown in Figure 2 would be imprecise. Then, a dual linear elastic–linear softening–residual strength calculation model is proposed shown in Figure 6. The average value of secant modulus was taken from Table 3 though a variability in observed, i.e., E=7.16 GPa. The relationships between confining pressure and characterizing parameters were analyzed with regression methods.
a) The relationship between the strain at peak strength and confining pressure
18 groups of data were used in regression analysis. The relationship between the strain at peak strength and confining pressure is shown in Eq. (27). The curve is shown in Figure 7.
 (27)
(27)
b) The relationship between the residual strength and confining pressure is obtained by applying regression methods with 18 groups of data. The formula and figure are shown in Eq. (28) and Figure 8, respectively.
 (28)
(28)
c) The relationship between the strain at residual stress point and confining pressure is shown in Eq. (29).
Table 2 Typical characterizing parameters of overall strain-stress curve of normal triaxial test
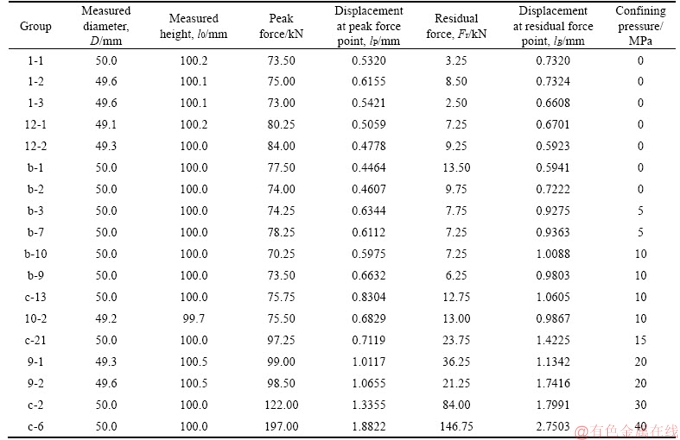
Table 3 Calculated characterising parameters of Red-Sandstone
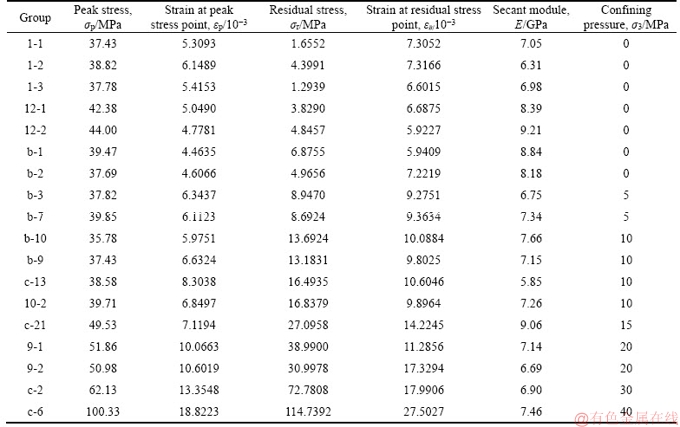
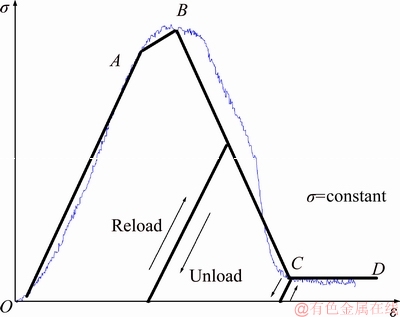
Figure 6 Dual linear elastic–linear softening–residual strength calculation model
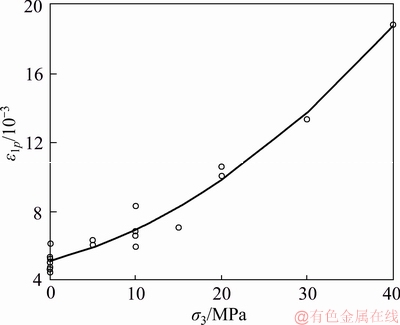
Figure 7 Relationship between strain at peak strength and confining pressure
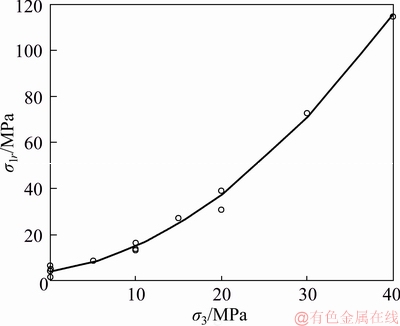
Figure 8 Relationship between residual strength and confining pressure
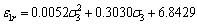 (29)
(29)
d) The relationship between the brittleness factor R and confining pressure
For triaxial test, there is a function shown in Eq. (30).
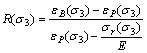
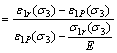
 (30)
(30)
The brittleness factor R=0.367 in uniaxial compression test.
5 Numerical analysis
The format of the stress-strain curve shown in Figure 3 was considered in finite element method, with the Tresca criterion. The calculation method of plastic flow factor is given in the Appendix. The displacement-control scheme is adopted for the numerical uniaxial test. The boundary conditions of the numerical model are those for a uniaxial test where the side of the column is free and the bottom is a set of horizontal rollers. On the other hand, the overall stress-strain curve of normal triaxial test with zero confined tests (see Figure 5) is considered as a target curve, which is simply indicated as the dashed curve in Figure 9. The main purpose of the numerical study is to validate the plastic flow factor derived in this study, as summarized in Appendix.
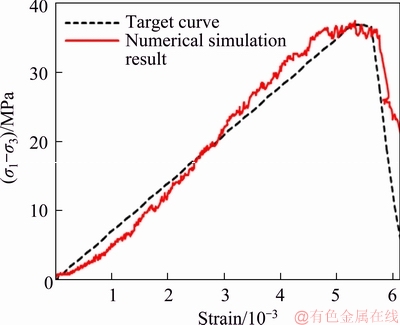
Figure 9 Numerical simulation of brittle stress drop
As shown in Figure 9, the numerical simulation result is quite similar to the target curve. At the first stage with strain from 0 to around 2.5×10-3, the stiffness of the numerical simulation is a bit lower than the target curve, while the situation is reversed for the stage with strain from 2.5×10-3 to 5×10-3. This may be attributed to the fact that the target curve is a straight line from 0 to 5×10-3, which may also not close to the real situation, as indicated in Figure 6. The remarkable feature of the numerical simulation is the stress-drop stage with strain from 5×10-3 to around 6×10-3. In this stage, the stress-drop feature is well agreeable to the target curve. This agreement validates the plastic flow factor derived in the Appendix. Figure 10 shows that plastic strain contour of the rock sample at different strain levels.
6 Conclusions
The uniaxial or triaxial compression test of cylindrical rock specimens using rock mechanics testing machine is a basic experimental method to study the strength and deformation characteristics of rock and the development process of rock fracture. In this study, experimental and numerical studies have been conducted on the stress-drop effect on the brittleness of rock materials. Calculation methods of plastic flow factors l corresponding to the four yield criteria of rock mass are proposed, including Tresca criterion, Von-Mises criterion, Mohr-Coulomb criterion and Drucker- Prager criterion. An engineering approximation approach has been proposed to evaluate the sudden drop with a non-zero strain increment. The numerical simulation results validated the effectiveness of the plastic flow factors l as well as the engineering approximation approach. Based on the results in this study, finite element code can be programmed for brittle materials with stress-drop.
Appendix
According to the four yield criteria which are widely used currently, the calculation methods of plastic flow factors l corresponding to the four yield criteria of rock mass are given.
1 Plastic flow factor l using Tresca criterion of rock blocks
Tresca criterion is the maximum shear stress criterion.
 (A1)
(A1)
where σs is the ultimate strength of uniaxial yield test.
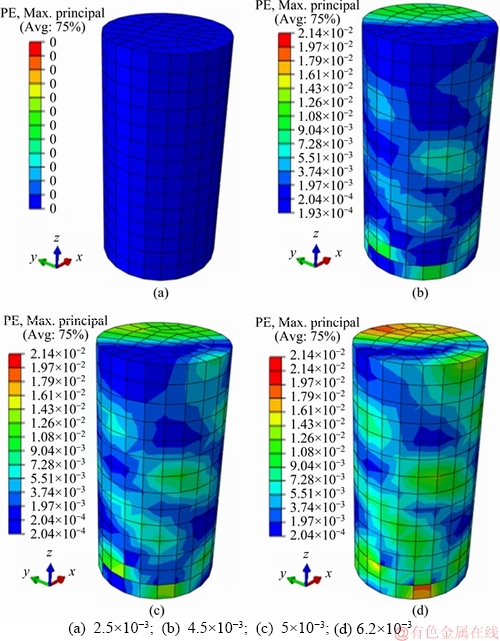
Figure 10 Plastic strain contour of rock sample at different strain levels:
The peak intensity surface and residual strength surface of rock blocks in the principal stress space are:
 (A2)
(A2)
And:
 (A3)
(A3)
 and
and  are peak intensity parameters and residual strength parameters respectively.
are peak intensity parameters and residual strength parameters respectively.
Then:
 (A4)
(A4)
Substituting Eq. (A4) into Eq. (A4) is easy to obtain:
 (A5)
(A5)
Bring Eq. (A5) into Eq. (A3):
 (A6)
(A6)
Bring Eq. (A6) into Eq. (A3):
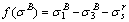
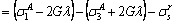
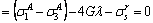 (A7)
(A7)
Combining Eq. (A2) and (A7) can easily obtain:
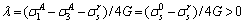 (A8)
(A8)
2 Plastic flow factor l using von-Mises criterion of rock blocks
It is assumed that the peak strength surface and the residual strength surface of rock blocks are:
 (A9)
(A9)
And:
 (A10)
(A10)
Among them,  are peak strength parameters and residual strength parameters respectively.
are peak strength parameters and residual strength parameters respectively.
Then:
 (A11)
(A11)
Bring Eq. (A11) into Eq. (A1) and we can easily get:
 (A12)
(A12)
Bring Eq. (A12) into Eq. (A1):
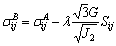 (A13)
(A13)
Bringing Eq. (A13) into J2 computational formula can get:
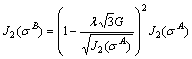 (A14)
(A14)
Bring Eq. (A14) into Eq. (A12):
 (A15)
(A15)
It is easy to get:
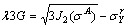
or
 (A16)
(A16)
And because of  there is:
there is:
 (A17)
(A17)
Obviously, if λ1>λ2, then λ1>0, l can be taken as:
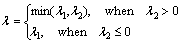 (A18)
(A18)
3 Plastic flow factor l using Mohr-Coulomb criterion of rock block
The Mohr-Coulomb criterion can be expressed as follows:
 (A19)
(A19)
If σ1≥σ2≥σ3, it can be written as:
 (A20)
(A20)
It is assumed that the peak strength plane and the residual strength plane of rock mass (described in principal stress space.) are:
 (A21)
(A21)
And:
 (A22)
(A22)
where c0, f0 and cr, fr are peak strength parameters and residual strength parameters respectively.
Then there are:
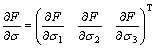
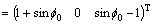 (A23)
(A23)
Bringing Eq. (A23) into Eq. (12) can easily get:
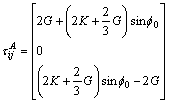 (A24)
(A24)
Bring Eq. (A24) into Eq. (11):
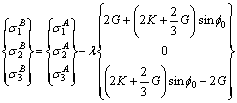
 (A25)
(A25)
Bring Eq. (A23) into Eq. (A22):
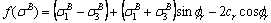
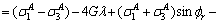
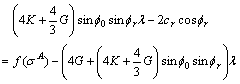
 (A26)
(A26)
Thus we can obtain:
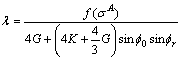 (A27)
(A27)
And:
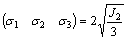
 (A28)
(A28)
Therefore, the Mohr-Coulomb criterion can be expressed as I1, J2 and θ:
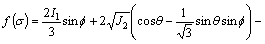
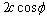 (A29)
(A29)
So:
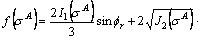
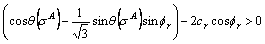 (A30)
(A30)
And:
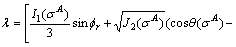
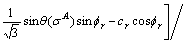
 (A31)
(A31)
4 Plastic flow factor l using Drucker-Prager criterion of rock block
It is assumed that the peak strength and residual strength of rock blocks are expressed as follows.
 (A32)
(A32)
And:
 (A33)
(A33)
where α0, κ0 and αr, κr are peak strength parameters and residual strength parameters, respectively.
Then there is:
 (A34)
(A34)
Bringing Eq. (A34) into Eq. (12) can easily get:
 (A35)
(A35)
Bring Eq. (A34) into Eq. (11):
 (A36)
(A36)
So:
 (A37)
(A37)
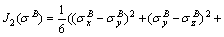
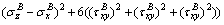
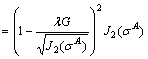 (A38)
(A38)
Bring Eqs. (A35) and (A38) into Eq. (A34) and we can get:
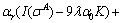
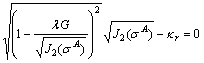 (A39)
(A39)
Then:
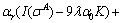
 (A40)
(A40)
Or:
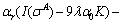
 (A41)
(A41)
That is:
 (A42)
(A42)
Or:
 (A43)
(A43)
So we can obtain that:
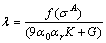
or
 (A44)
(A44)
Obviously, l can be valued according to Eq. (A18).
References
[1] TARASOV B, POTVIN Y. Universal criteria for rock brittleness estimation under triaxial compression [J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 59(4): 57-69.
[2] LABUZ J F, BIOLZI L. Experiments with rock: Remarks on strength and stability issues [J]. International Journal of Rock Mechanics & Mining Sciences, 2007, 44(4): 525-537.
[3] YANG Sheng-qi, JING Hong-wen, WANG Shan-yong. Experimental investigation on the strength, deformability, failure behavior and acoustic emission locations of red sandstone under triaxial compression [J]. Rock Mechanics and Rock Engineering, 2012, 45(4): 583-606.
[4] WONG Teng-fong, BAUD P. The brittle-ductile transition in porous rock: A review [J]. Journal of Structural Geology, 2012, 44(11): 25-53.
[5] WU Qiu-hong, LI Xi-bing, TAO Ming, DONG Long-jun. Conventional triaxial compression on hollow cylinders of sandstone with various fillings: Relationship of surrounding rock with support [J]. Journal of Central South University, 2018, 25(8): 1976-1986.
[6] ZENG Wei, YANG Sheng-qi, TIAN Wen-ling, KAI Wen. Numerical investigation on permeability evolution behavior of rock by an improved flow-coupling algorithm in particle flow code [J]. Journal of Central South University, 2018, 25(6): 1367-1385.
[7] XU Xiao-li, KARAKUS M, GAO Feng, ZHANG Zhi-wen. Thermal damage constitutive model for rock considering damage threshold and residual strength [J]. Journal of Central South University, 2018, 25(10): 2523-2536.
[8] KAHRAMAN S. Correlation of TBM and drilling machine performances with rock brittleness [J]. Engineering Geology, 2002, 65(4): 269-283.
[9] ALTINDAG R. The evaluation of rock brittleness concept on rotary blast hole drills [J]. Journal of the Southern African Institute of Mining and Metallurgy, 2002, 102: 61-66.
[10] GONG Qiu-ming, ZHAO Jian. Influence of rock brittleness on TBM penetration rate in Singapore granite [J]. Tunnelling and Underground Space Technology, 2007, 22: 317-324.
[11] ALTINDAG R. The role of rock brittleness on analysis of percussive drilling performance [C]// Proceedings of 5th National Rock Mechanics. Turkish, 2000:105-112.
[12] HAJIABDOLMAJID V, KAISER P. Brittleness of rock and stability assessment in hard rock [J]. Tunneling and Underground Space Technology, 2003,18(1): 35-48.
[13] COPUR H, BILGIN N, TUNCDEMIR H, BALCI C. A set of indices based on indentation tests for assessment of rock cutting performance and rock properties [J]. Journal of the Southern African Institute of Mining and Metallurgy, 2003,103(9): 589-599.
[14] JARVIE D M, HILL R J, RUBLE T E POLLASTRO R M. Unconventional shale-gas systems: The Mississippian Barnett Shale of north-central Texas as one model for thermo genic shale-gas assessment [J]. AAPG Bull, 2007, 91(4): 475-499.
[15] MISKIMINS J L. The impact of mechanical stratigraphy on hydraulic fracture growth and design considerations for horizontal wells [J]. Bulletin, 2012, 91: 475-499.
[16] RICKMAN R, MULLEN M, PETRE J, GRIESER W V, KUNDERT D. A practical use of shale petro-physics for stimulation design optimization: all shale plays are not clones of the barnett shale [C]// Presented at the SPE Anuual Technical Conference and Exhibition. Denver, Colorado, 2008, September. SPE-115258.
[17] SUORINENI F T, CHINNASANE D R, KAISER P K. A procedure for determining rock-type specific Hoek-Brown brittle parameters [J]. Rock Mechanics Rock Engineering, 2009, 42(6): 849-881.
[18] WANG F P, GALE J F W. Screening criteria for shale-gas systems [J]. Gulf Coast Association of Geological Societies Transactions, 2009, 59: 779-793.
[19] YAGIZ S. Assessment of brittleness using rock strength and density with punch penetration test [J]. Tunneling and Underground Space Technology, 2009, 24(1): 66-74.
[20] ALTINDAG R. Assessment of some brittleness indexes in rock drilling efficiency [J]. Rock Mechanics Rock Engineering, 2010, 43(3): 361-370.
[21] TARASOV B G, POTVIN Y. Absolute, relative and intrinsic rock brittleness at compression [J]. Mining Technology, 2012, 121(4): 218-225.
[22] TARASOV B G, POTVIN Y. Universal criteria for rock brittleness estimation under triaxial compression [J]. International Journal of Rock Mechanics and Mining Science, 2013, 59(4): 57-69.
[23] MENG Fan-zhen, ZHOU Hui, ZHANG Chuan-qing, XU Rong-chao, LU Jing-jing. Evaluation methodology of brittleness of rock based on post-peak stress–strain curves [J]. Rock Mechanics Rock Engineering, 2015, 48(5): 1787-1805.
[24] JIN Xiao-chun, SHAH S N, ROEGIERS J C, ZHANG Bo. An Integrated petrophysics and geomechanics approach for fracability evaluation in shale reservoirs [J]. SPE Journal, 2015, 20(3): 518-526.
[25] RYBACKI E, MEIER T, DRESEN G. What controls the mechanical properties of shale rocks? –Part II: Brittleness [J]. Journal of Petroleum Science and Engineering, 2016, 144(8): 39-58.
(Edited by HE Yun-bin)
中文导读
应力降对岩石材料脆性评价的影响
摘要:利用岩石力学试验机对圆柱岩石试样进行单轴和三轴压缩试验,是研究岩石强度和岩石裂隙发展过程的基本试验方法。针对岩石材料应力降效应的问题,首先进行了广泛的文献调研;然后,分别利用室内试验和数值模拟的方法,研究了应力陡降效应对岩石类材料脆性特征的影响。为了描述应力降效应,本文提出了塑性流变因λ,且基于Tresca准则、Von-Mises准则、Mohr-Coulomb准则和Drucker- Prager准则等四类岩体屈服准则,对塑性流变因子λ进行了评价。此外,为了简便,在非零应变增量下,提出利用工程近似方法研究应力降。研究结果表明:数值模拟和工程近似方法均验证了塑性流变因子的有效性;脆性材料的应力降,可以通过有限元代码编码实现,且该代码可以与原有限元代码简单有效融合。
关键词:岩石类材料;应力陡降效应;塑性流变因子;强度准则
Foundation item: Projects(51678083, 41302226) supported by the National Natural Science Foundation of China
Received date: 2019-03-13; Accepted date: 2019-05-29
Corresponding author: PAN Yu-tao, PhD; Tel: +65-86516478; E-mail: ceepany@nus.edu.sg; ORCID:0000-0001-9504-1347; YANG Xiao-li, PhD, Professor; E-mail: yangky@ aliyun.com