J. Cent. South Univ. (2012) 19: 1040-1048

DOI: 10.1007/s11771-012-1107-1

Color image segmentation using mean shift and improved ant clustering

LIU Ling-xing(刘玲星)¹, TAN Guan-zheng(谭冠政)¹, M. Sami Soliman¹

1. of Information Science and Engineering, Central South University, Changsha 410083, China;

2. National Research Institute of Astronomy and Geophysics, Helwan 11421, Egypt

? Central South University Press and Springer-Verlag Berlin Heidelberg 2012

Abstract: To improve the segmentation quality and efficiency of color image, a novel approach which combines the advantages of the mean shift (MS) segmentation and improved ant clustering method is proposed. The regions which can preserve the discontinuity characteristics of an image are segmented by MS algorithm, and then they are represented by a graph in which every region is represented by a node. In order to solve the graph partition problem, an improved ant clustering algorithm, called similarity carrying ant model (SCAM-ant), is proposed, in which a new similarity calculation method is given. Using SCAM-ant, the maximum number of items that each ant can carry will increase, the clustering time will be effectively reduced, and globally optimized clustering can also be realized. Because the graph is not based on the pixels of original image but on the segmentation result of MS algorithm, the computational complexity is greatly reduced. Experiments show that the proposed method can realize color image segmentation efficiently, and compared with the conventional methods based on the image pixels, it improves the image segmentation quality and the anti-interference ability.

Key words: color image segmentation; improved ant clustering; graph partition; mean shift

1 Introduction

Image segmentation is a process that partitions an image into different regions so that each region is nearly homogeneous, whereas the union of any two regions is not [1]. The purpose of image segmentation is to make images easily understood and analyzed by simplifying or changing their representation forms. The results are sets of image promoter regions (all of these branch regional areas cover the entire image), or collections of the profiles extracted from the image. It is a vital step in the image analysis chain with applications on pattern recognition, clinical and medical studies [2], object detection and tracking, and other computer-vision related applications.

So far, image segmentation methods can be roughly classified into three categories: feature-space [3-4] based clustering, spatial segmentation and graph-based partitioning. The first approach [5-6] captures the global characteristics of image through the selection and calculation of the image features, such as color and texture. Although the data clustering approaches are very efficient in finding salient image features, they have some drawbacks as well. For example, they cannot preserve the spatial structure and the detailed edge information of image, and pixels from disconnected regions may be grouped together if the feature space is overlapped. The spatial segmentation method is referred to be region-based when it is based on region entities too. Graph-based approaches [7-8] can be regarded as image perceptual grouping and organizational methods which are based on the fusion of future and spatial information. GRADY and SCHWARTZ [8] introduced an alternative method which founds partitions with a small isoperimetric constant. The common theme of these approaches is the formation of a weighted graph, and the weights are usually related to the color and the spatial characteristics of the corresponding pixels or regions. Each vertex in the graph corresponds to an image pixel, and the weight of each edge connecting two pixels represents the likelihood they belong to the same segment. The segmentation performance of graph-partitioning approach is sensitive to the graph grouping strategy and the region segmentation results.

In recent years, normalized cut (Ncut) algorithm has caught researcher’s extensive concern. It has been empirically shown that the Ncut algorithm can generate balanced clusters robustly and is also superior to other spectral graph-partitioning methods. However, it has some drawbacks when it is applied to segmentation. Because the Ncut method is based on the pixels of whole image, and it requires high computation complexity in general and is sensitive to the noise, it is not suitable for real-time processing and the performance after segmentation of the image usually is not very good [9].

To overcome these weaknesses, a novel approach called similarity carrying ant model (SCAM-ant) was proposed, which provides robust and effective image segmentation with low computational complexity by incorporating the mean shift (MS) method and improved ant clustering. This method applies MS which is based on the color information of the image for preliminary segmentation, and then it segments the image into distinct scenes by SCAM-ant algorithm.

2 MS and construction of graph

2.1 MS for image region segmentation

The MS algorithm is a nonparametric iteration method [10] based on the increased gradient density. It finds the position of target and realizes the target tracking through iterative computation. The outstanding advantages are small computations, which are simple and easy to realize. The MS algorithm has obtained successful applications in many fields, such as image smoothing, segmentation, and target tracking. It can significantly reduce the number of basic image entities, and because of the good discontinuity preservation filtering characteristic, the salient features of the image are retained. This property is very important in the partitioning of natural images, because only several distinct regions are used in representing different scenes such as the lake, sky and animals in natural images, whereas other information is often less important and can be neglected. However, it also has some faults. It is difficult to be used in partitioning a natural image into meaningful regions that represents distinct scenes depending only on the MS segmentation. The main reason is that the MS is an unsupervised clustering-based method, where the shape and the number of the data clusters are an unknown priori. Moreover, the end of the segmentation process is based on some region-merging strategies which are applied to the filtered image result, and the number of regions after segmentation are mostly determined by the minimum number of pixels, denoted in a region by M. Regions containing less than M will be eliminated and merged into its neighboring region. So, the boundary information of the last segmented image is retained by the boundaries of regions [11].

Symmetric kernels are considerably satisfied for  where the constant c_k,d>0 is selected so that  (Note that k(x) is defined only for x≥0). k(x) which is referred to as the profile of the kernel is a monotonically decreasing function, and the kernel G(x) is defined as G(x)=c_g,dg(||x||²). For n points x_i, i=1, …, n, in the d-dimensional space R^d, the MS algorithm is defined as

                    (1)

where x is the center of the kernel, and h is a bandwidth parameter. Therefore, the MS algorithm which uses kernel G as the weight and x as the center of kernel is different from the weighted mean.

The MS method is guaranteed to converge to a nearby point where the estimate has a zero gradient. Regions of high-density values are of more interest for feature-space analysis, and in such regions, the MS steps are small. On the other hand, the steps are large, and there is no analysis. The MS procedure is an adaptive gradient ascent method and the center position of kernel G can be updated iteratively by

 (j=1, 2, …)           (2)

where y_j is the center of initial position of kernel. The MS image filtering algorithm can be obtained based on the analysis in Eq. (2). First, an image is represented as a two-dimensional (2D) lattice of p-dimensional vectors, where p>3 for multispectral images, p=3 for color images and p=1 for gray-level images. The graph level and the color of spectral information are then represented in the range domain, while the space of the lattice is known as the spatial domain. For both domains, the Euclidean metric is assumed. Let the representations of pixels be the d-dimensional (d=p+2) input and the filtered image pixels in the joint spatial-range domain.

The MS segmentation is actually a merging process performed on a region that is produced by the filtering. Here, it is needed to select the bandwidth parameter h= (h_r, h_s) which determines the resolution of mode detection by controlling the size of kernel. Parameter h_r is the rang bandwidth and h_s is the space bandwidth. Figure 1 contains the image whose size is 184 × 271 after MS preliminary segmentation, h=(h_r, h_s)=(6, 8) and M=1 000 have been set. It is obvious that the image has been divided into 15 different pieces of area according to the color feature of original image. Different regions are represented by different colors in the image segmented by MS algorithm.

2.2 Graph construction

After segmentation, the image is divided into several regions using MS algorithm and each region is represented by a node. In order to convert image segmen- tation into graph partition, firstly, it is necessary to construct a non-directed and weighted graph G=(v, e) which consists of a set of vertices v and a set of edges e so that each edge is a subset of two vertices in v [12]. The weight w(u, v) of edge connecting two vertices u and v in the graph reflects the similarity degree of image. It can be extracted by position, color and texture features of image [13].

Fig.1 Original image (a), result image after using MS algorithm (b),  contour images of final region- merging results using proposed method (c), original images overlapped with contour of final region-partitioning results (d) and partitioning results by directly applying Ncut method to image pixels (e)

In this work, the color feature is adopted as the measure of dissimilarity between neighboring regions. This is because it is usually the most dominant and distinguishing visual feature that is adequate for a number of segmentation tasks. The average color components are described by a three-element color vector and are computed over pixels of a region. When an image is segmented into n regions R_i, i=1, …, n, based on MS method, for each region, the mean vector  is computed, where   and  are the mean pixel intensities of the i-th region in three different color spaces, respectively.

To obtain meaningful segmentation results, the perceived color difference should be associated with the Euclidean distance in the color space. The spaces (L, U, V) have been particularly designed to approximate the perceptually uniform color spaces. The weight matrix W of all regions resulting from the definition of color space is computed. The weight w(u, v) between regions u and ν is defined

    (3)

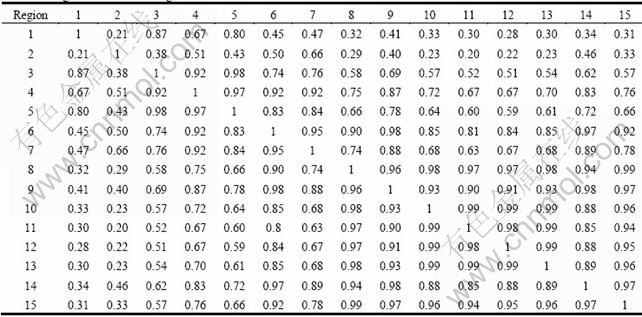
where ||·||₂ denotes the vector norm operator, and F(u)={L(u), U(u), V(u)} is the color vector of region u. In addition, d_I is a positive scaling factor which determines the sensitivity of w(u, v) to the color difference between the nodes u and ν. From Fig. 1(b), the weight matrix W of all region nodes is computed and the results are summarized in Table 1.

Through the above analysis, an image after MS segmentation is represented by a graph, and image segmentation problem is therefore converted into a graph partition problem. The SCAM-ant method is used to perform this conversion. Unlike in other conventional image segmentation methods, the weight matrix of the method in this work is not based on the pixels of original image but on the segmentation result of MS algorithm. Using regions of the image instead of pixels to construct the weight matrix has many advantages. One is that since the number of basic image entities is much smaller than that of pixels, the computational complexity of image is considerably reduced. Thus, the size of the weight matrix and the complexity of the graph structure which represents the image are likewise significantly reduced. Moreover, after a natural image is segmented into regions, the pixel value within each segment approximately depends on a one-dimensional RGB space according to the physical characteristics of the image. This important fact helps to significantly reduce the color noise. The MS method not only removes this noise (which limits the accuracy of graph partitioning in the SCAM-ant algorithm) but also adaptively reduces the amount of smoothing for the abrupt changes in the edges and retains the salient features of the overall image.

Table 1 Weight matrix W of all region nodes

3 Graph partition using improved ant clustering

Graph-based image segmentation method is a new research area and many scholars have put forward different optimal graph partitioning rules for image segmentation. Notable examples included the normalized cut, isoperimetric cut, and k-means [14]. These rules, which are very sensitive to initial conditions, are applied to segmentation generally based on data clustering of the image pixels directly, and the computation increases with the increase of image size [15]. Many researchers have proposed the use of evolutionary algorithms in graph partitioning. This work presents a new method which can effectively solve graph partition problems.

3.1 Introduction of improved ant clustering

Clustering algorithms that draw their inspiration from ant’s behavior observed in nature and its application in graph portioning have been reviewed in Ref. [16]. The first ant-based clustering algorithm was introduced by DENEUBOURG et al [17]. Then, KUNTZ et al [18] proposed use of ant clustering in graph partitioning. The KLS algorithm [18] considers the problem of a graph partitioning through embedding into a plane or Euclidian space. The ant-based clustering model is essentially a dynamical system where vertices are attracted to or rejected by clusters according to the distance between them. A novel ant-based algorithm called SCAM-ant is proposed in this work. Under SCAM-ant, each ant has the probability of carrying more items while it moves around. The decision is governed by the candidate item and the similarity of carried items. The SCAM-ant method makes use of the group items moving behavior to reduce time instead of single item moving in the original ant clustering algorithm.

3.1.1 Similarity measurement using modified SimRank

SimRank [19] is an algorithm for analyzing the graphs derived from data sets to compute similarity scores based on the structural context in which they appear. According to the SimRank, a solution to a graph G can be reached by iteration to a fixed-point. Let n be the number of nodes in graph G. For each iteration k, it can keep n² entries R_k(_*, _*) of length n², where R_k(a, b) gives the score between a and b on iteration k. It successively computes R_k+1(_*, _*), and based on R_k(_*, _*) starting with R₀(_*, _*).

                     (4)

where w(a, b) is the weight of edge between a and b. Then, from R_k(_*, _*), when a≠b, R_k+1(a, b) can be gotten:

     (5)

And R_k+1(a,b)=1 for a=b. The values R_k(_*, _*) are non-decreasing as k increases. The SimRank is combined with the weight to get the final similarity measurement.

The form of the dissimilarity between two nodes in the weighted graph can be calculated by

              (6)

where R₆(v_i, v_j) is the result of the 5th SimRank iteration.

The local density f(v_i) is calculated as

          (7)

where  is the computation cost for the operator v_i.  So, the density function is the summation of the difference between operator v_i and all other objects in neighbourhood L of v_i. It represents the concentration of the similarity scaled with the total computation cost of the neighbour operators.

3.1.2 Similarity carrying ant model (SCAM)

The ants clustering algorithm has been inspired from the biological life of ants in nature, so its modification should also be the inspired form of their life. As is known, an ant can lift 20-50 times its own body weight. This fact is useful in enhancing the performance of the ant clustering [20]. Under SCAM, the probability of carrying more items is governed by the similarity of carried items and the candidate item. The similarity can be measured by the average distances as

                           (8)

where N_c is the number of items carried by the ant and C is the carried items set. If the similarity value S_m(v) is less than similarity threshold, the ant carries the nominated item with other items. The value of similarity threshold can be calculated by sorting the intra-distances between all items. In this way, the group picking and dropping behaviour reduces the number of ant movements, with the purpose of reducing the time for the complete clustering process.

3.2 Process of clustering using SCAM-ant

The two probabilities closely related to the clustering process are the probability of picking up an object P_pick(v_i) and that of dropping P_drop(v_i), as

                       (9)

                     (10)

where the parameter k₁∈[0,1] controls the pick-up sensitivity, and the constant k₂ governs the drop sensitivity. Once each ant is holding an object, the main loop of the algorithm begins.

The process of clustering using SCAM-ant is as follos.

Step 1: Initialization. Convert optimized query plan into query graph and compute dissimilarity δ(v_i, v_j) for all vertices in the graph using Eq. (6). Place every vertex v_i and agents randomly.

Step 2: For all agents, if agent can carry more and the site is occupied by vertex v_i, then compute f(v_i) using Eq. (7), P_pick(v_i) using Eq. (9) and S_m(v_i) using Eq. (8). Draw random real number R between 0 and 1, and continue. Otherwise, go to Step 4.

Step 3: If R

pick(v_i), the agent is empty or already carries items and S_m(v_i) is not bigger than similarity threshold, then pick up item v_i, and go to Step 8.

Step 4: For every carried item v_i, if the agent is carrying items and the site is empty, then compute f(v_i) using Eq. (7), and compute P_drop(v_i) using Eq. (10).

Step 5: Draw random real number R between 0 and 1.

Step 6: If Rdrop(v_i)), then drop item v_i where P_drop(v_i)=Max(P_drop(v_i)).

Step 7: Move to randomly selected neighboring site not occupied by other agents.

Step 8: Finalization. All agents drop all carried items in agent locations or nearest free locations.

The result of graph partitioning using SCAM-ant is shown in Fig. 1(c). It is clearly observed that there are only four clusters. The outlines of the hill have been largely segmented out. Figure 1(e) is the result due to segmentation by Ncut [21]. By comparing the two  results, it can be noted that the method presented is significantly more feasible than the Ncut algorithm.

4 Experimental results and analysis

To clearly show the feasibility of the model, the proposed algorithm was applied to the segmentation of a set of scenes of natural color images. The size of each image in the experiments is 200 × 150. The parameters h_r, h_s, k₁, k₂, M and α are set to be 6, 8, 0.3, 0.1, 1 000 and 1, respectively. The maximum number of items that each ant can carry for SCAM-ant is set to be 3, the grid size is 10×10 and the experimental environment is MATLAB R2008a. The contrastive experiment results using the isoperimetric algorithm and the Ncut method implemented by COUR et al [21] are presented for comparison. The MATLAB code for the isoperimetric algorithm which has the stop parameter p_stop and the free parameter β can be found at http://eslab.bu.edu/software/ graphanalysis/(in the Graph Analysis Toolbox).

4.1 Comparison of image segmentation results

The experiments on color images with natural scenes were carried out using the proposed method and the obtained segmentation results were presented. Figure 2 shows some selected typical comparative results based on the isoperimetric algorithm and the conventional Ncut.

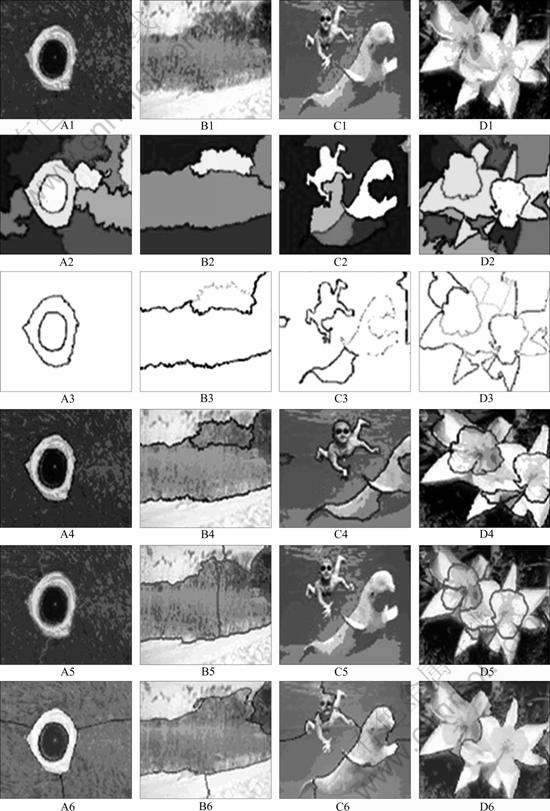
Fig. 2 Test results of color images from natural scenes (A, B, C and D represent four different figure series; Number 1 represents original test images; Number 2 represents region segmentation results by MS algorithm; Number 3 represents contour images of final region-merging results using SCAM-ant; Number 4 represents original images overlapped with contour of final region-partitioning results; Number 5 represents segmented results by applying isoperimetric algorithm using parameters (β=95, p_stop=1×10^-5), which are the same as Ref. [8]; Number 6 represents segmented results by directly applying Ncut method to image pixels)

From Fig. 2, it can be observed that the proposed method is obviously superior to the isoperimetric algorithm, and the Ncut method on segmentation results with different number of regions. For example, from the segmentation results of the animal’s eye in the first column, we can clearly get the outlines of the eye using the proposed method, but we get some redundant parts using the isoperimetric algorithm and the Ncut method. Likewise, in the segmentation results of the child in the third column, using the proposed method we can get distinct outlines of the child; however, the results segmented by the Ncut method has little relation to the profile of the child and there is no segmentation result using the isoperimetric algorithm. There is significant contrast between the three methods, as shown in Fig. 2.

4.2 Comparison of anti-interference ability

Images with natural scenes are generally interfered by noise to different levels. Therefore, the ability of anti-interference is an important index on evaluating image processing method. We applied the proposed algorithm for the segmentation of images interfered by increasing amounts of additive noise and compared them with the isoperimetric algorithm and the conventional Ncut. Results of this experiment are shown in Fig. 3. The experimental environment and parameters are the same as before.

Fig. 3 Test results of color images with increasing amounts of additive noise (Top row is segmentation of image with no noise; First column represents color images with increasing amounts of additive noise; Second column represents segmented results using proposed method; Third column represents segmented results using isoperimetric algorithm, underlying graph topology was four-connected lattice and β=95, p_stop=1×10^-5; Fourth column represents segmented results using Ncut algorithm)

Table 2 Comparison of computation efficiency using proposed method, isoperimetric algorithm and Ncut algorithm

In the comparison, additive noise was used to test the sensitivity of the three algorithms to noise. The additive noise was zero-mean Gaussian noise with variance ranging from 1%-20% of the brightest luminance. Because the proposed segmentation method combined with MS is based on the color feature of regions in the image which is almost not influenced by the feature of a single pixel, it can effectively remove the interference of noise. From the last three columns of the figures, we can see that, the results of image segmentation using the proposed method are almost not affected by the noise. On the contrary, the results by the Ncut method and the isoperimetric algorithm are seriously affected by the noise. So, the proposed segmentation method obviously has stronger anti-interference ability compared with the other two segmentation algorithms.

4.3 Comparison of computation efficiency

As conventional segmentation methods are based on the pixels of the image, the computation of the algorithms increases rapidly with the increase of image size. But since the proposed method is based on the results segmented by MS, the number of regions in the processed object is much fewer than that of the image pixels, so the computation efficiency of the proposed method is significantly increased. The segmentation time of Fig. 2 for each method is listed in Table 2. A personal computer, which is equipped with a 1.86 GHz Pentium CPU and 0.99 GB memory, is used. From the data in Table 2, it can be concluded that when we apply the three methods to the segmentation of the same image, the proposed method is slower than the isoperimetric algorithm but much faster than the Ncut.

5 Conclusions

1) A new graph partition algorithm called SCAM- ant has been developed and combined with the MS method to realize color image segmentation. Compared with the original KLS algorithm used for graph partitioning, the SCAM-ant method provides a new similarity calculation method and improves the maximum number of items that each ant can carry, thus significantly shortening the clustering time.

2) The application of the MS method allows for the formation of segments that preserve discontinuous characteristics of an image. At the same time, the application of the region adjacent graph and SCAM-ant to the resulting segments, rather than directly to the pixels of the image, yields superior image segmentation results.

3) The experiments and analyses demonstrate that the proposed method has stronger anti-interference ability compared with the isoperimetric algorithm and the conventional Ncut method. The computation complexity of the image using the proposed method is also considerably reduced, and therefore it has wide application prospects.

References

[1] VIJAYA G, DR VASUDEVAN V. A simple algorithm for image denoising based on ms segmentation [J]. International Journal of Computer Applications, 2010, 2(6): 9-10.

[2] LEE Juin-der, SU Hong-ren, CHENG P E, LIOU M, ASTON J A D, TSAI A C, CHEN Cheng-yu. MR image segmentation using a power transformation approach [J]. IEEE Transactions on Medical Imaging, 2009, 28(6): 894-905.

[3] FARMER M E, JAIN A K. A wrapper-based approach to image segmentation and classification [J]. IEEE Transactions on Image Processing, 2005, 14(12): 2060-2072.

[4] MAKROGIANNIS S, ECONOMOU G, FOTOPOULOS S. A region dissimilarity relation that combines feature-space and spatial information for color image segmentation [J]. IEEE Transactions on Systems, Man, and Cybernetics-Part b: Cybernetics, 2005, 35(1): 44-53.

[5] JACOBS D W, WEINSHALL D, GDALYAHU Y. Classification with nonmetric distances: Image retrieval and class representation [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(6): 583-585.

[6] AWAD M, CHEHDI K, NASRI A. Multicomponent image segmentation using a genetic algorithm and artificial neural network [J]. IEEE Geoscience and Remote Sensing Letters, 2007, 4(4): 571-575.

[7] LE T H, JUNG S W, CHOI K S, KO S J. Image segmentation based on modified graph-cut algorithm [N]. Electronics Letters, 2010-8-5, 46(16).

[8] GRADY L, SCHWARTZ E L. Isoperimetric graph partitioning for image segmentation [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2006, 28(3): 469-475.

[9] SHI Jian-bo, MALIK J. normalized cuts and image segmentation [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(8): 888-905.

[10] LI Xiang-ru, WU Fu-chao, HU Zhan-yi. Convergence of a Mean Shift algorithm [J]. Journal of Software, 2005, 6(3): 365-374. (in Chinese)

[11] TAO Wen-bing, JIN Hai, ZHANG Yi-min. Color image segmentation based on Mean Shift and normalized cuts [J]. IEEE Transactions on Systems, Man, and Cybernetics—Part b: Cybernetics, 2007, 37(5): 1382-1389.

[12] LENG Ming, YU Song-nian, DING Wang, GUO Qiang. An effective multi-level algorithm based on ant colony optimization for graph bipartitioning [J]. Shanghai Univ (Engl Ed), 2008, 12(5): 426-432.

[13] SUN Liang, WANG Xi-chang, LIU Jiang. Method of document image segmentation based on ncut [J]. Information Technology and Informatization, 2008(6): 93-95. (in Chinese)

[14] ISA A M, SALAMAH S A, NGAH U K. Adaptive fuzzy moving k-means clustering algorithm for image segmentation [J]. IEEE Transactions on Consumer Electronics, 2009, 55(4): 2145-2153.

[15] YAN Cheng-xin, SANG Nong, ZHANG Tian-xu. Image segmentation by graph partition on histogram clustering [J]. Computer App locations, 2005, 25(3): 570-572. (in Chinese)

[16] HAND J, MEYER B. Ant-based and swarm-based clustering [J]. Swarm Intelligence, 2007, 1(1): 95-113.

[17] DENEUBOURG J L, GOSS S, FRANKS N, SENDOVA-FRANKS A, DETRAIN C, CHR?TIEN L. The dynamics of collective sorting robot-like ants and ant-like robots [C]// Proceedings of the First International Conference on Simulation of Adaptive Behavior on from Animals to Animats. Cambridge, MA, USA, 1990: 356-363.

[18] KUNTZ P, LAYZELL P, SNYERS D. A colony of ant-like agents for partitioning in VLSI technology [C]// HUSBANDS P, HARVEY I, ed. Proceedings of Fourth European Conference on Artificial Life. Brighton, UK, 1997: 417-424.

[19] Glen Jeh, Jennifer Widom. SimRank: A measure of structural-context similarity [C]// Proceedings of the Eighth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Alberta, Canada, 2002: 538-543.

[20] SAMI SOLIMAN M, TAN Guan-zheng. Graph partitioning using improved ant clustering [C]// TAN Y, SHI Y, TAN K C, Eds. The International Conference on Swarm Intelligence 2010: Part I. Lecture Notes in Computer Science(LNCS)6145, The International Conference on Swarm Intelligence. Beijing, China, 2010: 231-240.

[21] COUR T, YU S, SHI J. Normalized cuts matlab code [EB/OL]. [2010-11-23]. http://www.cis.upenn.edu/~jshi/software.

(Edited by DENG Lü-xiang)

Foundation item: Project(60874070) supported by the National Natural Science Foundation of China

Received date: 2011-01-28; Accepted date: 2011-05-03

Corresponding author: TAN Guan-zheng, Professor, PhD; Tel: +86-731-85863436; E-mail: tgz@csu.edu.cn