DOI: 10.11817/j.issn.1672-7207.2016.05.042
基于稀疏正则化的内外置电极电容层析成像
毛明旭1, 2,叶佳敏1,王海刚1,邱桂芝1, 2
(1. 中国科学院 工程热物理研究所,北京,100190;
2. 中国科学院大学 物理学院,北京,100190)
摘要:利用一种基于软阈值的稀疏正则化图像重构算法,对IEE ECT内部的介质分布进行重构,并与Landweber迭代算法进行对比。仿真和实验结果表明:对于内外置电极的ECT,基于软阈值的稀疏正则化重构算法可以明显减少迭代步数,提高重构图像的质量。
关键词:电容层析成像;内外置电极;图像重构;稀疏正则化;软阈值
中图分类号:TP216 文献标志码:A 文章编号:1672-7207(2016)05-1774-08
Sparse regularization based image reconstruction for electrical capacitance tomography with internal-external electrodes
MAO Mingxu1, 2, YE Jiamin1, WANG Haigang1, QIU Guizhi1, 2
(1. Institute of Engineering Thermophysics, Chinese Academy of Sciences, Beijing 100190, China;
2. College of Physics, University of Chinese Academy of Sciences, Beijing 100190, China)
Abstract: A sparse regularization algorithm based on a soft-thresholding function was employed in the image reconstruction for IEE ECT and compared with Landweber iterative algorithm quantitatively. Both numerical simulation and experimental study show that the sparse regularization algorithm can significantly reduce the number of iteration and improve the quality of the reconstructed images for IEE ECT.
Key words: electrical capacitance tomography; internal-external electrodes; image reconstruction; sparse regularization; soft-thresholding
电容层析成像(ECT)是一种断面成像技术,根据被测对象介电常数的不同来重构其内部物质的浓度分布。ECT技术由于其具有无辐射、成像速度快、非接触和非侵入、耐高温高压和成本低等优点[1],目前已经广泛应用于不同领域的测量过程中,包括原油管道中的油/气两相流[2]、火焰[3]、气力输送[4-5]和循环流化床内气固两相流[6]等。在制药过程中,Wurster流化床常被应用于颗粒包衣过程。Wurster流化床床内中心区域放置有导向管,导向管的存在可以规范颗粒运动轨迹,使颗粒表面形成均匀、一致的包衣涂层。这样在导向管和外管之间形成一个环形区域,此区域内颗粒浓度分布的在线监测对于提高设备运行效率、获取高质量产品尤为重要。而常规的具有外置电极的ECT传感器由于中心区域灵敏度低,因此难以准确监测环形区域的物质分布[7]。一些研究人员提出了内外置结构的电极(IEE)来提高中心区域的灵敏度。若将具有内外置电极的ECT传感器应用到上述过程中,则有助于研究环形区域的物质分布,提高过程效率[7]。ECT图像重构是一个典型的病态问题,因此,在利用IEE ECT进行测量的过程中,除了测量得到的电容,图像重构算法也至关重要。ECT图像重构算法分为非迭代算法和迭代算法。在非迭代算法中,XIE等[8]提出了LBP算法,LBP算法速度快但成像质量较差,一般用于定性分析。在迭代算法中,YANG等[9]提出了Landweber迭代算法,此算法可以得到质量较高的图像,但若要实现在线测量,则必须限制迭代步数,从而影响成像质量。PENG等[10]研究了Tikhonov正则化在ECT图像重构中的应用,LEI等[11]比较了ART算法,SIRT算法和OIOR算法等对图像重构质量的影响。目前,LBP算法和Landweber迭代算法应用最为广泛。0范数是一种常见的对信号实施稀疏性约束的方法。如果解足够稀疏,则0范数问题和1范数问题具有相同解[12]。目前常用的提高稀疏性的方法包括wavelet变换[13]、ridgelets变换[14]、curvelets变换[15]、Fourier变换和奇异值分解法(SVD)[16]等。YE等[17]提出了一种基础扩展敏感场的稀疏重构方法,并利用仿真和实验研究验证了算法的性能。此外,DAUBECHIES等[16]认为1范数迭代算法相当于带有软阈值函数的Landweber迭代算法,并给出了理论分析结果。基于此,JIN等[18]提出了一种适用于EIT的图像重构算法。DONG等[19]提出了一种适用于ECT的带有合适正则化参数的软阈值迭代算法,结果表明该算法所重构的图像与Landweber算法所得图像质量相近,但大多数情况下该算法所需时间更短。基于此原理,YE等[20]提出了一种基于软阈值的稀疏正则化重构算法,并且在具有外置电极的ECT传感器上进行了仿真和实验验证,结果表明此算法对于具有外置电极的ECT传感器具有良好的重构效果。本文作者利用Ye等[20]提出的基于软阈值的稀疏正则化图像重构算法,对具有内外置电极的ECT传感器进行数值仿真和实验测试,研究此算法在内外置电极ECT图像重构中的性能。
1 ECT线性模型简介
ECT的归一化线性模型可以表示为[8]
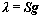
其中: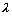 为归一化电容向量;S这归一化敏感场矩阵;g为归一化介电常数向量。
为归一化电容向量;S这归一化敏感场矩阵;g为归一化介电常数向量。
敏感场矩阵元素采用下式计算[8]:
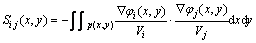
其中: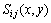 为电极i和电极j在区域
为电极i和电极j在区域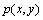 上的灵敏度;
上的灵敏度;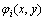 为指电极i上施加激励电压
为指电极i上施加激励电压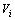 ,同时其他电极接地时的电势。
,同时其他电极接地时的电势。
对于有噪声干扰(e)的实际信号,测量模型可以表示为[8]
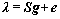
2 基于稀疏正则化的重构算法
2.1 稀疏表达
基于1范数的ECT重构问题可描述为
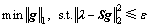
利用拉格朗日乘子法,得到
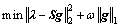
对此,DAUBECHIES等[16]提出了相应的软阈值函数以实现稀疏性:
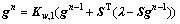
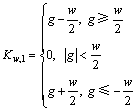
其中:w为正则化参数。
2.2 步长
Landweber迭代过程可描述为[9]
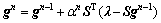
其中:步长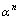 的选择是一个重要问题,合适的步长可以加速收敛,减少计算时间。LIU等[16]提出了一种计算最佳步长的方法,即下式
的选择是一个重要问题,合适的步长可以加速收敛,减少计算时间。LIU等[16]提出了一种计算最佳步长的方法,即下式
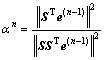
其中: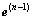 为测量电容与计算电容之间的误差,计算公式为[21]
为测量电容与计算电容之间的误差,计算公式为[21]
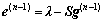
本文采用式计算步长。
2.3 软阈值函数
YE等[20]提到,在外置电极的ECT传感器中,2类连续相分布不同的流型在用Landweber算法进行图像重构时,连续相为高介电常数的分布随迭代步数的增加高介电常数区域增大,连续相为低介电常数的分布则随着迭代步数的增加呈现相反的变化。据此,本部分首先对内外置电极的ECT传感器进行类似的研究,即对2类连续相分布不同的流型进行模拟。
图1所示为本文进行模拟所使用的2种流型图。2种流型连续相分布存在差异,D1分布中连续相的介电常数为3.5,离散相介电常数为1;D2分布中连续相的介电常数为1,离散相介电常数为3.5。
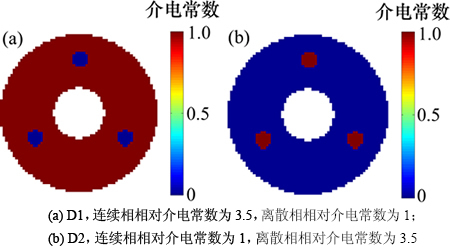
图1 真实介电常数分布
Fig. 1 True permittivity distribution for simulation
图2所示为随着迭代步数的增加,重构图像中介质分布的变化趋势。此处算法采用Landweber迭代算法。由图2可以看出:2种分布下连续相随着迭代步数的增加其变化趋势是不同的。D1中连续相为高介电常数分布,随着迭代步数增加,高介电常数区域增大,而D2与之相反。结论与外置电极的ECT传感器相同。据此,根据YE等[20]的结论,软阈值函数可以根据连续相分布不同而分为2类。对于连续相为低介电常数的分布,软阈值函数定义为
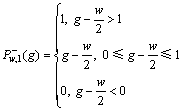
对于连续相为高介电常数的分布,软阈值函数定义为
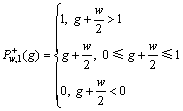

图2 在Landweber迭代算法下,D1和D2分布随着迭代步数增加时的重构图像
Fig. 2 Images reconstructed for D1 and D2 with increase of number of iterations with Landweber iterative algorithm
其中:w为正则化参数。
2.4 算法总结
步骤1) 计算敏感场S。
步骤2) 输入S,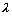 和
和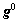 。对于
。对于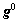 ,本文中采用下式计算[22]:
,本文中采用下式计算[22]:
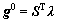 (13)
(13)
步骤3) 利用式计算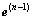 [21]。
[21]。
步骤4) 利用式计算步长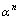 [21]。
[21]。
步骤5) 利用下式计算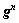 :
:
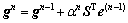 (14)
(14)
步骤6) 根据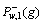 或
或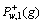 调整
调整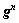 的元素值。
的元素值。
步骤7) 若满足收敛准则,则输出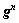 ,否则返回步骤3。
,否则返回步骤3。
3 数值模拟
3.1 模拟条件简介
本文采用一个外置12电极内置4电极的ECT模型进行模拟,如图3所示。软件采用COMSOL Multiphysics和Matlab。对于正问题,在COMSOL中,成像区域被划分为‘fine’程度的网格。对于逆问题,成像区域被划分为64×64个网格,环形区域有效像素为2 944个。
敏感场矩阵在图像重构过程中起着非常重要的作用。对于内外置电极的ECT传感器,其敏感场计算方法与传统ECT类似,仍采用式。得到结果之后,对敏感场矩阵进行归一化处理。图4所示为本文的归一化平均敏感场分布,即像素为归一化敏感场矩阵中每一列的平均值。
根据YE等[20]的研究,相关系数可以更好地反映重构图像的质量。因此,本文选择相关系数作为图像质量的评价标准,其表达式为[9]
 (15)
(15)
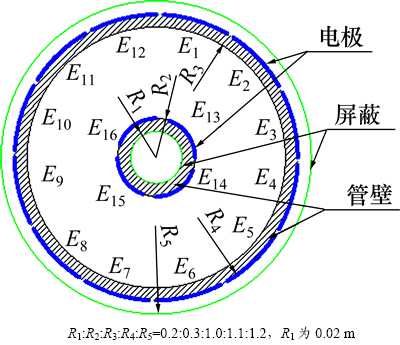
图3 内外置电极ECT传感器简图
Fig. 3 Diagram of IEE ECT sensor
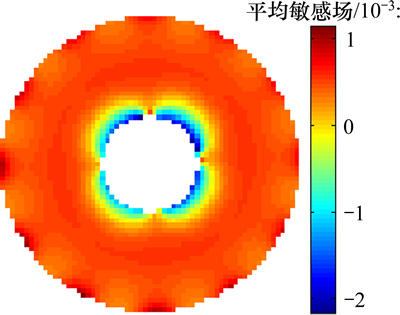
图4 归一化平均敏感场分布
Fig. 4 Normalized sensitivity distribution
其中: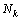 为成像区域的像素数,本文中为2 944个;
为成像区域的像素数,本文中为2 944个;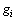 和
和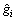 分别为真实分布图像和重构图像在i点的像素;
分别为真实分布图像和重构图像在i点的像素; 和
和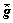 分别为真实分布图像和重构图像像素的平均值;r为相关系数。
分别为真实分布图像和重构图像像素的平均值;r为相关系数。
3.2 模拟结果
本部分利用图1中D1和D2分布来进行数值模拟研究。图5所示为基于软阈值的稀疏正则化重构算法所得到的图像。当正则化参数为0时,此算法即为Landweber迭代算法。由图5可以看出:在一定范围内,随迭代步数增加,图像质量增加;随着正则化参数增加,图像质量增加。另外,随着正则化参数增加,介电常数不同的2种物质其边界也更加明显。据此可以得出,具有合适正则化参数的稀疏正则化重构算法可以提高图像质量。对于D2,当正则化参数为0.04,迭代步数大于10步时,图像已经不能反映原来的流型。这说明在一定范围内的正则化参数可以提高图像质量,超出这个范围则会降低图像质量。
对于D1和D2的图像重构,图6所示为其相关系数与正则化参数(w)及迭代步数的关系。总体来看,相关系数随着正则化参数的增加而增加,随着迭代步数的增加而增加。但是,当正则化参数超过某一值后,相关系数会减小。对于D1,迭代步数为30时,正则化参数由0.07增加到0.08后,相关系数减小;迭代步数为40时,正则化参数大于0.06后,相关系数减小。对于D2,在所有4种迭代步数之下,正则化参数由0.03增加到0.04后,相关系数减小。
通过对重构图像的定量分析可以得到,与Landweber迭代算法相比,1个合适的正则化参数可以提高图像质量;此外还可以得到,合适的正则化参数可以减少迭代步数,提高成像速度。
3.3 经验正则化参数分析
YE等[20]研究表明:此算法中的经验正则化参数可以根据LBP算法所计算的最大介电常数相关的经验值来确定。图7所示为用经验正则化参数对D1和D2分布所重构的图像。由图7可以看出:基于经验正则化参数的稀疏重构算法所重构出的图像质量要高于Landweber迭代算法;表1和表2所示分别为D1分布下,基于不同经验正则化参数所得图像的相关系数和D2分布下,基于不同经验正则化参数所得图像的相关系数。由表1和2可以看出:针对本文所分析的分布,在一定范围内,重构图像的相关系数随经验正则化参数的增加而增加。但是,对于D1分布,当正则化参数为0.7倍的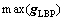 时,图像质量明显下降;对于D2分布,当正则化参数为4倍的
时,图像质量明显下降;对于D2分布,当正则化参数为4倍的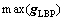 时,图像质量也出现下降的情况。这说明,若经验正则化参数选的过大,图像质量会下降。
时,图像质量也出现下降的情况。这说明,若经验正则化参数选的过大,图像质量会下降。
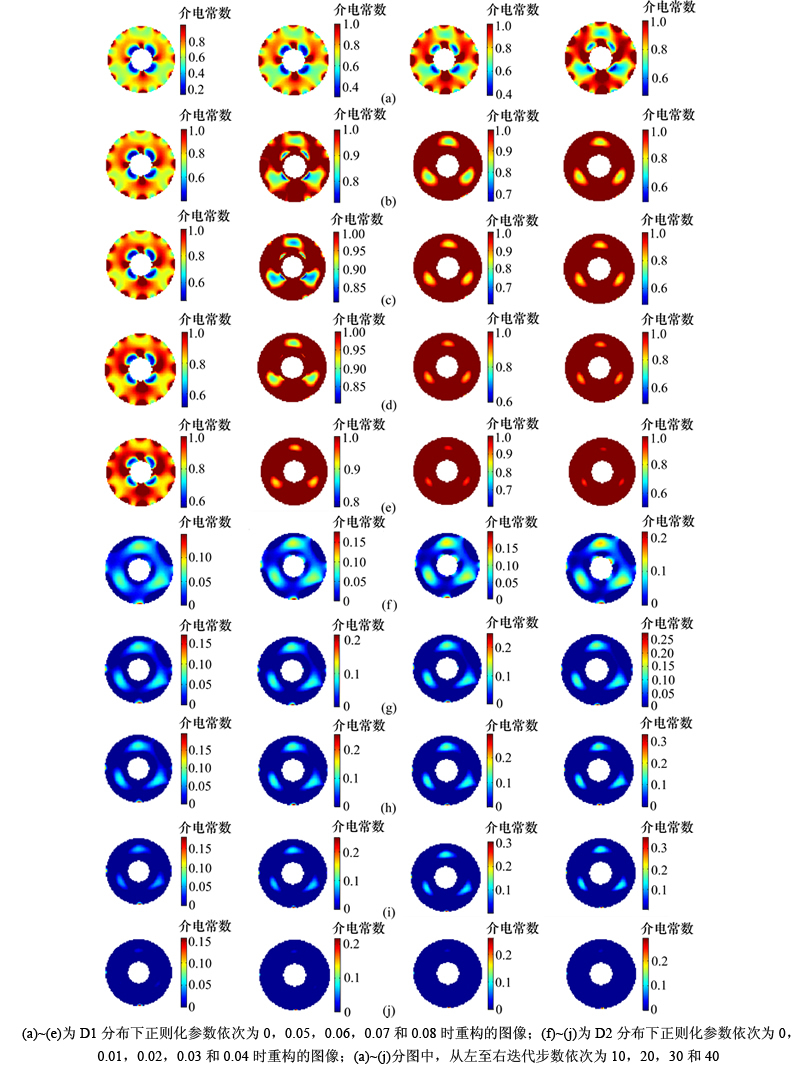
图5 利用Landweber迭代和基于软阈值的稀疏正则化算法得到的重构图像
Fig. 5 Images reconstructed by Landweber iterative algorithm and the sparse regularization algorithm
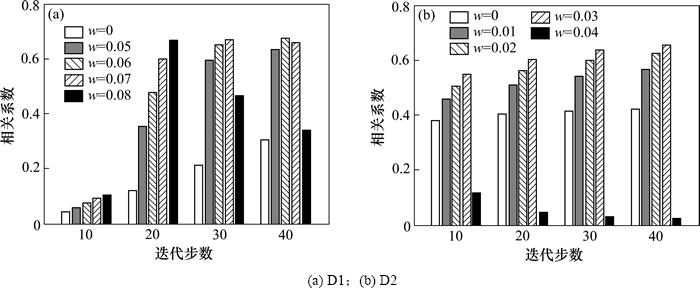
图6 相关系数与正则化参数和迭代步数的关系
Fig. 6 Correlation coefficient with different regularization parameters and different number of iterations
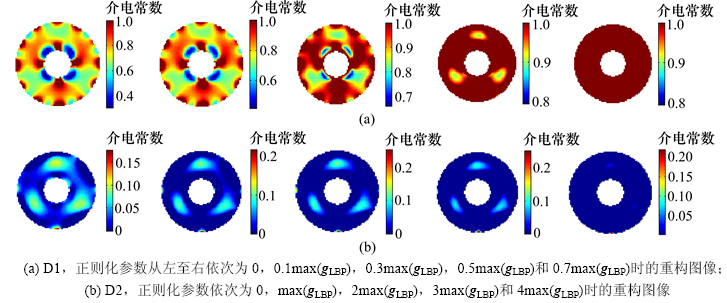
图7 基于经验正则化参数的稀疏正则化算法所重构的图像(迭代步数为20)
Fig. 7 Images reconstructed by sparse regularization algorithm with empirical regularization parameters (The number of iterations is 20)
表1 D1分布下,基于不同经验正则化参数所得图像的相关系数
Table 1 Correlation coefficient for D1 with sparse regularization algorithm with empirical regularization parameters

表2 D2分布下,基于不同经验正则化参数所得图像的相关系数
Table 2 Correlation coefficient for D2 with sparse regularization algorithm with empirical regularization parameters

4 实验研究
4.1 实验设备
本文实验所采用的ECT系统为16测量通路的AC-ECT系统,激励信号的频率为100 kHz,激励电压振幅为18 V。ECT传感器采用外置12电极、内置4电极的布置方式。
图8所示为本文实验所采用的真实介电常数分布。高介电常数区域采用沙子,相对介电常数为2.5;低介电常数区域为空气,相对介电常数为1。
4.2 实验结果分析
图9所示为实验所得到的结果。迭代步数选择1,5和10步,正则化参数选择0,0.02,0.04和0.06。正则化参数为0时,算法转化为Landweber迭代算法。由图9可以得到:在一定范围内,随着迭代步数增加,图像质量增加;在一定范围内,随着正则化参数增加,图像质量增加。相比Landweber迭代算法,在基于软阈值的稀疏正则化重构算法下,不同材料的边界更加明显,图像质量也更高。

图8 实验所采用的真实介电常数分布
Fig. 8 True distribution of relative permittivity used in experiment
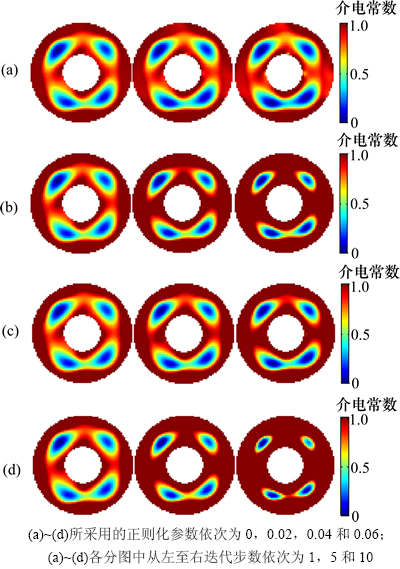
图9 采用Landweber算法和基于软阈值的稀疏正则化算法对内外置电极ECT重构所得实验结果
Fig. 9 Images reconstructed by Landweber iterative algorithm and sparse regularization algorithm using experimental data
此外,当正则化参数为0.06,迭代步数为10步时,图像已经发生扭曲,说明正则化参数应限制在一定范围内,否则会降低图像质量。实验结果与仿真结果吻合较好。
5 结论
1) 在内外置电极的ECT传感器中,基于软阈值的稀疏正则化重构算法相比Landweber迭代算法可以明显减少迭代步数,提高图像质量。
2) 与其他迭代算法类似,本文所采用的算法也需要在一定范围内设置正则化参数以保证图像质量。
3) 本文对经验正则化参数进行了分析。基于LBP重构图像最大介电常数的经验正则化参数设定方法可以便于该算法的在线使用。
参考文献:
[1] YANG Wuqiang. Design of electrical capacitance tomography sensors[J]. Meas Sci Technol, 2010, 21(4): 042001.
[2] 王化祥, 唐磊, 崔自强. 油/气两相流高速电容层析成像可视化系统[J]. 中国电机工程学报, 2009, 29(5): 61-65.
WANG Huaxiang, TANG Lei, CUI Ziqiang. A high-speed ECT visualization system for oil/gas two-phase flow[J]. Proceedings of the CSEE, 2009, 29(5): 61-65.
[3] 陈琪, 刘石. 多孔介质内燃烧的电容层析成像可视化测量及数值分析[J]. 中国电机工程学报, 2007, 27(29): 63-67.
CHEN Qi, LIU Shi. Electrical capacitance tomography visualization and numerical analysis of combustion in porous media[J]. Proceedings of the CSEE, 2007, 27(29): 63-67.
[4] 孙猛, 刘石, 雷兢, 等. 利用电容层析成像法测量气力输送中的煤粉流量[J]. 动力工程, 2008, 28(3): 411-414.
SUN Meng, LIU Shi, LEI Jing, et al. Measurement of flow rate of pulverized coal in pneumatic conveying using electrical capacitance tomography[J]. Journal of Power Engineering, 2008, 28(3): 411-414.
[5] 杨道业, 周宾, 许传龙, 等. 电容层析成像在高压浓相煤粉气力输送中的应用[J]. 仪器仪表学报, 2007, 28(11): 1987-1993.
YANG Daoye, ZHOU Bin, XU Chuanlong, et al. Application of electrical capacitance tomography in dense-phase pneumatic conveying of pulverized coal under high pressure[J]. Chinese Journal of Scientific Instrument, 2007, 28(11): 1987-1993.
[6] 王海刚, 赵国荣, 邱桂芝. 循环流化床多旋风分离器入口电容层析成像测量[J]. 工程热物理学报, 2014, 35(1): 109-113.
WANG Haigang, ZHAO Guorong, QIU Guizhi. Investigation the solid phase distribution in the inlet of multi-cyclone of a circulating fluidised bed by electrical capacitance tomography[J]. Journal of Engineering Thermalphysics, 2014, 35(1): 109-113.
[7] YE Jiamin, LI Yi, WANG Haigang, et al. Concentric-annulus electrical capacitance tomography sensors[J]. Meas Sci Technol, 2013, 24(9): 095403.
[8] XIE Chenggang, HUANG Songming, HOYLE B S, et al. Electrical capacitance tomography for flow imaging: system model for development of image reconstruction algorithms and design of primary sensors[J]. IEE Proc G, 1992, 139(1): 89-98.
[9] YANG Wuqiang, PENG Lihui. Image reconstruction algorithms for electrical capacitance tomography[J]. Meas Sci Technol, 2003, 14(1): R1-R13.
[10] PENG Lihui, MERKUS H, SCARLETT B. Using regularization methods for image reconstruction of electrical capacitance tomography[J]. Part Part Syst Charact, 2000, 17(3): 96-104.
[11] LEI Jing, LIU Shi. Dynamic inversion approach for electrical capacitance tomography[J]. IEEE Transactions on Instrumentation and Measurement, 2013, 62(11): 3035-3049.
[12] DONOHO D L. For most large underdetermined systems of linear equations the minimal 1-norm solution is also the sparsest solution[J]. Commun Pure Appl Math, 2006, 59(6): 797-829.
[13] DONOHO D L, JOHNSTONE I M. Ideal spatial adaptation via wavelet shrinkage[J]. Biometrika, 1994, 81(3): 425-455.
[14] DONOHO D L. Orthonormal ridgelets and linear singularities[J]. SIAMJ Math Anal, 2000, 31(5): 1062-1099.
[15] CANDES E J, DONOHO D L. Recovering edges in ill-posed inverse problems: optimality of curvelet frames[J]. Ann Statist, 2002, 30(3):784-842.
[16] DAUBECHIES I, DEFRISE M, De MOL C. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint[J]. Commun Pure Appl Math, 2004, 57(11): 1413-1457.
[17] YE Jiamin, WANG Haigang, YANG Wuqiang. Image reconstruction for electrical capacitance tomography based on sparse representation[J]. Instrumentation and Measurement, 2014, 64(1): 89-102.
[18] JIN Bangti, KHAN T, MAASS P. A reconstruction algorithm for electrical impedance tomography based on sparsity regularization[J]. International Journal for Numerical Methods in Engineering, 2012, 89(3): 337-353.
[19] DONG Xiangyuan, YE Zhuoyi, SOLEIMANI M. Image reconstruction for electrical capacitance tomography by using soft-thresholding iteration method with adaptive regularization parameter[J]. Meas Sci Technol, 2013, 24(8): 085402.
[20] YE Jiamin, WANG Haigang, YANG Wuqiang. A sparsity reconstruction algorithm for electrical capacitance tomography based on modified Landweber iteration[J]. Meas Sci Technol, 2014, 25(11): 115402.
[21] LIU Shi, FU Lei, YANG Wuqiang. Optimization of an iterative image reconstruction algorithm for electrical capacitance tomography[J]. Meas Sci Technol, 1999, 10(7): L37-L39.
[22] YANG Wuqiang, SPINK D M, YORK T A, et al. An image-reconstruction algorithm based on Landweber's iteration method for electrical-capacitance tomography[J]. Meas Sci Technol, 1999, 10(11): 1065-1069.
(编辑 陈爱华)
收稿日期:2015-07-20;修回日期:2015-09-26
基金项目(Foundation item):国家自然科学基金资助项目(61374018, 61320106004) (Projects(61374018, 61320106004) supported by the National Natural Science Foundation of China)
通信作者:叶佳敏,博士,副研究员,从事多相流测量研究;E-mail: yejiamin@iet.cn